トリニティコンピューティング
私は大学の学生向けにコンピュータアーキテクチャに関する講義コースを準備していますが、小さな実践的なトレーニングとして、学生に三元論理の原始プログラマブルコンピュータを構築することをお勧めします。 具体的には、この記事では、構築に使用される基本モジュール、つまり3進マルチプレクサーについて説明します。 このテキストでは、最も単純な加算器(およびそのハードウェアでの実装)を超えることはありません。テキストはすでにかなり飽和しています。 以降の記事では、この曲線が私をどこへ導くのかをゆっくりとお話しします。冒険の最初の段階にいるからです。
1つのトリットが-1、0、1の3つの値のいずれかを表すことができるバランスの取れた3進法を選択しました 。詳細については、 こちらをご覧ください 。
「なぜ?!」というカテゴリの質問については、事前に「できるから」と答えます。

建築材料:三元マルチプレクサ
論理レベル
基本的な建築材料は、三元マルチプレクサです。 論理的には、これは5つのピンに関するものです:それらの1つ(sel)は3進セレクター信号を受信し、それに応じて、3つの入力信号inN、inOまたはinPの1つがマルチプレクサーの出力(out)に供給されます。
ダイアグラムでは、通常、次のように何らかの形で描かれます。

デマルチプレクサは同様に機能します。セレクタに応じて、1つの入力が3つの出力の1つに閉じられます。 私が使用するハードウェアには双方向キーがあるため、同時にマルチプレクサとデマルチプレクサの両方になります(ただし、逆多重化の可能性はまだ使用していません)。
鉄の実現
ハードウェアの設計はAlexander Shabarshinに属し、正直に言って完全に口wを吹いた。 私がした唯一のことは、表面実装用の鉄片を広げることでした これらの超小型回路は、出力超小型回路よりも大幅に安価です。中国では、1個50セントで購入できます。

この設計に出くわす前に(ところで、 Alexanderフォーラムには3進コンピューティングとグランドに関する多くの情報があります)、私はcd4016とcd4007から庭をフェンスしようとしましたが、うまくいきましたが、非常に面倒で不便でした。 dg403キーを使用すると、3ビットシステムを2ビットバイナリでエンコードするような冗長性のない実際の3要素が得られます。
ちなみに、多くの理論家とは異なり、アレキサンダーはさらに進んで、三元論理で動作する自分のマイクロサーキットを開発し、注文しました。

1つのTRIMUXマルチプレクサーを作成するために、アレキサンダーは2つのdg403キー超小型回路を使用しました.1つは-5Vと0Vの間でロジックに電力が供給され、もう1つは0Vと5Vの間で電力が供給され、-5、0および5Vの3つの電圧レベルで表される3値信号を処理できます。 しかし、これにより足の半分が自由になるため、2つの3進マルチプレクサーが2つのdg403マイクロ回路にちょうど収まります。

使い方は? 単一引数関数
マルチプレクサの対応する入力に-1、0、1を適用することで取得できる簡単な恒等関数をスキップしましょう。
まず、入力信号Aに1を追加しましょう(もちろん、リング-1,0,1内):
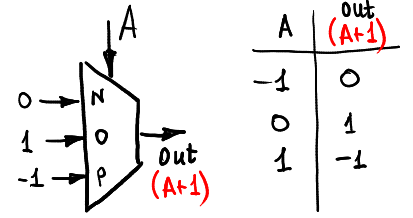
したがって、単位を減算できます。
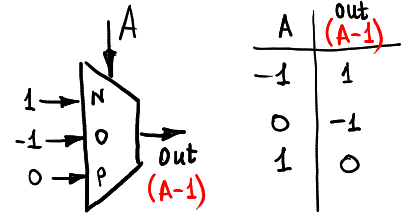
これは、単一の引数max(A、0)の関数を計算する方法です。
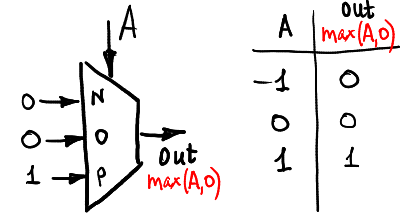
そして、ここに最小(A、0):

2つの引数の関数:半加算器
A + B
したがって、1つの引数の関数を計算するには、1つのマルチプレクサで十分です。 2つの引数の関数を計算するには、3つまたは4つのマルチプレクサを使用する必要があります。 たとえば、2つの3値信号AとBの合計を計算する場合(以前と同様に、リング-1,0,1内)、次のスキームを使用できます。
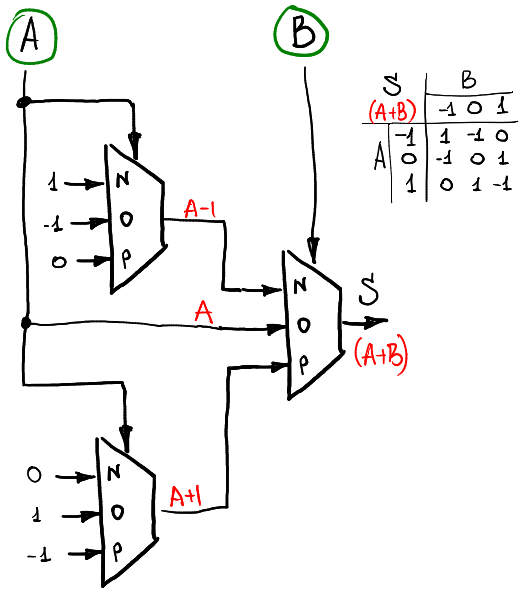
マルチプレクサーの最初のレベルは信号Aからの1つの引数の関数を考慮し、2番目のレベルは信号レベルBに応じてそれらを使用します。
コンセンサス
2つの3値信号のコンセンサス関数を計算したい場合(A = B = -1の場合は-1、A = B = 1の場合は1、それ以外の場合はゼロ)、これは次のように実行できます。

鉄の実現
そのため、 半加算器を作成しました。 2つの入力AとBに応じて、A + B = S + 3 * Cとして計算できる2つの出力SとCを生成します。
テストしてみましょう! 赤いダイオード= -1、オフ= 0、緑=1。したがって、この写真は、S = -1、C = 1、つまり1 + 1 = -1 + 3 * 1:であることを示しています。

このプレートは、半加算器の9つの可能な状態すべてを提供し、各セルはSとCの対応する値を提供します。セル内のリンクによって鉄の写真に対応します。
| S c | B | |||
| -1 | 0 | 1 | ||
| A | -1 | 1、-1 | -1.0 | 0,0 |
| 0 | -1.0 | 0,0 | 1,0 | |
| 1 | 0,0 | 1,0 | -1.1 | |
3つの引数の関数:全加算器
全加算器は、半加算器として2つではなく、入力として3つの引数を取る必要があります。 3番目の引数は、低次からの転送です。 したがって、3つの入力A、B、およびCinから、A + B + Cin = S + 3 * Coutの法則に従って2つの出力SおよびCoutをカウントする必要があります。
3つのトリットの合計
3つの引数の関数の場合、考え方は2つの関数の場合とまったく同じです。後続の計算には階層化されたデータ準備を使用します。 つまり、マルチプレクサの最初の層はA入力のみを受け入れ、2番目はBだけを受け入れ、最後のマルチプレクサはCinだけを受け入れます。
これはSの計算スキームのように見えるかもしれません:
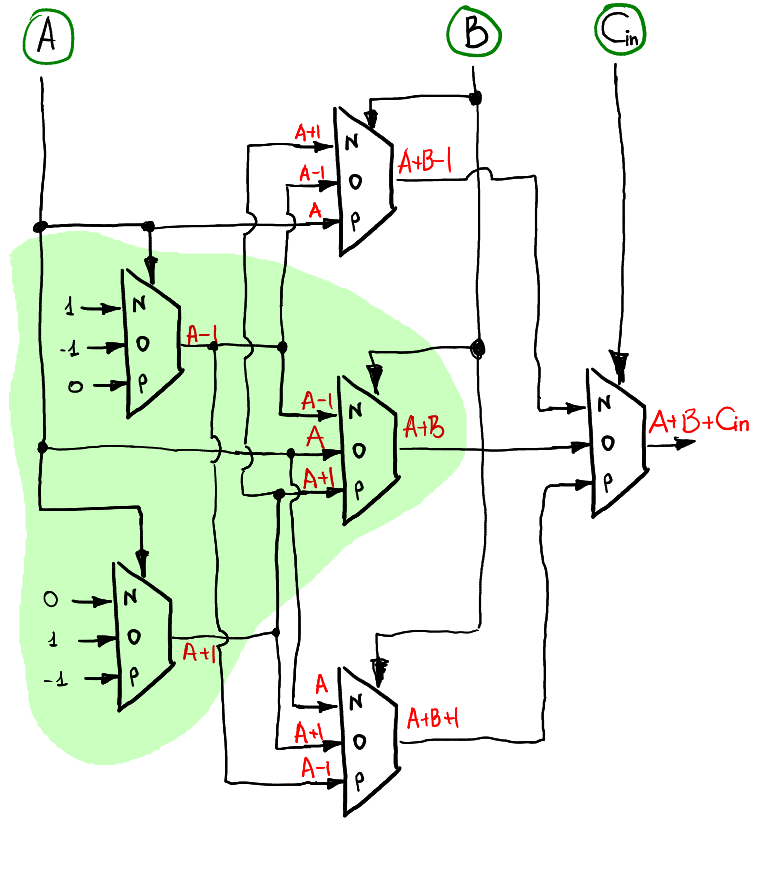
Cin = 0の場合、実際には半加算器の操作を繰り返す必要があることに注意してください。 半加算器が全加算器回路に含まれることは論理的です(緑色で強調表示)。
結果のオーバーフロー
オーバーフロートリットは完全に類似していると見なされ、まったく同じ方法で、回路に半加算オーバーフロートリット計算回路が含まれています。

鉄の実現
今回はブレッドボードのワイヤーを突くにはあまりにも面倒だったので、すぐにボードを広げました:

そして、ゲティナカの株から何世紀も昔の塵を吹き飛ばしました:

全加算器の27の可能な状態がすべてあります。中央のテーブル( Cin = 0の場合 )が半加算器のテーブルを繰り返すことに注意してください。
| Cin = -1 | B | |||
| -1 | 0 | 1 | ||
| A | -1 | 0 -1 | 1、-1 | -1.0 |
| 0 | 1、-1 | -1.0 | 0,0 | |
| 1 | -1.0 | 0,0 | 1,0 | |
| Cin = 0 | B | |||
| -1 | 0 | 1 | ||
| A | -1 | 1、-1 | -1.0 | 0,0 |
| 0 | -1.0 | 0,0 | 1,0 | |
| 1 | 0,0 | 1,0 | -1.1 | |
| Cin = 1 | B | |||
| -1 | 0 | 1 | ||
| A | -1 | -1.0 | 0,0 | 1,0 |
| 0 | 0,0 | 1,0 | -1.1 | |
| 1 | 1,0 | -1.1 | 0.1 | |
全加算器の良い点は、必要なビット深度が得られるまで、そのようなボードをサンドイッチに組み立てられることです。
2桁のサンドイッチを次に示します。

これは、彼が-4 + 2の例を解決する方法です(左のボードが最下位ビットです):

実際、もちろん、最年少のカテゴリでは全加算器は必要ありません。最下位の放電の加算器の入力に転送する必要がないため、半加算器で十分です。 しかし、私はすでにブレッドボード上の半加算器を分解し、それを回収するのが面倒です:)
おわりに
この記事では、3値コンピューティングのベースを構築する方法と方法について簡単に説明しました。 将来のリリースでは、カウンタ、メモリ、ALUなどを待ちます。 お楽しみに!