スプライン補間の理論的基礎またはIQテストに解決策がない理由

楽しい時間を！



最初の記事を書いてからかなりの時間が経過し、 2番目の記事を思いついた瞬間からほぼ1年が経ちました。 多くの状況（主に怠inessと忘却）のために、このアイデアは以前に実現したことはありませんでしたが、今私は集まって、このすべての資料を書き、あなたの注意にそれを提示する準備ができています。



簡単な紹介から始めましょう。 4回目の学生として、当時、学部課程で、私はコース「コンピューターグラフィックス」を学びました。 さまざまな興味深い（そしてそうではない）タスクがありましたが、私の魂に直接影響を与えたものが1つありました。それは、間隔の終わりに与えられた1次導関数を使用した3次スプラインによる補間です。 ユーザーは一次導関数の値を設定する必要があり、プログラムは補間曲線を読み取って表示する必要がありました。 タスクの特殊性と主な難しさは、スプライン補間の古典的な定式化のように、指定されているのは一次導関数であり、二次導関数ではないという事実にあります。

どうやってそれを解決したのか、そして最終的に何になったのかを、この記事で説明します。 そして、はい、タスクの説明に従ってその意味、複雑さを理解していなくても心配しないでください、私はこれもすべて明らかにしようとします。 行きましょう。



ああ、ちょっと待って。 以下に2つの数字を示します。

a）2、4、6、8 、?

b）1、3 、? 7、9



質問の代わりに何の数字を立てるべきか、そしてその理由は？ あなたの答えは本当に確かですか？

補間

補間、補間（ラテン語inter-polisから-「平滑化、更新、更新、変換」）は、計算数学において、既知の値の利用可能な離散セットから量の中間値を見つける方法です。 （c）ウィキペディア

例で説明します。 条件付きで、既知の値のいくつかによって特定のパラメーターの「分布則」（一般的には数学の別の領域からの用語であるため、引用符で囲む）を見つける必要があるときに問題があります。 ほとんどの場合、時間の経過に伴うパラメーターの変化について話します：動体の座標、物体の温度、通貨の変動など。 さらに、状況によっては、このパラメーターを継続的に監視する機会がなかったため、特定の時点でのみその値を認識できました。 この場合、ソースデータはフォーム値（時間）のポイントのセットであり、タスクの目標は、これらのポイントを通過し、このパラメーターの変化を継続的に記述する曲線を復元することです。



関連するパラメータの継続的な監視が不可能であることは、通常、何らかの技術的制限であることを理解されたい。 技術の発展により、そのような状況はますます少なくなっています。 そのような計画の現代のタスクのうち、たとえばローバーの移動の軌跡があります。 継続的なコミュニケーションセッションを維持することはまだ不可能ですが（現時点では）、その動きを制御し、美しい軌跡を描きたいと思います。 特定の座標は、接続がまだ確立されている時点でのみ見つけることができ、このように時々取得したポイントから軌跡全体を復元する必要があることがわかります。

補間の別のアプリケーション。 最新のテレビの中には、画像のリフレッシュレートが1000 Hz以上の画像を表示するものがあります（ただし、これらはまだとんでもない値です）。 ほとんどのテレビはこれを行う方法を知りませんが、非常に多くのテレビでも100 Hzの周波数で画像を表示します。この値はすでにかなり古典的です。 そして、ウィキペディアを信じるなら、映画館では「1秒あたり24フレームの頻度が世界標準です」。 元のビデオストリームの1秒あたり24フレームを結果の1秒あたり100フレームに変換するために、TVは補間を使用します。 すなわち、「2つの隣接するフレーム1と2を取得し、それらの差を計算し、それらの2つの初期フレーム間で押し込む必要がある3つの追加フレームを形成する」スタイルのアルゴリズム->フレーム1、1_1、1_2、1_3、2が取得されます



さらに議論するために、より簡単な例を見てみましょう。 たとえば、6年生の地理学の研究室での作業を想像してみてください（ところで、私はかつて実際に1つ持っていました）。 3時間ごとに気温を測定し、データを記録してから、温度の変化と時間の関係を教師に伝える必要があります。 測定の結果に従って、そのようなプレートを得たと仮定します（データはランダムに発明されたものであり、信頼性を装ってはいません）：











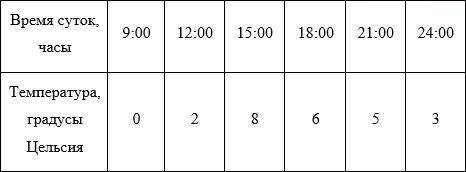
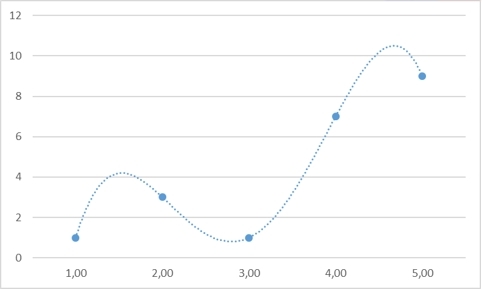
チャートにデータを表示します。











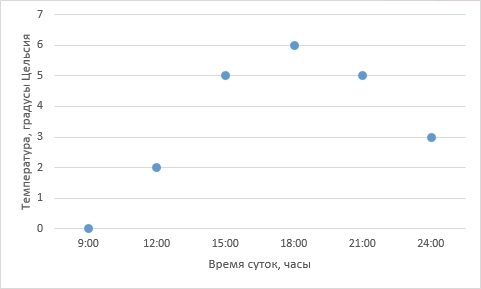
実際、データは記録され、グラフに反映されます。 補間の問題に近づきました-利用可能な点から滑らかな曲線を復元する方法は？

条件数と補間多項式の次数

一般に、与えられたすべてのポイントを接続するような関数が存在することを保証できますか？



はい、そのような関数は存在することが保証されており、さらに、そのような関数は無限にあります。 ポイントの任意のセットに対して、それらを通過する必要な関数をいくつでも作成することができます。 また、2つのポイントをさまざまな方法で接続する方法の例をいくつか示します。























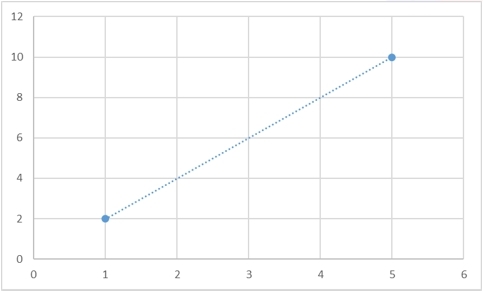
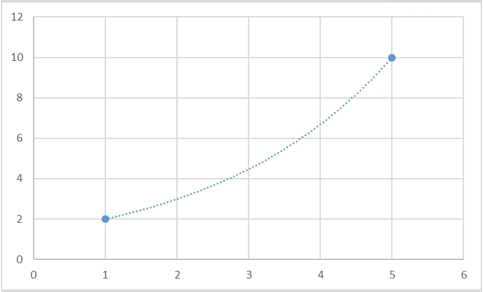
ただし、補間曲線を一意に設定する方法があります。 最も古典的な場合、多項式は補間曲線として使用されます。



$$$P_n（x）= a_nx ^ n + a_ {n-1} x ^ {n-1} + ... + a_1x + a_0$



使用可能な点を介してこのような多項式を独自の方法で描画するには、多項式の次数が条件の数より1少ないことが必要で十分です（このセクションの最後でこの定式化に戻るため、この単語を特別に強調しました）。 今のところ、簡単にするために、条件はポイントの座標になります。 人間の言語では、2点を介して直線（1次の多項式）、3点を介して-放物線（2次の多項式）などを明確に描くことができます。



温度の問題に戻り、6つの点を特定しました。つまり、多項式を独自の方法で実行するには、5次でなければなりません。











補間多項式は次のようになります。



$$ $インライン$-\ frac {x ^ 5} {14580} + \ frac {13x ^ 4} {1944}-\ frac {41x ^ 3} {162} + \ frac {983x ^ 2} {216}-\ frac {2273x} {60} + 117 $インライン$



そして今、重要な発言をし、 「条件」が意味することを明確にしなければなりません。 多項式は、通過する点の座標だけでなく、条件はこの多項式の任意のパラメーターに設定できます。 最も単純な場合、これらは実際にはポイントの座標です。 しかし、条件として、たとえば、ある時点でこの多項式の一次導関数をとることができます。 二次導関数。 三次導関数。 一般に、この多項式が存在する任意の点での可能な微分。 例で説明します。

先ほど言ったように、直線は次の2点で一意に定義できます。











一方、同じ直線は、1つの点の座標と水平線に対するアルファの傾斜角によって決定できます。











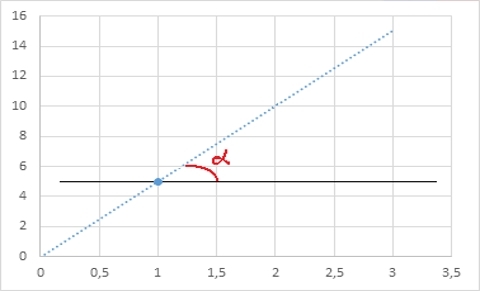
次数の高い多項式は、より複雑な条件（2次導関数、3次導関数など）を使用することもでき、このような各パラメーターは、この多項式を一意に決定する条件の数の一般的な説明になります。 根拠がないようにするために、別の例を示します。



3つの条件が与えられます。



$$$y（0）= 1、y '（0）= 1、y' '（0）= 2$



3つの条件があります。これは、2次の多項式を取得することを意味します。



$$$y（x）= ax ^ 2 + bx + c$



代用 $$$x = 0 \ to y（x = 0）= c \ to c = 1$



一次導関数を考慮し、 $$$y '（x）= 2ax + b \ to [x = 0] \ to y'（x = 0）= b \ to b = 1$



二次導関数を数えて $$$y ''（x）= 2a \ to [x = 0] \ to y ''（x = 0）= 2a \ to a = 1$



ここから、多項式は次のようになります。



$$$y（x）= x ^ 2 + x + 1$

3次スプライン補間

ここで、静かに、私たちは私の仕事を始めています。 多項式補間は、補間の唯一の可能な方法ではありません。 他のすべての方法の中で、3次スプラインによる補間の方法があります。



スプライン補間と多項式による補間の考え方の根本的な違いは、1つの多項式があり、スプラインが複数の多項式で構成されていることです。つまり、その数は補間する間隔の数に等しくなります。 6つのポイントがある気温の例では、5つの間隔があります。したがって、それぞれ独自の間隔で5つの多項式があります。



これらの多項式はそれぞれ3次の多項式です（厳密には、次数は3次より高くなりません。ある間隔で補間曲線が2次放物線または線形関数になることもありますが、一般的な場合は3次の多項式です） 。 上記の式を書くと、すべてのポイントが特定の曲線で接続されます $$$S = \ {S_1、S_2、S_3、S_4、S_5 \}$ 誰もが $$$S_i$ 3次の多項式、つまり：



$$$S_i（x）= ax ^ 3 + bx ^ 2 + cx + d$



前の段落で述べたことに戻ると、3次の1つの多項式を一意に指定するには、4つの条件が必要です。 この問題では、5つの多項式があります。つまり、それらすべてを求めるには、合計で5∙4 = 20の条件が必要です。 そして、ここで彼らが得る方法です：



1）最初の多項式は最初と2番目のポイントで定義されます-これらは2つの条件です。 2番目の多項式は、2番目と3番目のポイントで定義されます-さらに2つの条件。 3番目の多項式、4番目、5番目-それぞれが2点で定義され、合計で10個の条件が与えられます。



2）セットからの各中間点（およびこれらは時間12：00、15：00、18：00、21：00の4点）について、左右の多項式の1次および2次導関数が一致する必要があるという条件を満たす必要があります。 正式に：



$$$S_ {1} ^ {'}（x = 12：00）= S_ {2} ^ {'}（x = 12：00）$



$$$S_ {1} ^ {''}（x = 12：00）= S_ {2} ^ {''}（x = 12：00）$



$$$など$



中間点のそれぞれに対するこのような2つの条件は、さらに8つの条件を与えます。 私たちは平等の事実だけを問うことを付け加えるべきであり、彼らがそうすることで取る具体的な重要性は完全に異なるタスクであり、それは非常に難しいと考えられています。



3）まだ定義されていない2つの条件が残っています。 これらは、いわゆる「境界条件」であり、どのスプラインが正確に決定されるかによって決まります。 通常、間隔の終わりの2次導関数は0に設定されます。



$$$S_ {1} ^ {''}（x = 9:00）= 0$



$$$S_ {5} ^ {''}（x = 21：00）= 0$



これを行うと、いわゆる「自然なスプライン」が得られます。 このようなスプラインを計算するために、膨大な数のライブラリがすでに作成されており、いずれかを使用します。

私のタスクと問題の古典的な声明の違い、タスクとソリューション自体に対する私の考え

そして今、私たちは私の仕事の状態になりました。 教師は、最初の派生物を尋ねるべきタスクを思いついた $$$S_ {1} ^ {'}（x_1）= k_1$ そして $$$S_ {n-1} ^ {'}（x_n）= k_2$ 間隔の左端と右端で、プログラムは補間曲線を読み取る必要があります。 そして、そのような要件については、既製のアルゴリズムは見つかりませんでした...

もちろん、課題を聞いてから合格するまでの「創造的な」道筋全体については説明しません。 アイデアそのものを伝え、その実装を示します。



タスクの複雑さは、間隔の終わりに最初の導関数を設定することです。はい、このスプラインを定義します。 理論的に。 しかし、実際に計算するのはかなり複雑で完全に非自明なタスクです（Wikiで自然なスプラインを見つけるためのコード（ en.wikipedia.org/wiki/Cubic_splineを見て、少なくともそれを理解しようとする人）。 もちろん、私は絶対にマタンを掘り下げ、必要な式を推測しようと多くの時間を費やしたくありませんでした。 もっとシンプルでエレガントなソリューションが欲しかった。 そして私は彼を見つけました。

スプラインを考慮して、最初の間隔を取ります。 この間隔では、3つの条件が既に設定されています。



$$$S_1（x_1）= y_1$



$$$S_1（x_2）= y_2$



$$$S_ {1} ^ {'}（x_1）= k_1$ -ユーザーが設定



この区間で3次多項式を一意に指定するには、もう1つの条件が必要です。 しかし、私たちはそれを思いつくことができます！ 2次導関数を取り、それを等しく設定します（例：0）：



$$$S_ {1} ^ {''}（x_1）= 0$ -根拠のない仮定



したがって、これらの4つの条件を知って、この多項式を完全に定義します。 この多項式のすべてのパラメーターがわかっているので、2番目のポイントで1次および2次導関数の値を計算できます。これらは2番目の間隔で多項式の1次および2次導関数の値と一致するため、2次多項式も決定するという事実につながります：



$$$S_2（x_2）= y_2$



$$$S_2（x_3）= y_3$



$$$S_ {2} ^ {'}（x_2）= S_ {1} ^ {'}（x_2）$ -から計算 $$$S_1$



$$$S_ {2} ^ {''}（x_2）= S_ {1} ^ {''}（x_2）$ -から計算 $$$S_1$



同様に、3番目の多項式、4番目、5番目などを、どれだけ多くても考慮します。 つまり、実際には、スプライン全体を再作成します。 しかし、私たちが取ったので $$$S_ {1} ^ {''}（x_1）= 0$ 完全にランダムに、これは導関数につながります $$$k_2$ スプラインの右端でユーザーが設定したものは微分と一致しません $$$S_ {n-1} ^ {'}（x_n）$ 、このような計算の過程で得たものです。 しかし、導関数の意味は $$$S_ {n-1} ^ {'}（x_n）$ スプラインの右端は、2次導関数の値に依存する関数です $$$S_ {1} ^ {''}（x_1）$ 左端に：



$$$S_ {n-1} ^ {'}（x_n）= f（S_ {1} ^ {' '}（x_1））$



そして、与えられた条件を満たすスプラインが存在することが保証され、単一のコピーに存在するため、これは、違いを考慮することができることを意味します。



$$$delta = S_ {n-1} ^ {'}（x_n）-k_2$



そしてその価値を見つけようとする $$$S_ {1} ^ {''}（x_1）$ どこで $$$デルタ$ 0になります-それが正しい値になります $$$S_ {1} ^ {''}（x_1）$ ユーザーが探しているスプラインを構築します：











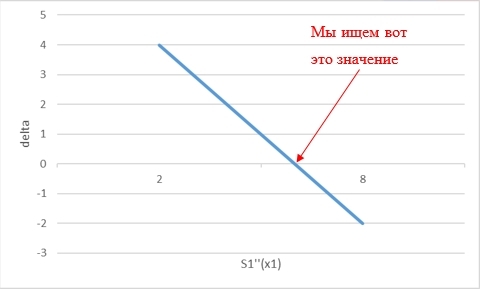
私のアイデアの素晴らしい点は、この依存性が線形になったことです（スプラインを描く点の数に関係なく、この事実は理論計算によって証明されます）。つまり、任意の2つの初期値 $$$S_ {11} ^ {''}（x_1）$ そして $$$S_ {12} ^ {''}（x_1）$ 数える $$$delta_1$ そして $$$delta_2$ 、すぐに目的のスプラインが構築する非常に正しい値を計算します。



$$$S_ {REAL} ^ {''}（x_1）=-delta_2 \ frac {S_ {12} ^ {''}（x_1）-S_ {11} ^ {''}（x_1）} {delta_2-delta_1}$



合計で、このような計算を3回実行するために必要なスプラインを見つけることが保証されています。

プログラムのコードとスクリーンショット

class CPoint { public int X { get; } public int Y { get; } public double Df { get; set; } public double Ddf { get; set; } public CPoint(int x, int y) { X = x; Y = y; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 class CSplineSubinterval { public double A { get; } public double B { get; } public double C { get; } public double D { get; } private readonly CPoint _p1; private readonly CPoint _p2; public CSplineSubinterval(CPoint p1, CPoint p2, double df, double ddf) { _p1 = p1; _p2 = p2; B = ddf; C = df; D = p1.Y; A = (_p2.Y - B * Math.Pow(_p2.X - _p1.X, 2) - C * (_p2.X - _p1.X) - D) / Math.Pow(_p2.X - _p1.X, 3); } public double F(int x) { return A * Math.Pow(x - _p1.X, 3) + B * Math.Pow(x - _p1.X, 2) + C * (x - _p1.X) + D; } public double Df(int x) { return 3 * A * Math.Pow(x - _p1.X, 2) + 2 * B * (x - _p1.X) + C; } public double Ddf(int x) { return 6 * A * (x - _p1.X) + 2 * B; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 class CSpline { private readonly CPoint[] _points; private readonly CSplineSubinterval[] _splines; public double Df1 { get { return _points[0].Df; } set { _points[0].Df = value; } } public double Ddf1 { get { return _points[0].Ddf; } set { _points[0].Ddf = value; } } public double Dfn { get { return _points[_points.Length - 1].Df; } set { _points[_points.Length - 1].Df = value; } } public double Ddfn { get { return _points[_points.Length - 1].Ddf; } set { _points[_points.Length - 1].Ddf = value; } } public CSpline(CPoint[] points) { _points = points; _splines = new CSplineSubinterval[points.Length - 1]; } public void GenerateSplines() { const double x1 = 0; var y1 = BuildSplines(x1); const double x2 = 10; var y2 = BuildSplines(x2); _points[0].Ddf = -y1 * (x2 - x1) / (y2 - y1); BuildSplines(_points[0].Ddf); _points[_points.Length - 1].Ddf = _splines[_splines.Length - 1].Ddf(_points[_points.Length - 1].X); } private double BuildSplines(double ddf1) { double df = _points[0].Df, ddf = ddf1; for (var i = 0; i < _splines.Length; i++) { _splines[i] = new CSplineSubinterval(_points[i], _points[i + 1], df, ddf); df = _splines[i].Df(_points[i + 1].X); ddf = _splines[i].Ddf(_points[i + 1].X); if (i < _splines.Length - 1) { _points[i + 1].Df = df; _points[i + 1].Ddf = ddf; } } return df - Dfn; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

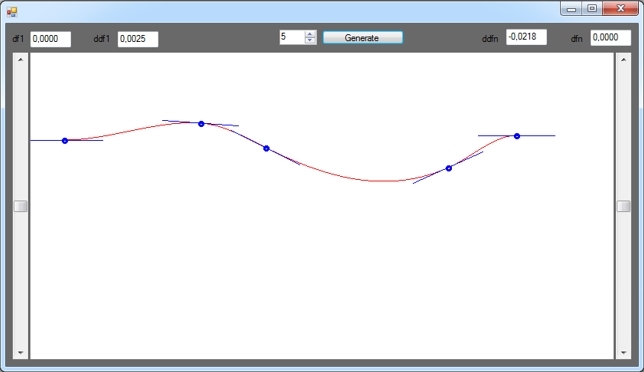
青いセグメントは、対応する点でのスプラインの一次導関数です。 明確にするために、このようなグラフィック要素を追加しました。

アルゴリズムの長所と短所

率直に言って、私は深刻な分析を行っていません。 テストを書いて、さまざまな条件下での動作を確認するといいでしょう（少数/多数の補間ポイント、ポイント間で等しい/任意、線形/正方形/立方/三角関数など）。しかし、私はこれをしませんでしたごめんなさい:)



私が言ったように、ポイントの数に関係なく、2回の計算で区間の左端で2次導関数の正しい値を取得し、もう1つはスプラインを作成するため、アルゴリズムの複雑さはO（N）であると言えます。



ただし、誰かがコードを掘り下げて、このアルゴリズムのより詳細な分析を行いたい場合、私は喜んでいます。 結果について以外は私に書いてください、私は興味があります。

それでは、IQテストは何をしたのでしょうか？

記事の冒頭で、2つの数字シリーズを作成し、続行するように依頼しました。 これは、あらゆる種類のIQテストでよくある質問です。 原則として、質問は質問ですが、少し深く掘り下げると、それはむしろ妄想的であることがわかります。なぜなら、ある欲求では、「正しい」答えがないことを証明できるからです。



一連の「2、4、6、8 、?」から始めましょう。

この数値シリーズを値のペアのセットとして想像してください $$${x_i、y_i}$ ：











どこに $$$y_i$ 番号自体を取得し、 $$$x_i$ -この番号のシリアル番号。 どのような価値があるべきか $$$y_5$ ？



私がスムーズにもたらそうとしている考えは、私たちは絶対にあらゆる価値を代用できるということです。 結局、そのようなタスクを実際にチェックするのは何ですか？ 利用可能なすべての番号を接続する特定のルールを見つけ、このルールに従ってシーケンス内の次の番号を推測する人の能力。 科学用語では、ここでの問題は外挿です（内挿のタスクは特定の間隔内のすべてのポイントを通過する曲線を見つけることであり、外挿のタスクはこの曲線を間隔外で継続することで、将来の曲線の動作を「予測」します）。 したがって、外挿には明確な解決策がありません。 一般的に。 決して。 そうでなければ、人々は人類の全歴史の天気予報を事前に予測し、ルーブル為替レートは決して驚きではなかったでしょう。



もちろん、この問題の正しい答えはまだそこにあり、それは10であり、これらすべての数値をつなぐ「法則」は $$$y = 2x_i$











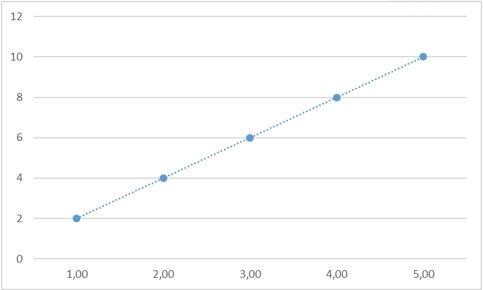
しかし、私たちは他の意味を取ります-それを正当化する法律を見つけることもできます：



$$$y_5 = 12 \ to y = \ frac {x ^ 4} {12}-\ frac {5x ^ 3} {6} + \ frac {35x ^ 2} {12}-\ frac {13x} {6} + 2$









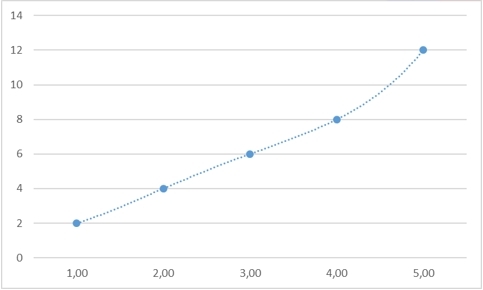
$$$y_5 = 16 \ to y = \ frac {x ^ 4} {4}-\ frac {5x ^ 3} {2} + \ frac {35x ^ 2} {4}-\ frac {21x} {2} + 6$









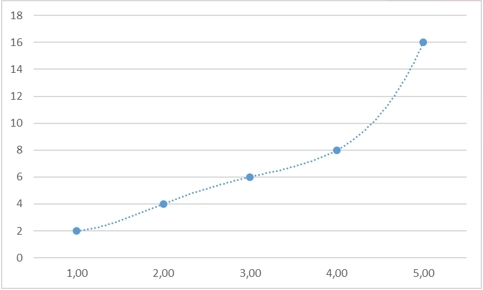
$$$y_5 = -1 \ to y =-\ frac {11x ^ 4} {24} + \ frac {55x ^ 3} {12}-\ frac {385x ^ 2} {24} + \ frac {299x} {12 } -11$









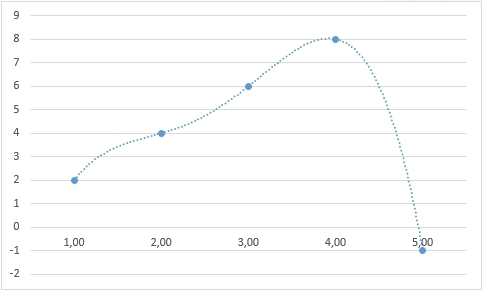
さて、外挿が整理されているため、理論的にも明確な解決策はありません。 しかし、2番目の行で不足している番号を見つけることができますか？











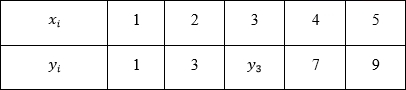
正解だと思う $$$y_3 = 1$ 。 誰が挑戦できますか？ :)



$$$y = -x ^ 4 + 12x ^ 3-49x ^ 2 + 80x-41$

Gitリポジトリ

前回、プロジェクトをリポジトリ内のコードとしてではなく、クラウド内のアーカイブとして投稿したことでscられたため、今回はこのエラーを修正しました： github.com/WieRuindl/Splines