Theano / Lasagne Deep Learning Libraries

こんにちは、Habr！

オープンマシンラーニングコースに関する記事の公開と並行して、ニューラルネットワークとディープラーニングの一般的なフレームワークの使用に関する別のシリーズを開始することにしました。

このシリーズは、機械学習システムの開発に使用されるライブラリであるTheanoの記事で、 Lasagne 、 Keras 、 Blocksなどの高レベルライブラリのコンピューティングバックエンドとして、このシリーズを開きます。

Theanoは2007年以来、主にモントリオール大学のMILAチームによって開発されており、古代ギリシャの女性哲学者で数学者のFeanoにちなんで名付けられました（写真に写っているはずです）。 主な原則は、numpyとの統合、さまざまなコンピューティングデバイス（主にGPU）の透過的な使用、最適化されたCコードの動的生成です。

次の計画を順守します。

• 深層学習ライブラリに関する序文または叙情的な余談
• はじめに
  
  
  • 設置
  • カスタマイズ
• 基本
  
  
  • 最初のステップ
  • 変数と関数
  • 関数についての共有変数など
  • デバッグ
• Theanoでの機械学習
  
  
  • ロジスティック回帰
  • SVM
  • 非線形機能
• ラザニア
  
  
  • 多層パーセプトロン
• おわりに

この投稿のサンプルを含むコードはこちらにあります 。

深層学習ライブラリに関する序文または叙情的な余談

現在、ニューラルネットワークを操作するためのライブラリが多数開発されており、それらはすべて実装が大幅に異なる場合がありますが、命令型とシンボリック型の2つの主なアプローチを特定できます。 ¹

それらがどのように異なるかの例を見てみましょう。 単純な式を計算するとします

$$

$$\ begin {array} {rcl} \ vec a＆：=＆\ left [10、10、\ ldots、10 \ right] ^ T \\ \ vec b＆：=＆2 \ cdot \ vec a \\ \ vec c＆=＆\ vec a \ otimes \ vec b \\ \ vec d＆=＆\ vec c + 1 \ end {array}$$

これは、Pythonの命令型プレゼンテーションでどのように見えるかです：

a = np.ones(10) b = np.ones(10) * 2 c = b * a d = c + 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

インタプリタはコードを1行ずつ実行し、結果を変数a



、 b



、 c



、およびd



に保存します。

シンボリックパラダイムの同じプログラムは、次のようになります。

  A = Variable('A') B = Variable('B') C = B * A D = C + Constant(1) #   f = compile(D) #  d = f(A=np.ones(10), B=np.ones(10)*2)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

大きな違いは、 D



を宣言するときに実行が発生しないことです。計算グラフのみを設定し、それをコンパイルして最終的に実行します。

どちらのアプローチにも長所と短所があります。 まず第一に、命令型プログラムはより柔軟で、視覚的で、デバッグが容易です。 使用するプログラミング言語の豊富な機能をすべて使用できます。たとえば、ループやブランチは、デバッグ目的で中間結果を表示します。 このような柔軟性は、まず、インタープリターに課せられる小さな制限によって実現されます。インタープリターは、その後の変数の使用に備えなければなりません。

一方、シンボリックパラダイムはより多くの制限を課しますが、計算はメモリと実行速度の両方でより効率的です：コンパイル段階では、いくつかの最適化を適用し、未使用の変数を特定し、計算を実行し、メモリを再利用するなどができます。 シンボリックプログラムの特徴は、グラフの宣言、コンパイル、実行の個々の段階です。

命令型パラダイムはほとんどのプログラマーに馴染みがあり、シンボリックなパラダイムは珍しいように見えるかもしれないので、私たちはこれについて詳細に説明します。

この問題をより詳細に理解したい人のために、 MXNetのドキュメントの対応するセクションを読むことをお勧めします（このライブラリについては別の投稿を書きます）。それをコンパイルして実行します。

しかし、十分な理論、例でTheanoに対処しましょう。

設置

インストールには、2.6または3.3より古いpythonバージョン（より良い開発バージョン）、C ++コンパイラー（g ++ for LinuxまたはWindows、clang for MacOS）、 線形代数プリミティブライブラリー （例えばATLAS、OpenBLAS、Intel MKL）、NumPyおよびシピー

GPUで計算を実行するには、CUDAが必要です。また、ニューラルネットワークで見られる多くの操作は、cuDNNを使用して高速化できます。 バージョン0.8.0から、Theano開発者はlibgpuarrayの使用を推奨しています。これにより、複数のGPUを使用することも可能になります。

すべての依存関係がインストールされたら、 pip



Theanoをインストールできます。

 #   pip install Theano #     pip install --upgrade https://github.com/Theano/Theano/archive/master.zip
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

カスタマイズ

Theanoは3つの方法で構成できます。

• theano.config
  
  
  
  オブジェクトtheano.config
  
  
  
  属性を目的の値にtheano.config
  
  
  
  
• 環境変数THEANO_FLAGS
  
  
  
  経由
• $HOME/.theanorc
  
  
  
  構成ファイル（またはWindowsの場合は$HOME/.theanorc.txt
  
  
  
  ）を$HOME/.theanorc.txt
  
  
  
  て

通常、この構成ファイルのようなものを使用します。

 [global] device = gpu #  ,       - GPU  CPU floatX = float32 optimizer_including=cudnn allow_gc = False # ,     #exception_verbosity=high #optimizer = None #    #profile = True #profile_memory = True config.dnn.conv.algo_fwd = time_once #         config.dnn.conv.algo_bwd = time_once [lib] Cnmem = 0.95 #   CNMeM (https://github.com/NVIDIA/cnmem) -  CUDA-
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

構成の詳細については、 ドキュメントを参照してください。

基本

最初のステップ

すべてがインストールされ、構成されたので、たとえば、多項式の値を計算するなど、いくつかのコードを書きましょう。 $$$x ^ 2 + 2x + 1$ ポイント10で：

 import theano import theano.tensor as T #  theano- a = T.lscalar() #   expression = 1 + 2 * a + a ** 2 #  theano- f = theano.function( inputs=[a], #  outputs=expression #  ) #   f(10) >>> array(121)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで4つのことを行いました。long型のスカラー変数



定義し、多項式を含む式を作成し、関数f



定義およびコンパイルし、数値10を入力に渡して実行します。

Theanoの変数には型が付けられており、変数の型にはデータ型とその次元の両方に関する情報が含まれているという事実に注意を払いましょう。 一度に複数のポイントで多項式を計算するに



、aをベクトルとして決定する必要があります。

 a = T.lvector() expression = 1 + 2 * a + a ** 2 f = theano.function( inputs=[a], outputs=expression ) arg = arange(-10, 10) res = f(arg) plot(arg, res, c='m', linewidth=3.)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

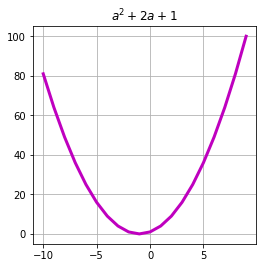
この場合、初期化中に変数の次元数を指定するだけで済みます。各次元のサイズは、関数呼び出しの段階で自動的に計算されます。

UPD：線形代数装置が機械学習で広く使用されていることは秘密ではありません：例は特徴ベクトルによって記述され、モデルパラメーターは行列の形式で記述され、画像は3次元テンソルの形式で表されます。 スカラー量、ベクトル、および行列は、テンソルの特殊なケースと見なすことができます;したがって、これは将来これらの線形代数のオブジェクトと呼ばれるものです。 テンソルとは、数値のN



次元配列を意味します。

theano.tensor



パッケージには、最も一般的に使用されるタイプのテンソルが含まれていますが、 タイプを判別することは難しくありません。

タイプが一致しない場合、Theanoは例外をスローします。 ちなみにこれを修正するには、関数の動作をさらに変更するだけでなく、引数allow_input_downcast=True



コンストラクターに渡すことでできます。

 x = T.dmatrix('x') v = T.fvector('v') z = v + x f = theano.function( inputs=[x, v], outputs=z, allow_input_downcast=True ) f_fail = theano.function( inputs=[x, v], outputs=z ) print(f(ones((3, 4), dtype=float64), ones((4,), dtype=float64)) >>> [[ 2. 2. 2. 2.] >>> [ 2. 2. 2. 2.] >>> [ 2. 2. 2. 2.]] print(f_fail(ones((3, 4), dtype=float64), ones((4,), dtype=float64)) >>> --------------------------------------------------------------------------- >>> TypeError Traceback (most recent call last)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

一度に複数の式を計算することもできます。この場合のオプティマイザーは、交差する部分、この場合は合計を再利用できます $$$x + y$ ：

 x = T.lscalar('x') y = T.lscalar('y') square = T.square(x + y) sqrt = T.sqrt(x + y) f = theano.function( inputs=[x, y], outputs=[square, sqrt] ) print(f(5, 4)) >>> [array(81), array(3.0)] print(f(2, 2)) >>> [array(16), array(2.0)]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

関数間で状態を交換するには、特別な共有変数が使用されます。

 state = theano.shared(0) i = T.iscalar('i') inc = theano.function([i], state, #    updates=[(state, state+i)]) dec = theano.function([i], state, updates=[(state, state-i)]) #         print(state.get_value()) inc(1) inc(1) inc(1) print(state.get_value()) dec(2) print(state.get_value()) >>> 0 >>> 3 >>> 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そのような変数の値は、テンソル変数とは異なり、通常のpythonコードからTheano関数の外部で取得および変更できます。

 state.set_value(-15) print(state.get_value()) >>> -15
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

共有変数の値は、テンソル変数で「置換」できます。

 x = T.lscalar('x') y = T.lscalar('y') i = T.lscalar('i') expression = (x - y) ** 2 state = theano.shared(0) f = theano.function( inputs=[x, i], outputs=expression, updates=[(state, state+i)], #    state    y givens={ y : state } ) print(f(5, 1)) >>> 25 print(f(2, 1)) >>> 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

デバッグ

Theanoは、グラフの計算とデバッグを表示するための多くのツールを提供します。 ただし、シンボリック式のデバッグはまだ簡単な作業ではありません。 ここでは、最もよく使用されるアプローチを簡単にリストします。デバッグの詳細については、ドキュメントを参照してください： http : //deeplearning.net/software/theano/tutorial/printing_drawing.html

各関数の計算グラフを印刷できます。

 x = T.lscalar('x') y = T.lscalar('y') square = T.square(x + y) sqrt = T.sqrt(x + y) f = theano.function( inputs=[x, y], outputs=[square, sqrt] ) #       theano.printing.debugprint(f)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

合計は一度だけ計算されることに注意してください。

 Elemwise{Sqr}[(0, 0)] [id A] '' 2 |Elemwise{add,no_inplace} [id B] '' 0 |x [id C] |y [id D] Elemwise{sqrt,no_inplace} [id E] '' 1 |Elemwise{add,no_inplace} [id B] '' 0
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

式は、より簡潔な形式で表示できます。

 #   W = T.fmatrix('W') b = T.fvector('b') X = T.fmatrix('X') expr = T.dot(X, W) + b prob = 1 / (1 + T.exp(-expr)) pred = prob > 0.5 #    theano.pprint(pred) >>> 'gt((TensorConstant{1} / (TensorConstant{1} + exp((-((X \\dot W) + b))))), TensorConstant{0.5})'
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

または、グラフの形式で：

 theano.printing.pydotprint(pred, outfile='pics/pred_graph.png', var_with_name_simple=True)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

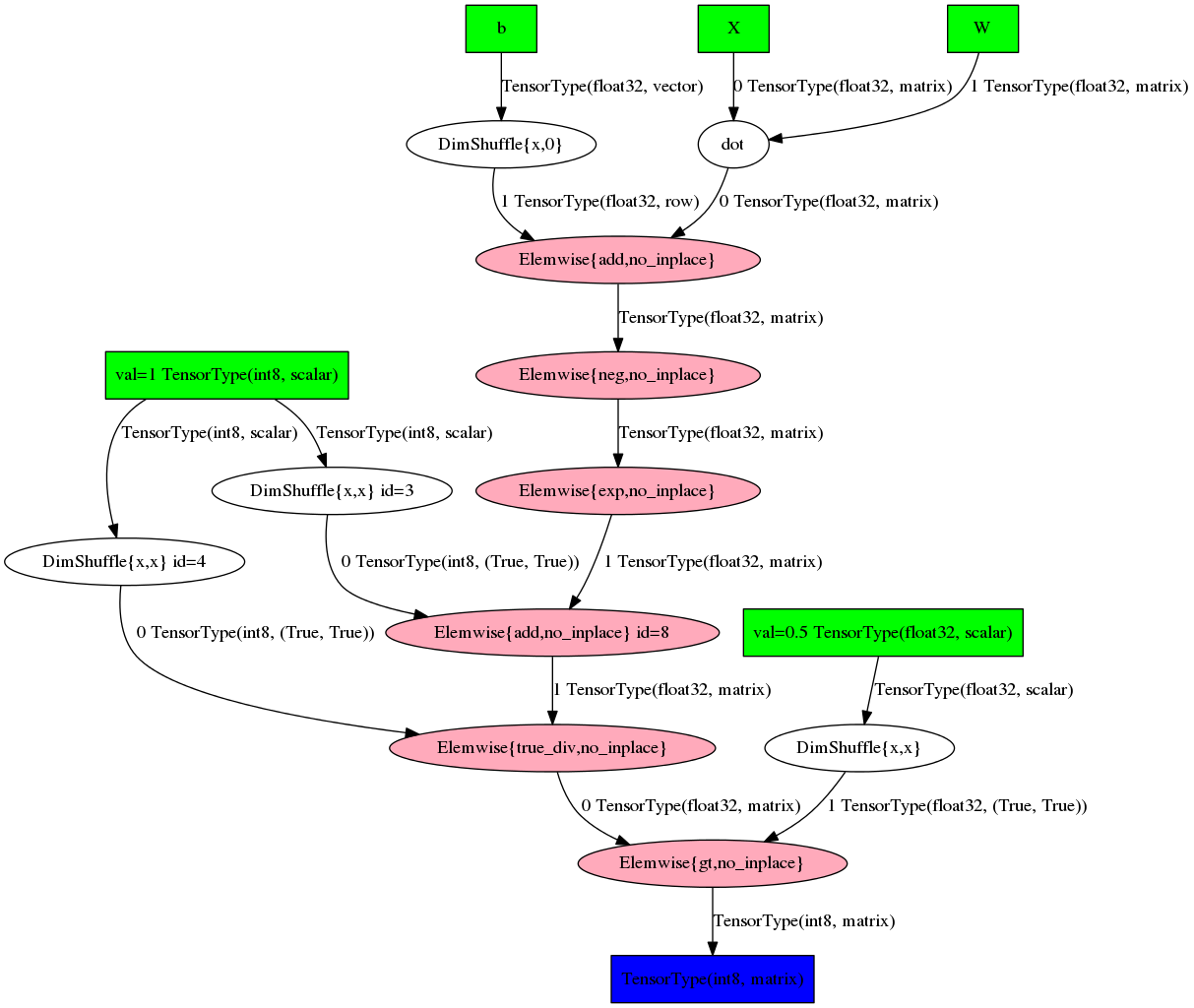
残念ながら、このようなグラフの可読性は、式の複雑さが増すにつれて急激に低下します。 実際、何かはおもちゃの例でしか理解できません。

Theanoでの機械学習

ロジスティック回帰

ロジスティック回帰の例、Theanoを使用して機械学習アルゴリズムを開発する方法を見てみましょう。 このモデルがどのように構成されているかの詳細には意図的に入りません（これを対応する公開コースの記事に任せましょう）が、クラスの事後確率は思い出してください $$$C_1$ 形をしています $$$p（C_1 | X）= \ hat {y} = \ sigma（w ^ TX + b）$

モデルのパラメーターを定義してみましょう。便宜上、オフセットに別のパラメーターを導入します。

 W = theano.shared( value=numpy.zeros((2, 1),dtype=theano.config.floatX), name='W') b = theano.shared( value=numpy.zeros((1,), dtype=theano.config.floatX), name='b')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、記号とクラスラベルのシンボリック変数を取得します。

 X = T.matrix('X') Y = T.imatrix('Y')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

事後確率とモデル予測の式を定義しましょう：

 linear = T.dot(X, W) + b p_y_given_x = T.nnet.sigmoid(linear) y_pred = p_y_given_x > 0.5
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、次の形式の損失関数を定義します。 $$$L =-\ frac {1} {N} \ sum_ {n = 1} ^ {N} [y \ log {\ hat {y}} +（1-y）\ log {（1-\ hat {y }）}]$

 loss = T.nnet.binary_crossentropy(p_y_given_x, Y).mean()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

シグモイドとクロスエントロピーの式を明示的に記述したのではなく、 theano.tensor.nnet



パッケージの関数を使用しました。これは、機械学習で一般的な多くの関数の最適化された実装を提供します。 さらに、このパッケージの機能には通常、数値安定性のための追加のトリックが含まれています。

損失関数を最適化するには、勾配降下法を使用します。その方法の各ステップは次の式で与えられます。

$$

$$\大きいw_ {n + 1} = w_n-\ eta \ frac {1} {n} \ nabla E（w_n）$$

コードに変換しましょう：

 g_W = T.grad(loss, W) g_b = T.grad(loss, b) updates = [(W, W - 0.04 * g_W), (b, b - 0.08 * g_b)]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでは、Theanoの素晴らしい機会を活用しました-自動² 差別化。 T.grad



の呼び出しは、最初の引数の2番目の引数に対する勾配を含む式を返しました。 このような単純なケースではこれは不要に思えるかもしれませんが、大規模なマルチレイヤーモデルを構築する場合に役立ちます。

勾配が取得されると、Theano関数のみをコンパイルできます。

 train = theano.function( inputs=[X, Y], outputs=loss, updates=updates, allow_input_downcast=True ) predict_proba = theano.function( [X], p_y_given_x, allow_input_downcast=True )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、反復プロセスを開始します。

 sgd_weights = [W.get_value().flatten()] for iter_ in range(4001): loss = train(x, y[:, np.newaxis]) sgd_weights.append(W.get_value().flatten()) if iter_ % 100 == 0: print("[Iteration {:04d}] Train loss: {:.4f}".format(iter_, float(loss)))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

生成したデータの場合、プロセスは次のような境界線に収束します。

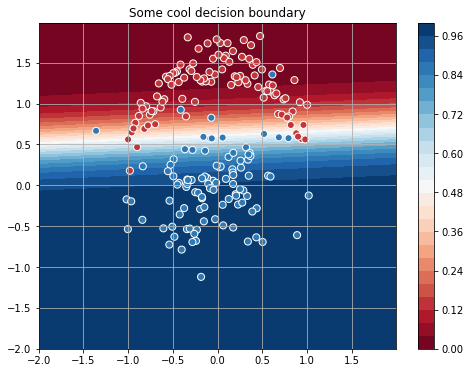
よさそうに見えますが、このような単純なタスクの4000回の反復は少し多いようです...最適化を高速化し、Newtonメソッドを使用してみましょう。 この方法は、損失関数の2次導関数を使用し、次のような一連のステップです。

$$

$$\大w_ {n + 1} = w_n-H ^ {-1} \ nabla E（w_n）$$

どこで $$$H$ - ヘッセ行列。

ヘッセ行列を計算するには、モデルのパラメーターの1次元バージョンを作成します。

 W_init = numpy.zeros((2,),dtype=theano.config.floatX) W_flat = theano.shared(W_init, name='W') W = W_flat.reshape((2, 1)) b_init = numpy.zeros((1,), dtype=theano.config.floatX) b_flat = theano.shared(b_init, name='b') b = b_flat.reshape((1,))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、オプティマイザーのステップを定義します。

 h_W = T.nlinalg.matrix_inverse(theano.gradient.hessian(loss, wrt=W_flat)) h_b = T.nlinalg.matrix_inverse(theano.gradient.hessian(loss, wrt=b_flat)) updates_newton = [(W_flat, W_flat - T.dot(h_W , g_W)), (b_flat, b_flat - T.dot(h_b, g_b))]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

同じ結果に達しましたが、

、

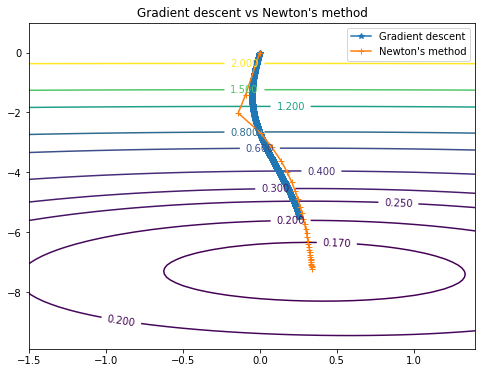
Newtonの方法では、必要なステップは30（勾配降下の場合は4000）だけでした。

両方の方法のパスはこのグラフで見ることができます：

Svc

サポートベクターメソッドを簡単に実装することもできます。このため、損失関数を次の形式で表すだけで十分です。

$$

$$\ large C \ sum_ {n = 1} ^ {N} [1-w ^ T \ phi（x）+ b] _ + + || w || ^ 2$$

Theanoに関しては、これは前の例のいくつかの行を置き換えることで書くことができます：

 C = 10. loss = C * T.maximum(0, 1 - linear * (Y * 2 - 1)).mean() + T.square(W).sum() predict = theano.function( [X], linear > 0, allow_input_downcast=True )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

$$$C$ これは、モデルを正規化するハイパーパラメーターであり、式 $$$（Y * 2-1）$ ラベルを範囲に入れるだけです $$$\ {-1、1 \}$

選択されたCの場合、分類器は次のようにスペースを分割します。

非線形機能

ループは、プログラミングで最もよく使用される構造の1つです。 Theanoループのサポートは、 スキャン機能で表されます。 それがどのように機能するかを知りましょう。 読者には、特徴の線形関数が生成されたデータを分割するための最良の候補ではないことはすでに明らかだと思います。 この欠点は、元のものに多項式の特徴を追加することで修正できます（この手法については 、ブログの別の記事で詳しく説明しています）。 だから、私はフォームの変換を取得したい $$$\ {x_1、x_2 \} \ rightarrow \ bigcup \ limits_ {i = 0} ^ {i = K} \ {x_1 ^ i、x_2 ^ i \}$ 。 Pythonでは、たとえば次のように実装できます。

 poly = [] for i in range(K): poly.extend([x**i for x in features])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Theanoでは、次のようになります。

 def poly(x, degree=2): result, updates = theano.scan( #  ,      fn=lambda prior_result, x: prior_result * x, #    outputs_info=T.ones_like(x), # ,  x       fn non_sequences=x, #   n_steps=degree) #      N x M*degree return result.dimshuffle(1, 0, 2).reshape((result.shape[1], result.shape[0] * result.shape[2]))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

scan



の最初の関数が渡され、各反復で呼び出されます。その最初の引数は前の反復の結果であり、後続のnon_sequences



はすべてnon_sequences



です。 outputs_info



は、 x



と同じ次元とタイプの出力テンソルを初期化し、単位で埋めます。 n_steps



は、必要な反復回数を示します。

scan



は、サイズ(n_steps, ) + outputs_info.shape



テンソルの形式で結果を返すため、必要な符号を取得するためにマトリックスに変換します。

結果の式の操作を簡単な例で説明します。

 [[1, 2], -> [[ 1, 2, 1, 4], [3, 4], -> [ 3, 4, 9, 16], [5, 6]] -> [ 5, 6, 25, 36]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

努力を活用するには、モデルの定義を変更し、パラメーターを追加するだけです（より多くの兆候があるため）。

 W = theano.shared( value=numpy.zeros((8, 1),dtype=theano.config.floatX), name='W') linear = T.dot(poly(X, degree=4), W) + b
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

新機能により、クラスを大幅に分離することができます。

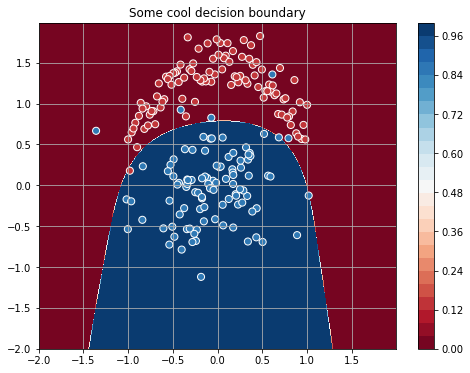
ニューラルネットワークとラザニア³

この時点で、Theanoで機械学習システムを作成する主な段階、つまり入力変数の初期化、モデルの定義、Theano関数のコンパイル、オプティマイザーのステップを含むサイクルについては既に説明しました。 これで終わりかもしれませんが、Theanoの上で動作するニューラルネットワーク用の素晴らしいライブラリであるLasagneを読者に紹介したいと思います。 Lasagneは、レイヤー、最適化アルゴリズム、損失関数、パラメーターの初期化など、既製のコンポーネントのセットを提供しますが、Theanoは抽象化の多数のレイヤーの後ろに隠れません。

MNIST分類の例を使用して、典型的なTheano / Lasagneコードがどのように見えるかを見てみましょう。

それぞれ800ニューロンの2つの隠れ層を持つ多層パーセプトロンを構築します。正規化のためにドロップアウトを使用し、このコードを別の関数に配置します。

 def build_mlp(input_var=None): #  ,    # (  minibatch'a, 1 , 28   28 ) #        , #        network = lasagne.layers.InputLayer( shape=(None, 1, 28, 28), input_var=input_var) # dropout  20%    network = lasagne.layers.DropoutLayer(network, p=0.2) #    800   ReLU    #    ,  Xavier Glorot  Yoshua Bengio network = lasagne.layers.DenseLayer( network, num_units=800, nonlinearity=lasagne.nonlinearities.rectify, W=lasagne.init.GlorotUniform()) #  dropout   50%: network = lasagne.layers.DropoutLayer(network, p=0.5) #      network = lasagne.layers.DenseLayer( network, num_units=800, nonlinearity=lasagne.nonlinearities.rectify) network = lasagne.layers.DropoutLayer(network, p=0.5) # ,    10 : network = lasagne.layers.DenseLayer( network, num_units=10, nonlinearity=lasagne.nonlinearities.softmax) return network
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このようなシンプルで完全に接続されたネットワークを取得します。

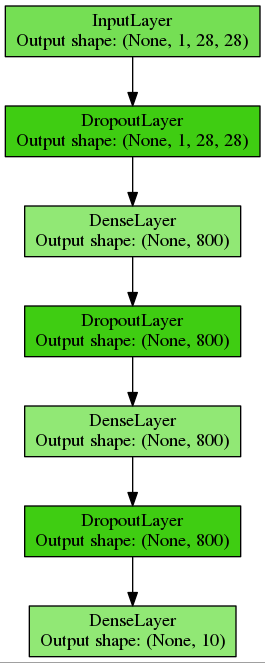
テンソル変数を初期化し、トレーニングと検証のためにTheano関数をコンパイルします。

 input_var = T.tensor4('inputs') target_var = T.ivector('targets') #      network = build_mlp(input_var) #      ,   prediction = lasagne.layers.get_output(network) #    loss = lasagne.objectives.categorical_crossentropy(prediction, target_var).mean() #     L1  L2 , . lasagne.regularization. #        #    keyword ,      #     trainable  regularizable params = lasagne.layers.get_all_params(network, trainable=True) #         updates = lasagne.updates.nesterov_momentum( loss, params, learning_rate=0.01, momentum=0.9) #        . #       deterministic=True, #   dropout test_prediction = lasagne.layers.get_output(network, deterministic=True) test_loss = T.nnet.categorical_crossentropy(test_prediction, target_var).mean() #     test_acc = T.mean( T.eq(T.argmax(test_prediction, axis=1), target_var), dtype=theano.config.floatX) #     train = theano.function( inputs=[input_var, target_var], outputs=loss, updates=updates) #   —   #  Theano  ,        #      validate = theano.function( inputs=[input_var, target_var], outputs=[test_loss, test_acc])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、トレーニングサイクルを作成します。

 print("| Epoch | Train err | Validation err | Accuracy | Time |") print("|------------------------------------------------------------------------|") try: for epoch in range(100): #         train_err = 0 train_batches = 0 start_time = time.time() for batch in iterate_minibatches(X_train, y_train, 500, shuffle=True): inputs, targets = batch train_err += train(inputs, targets) train_batches += 1 #     val_err = 0 val_acc = 0 val_batches = 0 for batch in iterate_minibatches(X_val, y_val, 500, shuffle=False): inputs, targets = batch err, acc = validate(inputs, targets) val_err += err val_acc += acc val_batches += 1 print("|{:05d} | {:4.5f} | {:16.5f} | {:10.2f} | {:7.2f} |".format (epoch, train_err / train_batches, val_err / val_batches, val_acc / val_batches * 100, time.time() - start_time)) except KeyboardInterrupt: print("The training was interrupted on epoch: {}".format(epoch))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果の学習曲線：

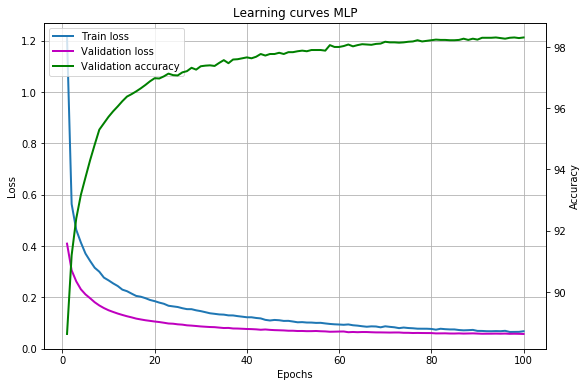
私たちのモデルは98％以上の精度を達成しています。これは、例えば畳み込みニューラルネットワークを使用して間違いなく改善できますが、このトピックはすでにこの記事の範囲外です。

ヘルパーを使用してウェイトを保存およびロードすると便利です。

 #   savez('model.npz', *lasagne.layers.get_all_param_values(network)) network = build_mlp() #  ,  : with np.load('model.npz') as f: param_values = [f['arr_%d' % i] for i in range(len(f.files))] lasagne.layers.set_all_param_values(network, param_values)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Lasagneのドキュメントはこちらから入手できます 。多くの例と事前トレーニングされたモデルは別のリポジトリにあります 。

おわりに

この投稿では、表面的にTheanoの可能性に精通しました。詳細については以下をご覧ください。

• ドキュメントに目を向ける： 1、2
• コード例を見る
• コミュニティとのチャット
• ソースコードを調べる。

投稿の準備を手伝ってくれたbauchgefuehlに感謝します。

---

1. 2つのアプローチの境界はかなり曖昧であり、以下に述べるすべてが厳密に当てはまるわけではなく、例外と境界線のケースが常に存在します。 ここでのタスクは、主なアイデアを伝えることです。

2.テクニカルレポートとドキュメントのTheano開発者は、差別化を象徴的に呼んでいます。 ただし、Habrに関する以前の記事の1つでこの用語を使用すると、 議論が生じました。Theanoのソースコードとウィキペディアの定義に基づいて、著者は正しい用語は依然として「自動差別化」であると考えています。

3.このセクションの資料の大部分は、Lasagneの資料に基づいています。