エスケープ分析とスカラー化：GCを休ませる

今回は、昨年4月にJPoint 2016で行ったEscape AnalysisとScalar Replacementのペアの作業の分析に関するRuslan cheremin Cheremin（ドイツ銀行）のレポートに基づいて、本物のハードコアと準備された資料との技術面接の流れを多様化することにしました。



目の前のビデオレポート：







そして、カットの下に、個々のスライドを含む全文転写を投稿しました。



用語に関する少し叙情的な余談から始めましょう。

エスケープ分析と最適化におけるその場所

エスケープ分析は、オブジェクトのリンクの到達可能領域を静的に（コンパイル時に）決定できるコード分析手法です。 大まかに言って、オブジェクトを割り当てる命令があり、分析中に、別の命令が作成されたオブジェクトへのリンクを何らかの方法で取得できるかどうかを理解しようとします。



エスケープ分析はそれ自体が最適化ではなく、単なる分析ですが、その結果は後続の最適化に使用できます。 通常、通常、命令に対して正確ではない到達可能性に関心がありますが、「何らかのメソッドで作成されたオブジェクトがこのメソッドの外部に到達可能かどうか」のようなものです。 そして、最適化タスクの一部として、答えが「いいえ、オブジェクトはメソッドの外部に到達できない」という状況に最も興味があります。



スカラー置換 スカラ化とは、メソッド内にのみ存在するオブジェクトをローカル変数に置き換えることです。 オブジェクトを取得し（実際にはまだ存在しません-プログラムの実行時に作成されます）、作成する必要はありません：すべてのフィールドをローカル変数に入れ、これらのフィールドを参照するようにコードを変換し、割り当てますコードから消去します。



私は、EA / SRがそのような静的なガベージコレクタであるという比metaが好きです。 通常の（動的な）GCはランタイムで実行され、オブジェクトのグラフをスキャンして到達可能性分析を実行します。到達不能になったオブジェクトを見つけ、使用しているメモリを解放します。 エスケープとスカラー化のペアは、JITコンパイル時に同じことを行います。 エスケープ分析もコードを見て、「この命令の後にここで作成されたオブジェクトはどこにも到達できないため、特定の条件下ではまったく作成できません。」と言います。



いくつかのエスケープ分析とスカラー置換がJavaで長い間登場しました。2009年に最初に実験的なオプションとして登場し、2010年からデフォルトで有効になっています。

結果はありますか？ 狭い円では、2010年に作成されたガベージコレクターの読み込みスケジュールの実際の断片は、ドイツ銀行に送られます。 この図は、最適化のためにまったく何もできないが、次のJavaの更新を待つこともあることを示しています。





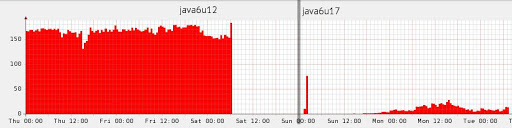
ソース： dolzhenko.blogspot.ru



もちろん、これはめったに起こりません。これは例外的なケースです。 より現実的な例では、平均的なアプリケーションのさまざまなソースによると、エスケープ分析は割り当ての約15％を排除でき、幸運な場合は最大70％を排除できます。



2010年にこのツールが登場したとき、私は正直、非常に刺激を受けました。 私はプロジェクトを終えたばかりで、科学的な計算がたくさんありました。特に、あらゆる種類のベクトルを積極的に使いました。 そして、前の命令から次の命令まで生き続ける多くのオブジェクトがありました。 これを見たとき、私はここでCが良いだろうと冷静な考えを持っていました。 そして、この最適化について読んだ後、そのような問題を解決できることに気付きました。 ただし、このリリースでのSunの動作の控えめな例があったため、より詳細な説明（動作する状況、動作しない状況、動作に必要なもの）を待っていました。 そして、私は長い間待ちました。



残念なことに、7年以上にわたり、使用例が3つしかありませんでしたが、そのうちの1つはSunの例です。 すべての例の問題は、記事がコメント付きのコードを引用していることでした：「これがどのように機能するか」。 そして、命令を再配置すると、スカラー化はこれから壊れますか？ そして、ArrayListの代わりにLinkedListを使用すると、機能しますか？ はっきりしませんでした。 その結果、私は他の誰かの研究、つまり この作業を自分で行う必要があります。

実験経路

何を手に入れたいですか？ まず、直感的な理解を求めていました。 明らかに、JITコンパイルは一般的に非常に複雑なものであり、多くのことに依存しています。 詳細を理解するには、Oracleで作業する必要があります。 そのような仕事はありませんでした。 コードを見て、それを評価できるように、直感的に理解する必要があります-ほぼ間違いなくはい） そして、このためには、動作するときと動作しないときを見ることができるいくつかの例が必要です。 そして、これらの例を簡単に記述できるようにするフレームワーク。

私の仕事は実験的なものでした。たとえば、コンピューターにJDKがあります。当局に尋ねることなく、エスケープ分析の原則についてどのような情報を入手できますか。 つまり、これは非常に自然科学的なアプローチです。私たちには、「突っ込んで」、どのように機能するかを見るブラックボックスがほとんどあります。

実験そのものに取りかかる前に、もう少し理論的な余談。 エスケープ分析とスカラー化は、サーバーコンパイラが持つ大規模な最適化の一部にすぎないことを理解することが重要です。 非常に一般的な用語では、C2最適化プロセスが図に示されています。







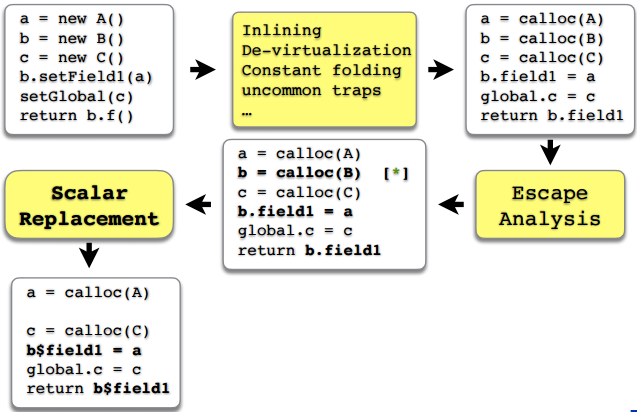
ここで重要なことは、エスケープ分析の前であっても、他の最適化ツールが問題を処理することです。 たとえば、インライン化、仮想化、定数の折り畳み、および頻繁またはまれなルートの強調表示（実際、さらに多くのルートがありますが、ここではエスケープ分析に最も頻繁に影響するルートを示しました）。 そのため、エスケープ分析の結果に従って、一部のオブジェクトがスカラー化されるため、チェーンの以前のすべてのリンク、以前の最適化は、エスケープ分析とスカラー化の前にうまく機能する必要があります。 そして、何かが壊れる可能性があり、それはどの段階でも起こりえませんが、後で見るように、ほとんどの場合、エスケープ分析の直前に何かが壊れます。 そして、場合によってのみ、タスクに対処しないのはエスケープ分析そのものです。

ツールキット

数年前、スカラー化の実験を試みて、主にGarbageCollectorMXBean.getCollectionCount()



依存していました。 これはかなり粗雑なメトリックです。 しかし、より明確な測定値ThreadMBean.getThreadAllocatedBytes(threadId)



があります。これは、スレッドIDによって直接、この特定のスレッドによって割り当てられたバイト数を示します。 実験には他に何も必要ありませんが、最初に使用した最初の古いメトリックを使用して結果を比較しました。 別の制御方法は、適切なキー（ -XX:-EliminateAllocations



）で-XX:-EliminateAllocations



化を無効にし、観察された効果がエスケープ分析によって実際に決定されるかどうかを確認することです。



テスト結果に驚く場合、PrintCompilationキーとPrintInliningキーを使用して、詳細情報を取得できます。 3番目のキーLogCompilationがあります。これは、同じものをより多く、さらにxml形式で生成します。これをJITWatchユーティリティにフィードすると、すべてが美しいUIで表示されます。



論理的な質問は、なぜJMHを使用しないのかということです。 JMHは本当にそれを行うことができます。 プロファイラーである-prof gc



を使用すると、同じ割り当てが出力され、1回の繰り返しに正規化されます。







そして、最初はこちらから入ろうとしました。 しかし、実際のところ、JMHは主にパフォーマンスに重点を置いているため、あまり興味がありません。 繰り返しにどれだけ時間がかかったかについては興味がありません。 特定の最適化がそこで機能したかどうか、言い換えれば、トリガー応答が必要かどうか疑問に思っています。 そして、ここに私がすぐに削除する方法を見つけられなかった多くの情報があります。 最終的に、私は今日、30分以内に結果を取得したい場合、自分でそれを書く方が簡単だと決めました。 したがって、私は自分の「自転車」を持っています。 しかし、誰かがこれらの実験を続けたい、または自分で実験をしたい場合は、標準が通常より良いので、標準ツールを使用することを強くお勧めします。

パート1.基本

例1.1。 ベーシック

簡単なテストから始めましょう：Sunリリースの例に似ています。

単純なVector2Dクラスがあります。 ランダム性の助けを借りて3つのランダムなベクトルを作成し、それらを使用して特定の演算を実行します（スカラー積を追加および計算します）。 最新のJVMでこれを実行すると、ここでいくつのオブジェクトが作成されますか？







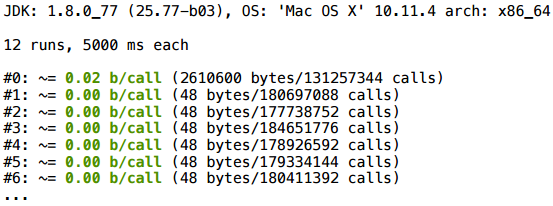
その結果、最初に何かが割り当てられます（コンパイルはまだ渡されていません）。それから、すべてが非常にきれいです-呼び出しごとに0バイト。

これは標準的な例であるため、機能することは驚くことではありません。

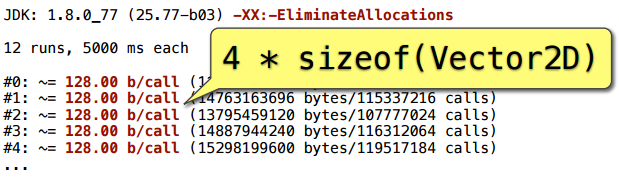
制御のために、割り当ての消去を無効にするキーを追加し、呼び出しごとに128バイトを取得します。 これらはただ4つのVector2Dオブジェクトです。3つは明確に作成され、もう1つは追加中に表示されました。

例1.2 ループ累積

前の例にループを追加します。

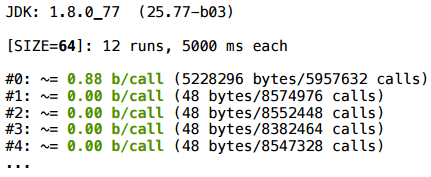
ループ内でベクトルを追加するバッテリーベクトルを開始します。







このシナリオでもすべて順調です（私が調べたSIZE



値について）。

例1.3 ループ内で置換

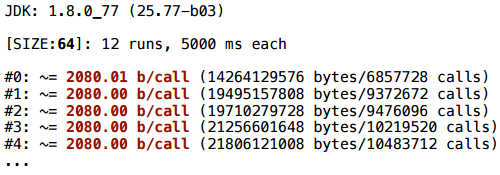
今回は、定数-doubleを乗算し、結果を同じ変数に書き込みます。 これは実際には同じバッテリーです。ここでは、ベクトルにある数を掛けます。





予想外ですが、ここではスカラー化は機能しませんでした（2080バイト= 32 *（SIZE + 1））。







理由を理解する前に、いくつかの例を検討してください。

例1.4 制御フロー

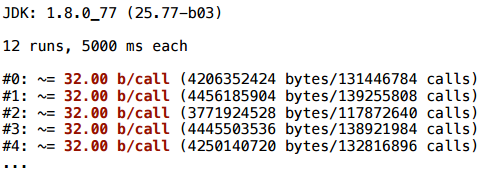
簡単な例：サイクルはありません。条件付き遷移があります。 ランダムに座標を選択し、Vector2Dを作成します。







そして、ここでスカラー化は役に立たない：1つのベクトルが作成されるたびに-それらの同じ32バイト。

例1.5 制御フロー

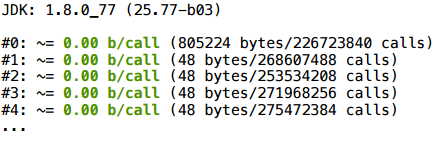
この例を少し変更してみましょう。 ベクトルの作成を両方のブランチ内に追加するだけです。







そして、ここではすべてが完全にスカラー化されています。







絵が現れ始めます-ここで何が起こっていますか？

「ポイントをマージ」

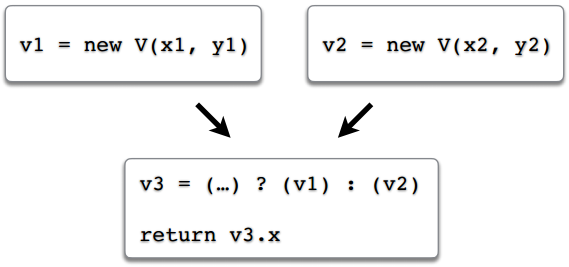
プログラムに実行スレッドがあると想像してください。 v1オブジェクトを作成した1つのブランチと、v2オブジェクトを作成した2番目のブランチがあります。 3番目の変数v3には、実行にかかったルートに応じて、最初のオブジェクトまたは2番目のオブジェクトへのリンクを記述します。 最後に、v3リンクを介してフィールドを返します。 スカラー化が発生し、フィールドv1.x、v1.y、v2.x、v2.yがローカル変数、たとえばv1 $ x、v1 $ y、v2 $ x、v2 $ yになったとします。 そして、v3リンクをどうしますか？ というか、フィールドv3.xへのアピールはどうなるのでしょうか？



これは質問です。 ここや例1.4のようないくつかの簡単な例では、ソリューションは直感的です。このコードがすべてである場合、条件内でステートメントを返すだけで、各ブランチに1つずつ、2つの戻り値があります。 、そしてそれぞれがその値を返します。 しかし、ケースはより複雑であるため、JVM開発者はこのシナリオを単純に最適化しないと判断しました。 一般的な場合、これを行うには-使用するオブジェクトのフィールドを把握します-難しすぎることが判明しました（たとえば、JDK-6853701バグ、またはJVMソースコードの対応するコメントを参照）。



この例をまとめると、次の場合にはスカラー化はありません。

• 参照変数は複数のオブジェクトを指すことができます。
  
  
• これが異なる実行シナリオで発生する場合でも。
  
  

スカラー化の可能性を高めたい場合は、1つのリンクが1つのオブジェクトを指している必要があります。 常に1つのオブジェクトを指しますが、異なる実行シナリオでは異なるオブジェクトになる可能性があります -これでさえ、エスケープ分析を混乱させます。

パート2. EqualsBuilder

これはcommons.langのクラスであり、クラスのフィールドをBuilderに追加することにより、この方法で同等のものを生成できるという考え方です。 正直に言って、私はそれを自分では使用せず、ビルダーの例を必要としていました。 実際の例は通常、合成の例よりも優れています。







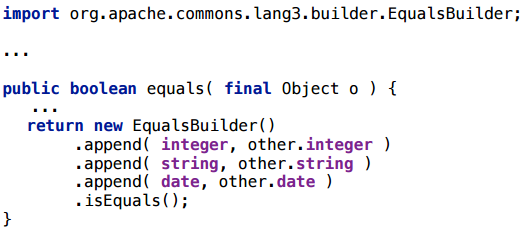
もちろん、すべてのequals呼び出しに対してオブジェクトを作成することはお勧めできませんので、このことをスカラー化するといいでしょう。

例2.1 EqualsBuilder

簡単なコードを書きました-明示的に書かれた2つのintだけです（ただし、フィールドがそこに指定されていても、本質は変わりません）。







この状況はスカラー化されることが予想されます。

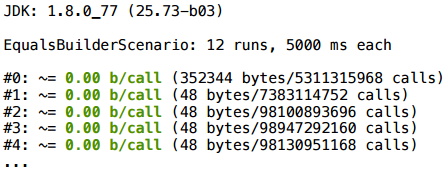
例2.2 EqualsBuilder

例を少し変更してみましょう。2つのintの代わりに、2行を追加します。







その結果、スカラー化は機能しません。







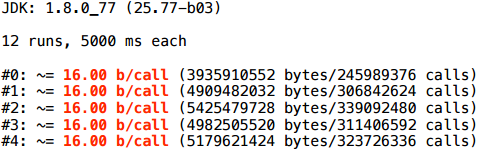
.append（...）メソッドにはまだ入りません。 まず、コンパイラで何が起こるかを少なくとも簡単に伝えるキーがあります。







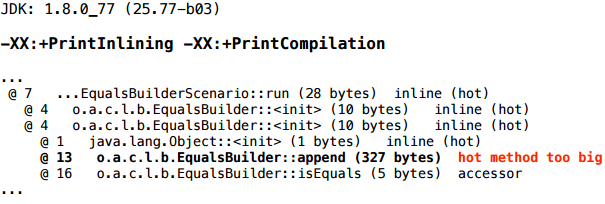
appendメソッドが失敗しなかったため、エスケープ分析が理解できないことがわかりました。ここに、このように.append（）メソッドの内部に入ったビルダーへのリンクがあります。 これは不明です（コンパイラーは.appendメソッドの内部を調べないため、JITはプロシージャー間の最適化を行いません）。 多分彼女はそこでグローバル変数に割り当てられたのでしょう。 そして、そのような状況では、脱出分析は降伏します。



「ホットメソッドが大きすぎる」という診断はどういう意味ですか？ メソッドがホットであること、つまり これは何度も呼び出され、そのバイトコードのサイズは特定の制限であるインライン化しきい値（制限は頻繁なメソッドの制限）よりも大きくなっています。 この制限-FreqInlineSizeキーによって設定され、デフォルトでは325です。診断では327が表示されます-つまり、2バイトだけが欠落しています。

メソッドの内容は次のとおりです-327バイトがあると簡単に信じられます。







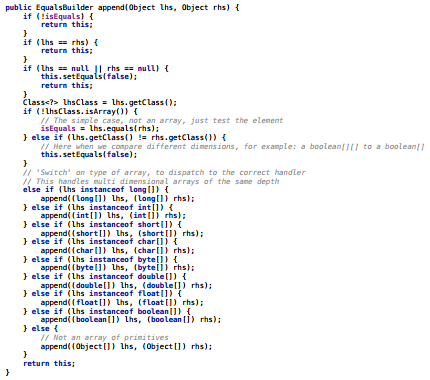
仮説をどのようにテストできますか？ FreqInlineSizeキーを追加し、インライン化のしきい値をたとえば328に増やすことができます。







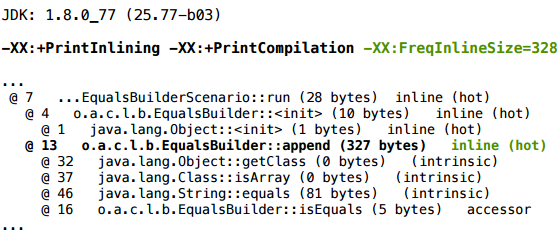
コンパイルプロファイルでは、.append（）がインライン化され、すべてが完全にスケーラブルであることがわかります。







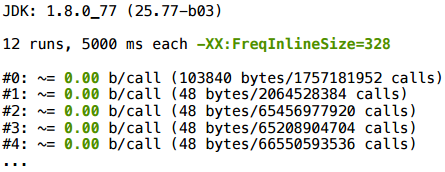
明確にしましょう。JVMフラグ、JITコンパイルオプションを（以下で）変更するとき、状況を修正するのではなく、仮説をテストするためにこれを行います。 JITコンパイルオプションは、特別に訓練された人々によって選択されるため、これらのオプションを使用することはお勧めしません。 もちろん、試してみることはできますが、効果を予測することは困難です。そのようなパラメーターは、何かをスカラー化する特定のメソッドではなく、プログラム全体に影響します。

結論2。

• インライン化はアダプティブランタイムの親友です
  
  
• そして簡潔さは彼を大いに助けます。
  
  

より短いメソッドを記述します。 特に、.append（）の例では、配列で動作する大きなシートがあります-配列の比較を試みます。 別のメソッドに入れるだけで、すべてが完全にインライン化され、スカラー化されます（試しました）。 このインラインヒューリスティックでは、これは非常に黒い動きです（白い場合もあります）：328バイトのメソッドはインラインではありませんが、200バイトの2つのメソッドに完全にインラインで分割されています。

パート3.複数値の戻り値

tupleメソッドから戻ることを検討してください-一度にいくつかの値。

Pairなどの簡単なオブジェクトと、完全に単純な例を見てみましょう。事前に設定されたプールからランダムに選択された2、3の行を返します。 コンパイラがこのコードをまったくスローしないように、副作用を導入します。これらのタイプ文字列で何かをカウントし、結果を返します。







このシナリオはスカラー化されています。 これは非常に実用的な例であり、使用することができます。メソッドがホットでインラインの場合、このような複数値は完全にスカラー化を返します。

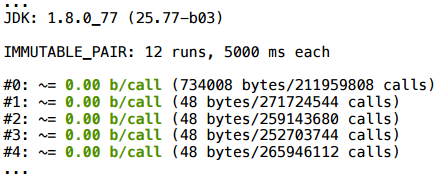
例3.1 値またはnull

例を少し変更してみましょう。状況によっては、nullを返します。







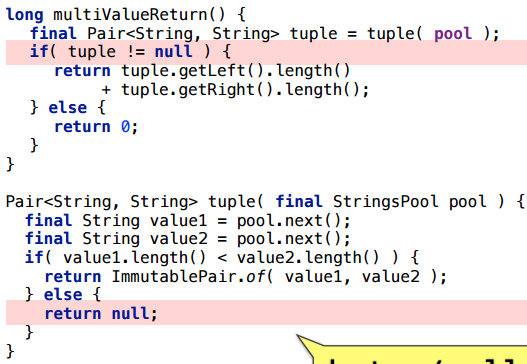
ご覧のとおり、割り当ては残ります（呼び出しごとの平均バイト数は整数ではありません。これは、nullを返すことがあるため、コストはかかりません）。

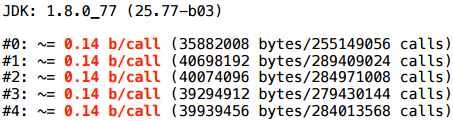
例3.2 混合型？

より複雑な例：Pairインターフェースと、このインターフェースの2つの実装があります。 人為的な条件に応じて、その実装または別の実装を返します。







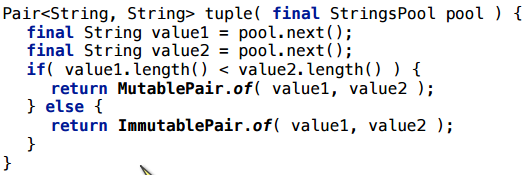
ここでも、割り当てのままです。







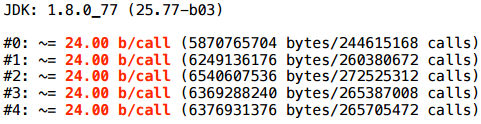
正直なところ、最初は異なるタイプであると確信していましたが、長い間信じていましたが、同じタイプでスカラーではない次の例を作成しました。











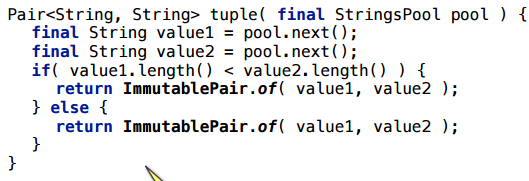
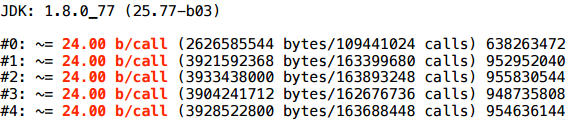
ここで何が起こっていますか？ さて、すべてのメソッドをペンでインライン化しようとすると、最初の実験のように、同じスクリプトにマージポイント（=リンクには2つの方法があります）が表示されます。

結論3：

シンプルに保つ：ブランチの数を減らす-エスケープ分析を混乱させにくい

例4.イテレーター

別の頻繁なパターンと非常に頻繁に表示される中間オブジェクト、その作成は避けたい。



これは、コレクションを反復処理する非常に単純なシナリオです。 コレクションを1回作成し、反復ごとに再作成するのではなく、反復子を再作成します。各メソッドの起動時に、反復子を介してコレクションを実行し、副作用を考慮します（コンパイラーがこの部分をスローしないようにするため）。





さまざまなコレクションに対してこのシナリオを検討してください。 まずArrayListについて考えましょう

例4.1 ArrayList.iterator

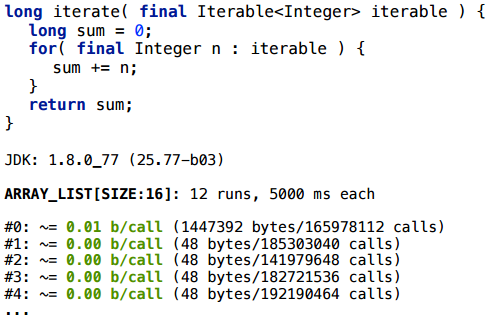
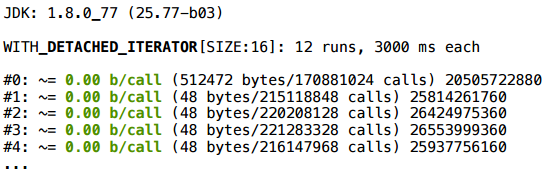
ArrayListの場合、反復子は実際にスカラー化されます（SIZEサイズは条件付きで取得されます：原則として、これは広範囲のSIZEに対して安定して機能します）。 LinkedListの場合、これも機能します。 長い間、すべてのオプションを検討することはしません。ここに、私が試したコレクションの要約表を示します。







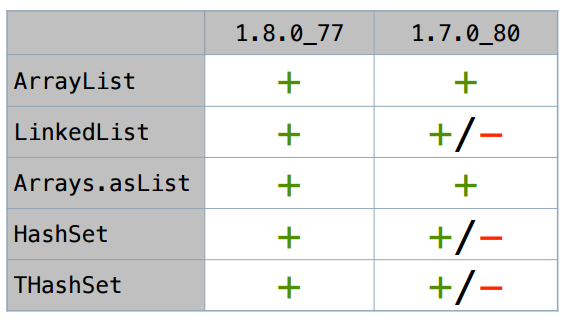
Java 8では、これらの反復子はすべて（少なくとも単純なスクリプトでは）スカラー化されます。

しかし、最新の更新では、Java 7の方が扱いにくいです。 それを詳しく見てみましょう（1.7はすでに廃止され、1.7.0_80が最後の更新であることを誰もが知っています）。



サイズが2のLinkedListの場合、すべてうまくいきます。







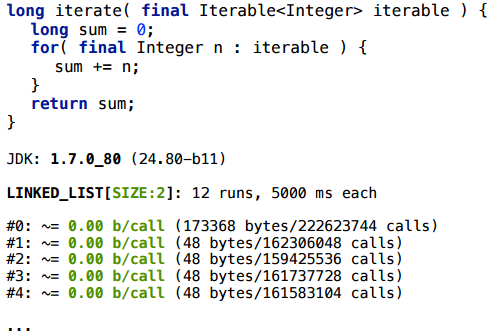
ただし、サイズが65のLinkedListの場合-いいえ。







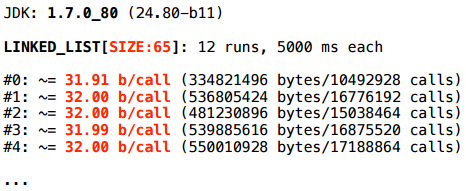
何が起こっているの？

マジックキーを取得し、サイズ2の場合、このようなインラインログの一部を取得します。







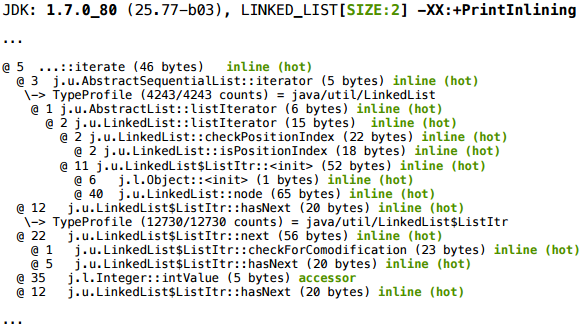
サイズ65の場合：







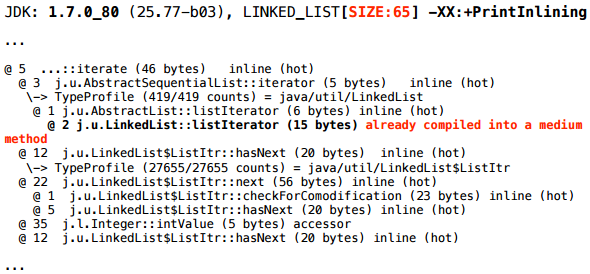
同じログの先頭に近いところに、このような画像の追加フラグメントがまだあります。







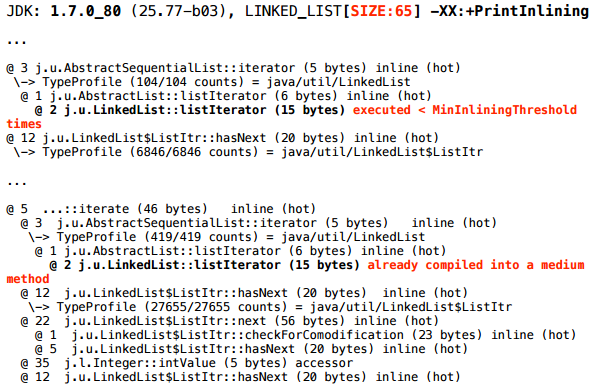
次のことが起こります。最初に、プロファイリングしているメソッドがコンパイルに行きました-JITがキューに入れました。 JITは非同期に動作します。つまり、 彼にはキューがあり、コンパイルタスクがそこにスローされ、別のスレッド（または複数のスレッド）で何らかのレートでキューからそれらを取り出してコンパイルします。 つまり、彼にタスクが与えられた瞬間と、新しいコードが最適化される瞬間の間に、しばらく時間がかかります。



そして今、私たちのiterate()



メソッドは初めてコンパイルに行きました。その間に、その中のLinkedList.listIterator()



メソッドがまだ実行されていないことが発見されました。 まだインライン化できていません（ MinInliningThreshold



= 250コール）。 しばらくして、 iterate()



呼び出しが再コンパイルに使用されたとき、 LinkedList.listIterator()



のコンパイルされた（マシン）コードLinkedList.listIterator()



大きすぎることがLinkedList.listIterator()



。



はい、診断の正確な意味：







つまり、 コンパイル済みのメソッドのサイズを推定するときは、バイトコードではなく、マシンコードを調べます（これはより適切なメトリックであるため）。 そして、これら2つのヒューリスティック-バイトコードとマシンコードの観点から-は必ずしも一貫していません。 5つのバイトコードのみのメソッドは、他のいくつかのメソッドを呼び出して貼り付け、マシンコードのサイズをしきい値よりも大きくすることができます。 この矛盾を根本的に解決することはできません。さまざまなヒューリスティックのしきい値を多少調整するだけで、平均してすべてがある程度良くなることを期待しています。



しきい値-特にInlineSmallCode-はバージョンによって異なります。 8には2倍のInlineSmallCodeがあるため、Java 8ではこのスクリプトは正常に機能します。メソッドはインラインで、イテレーターはスカラー化されますが、7ではそうではありません。



この例では、不安定であることが重要です。 コンパイルタスクがその順序で進むには（幸運なことに）はずです。 2回目の再コンパイルの時点でLinkedList.listIterator()



メソッドがまだ個別にコンパイルされていなかった場合、まだマシンコードはなく、バイトコードのサイズの基準に合格し、正常にインライン化されていました。 そのため、結果はリストのサイズに依存します。異なるメソッドがコンパイルに送信される速度は、ループ内の反復回数に依存します。



この仮説をテストできます。急流で遊ぶことです。 実際、それらをフィッティングすると、スカラー化が機能し始めます。

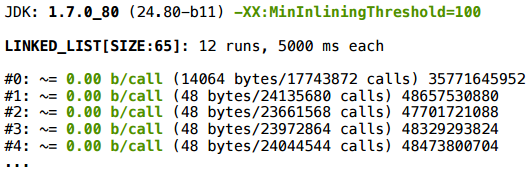
結論4：

• JVMの最初の鮮度は、最初の鮮度よりも優れています。
  
  
• -XX：+ PrintInlining-非常に優れた診断。スカラー化中に何が起こるかを理解できる主要な診断の1つ。
  
  
• 実際のデータでテストします-150を期待する場合、2のサイズでテストする必要はありません。150でテストすると、違いを見ることができます。
  
  
• ArrayListは再びLinkedListを設定します！
  
  

動的ランタイムはルーレットです。 JITコンパイルは非決定的であり、避けられません。 最近のバージョン（8-ke）では、ヒューリスティックのパラメーターは互いに若干調整されていますが、これは非決定性をキャンセルするものではなく、単にキャッチするのがより困難です。

例4.4 Arrays.asList（）

コレクションの別の興味深いバージョンがあります-配列のラッパー、Arrays.asList（）。 JITがそれをスカラー化するために、このラッパーが価値がないことを望みます。



ここではかなり奇妙なシナリオから始めます-配列からリストを作成し、インデックスを使用して、配列を通過するかのようにリストを調べます。







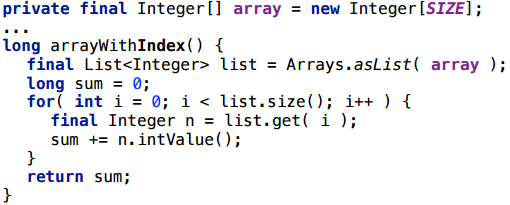
ここですべてが機能し、ラッパーの作成はスカラー化されます。







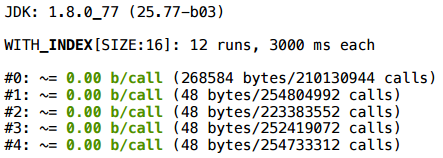
そして、イテレータに戻ります-配列のようにリスト内を移動できるように、配列をリストでラップすることはあまり意味がありません。







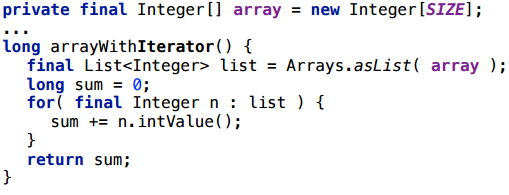
残念ながら、最新バージョンのJavaでも、割り当ては残っています。







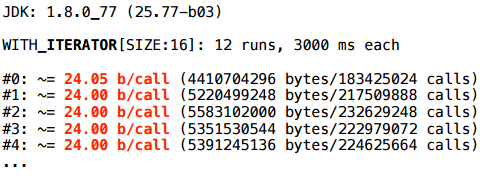
同時に、PrintInliningには特別なものは見当たりません。







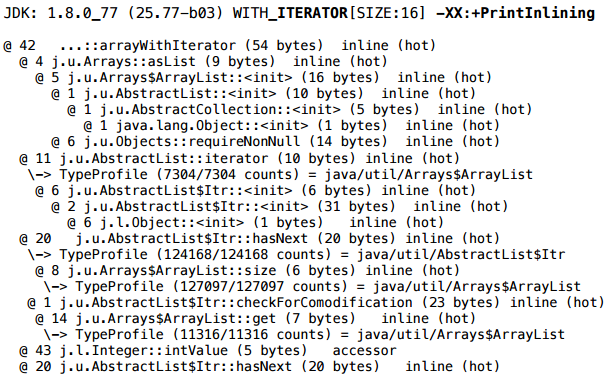
しかし、よく見ると、Arrays $ ArrayListのイテレータがそれ自体ではないことに注目してください。その実装はAbstractListから完全に継承されます。







そして、AbstractList $ Itrは、内部クラス、非静的内部クラスです。 そして、それが非静的であるという事実-何らかの理由でスカラー化を妨げます。 イテレータクラスを書き換える（つまり、Arrays $ ArrayListクラス全体をそれ自体にコピーして変更する）場合、イテレータを「アンティ」にします-イテレータに配列が渡され、イテレータにはリストオブジェクトへの参照が含まれなくなります-このシナリオでは、割り当てとしてスカラー化されますイテレータ、およびラッパー自体の割り当て$ ArrayList。











これはかなり不可解なケースであり、これはJITのバグのようですが、今日までのモラルは次のとおりです。ネストされたオブジェクトはスカラー化を混乱させます。

例4.4 コレクション*

そのようなシングルトンのコレクションがまだいくつかあり、それらのすべてとそのイテレータは、上記のArrays.asListを除き、Javaの現在および以前のバージョンで正常にスカラー化されています。

結論4.4。

ネストされたオブジェクトは非常にスケーラブルではありません。

• コレクションからのラッパーの反復。
  
  
• ... Arrays.asList（）を除く
  
  
• ネストされたオブジェクトはスカラー化されません（内部クラスを含む）。
  
  
• -XX：+ PrintInliningは引き続き問題を解決します。
  
  

例5.一定サイズの配列

可変サイズの配列（つまり、JITが予測できないサイズ）のスカラー化さえ望んでいないことをすぐに明確にします。 一定の長さの配列を使用します。

例5.1。 可変インデックス

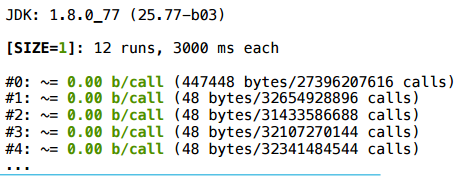
この例を考えてみましょう。配列を取得し、そこのセルに何かを書き込み、そこから何かを引きます。







サイズ1の場合、すべてが正常です。







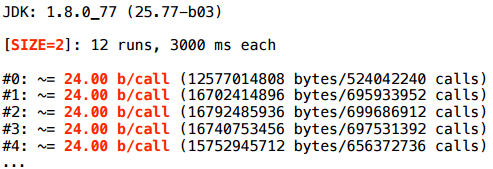
サイズ2では、何も起こりません。

例5.2。 定数インデックス

わずかに異なるアクセスを試してみましょう：同じサイズ2を取り、ハンドルで（展開）ループを展開するだけです-それを取得し、明示的なインデックスを見てください：







この場合、奇妙なことに、スカラー化が機能します。







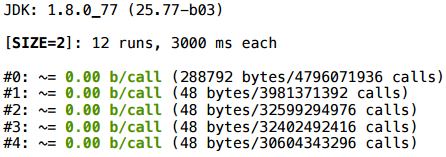
私は長い間議論しません-以下は要約版です。 手動で展開されたサイクルのこのケースは、サイズ64までスカラー化されます。ある種の変数インデックスがある場合、サイズ1と2は何らかの方法でスカラー化されますが、それ以上はスカラー化されません。







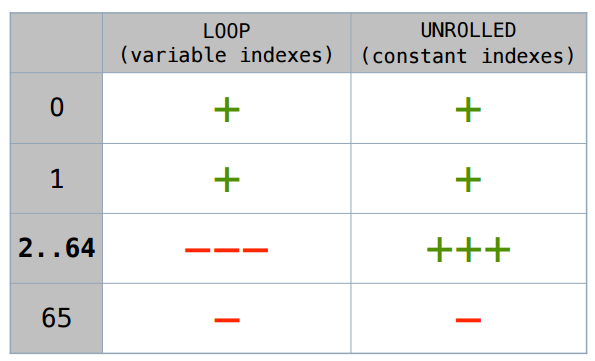
ブログの誰かが私に書いたように、JVMにはすべてのための独自のキーがあります。 この上限しきい値（-XX：EliminateAllocationArraySizeLimit = 64）も設定できますが、意味がないように思えます。 極端な場合、64個のローカル変数が追加されますが、これは多すぎます。

例5.3 プリミティブ配列

まったく同じコード、プリミティブ型の配列のみ-int、short ...







すべては、オブジェクトの場合とまったく同じ場合に機能します。







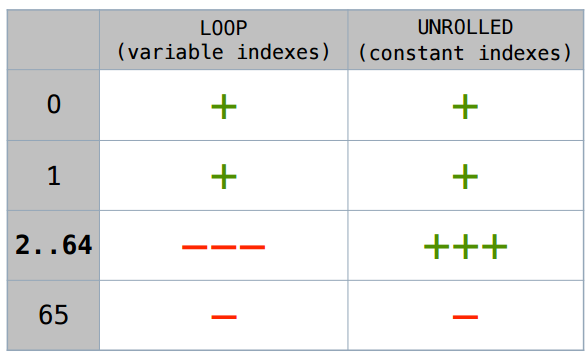
ループする配列をスカラー化できないのはなぜですか？ どのインデックスがiの後ろに隠れているかが明確ではないからです。 コードに配列[2]タイプがある場合、JITはこれを配列$ 2のローカル変数に変換できます。 そして、配列[i]を何に変えますか？ あなたは正確に何であるかを知る必要があります。 いくつかの特別な場合、短い配列の場合、JITはそれを「推測」できます。一般的な場合-いいえ。

例5.4 前提条件

guava , checkArguments(expression, errorMessageTemplate, args...)



, expression, expression == false. — vararg, , . , checkArguments



expressions == false, .

, expression . : vararg , expression false?







— 10 ^-7 :







.



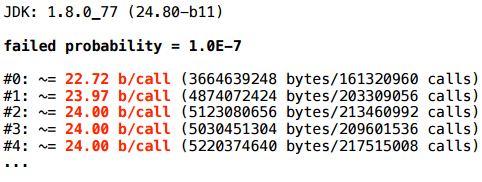
10 ^-9 , , , , - .







, - :





… .



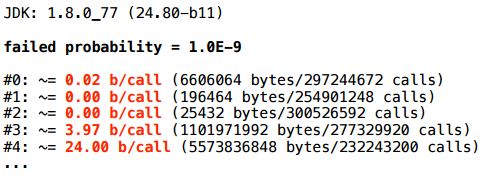
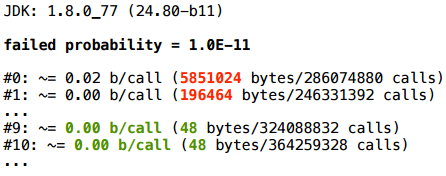
, — checkArguments, vararg — , , , expression false. checkArguments, expression false, - , - . , , , false , vararg , .

まとめ

• , ( );
  
  
• , (.. , , : - , );
  
  
• JVM .
  
  

: ( JVM). , , . . - , .



— :

• JVM;
  
  
• ( );
  
  
• ( , 1; 2-3 — , , , );
  
  
• ;
  
  
• null — ;
  
  
• — , , , ;
  
  
• .
  
  

---

– JPoint 2017 (7-8 ) JBreak 2017 (4 ) . , – , .