機械学習へのニューロベイズのアプローチ。 YandexでのDmitry Vetrovの講演

この投稿では、Data Festとの一連の講義を完了しています。 会議の中心的なイベントの1つは、HSEコンピュータサイエンス学部の教授であるDmitry Vetrovによる報告でした。 Dmitryはロシアで最も有名な機械学習の専門家の1人であり、昨年からYandexで主要な研究者として働いています。 レポートでは、ベイジアンアプローチの基本について説明し、ニューラルネットワークを使用する場合にこのアプローチが提供する利点について説明します。





カットの下-デコードとスライドの一部。

---

時間はあまりありません。トップに沿って走ります。 興味のある方はスライドを見ることができます-より厳密な結論があり、多くの美しく異なる式があります。 あまり退屈にならないことを期待しましょう。



何について話しますか。 ベイズの方法、確率論としてのベイズのアプローチ、機械学習の問題としての簡単な説明をしようとします。 このアプローチは、ディープニューラルネットワークの勝利の行列によって引き起こされた、90年代とゼロ年-ディープ革命が始まる前に非常に人気がありました。 しばらくの間、これらすべてのベイジアン手法が必要な理由は、ニューラルネットワークが非常にうまく機能しているように思えました。 しかし、よくあることですが、ある時点で、ニューラルネットワークとベイジアンアプローチの利点を組み合わせることができることがわかりました。 まず第一に、変分ベイズ推論の手法が登場し、これらのモデルは互いに矛盾せず、互いに完全に補完し、相互に補強し合っているという事実のためです。



ある意味で、私はこれを現代の機械学習と深層学習のさらなる発展の方向性と考えています。 ニューラルネットワークは万能薬ではないことを理解することが重要です。 それらは正しい方向への重要なステップにすぎませんが、最後のステップからはほど遠いものです。 機械学習の理論における次の可能なステップについてお話します。 そして、次の講演者であるセルゲイ・バルトゥノフは、神話の脱構築を試み 、ある意味で、ディープラーニングは万能薬ではないという考えを続けます。 しかし、Sergeyはこれに少し異なる視点からアプローチし、よりグローバルな視点を提供します。







それでは、ベイジアンアプローチとは何ですか？ 全体のアプローチは、単一の式または定理に基づいています。 ベイズの定理は、数学的および概念的な形式で与えられます。



重要なアイデア。 間接的な兆候のいくつかによって推定したい未知の量があると仮定します。 この場合、未知の量はθであり、その間接的な発現はyです。 次に、ベイズの定理を使用して、未知の量θの何らかの間接的な特徴を間接的に特徴付けるいくつかの間接的な特性を観察した後、未知の量の初期の無知または知識、事前知識を事後的に変換することができます。



式の重要な特徴は、未知の量に関する無知または不確実性をコード化する入力にアプリオリ分布を与え、その分布も出力であることです。 これは非常に重要なポイントです。 ポイントの推定値ではなく、入力時にあった同じ形式の何らかのエンティティ。 これにより、たとえば、ベイズ導出の結果である事後分布を、新しい確率モデルのアプリオリとして使用することが可能になり、そのため、さまざまな間接的な発現を分析することにより、異なる角度から新しい未知の量を特徴付けることができます。 これは、単純なモデルからより複雑なモデルを構築できる場合に、さまざまな確率モデルの拡張性または構成可能性の特性を取得できるための最初の利点です。



2番目の興味深いプロパティ。 確率の積を合計する最も単純なルールは、確率モデル、つまり、問題で発生するすべての変数の結合確率分布がある場合、少なくとも理論的には、常に確率的予測を構築し、関心のある変数を予測できることを意味します。 U、いくつかの観測可能な変数Oを知っています。さらに、変数Lがありますが、これは知らず、興味もありません。 この公式によれば、それらは考慮から完全に除外されます。



これらの3つの変数グループの任意の組み合わせについて、Oの値（おそらくUに関連する）を観察した場合、関心のある量に関するアイデアがどのように変化したかを示す条件付き分布をいつでも構築できます。







実際、ベイズの公式が広く使用されたことにより、確率論に対する2番目の代替アプローチが生まれました。 西側ではしばしばフリークエンシーと呼ばれる古典的なアプローチがあります-そして、別のベイジアンアプローチがあります。 これが私のすべての講義で提供する短い表であり、アプローチの違いを示しています。 当然、それらは互いに矛盾しません。 むしろお互いを補完します。 このプレートでは、共通点と相違点を確認できます。



主な違いは、ランダム変数の意味です。 頻度の用語では、統計変数を評価しないとその値を予測できない量としてのランダム変数を意味します。 客観的な不確実性を備えたものが必要ですが、ベイジアン手法では、ランダム変数は決定論的なプロセスとして単純に解釈されます。 完全に予測することができます。 この決定論的なプロセスでは、結果に影響するいくつかの要因がわからないというだけです。 私たちはそれらを知らないので、決定論的なプロセスの結果を予測することはできません。 したがって、私たちにとって、この結果はランダム変数のように見えます。



最も単純な例は、コインを投げることです。 これは古典的なランダム変数ですが、コインは古典力学の法則に従い、実際、すべての初期条件（力、加速、媒体の抗力係数など）を知っていることを理解しています。落ちます：ワシまたは尾。



考えてみると、ランダムと見なすために使用した量の大部分は、実際にはベイジアンの意味でランダムです。 これらはいくつかの決定的なプロセスであり、これらのプロセスの要因の一部はわかりません。



ある要因と他の要因を知らない場合があるため、主観的な不確実性または主観的な無知という概念が生じます。



残りはこの解釈の直接的な違いです。 ベイジアンアプローチのすべての値は、ランダムとして解釈できます。 確率論の装置は、ランダム変数の分布パラメーターに適用されます。 言い換えれば、古典的なアプローチでは無意味なことは、ベイジアンのアプローチでは意味があります。 最尤法の代わりに統計的手法-ベイズ定理。 ポイントではなく、異なる確率モデルを組み合わせることができる事後分布の形式の推定値を取得します。 そして、nが大きい場合に理論的に正当化される周波数アプローチとは異なり、たとえばnが無限に向かう傾向があることを証明するものとは異なり、ベイズのアプローチは、n = 0であっても任意のサンプルサイズに対して有効です。 。







シンプルなイラスト。 盲目の賢者と象の有名なたとえ話は、モデルがどのように引っ掛かるかを示しています。



想像してみてください：いくつかの盲目の賢者と1頭の象が与えられました。 タスクは、この象の質量を評価することです。 賢者は、今や何らかの動物を感じるようになることを知っています。 彼らはどれを知りませんが、質量を評価しなければなりません。







それらはすべて、動物の可能な質量についてのアイデアを先験的分布の形でエンコードすることから始まります。なぜなら、分布の密度が、何かに関する私たちの無知の単純な尺度を決定できるからです。 この知識をコード化するには、確率論の装置を使用するだけです。



私たちは賢者について話しているので、彼らは惑星地球上の動物の特徴的な質量を知っています。 したがって、彼らはそのような先験的な分布について理解します。



最初の賢者は彼の尾に近づき、彼の尾を感じ、明らかに彼の前に蛇のような何かまたは大きな動物の尾があると結論付けます。 したがって、ベイズ導出の過程で、p1の確率的区分として表現できる表現の結果を組み合わせることにより、条件x = 1の下で事後分布p（θ）を受け取ります。



次に、別の賢者が来ます。 これは完全に異なるモデルです。 X2は完全に異なる領域からの値であり、間接的に動物の質量を特徴づけます。 彼のベイジアン結論の過程で、彼はアプリオリ分布として、全員が始めた最初の分布ではなく、以前の賢者の結論の結果を使用します。 したがって、2つの完全に異なる次元、2つの情報源を1つのエレガントな確率モデルに組み合わせることができます。



したがって、一連の測定を行った後、最終的にはかなりシャープな事後分布、ほぼ正確な推定値を取得します。 動物がどれだけ持っていたかをすでに正確に言うことができます。 これは3番目の特性、つまり拡張性、つまりモデルが常に拡張および関与する能力の例です。



すでに機械学習に適用されているベイジアンアプローチのもう1つの利点は、正則化です。 先験的な設定を考慮することにより、機械学習の手順中にパラメーターのオーバーチューニングを防ぎ、再トレーニングの影響に対処することができます。 少し前、アルゴリズムが膨大な量のデータでトレーニングを開始したとき、再トレーニングの問題は議題から取り除かれたと考えられていました。 しかし、ポイントは、人々が巨大なニューラルネットワークに切り替えることを心理的に恐れているということだけでした。 それらはすべて小さなニューラルネットワークで始まり、巨大なトレーニングサンプルでは実際には再訓練されませんでした。 しかし、心理的な恐怖が消えると、人々はますます大きなネットワークを使用し始めました。



2つのことが明らかになりました。 まず、ネットワークが大きいほど良いです。 大規模なネットワークは、小規模なネットワークよりもうまく機能します。 しかし、大規模なネットワークは再訓練を始めています。 1億個のパラメーターがある場合、10億個のオブジェクトは非常に大きなトレーニングサンプルではないため、このような機械学習の手順を正規化する必要があります。



ベイジアンアプローチは、これらのパラメーターの事前分布、トレーニング手順中に構成されるニューラルネットワークの重みを導入することにより、これを行う絶好の機会を提供します。



特に、ドロップアウトなどの一般的なヒューリスティック正則化手法は特別なケースであり、ベイジアン正則化の大まかな近似であることが判明しました。 実際、これはベイジアンの結論を引き出す試みです。



最後に、3番目の利点は、潜在変数を使用してモデルを構築できることです。 彼女についての詳細。







やる気にさせる例があります-主成分法です。 この方法は非常に簡単です-線形次元削減。 高次元の空間でサンプルを取得し、共分散行列を作成し、対応する最大値を持つ主軸に投影します。 ここに幾何学的に示されているものがあります。 そして、サンプルに含まれる最大の分散を維持しながら、空間の次元を2から1に縮小しました。



この方法は簡単で、明示的に解決できます。 ただし、確率モデルの観点から、別の方法で定式化することもできます。







データが次のように編成されていると想像してください。各オブジェクトについて、小さな次元の空間に隠された表現があります。 ここでは、zとして示されています。 そして、高次元の空間でこの隠された表現の線形関数を観察します。 線形関数を取り、さらに通常のノイズを追加しました。 したがって、xの高次元データを取得しましたが、そこから低次元の表現を復元することが非常に望まれます。







数学的には、このように見えます。 確率モデルを定義しました。これは、xとzの観測されたコンポーネントと隠れたコンポーネントの同時確率分布です。 モデルは非常に単純で、サンプルはオブジェクトの積によって特徴付けられます。 各オブジェクトの観測されたコンポーネントは、非表示コンポーネントによって決定されます。非表示コンポーネントのアプリオリ分布について話しています。 どちらも正規分布です。 小さな空間では、データはアプリオリに正規分布していると仮定し、これらのデータの線形関数を観測します。



高次元表現を表すサンプルが与えられます。 私たちはxを知っており、zを知らず、私たちの仕事はパラメーターθを見つけることです。 θは行列V、σ²です。



示された問題は、潜在変数を持つ学習問題としてベイジアン言語で定式化できます。 通常の最尤法を適用するには、zの増加に関する知識が十分ではありません。 この手法には、EMアルゴリズムとさまざまな修正に基づく標準的なアプローチがあることがわかります。 反復プロセスを開始できます。 EMステップには、私たちが何をするかを記述する式があります。 理論的には、プロセスは単調であり、極値に収束することが保証されていますが、それでもまだです。



問題が発生します。問題が明示的に解決されていることがわかっているときに、反復プロセスを適用する必要があるのはなぜですか。



答えは簡単です。 はじめに-アルゴリズムの複雑さ。 分析ソリューションの複雑さはO（nD²）であり、EMアルゴリズムの1つの反復の複雑さはO（nDd）です。



100万次元の空間を10次元の空間に投影し、EMアルゴリズムが100の反復を収束すると想像すると、反復スキームは明示的な形式のソリューションよりも1000倍速く動作します。



さらに、重要な利点：私たちは基本モデルであり、主成分のメソッドであるため、特定のタスクの詳細に応じてさまざまな方法で拡張できます。 たとえば、主成分のメソッドの混合という概念を導入し、データは1つの空間、より小さな次元の線形部分空間ではなく、いくつかの空間に存在すると言うことができます。 そして、各部分空間からどの具象オブジェクトが来たかはわかりません。



主成分法の混合物が生じる。 正式には、モデルは次のように記述されます。 隠れた離散変数tの追加の命名法を導入しました。 繰り返しますが、EMアルゴリズムを使用すると、ほぼ同じ式を使用して問題の解決策を見つけることができますが、元の主成分の方法では変更を加えることができませんでした。







もう1つは、たとえば、サンプルでxの一部のコンポーネントが不明で、データが欠落している状況で機能することです。 それは起こりますか？ 非常に頻繁に。 ややエキゾチックな状況は、オブジェクトの一部の隠された表現、低次元表現、全体または一部を知っている場合です。 しかし、再び、そのような状況は可能です。

主成分法の初期モデルでは、どちらか一方を考慮することはできませんが、ベイジアン言語で定式化された確率モデルでは、EMアルゴリズムの簡単な変更によって両方を要素的に考慮します。 観測可能な隠れ変数の命名法をわずかに変更します。



したがって、このデータの任意のフラグメントが存在しない場合、標準の機械学習のように、観測可能な、つまり隠された、ターゲット変数の命名法が強調表示されており、混合できない場合のデータ処理の問題を解決できます。 これにより、柔軟性が向上します。







最後に、最近まで、ベイジアン手法の大きな制限は、計算の複雑さが高いため、小さなデータサンプルに適用でき、ビッグデータに転送できないことであると考えられていました。 過去数年間の結果は、そうではないことを示しています。 人類はついにベイジアン手法のスケーラビリティを提供することを学びました。 そして、人々はすぐにベイジアン手法とディープニューラルネットワークを交差させ始めました。



まだ時間がありますので、ベイジアン法をスケーリングする方法について少し説明します。







ベイズの定理。 有名なX、MについてZについて何か言いたいのですが、これはXと何らかの関係があります。ベイズの定理を適用します。 質問：ここで最も脆弱な場所は何ですか、最も重い紙は何ですか？ 不可欠。



積分が分析的に取られるまれなケースでは、すべてがうまくいきます。 分析的にとられない場合は別の問題です。しかし、高次元のデータについて話していると想像してください。ここでは、次元の空間の積分は1または2ではなく、数万および数十万です。



一方、チェーンを記録しましょう。 開始：∫p（X | Z）p（Z）dZ。 log P（X）dZは独立しているため、1に等しいZ全体の積分です。



2番目のアクション。 彼らは、この式に従ってp（X）を左に移動し、分母のp（Z | X）を積分の下に書きました。



現在、分子と分母はZに依存していますが、それらの商はp（X）を与えます。つまり、Zに依存しません。



次に、ログの下にあるものを乗算し、1を乗算し、q（Z）で除算します。



そして最後-積分を2つの部分に分けました。 ここでは、2番目の部分は確率理論でよく知られているカルバック・ライブラーの発散であり、これらの2つの分布が一致する場合にのみ、値は非負でゼロに等しくなります。 ある意味では、これは分布間の距離に類似しています。 そして、私はあなたに思い出させてください、私たちの仕事はベイズの結論を達成するために少なくともp（Z | X）を評価することです。



この値は計算できません。ここにp（Z | X）が表示されます。 しかし、最初の項は完全に計算できます。 各項はq（Z）に依存しますが、それらの合計はq（Z）に依存しません。logp（X）に等しいためです。 アイデアが生まれます：しかし、分布のq（Z）の最初の項を最大化します。



これは、最初の項を最大化することで、2番目の項を最小化することを意味します。これは、真の事後分布に対するq（Z）の近似の度合いを示します。 , , : , , .



.







. — .



, ? ? .



.







— . X _tr , Z , θ. , , L, θ — θ. L Q(Z) θ. θ , Q(Z) Z.



, . , , , . , , - .



, . , Z Q(Z). , . , .







, . , , , — , , .



. — . : . , , , . .



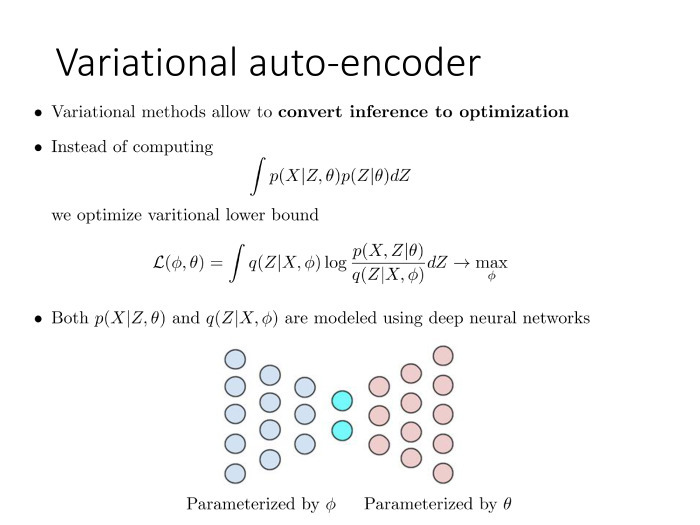
, , , - . , μ σ — . . , Z _i μ σ, X _i . θ. . , , .







, : , , . , . L, Q(Z), φ, . , , . , , — , .



. φ. , Z, X. — , X Z.



, . , .







, . , . , , , . representations.



log , , . , — , , , , — . — . - , , , , . . , , , , . .



, . — drop out. , , . , . , . . drop out , , , , .



, , attention maps, , . . , — L(Q|θ).



. , . , . , NIPS , , — .



, , , . — . ありがとう