🔺 📎 ♂️ 2つの機能があります。 ⛱️ ✖️ 🗄️

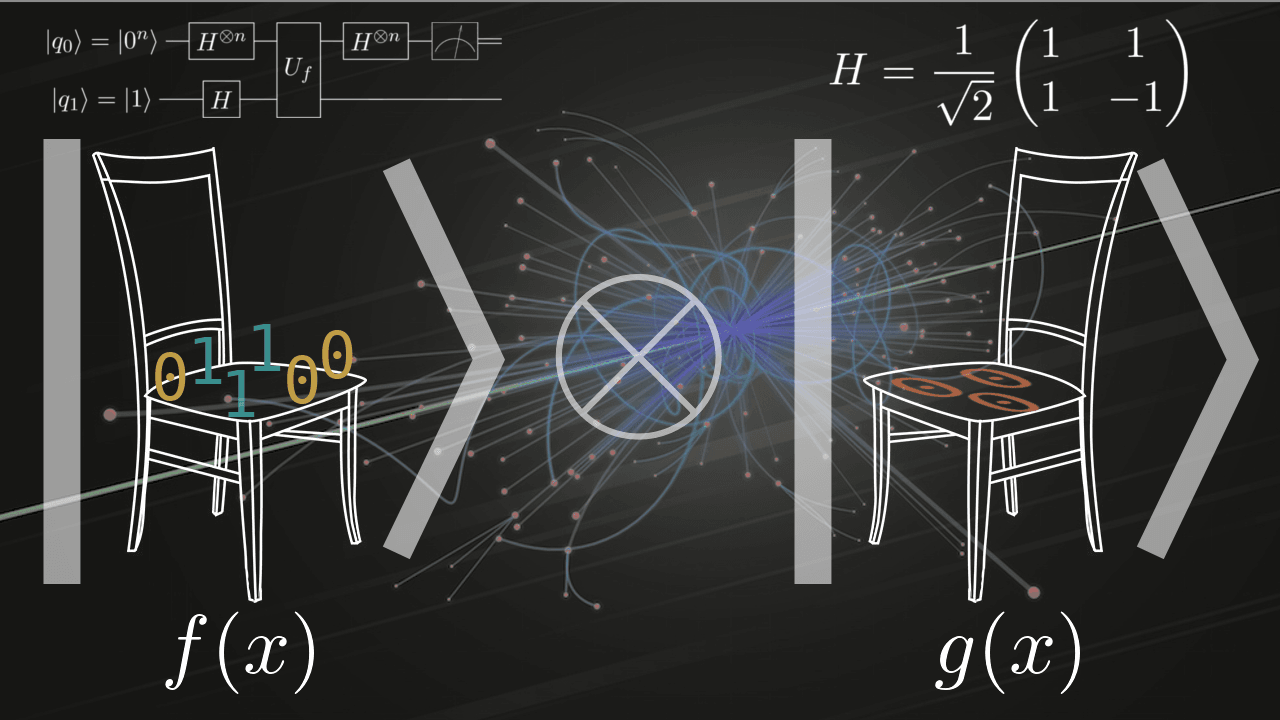
2つのブール関数があります $n$ 引数、1つは定数、もう1つはバランスが取れています。どちらに座り、どのフロントエンドに植えますか？ただし、関数は不明であり、一度だけ呼び出すことが許可されています。

この問題を解決する方法がわからない場合は、catにようこそ。そこで、量子アルゴリズムについて話し、最も一般的な言語であるPythonでそれらをエミュレートする方法を示します。

私はまたあなたと話しに来ました

2つの関数の問題をもう少し正式に設定してみましょう。ブール関数を与えてみましょう $f：\ {0、1 \} ^ n \から\ {0、1 \}$ そして、それは定数であることが先験的に知られています。つまり、その引数のいずれに対しても常に0または1を返すか、バランスが取れています。つまり、引数のちょうど半分が0を返し、正確に半分1を返します。またはバランス。さらに、関数が呼び出される時間は他の操作よりも計り知れないほど長いと考えられているため、アルゴリズムの複雑さは関数呼び出しの数によって決まります。

例：

$f（x_1、x_2）= x_1 \ oplus x_2$ バランスの取れた：

$x_1$	$x_2$	$f$
0	0	0
0	1	1
1	0	1
1	1	0

$f（x_1、x_2）= x_1 \ vee x_2 \ vee（\ネガx_1 \くさび\ネガx_2）$ 定数：

$x_1$	$x_2$	$f$
0	0	1
0	1	1
1	0	1
1	1	1

$f（x_1、x_2）= x_1 \くさびx_2$ バランスも一定もない：

$x_1$	$x_2$	$f$
0	0	0
0	1	0
1	0	0
1	1	1

もちろん、このタスクは人為的なものであり、実際に誰かが実際に会うことはまずありませんが、それは量子コンピューティングの勇敢な新しい世界への古典的なガイドであり、私はあえて伝統を破りません。

古典的な決定論的ソリューション

最初に、古典的な計算モデルの問題を解決しましょう。これを行うには、最悪の場合、次の関数を呼び出す必要があります。 $2 ^ {n-1} +1$ 引数：ちょうど半分ともう1つ。すべての計算値が同じ場合、関数は明らかに一定です。少なくとも2つの異なる結果が存在する場合、機能のバランスが取れています。決定論的アルゴリズムの複雑さは指数関数的であり、 $O（2 ^ {n-1} + 1）$ 。

Pythonアルゴリズム：

from itertools import product, starmap, tee def pairwise(xs): a, b = tee(xs) next(b, None) return zip(a, b) def is_constant(f, n): m = 2 ** (n - 1) for i, (x, y) in enumerate(pairwise(starmap(f, product({0, 1}, repeat=n)))): if i > m: break if x != y: return False return True

古典的な確率的ソリューション

しかし、引数の半分ではなく、より小さい数をチェックして判定に達した場合はどうでしょうか？正確な答えはもうありませんが、どのような確率で間違っていますか？関数を計算するとします $k＆lt; 2 ^ {n-1} + 1$ 引数。関数の値の中に2つの異なる値がある場合、すべてが単純です-関数のバランスが取れています。そうでなければ、確率で定数を宣言します $p（k）＆lt; 1$ 。私たちが間違っていて、機能が実際にバランスが取れていると仮定します。エラーの確率を計算します $1-p（k）$ 。引数を一様に選択した場合、関数の2つの連続した値が同じである確率は $1/2$ 、しかし会う確率 $k$ 同じ連続値は $1/2 ^ k$ 。このように：

$1-p（k）= \ frac {1} {2 ^ k}、$

$p（k）= 1-\ frac {1} {2 ^ k}。$

逆関数：

$k（p）= \ log_2 {\ frac {1} {1-p}}。$

固定で $p$ 古典的な確率的アルゴリズムの複雑さは一定であり、等しい $O（\ log_2 {\ frac {1} {1-p}）}。$ 99.99％の応答を確認するには、関数を14回だけ呼び出す必要があります。

Pythonアルゴリズム：

 import random from itertools import product, starmap, tee def pairwise(xs): a, b = tee(xs) next(b, None) return zip(a, b) def is_constant(f, n, k=14): xs = list(product({0, 1}, repeat=n)) random.shuffle(xs) xs = xs[:k] for x, y in pairwise(starmap(f, xs)): if x != y: return False return True

そして、複雑さを伴う一定の決定論的解決策があることを伝えた場合 $O（1）$ 関数を一度だけ呼び出すことができますか？

確かに、それを検討する前に、注意をそらす必要があります...

そっと忍び寄るビジョン

神話

開始する前に、量子コンピューティングに関連するいくつかの一般的な神話について説明します。

量子アルゴリズムは複雑です。

はい、それらは数学的想像力と洞察力を必要とするため、合成するのは困難です。それらを実際の量子コンピューターに実装することは困難です。そのためには、物理学に関する優れた知識を持ち、学科の研究室で毎日遅くまで起きている必要があります。しかし、間違いなく特別な知識と信じられないほどの勤勉を必要としないのは彼らの理解です。私は誰もが量子アルゴリズムを理解できることを確認します。彼らは、新入生が利用できる極めて単純な数学に頼っています。あなたに必要なのは、ほんの少し勉強する時間です。
D-Waveにはすでに数千の量子ビット量子コンピューターがあります

いいえ、これらは実際の量子コンピューターではありません。
実際の量子コンピューターはありません。

いいえ、存在します。実験室の条件では、数ビットしかありません。
量子コンピューターは、以前は利用できなかった問題を解決します

いいえ、古典モデルと量子モデルで計算可能な問題の多くは一致しています。量子コンピューティングは、これらのタスクの小さなサブセットの複雑さを減らすことしかできません。
量子コンピューターでは、Crysisは最高速度で飛行します

量子計算モデルが加速できるタスクのサブセットを除き、残りは古典的なコンピューターをエミュレートすることによってのみ解決できます。ご存知のように、これは非常に遅いです。クライシスは遅れる可能性があります。
量子コンピューターは、入力と出力を備えたブラックボックスであり、すべてを破壊することができます

あなたが12歳であれば、このアナロジーはそうでしょう。それ以外の場合、ボックス、ネコ、ループ、および「接続された」電子のストリングとの他のすべての類推のように、すべての一般的な科学ソースで積極的に促進され、混乱するだけで、誤解の錯覚を作成し、有用よりも有害です。これらのアナロジーを放棄します。

なんで？

なぜ応用数学者（プログラマー）は応用レベルで量子アルゴリズムを理解できるのでしょうか？ここではすべてが簡単です。次の2つの理由を説明します。

自己啓発のため。 どうして？
彼らはすでに来ています。 それらは量子コンピューターです。彼らはすでに近くにいます。サーバー会社にカップルが現れ、数年後にはラップトップのコプロセッサーとして点滅する時間はありません。そして、実行する場所はありません。量子コルーチンを呼び出すために、プログラムを作成する必要があります。そして、理解することなくそれを行うのは難しい、同意する。

寝ている間に種を残した

量子コンピューティングの最も基本的なコンポーネントは、量子システムです。 量子システムは物理システムであり、その動作はすべてプランク定数に匹敵します。この定義と、量子システムが行列力学の法則に従うという事実-私たちが物理学から必要とするすべての知識。次は数学のみです。

他の物理システムと同様に、量子システムは特定の状態になります。量子システムのすべての可能な状態はヒルベルト空間を形成します $\ mathcal {H}$ 複素数のフィールド上。読者が複素数の概念に精通していることを願っています-将来、どこでもそれらの理解が必要です。そうでない場合は、お会いして戻ってくることをお勧めします。ヒルベルト空間は、ノルムを持つ完全なノルム計量線形空間です $\ Vert x \ Vert = \ sqrt {（x、x）}$ どこで $（x、y）$ -スカラー積。最後から順に：

線形（ベクトル）スペース -多くの要素 $X$ 導入された要素を追加する操作 $x + y$ と乗算 $x \ cdot \ lambda$ フィールド要素ごと $K$ （この例では、複素数のフィールド）。これらの操作は閉じる必要があります（結果はセットに属している必要があります） $X$ ）および8つの公理が満たされなければなりません。完全なリストを参照すること、およびここで線形空間について詳しく知ることをお勧めします。
メートル空間で あらゆる要素に対して決定された距離要件を満たしている（メトリックの公理

スペース）：
- $\ rho（x、y）\ geqslant 0$ ながら $\ rho（x、y）= 0$ 場合にのみ $x$ そして $y$ 一致;
- $\ rho（x、y）= \ rho（y、x）$ ;
- $\ rho（x、y）\ leqslant \ rho（x、z）+ \ rho（z、y）$ -三角形の不等式。
正規化された空間で どんなアイテムでも実数があります、その規範と呼ばれ、再び満足のいく3つの公理：
- $\ Vert x \ Vert \ geqslant 0$ もし $\ Vert x \ Vert = 0$ それから $x = 0$ -ゼロ要素。
- $\ Vert \ lambda \ cdot x \ Vert = \ vert \ lambda \ vert \ cdot \ Vert x \ Vert$ ;
- $\ Vert x + y \ Vert \ leqslant \ Vert x \ Vert + \ Vert y \ Vert$ 。

結果空間にスカラー積の通常の要件を満たすスカラー積を導入し、上記のようにノルムを導入し、ヒルベルト空間を取得します。

また、 共役空間の概念についても説明します。に共役な空間 $\ mathcal {H}$ 呼ばれる空間 $\ mathcal {H ^ *}$ 上の線形演算子 $\ mathcal {H}$ 。線形演算子とは何ですか？線形関数の一般化と考えることができます：線形演算子の場合 $A：\ mathcal {H} \ to Y$ 実行する必要があります：

$A（\ lambda_1 x_1 + \ lambda_2 x_2）= \ lambda_1 A x_1 + \ lambda_2 A x_2、$

どこで $x_1、x_2 \ in \ mathcal {H}$ 、 $\ lambda_1、\ lambda_2 \ in K$ 。（実際、その標準は単一の超球に限定されるべきですが、より多くの面倒な定義を避けるために、そのような直感的なアイデアに自分自身を制限します。）

歴史的情報学では、歴史的な理由から、ディラックの表記法が使用されます。それらは不合理に面倒で気取らないように見えるかもしれませんが、遵守する価値のある標準です。この表記では、システムの状態を記述するヒルベルト空間の要素はketベクトルと呼ばれ、

$\左| \ psi \右\ rangle \ in \ mathcal {H}。$

ブラベクトルは共役空間の要素です

$\ langle \ left \ phi \ right | \ in \ mathcal {H ^ *}、$

そのような

つまり、線形演算子であり、その状態ベクトルへの適用は、「元の」ヒルベルト空間の対応する要素によるスカラー積に似ています。記録を簡単にするために、braベクトルをketベクトルに適用する場合、上の式に示すように、2本の垂直線が1本にマージされます。

ゼロ以外の定数による乗算のみが異なるベクトルが同じ物理状態に対応することが重要です。したがって、多くの場合、すべての可能な状態が考慮されるのではなく、正規化された状態、つまりそのようなサブセットのみが考慮されます $\ mathcal {H}$ あれ

$\ langle \ left \ psi | \ psi \右\ rangle = 1$

-各要素のノルムは1に等しい。このようなベクトルはすべて、単一の超球面上に存在します。

ヒルベルト状態空間で何らかの根拠を選択した場合 $\ {\左| e_i \ right \ rangle \} _ {i = 1} ^ m \サブセット\ mathcal {H}$ 、それから複素数のベクトルの形で任意のket-vectorを書くことができます-この基底に沿った展開の係数：

$\左| \ psi \ right \ rangle = \ sum_ {i = 1} ^ m {\ langle \ left e_i | \ psi \ right \ rangle \ left | e_i \ right \ rangle}、$

マトリックス力学は、膨張係数のモジュラスの平方 $\ vert \ langle \ left e_i | \ psi \ right \ rangle \ vert ^ 2$ この基準で測定されるとき、対応する基本状態で量子システムを見つける確率を物理的に意味します。

ここにあります- 量子システムの最初の主要な特性であり 、人気のある記事で頻繁に先延ばしにされています：システムを何らかの基準で測定すると、基本状態のいずれかになり、情報を失い、戻ることができません。読んだときに初めて、すべてが偶然に絶対に起こるという感覚が得られ、それに影響を与えることはできませんが、実際には、遷移確率は事前に知られており、さらに測定基準に依存しています。すべてが私たちが想像するほどランダムであれば、決定論的量子アルゴリズムは不可能でしょう。

ある固定基底のベクトルでヒルベルト空間の要素を表現できる場合、この空間上の線形演算子を行列で表現できます。

確かに

$A \左| \ psi \ right \ rangle = \ sum_ {i = 1} ^ m {\ langle \ left e_i | \ psi \ right \ rangle A \ left | e_i \ right \ rangle}$

同等に

$A \左| \ psi \ right \ rangle = \ hat {A} \ hat {\ psi}、$

どこで $\帽子{A}$ 演算子を交互に適用して得られた $A$ 基本的な要素に $\左| e_i \右\ラングル$ 結果の要素を行に書き込み、そして $\ hat {\ psi}$ -分解 $\左| \ psi \右\ラングル$ 同じ基準で。

演算子をしましょう $A$ 行列で表される

$A = \ begin {pmatrix} a_ {11}＆amp; a_ {12}＆amp; a_ {13}＆amp; \ドット＆アンプ; a_ {1m} \\ a_ {21}＆amp; a_ {22}＆amp; a_ {23}＆amp; \ドット＆アンプ; a_ {2m} \\ \ vdots＆amp; \ vdots＆amp; \ vdots＆amp; \ ddots＆amp; \ vdots \\ a_ {m1}＆amp; a_ {m2}＆amp; a_ {m3}＆amp; \ドット＆アンプ; a_ {mm} \ end {pmatrix}。$

行列の要素は複素数です。各要素を取り、それを複素共役（複素共役 $x + iy$ 番号と呼ばれる $x-iy$ ）同時に、マトリックス全体を転置します。

$A ^ \ダガー= \オーバーライン{A} ^ T = \ begin {pmatrix} \オーバーライン{a_ {11}}＆amp; \ {a_ {21}}とアンプに上線を引きます; \ {a_ {31}}＆amp;に上線を引きます\ドット＆アンプ; \上線{a_ {m1}} \\ \上線{a_ {12}}＆amp; \ {a_ {22}}とアンプ; \ {a_ {32}}とアンプ; \ドット＆アンプ; \上線{a_ {m2}} \\ \ vdots＆amp; \ vdots＆amp; \ vdots＆amp; \ ddots＆amp; \ vdots \\ \ {a_ {1m}}＆amp; \ {a_ {2m}}＆amp; \ {a_ {3m}}とamp; \ドット＆アンプ; \上線{a_ {mm}} \ end {pmatrix}。$

そのような行列 $A ^ \ダガー$ エルミート共役と呼ばれる $A$ 。もし $A A ^ \ dagger = A ^ \ dagger A = I$ どこで $私は$ （恒等行列を持つ）恒等演算子である場合、対応する演算子はunitaryと呼ばれます。

マトリックス力学が指示する2番目のルール ：単一の演算子のみが量子システムに作用できます。なんで？そのような変換は時間的に可逆であり、情報を失わないためです。確かに、

$U \左| \ psi_0 \ right \ rangle = \ left | \ psi_1 \右\ラングル、$

その後、逆変換を適用できます

$U ^ \ダガー\左| \ psi_1 \ right \ rangle = U ^ \ dagger U \ left | \ psi_0 \ right \ rangle = \ left | \ psi_0 \右\ラングル$

システムの初期状態を取得します。

最後に、最も重要なこと： テンソル積 。 2つのヒルベルト空間のテンソル積 $\ mathcal {H} _1$ そして $\ mathcal {H} _2$ ヒルベルト空間と呼ばれ、 $\ mathcal {H} _1 \ otimes \ mathcal {H} _2$ 。私は正式な定義を与えません。私たちにとって重要なプロパティにのみ注意します。

結果のスペースの次元は、ソーススペースの次元の積に等しくなります。

$\ dim {\ mathcal {H} _1 \ otimes \ mathcal {H} _2 $} = \ dim {\ mathcal {H} _1} \ cdot \ dim {\ mathcal {H} _2}$ ;
もし $\ {\左| e_i \ right \ rangle \} _ {i = 1} ^ m$ -基礎 $\ mathcal {H} _1$ 、そして $\ {\左| f_i \ right \ rangle \} _ {i = 1} ^ n$ -基礎 $\ mathcal {H} _2$ それから $\ {\左| e_i \ otimes f_j \ right \ rangle \} _ {i = 1、j = 1} ^ {m、n}$ -生成ベース $\ mathcal {H} _1 \ otimes \ mathcal {H} _2$ 。

演算子のテンソル積 $A$ から $\ mathcal {H} _1 ^ *$ そして $B$ から $\ mathcal {H} _2 ^ *$ （オペレーター $A$ 上記の行列で表されます）は演算子と呼ばれます $A \ otimes B$ から $\ big [\ mathcal {H} _1 \ otimes \ mathcal {H} _2 \ big] ^ *$ マトリックスあり

$A \ otimes B = \ begin {pmatrix} a_ {11} \ cdot B＆amp; a_ {12} \ cdot B＆amp; a_ {13} \ cdot B＆amp; \ドット＆アンプ; a_ {1m} \ cdot B \\ a_ {21} \ cdot B＆amp; a_ {22} \ cdot B＆amp; a_ {23} \ cdot B＆amp; \ドット＆アンプ; a_ {2m} \ cdot B \\ \ vdots＆amp; \ vdots＆amp; \ vdots＆amp; \ ddots＆amp; \ vdots \\ a_ {m1} \ cdot B＆amp; a_ {m2} \ cdot B＆amp; a_ {m3} \ cdot B＆amp; \ドット＆アンプ; a_ {mm} \ cdot B \ end {pmatrix}。$

このような積はクロネッカー積とも呼ばれます。2番目の行列に最初の行列の各要素を乗算し、結果のブロックからブロック行列を構成します。次元Aが等しい場合 $n_1 \回n_2$ 、次元Bは $m_1 \回m_2$ 、その後、テンソル積の過程で得られた行列の次元は $n_1 \ cdot m_1 \回n_2 \ cdot m_2$ 。

例：

$A = \ begin {bmatrix} 1＆amp; 2 \\ 3＆amp; 0 \ end {bmatrix}、\; B = \ begin {bmatrix} 1＆amp; 1 \\ 1＆amp; 2 \ end {bmatrix}、$

$A \ otimes B = \ begin {bmatrix} 1 \ cdot \ begin {pmatrix} 1＆amp; 1 \\ 1＆amp; 2 \ end {pmatrix}＆amp; 2 \ cdot \ begin {pmatrix} 1＆amp; 1 \\ 1＆amp; 2 \ end {pmatrix} \\ 3 \ cdot \ begin {pmatrix} 1＆amp; 1 \\ 1＆amp; 2 \ end {pmatrix}＆amp; 0 \ cdot \ begin {pmatrix} 1＆amp; 1 \\ 1＆amp; 2 \ end {pmatrix} \ end {bmatrix} = \ begin {bmatrix} 1＆amp; 1＆amp; 2＆amp; 2 \\ 1＆amp; 2＆amp; 2＆amp; 4 \\ 3＆amp; 3＆amp; 0＆amp; 0 \\ 3＆amp; 6＆amp; 0＆amp; 0 \\ \ end {bmatrix}。$

$A = \ begin {bmatrix} 1 \\ 0 \\ \ end {bmatrix}、\; B = \ begin {bmatrix} 1 \\ 2 \ end {bmatrix}、$

$A \ otimes B = \ begin {bmatrix} 1 \\ 2 \\ 0 \\ 0 \\ \ end {bmatrix}。$

量子システムの3番目の重要な特性 ：2つの量子システムは重ね合わせ状態になりますが、新しい状態空間は元の空間のテンソル積であり、新しいシステムの状態は元のシステムの状態のテンソル積になります。だから、状態のシステムの重ね合わせ $\左| \ psi \右\ rangle \ in \ mathcal {H} _1$ そして $\左| \ phi \右\ rangle \ in \ mathcal {H} _2$ 新しいシステムは可能になりますか $\左| \ psi \ right \ rangle \ otimes \ left | \ファイ\右\ラングル$ ヒルベルト空間によって記述される $\ mathcal {H} _1 \ otimes \ mathcal {H} _2$ 。

そして、私の脳に植え付けられたビジョン

それが私たちが必要とするすべての数学です。念のため、要約すると：

固定基底の場合、量子システムは複素ベクトルで記述でき、このシステムの進化はユニタリ複素行列で記述できます。
量子システムは任意の基底で測定でき、事前定義された確率に従って基底状態のいずれかになります。

古典的なコンピューターで量子アルゴリズムを記述、研究、理解、エミュレートするには、行列にベクトルを掛けるだけで十分です。これはニューラルネットワークよりも簡単です 。非線形性はありません！

キュービット

二次元ヒルベルト空間で記述された量子システムを見てみましょう $\ mathcal {H} ^ 2$ そして、その中でベクトルが $\左| 0 \右\ラングル$ そして $\左| 1 \右\ラングル$ 。括弧内には、2進数システムの基本ベクトルのインデックスが書き込まれ、追加の文字なしでゼロから始まります。このような指定は非常に便利です。このように

$\左| 0 \右\ rangle = \ begin {bmatrix} 1 \\ 0 \ end {bmatrix}、\; \左| 1 \ right \ rangle = \ begin {bmatrix} 0 \\ 1 \ end {bmatrix}、$

および任意のベクトル $\左| \ psi \右\ rangle \ in \ mathcal {H} ^ 2$ 次のように表現できます。

$\左| \ psi \ right \ rangle = \ alpha \ left | 0 \右\角+ +ベータ\左| 1 \右\ラングル、$

どこで $\アルファ$ そして $\ベータ$ そのようないくつかの複素数は $\ vert \ alpha \ vert ^ 2 + \ vert \ beta \ vert ^ 2 = 1$ （前の段落の展開係数と正規化条件の解釈を思い出してください）。そのため、このような単純な量子システムはキュービット （ quanti bit 、 qbit ）と呼ばれます。量子ビットは、量子コンピューティングモデルの古典的なビットに類似しています。 1つの量子ビットのさまざまな状態の空間が $\ mathcal {H} ^ 2$ ブロッホ球と呼ばれる三次元球で、ここで $\左| 0 \右\ラングル$ 下の極に対応し、 $\左| 1 \右\ラングル$ -トップへ。

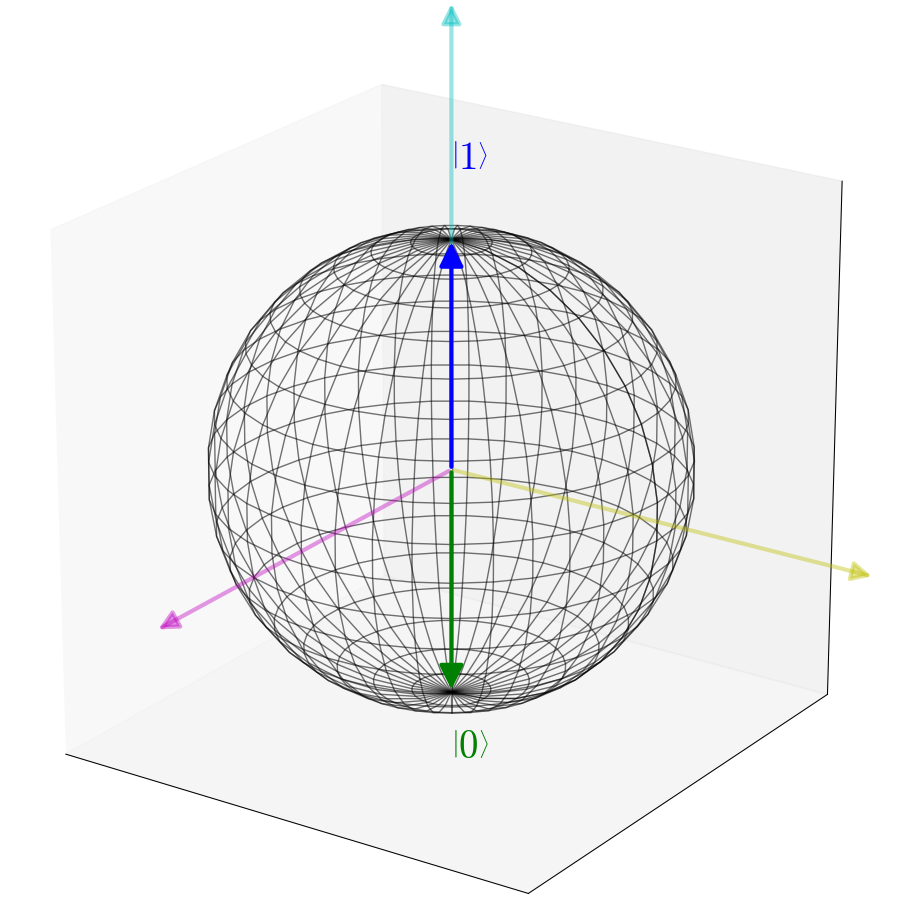
登録する

1ビットは1ビットのように退屈すぎるので、すぐに複数のキュービットの重ね合わせを検討してください。このような重ね合わせは、 量子レジスター （ qregister ）と呼ばれます。 $n$ 量子ビット。たとえば、2量子ビットの量子レジスタは空間で記述されます $\ mathcal {H} ^ 4$ 4つの基本的な状態があります。

$\左| 00 \ right \ rangle = \ left | 0 \ right \ rangle \ otimes \ left | 0 \ right \ rangle = \ begin {bmatrix} 1 \\ 0 \\ 0 \\ 0 \ end {bmatrix}、$

$\左| 01 \ right \ rangle = \ left | 0 \ right \ rangle \ otimes \ left | 1 \ right \ rangle = \ begin {bmatrix} 0 \\ 1 \\ 0 \\ 0 \ end {bmatrix}、$

$\左| 10 \右\角= =左| 1 \ right \ rangle \ otimes \ left | 0 \ right \ rangle = \ begin {bmatrix} 0 \\ 0 \\ 1 \\ 0 \ end {bmatrix}、$

$\左| 11 \ right \ rangle = \ left | 1 \ right \ rangle \ otimes \ left | 1 \ right \ rangle = \ begin {bmatrix} 0 \\ 0 \\ 0 \\ 1 \ end {bmatrix}。$

したがって、そのようなレジスタの状態 $\左| \ phi \ right \ rangle \ in \ mathcal {H} ^ 4$ として表すことができます

どこで $\ vert \ alpha_1 \ vert ^ 2 + \ vert \ alpha_2 \ vert ^ 2 + \ vert \ alpha_3 \ vert ^ 2 + \ vert \ alpha_4 \ vert ^ 2 = 1$ 。表記では、単位がオンの基底ベクトル $k$ -th位は数字で示されます $k$ バイナリ形式で書かれています。

さらに同様。からの量子レジスタ $m$ 量子ビットについて説明します $2 ^ m$ 次元ヒルベルト空間 $\ mathcal {H} ^ {2 ^ m}$ 持っている $2 ^ m$ 同様の方法で形成された基底状態。長時間遅延することなく、量子レジスタをエミュレートする方法を学習します。

 import numpy as np class QRegister: def __init__(self, n_qbits, init): self._n = n_qbits assert len(init) == self._n self._data = np.zeros((2 ** self._n), dtype=np.complex64) self._data[int('0b' + init, 2)] = 1

量子レジスタを作成するための3行のコード-まったく難しくありません。同意します。次のように使用できます。

 a = QRegister(1, '0') # |0> b = QRegister(1, '1') # |1> c = QRegister(3, '010') # |010>

量子アルゴリズムには以下が含まれます。

量子レジスターの初期化。
その上のユニタリ変換のセット。
結果の測定。

計測

最初のポイントを見つけて、それをエミュレートする方法を学びました。最後のポイントである測定をエミュレートする方法を学びましょう。覚えているように、状態ベクトルの係数の2乗は、この状態への遷移の確率を物理的に意味します。これに従って、QRegisterクラスに新しいメソッドを実装します。

 def measure(self): probs = np.real(self._data) ** 2 + np.imag(self._data) ** 2 states = np.arange(2 ** self._n) mstate = np.random.choice(states, size=1, p=probs)[0] return f'{mstate:>0{self._n}b}'

次のいずれかを選択する確率の確率を生成します $2 ^ n$ 状態を状態化し、 np.random.choice

を使用してランダムに選択します。残っているのは、対応するパディングゼロの数を持つバイナリ文字列を返すことだけです。明らかに、基本的な状態の場合、答えは常にこの状態自体と同じで等しくなります。チェック：

 >>> QRegister(1, '0').measure() '0' >>> QRegister(2, '10').measure() '10' >>> QRegister(8, '01001101').measure() '01001101'

ほとんどすべてが問題を解決する準備ができています！量子レジスタに影響を与える方法を学ぶことだけが残っています。ユニタリ変換によってこれができることはすでにわかっています。量子情報学では、ユニタリ変換はゲートと呼ばれます（ 量子ゲート 、 qgate 、 ゲート ）。

ゲイツ

この記事では、私たちにとって有用な最も基本的なゲートのごく一部を検討します。実際、もっとたくさんあります。

シングル

検討するのが最も簡単なのは、単一のゲートです。その行列は次のとおりです。

$I = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}.$

影響するキュービットは変更しません。

しかし、それは役に立たないと考えないでください-私たちはそれを必要とします、そして複数回。

ゲートアダマール

$H = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix}$

マトリックスがユニタリであることを確認することは難しくありません。

$H H^\dagger = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \cdot \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix} = I.$

基本的なキュービットに対するアダマールゲートの動作を考えます。

$H \left| 0 \right\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1\\ 0 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1\\ 1 \end{bmatrix} = \frac{1}{\sqrt{2}} (\left| 0 \right\rangle + \left| 1 \right\rangle),$

$H \left| 1 \right\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \begin{bmatrix} 0\\ 1 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1\\ -1 \end{bmatrix} = \frac{1}{\sqrt{2}} (\left| 0 \right\rangle - \left| 1 \right\rangle).$

または、一般的な形式[1]：

$H \left| x \right\rangle = \frac{1}{\sqrt{2}} \sum_{y \in \lbrace 0,1 \rbrace} (-1)^{x \cdot y} \left| y \right\rangle.$

ご覧のように、アダマールゲートは基本的な状態を同等の確率に変換します。等しい確率で測定すると、任意の結果を得ることができます。

ゲイツパウリ

Wolfgang Pauliによって導入された行列が対応する3つの重要なゲート：

$X = \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix},\; Y = \begin{bmatrix} 0 & -i\\ i & 0 \end{bmatrix},\; Z = \begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix}.$

ゲートは $X$ NOT ゲートとも呼ばれます。

$X \left| 0 \right\rangle = \left| 1 \right\rangle, \; X \left| 1 \right\rangle = \left| 0 \right\rangle,$

幾何学的にその適用は $\ pi$ 、軸を中心にラジアンでブロッホ球をオンにすることと同等です $x$ 。

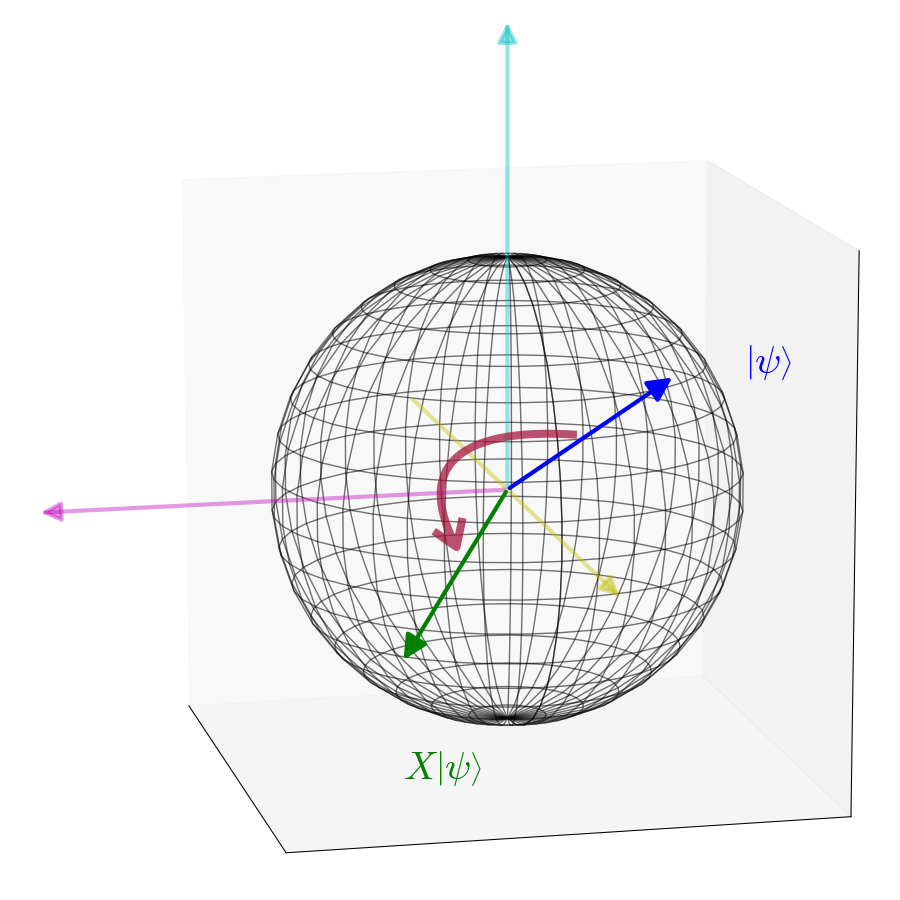
ゲイツ $Y$ そして $Z$ ゲートに似てい $X$ ますが、対応する軸を中心に回転する点が異なります。

ゲートを使用する定理があります $私は$ 、 $X$ 、 $Y$ そして $Z$ 任意の単一キュービットゲートを表現できます。例：

$H = \frac{1}{\sqrt{2}}\big(X + Z\big),$

アダマールゲートは幾何学的に $\ pi$ 軸を中心としたラジアンによる回転を意味することがわかります $\frac{x + z}{\sqrt{2}}$ 。

考慮されるすべてのゲートをPythonに実装します。これを行うには、別のクラスを作成します。

 class QGate: def __init__(self, matrix): self._data = np.array(matrix, dtype=np.complex64) assert len(self._data.shape) == 2 assert self._data.shape[0] == self._data.shape[1] self._n = np.log2(self._data.shape[0]) assert self._n.is_integer() self._n = int(self._n)

そして、クラスQRegister

にゲートを適用する操作を追加します。

 def apply(self, gate): assert isinstance(gate, QGate) assert self._n == gate._n self._data = gate._data @ self._data

そして、すでにわかっているゲートを作成します。

 I = QGate([[1, 0], [0, 1]]) H = QGate(np.array([[1, 1], [1, -1]]) / np.sqrt(2)) X = QGate([[0, 1], [1, 0]]) Y = QGate([[0, -1j], [1j, 0]]) Z = QGate([[1, 0], [0, -1]])

イーグルまたは尾？

簡単な量子アルゴリズムの例を見てみましょう。ランダムビットを生成します-ゼロまたは1、ワシ、または尾。これは宇宙で最も正直なコインになります-結果は測定された場合にのみ知られ、偶然の性質は宇宙のまさしくその基礎に縫い込まれ、いかなる方法でもそれに影響を与えることは不可能です。

アルゴリズムには、1つのキュービットのみが必要です。最初の瞬間の状態にする $\left| 0 \right\rangle$ ：

$\left| 0 \right\rangle = \begin{bmatrix} 1\\ 0 \end{bmatrix}.$

アダマールゲートを適用し $H$ て状態を取得します

$H \left| 0 \right\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 1\\ 1 \end{bmatrix}.$

結果のシステムを測定する場合 $\Big\vert \frac{1}{\sqrt{2}} \Big\vert^2 = \frac{1}{2}$ 、状態にある可能性が高く $\left| 0 \right\rangle$ 、状態にある確率はまったく同じです $\left| 1 \right\rangle$ 。結果を記録するためだけに残ります。

古典的なコンピューターでエミュレートするアルゴリズムを確認しましょう。

 from quantum import QRegister, H def quantum_randbit(): a = QRegister(1, '0') a.apply(H) return a.measure() for i in range(32): print(quantum_randbit(), end='') print()

結果：

 ➜ python example-randbit.py 11110011101010111010011100000111 ➜ python example-randbit.py 01110000111100011000101010100011 ➜ python example-randbit.py 11111110011000001101010000100000

上記のアルゴリズム全体は、1組の式で記述できます。

ただし、このようなレコードを扱うのはあまり便利ではありません。リスト構造（古典的なアルゴリズムに適した一連のアクション）は、量子の場合には適用できません。ここでは、サイクルも条件もなく、。したがって、量子回路は、量子コンピューター科学のアルゴリズムを記述するために広く使用されています。上記のアルゴリズムの図は次のとおりです。

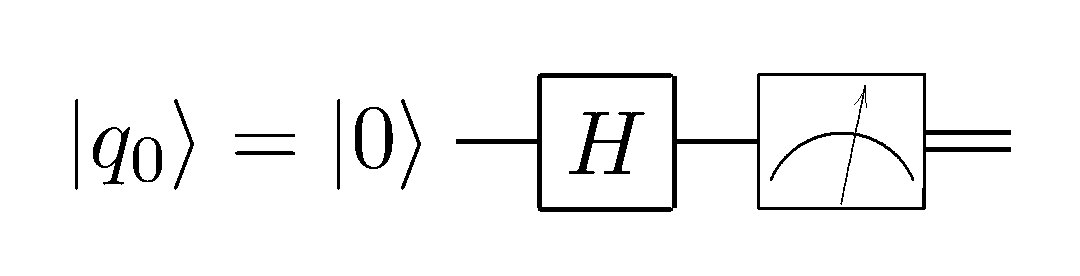
左側には、システムの初期状態が常に表示されます。長方形は、この状態で実行されたユニタリ変換を示し、最後に、測定デバイスのアイコン（測定操作）がすべてまたはいくつかのキュービットにあります。ドット、ブランチ、円の形のいくつかのマルチキュービット変換には「構文糖」もあります。それだけです。正方形を三角形や円と区別できれば、量子アルゴリズムのスキームを簡単に理解できます。

量子ビットの神へのより多くの量子ビット

しかし、1つのキュービットではなく、レジスタ全体で作業するとどうなりますか？そして、1つのキュービットのみにゲートを適用するとしますか？テンソル製品の特性が助けになります。演算子のテンソル積の定義により $A: V \to W$ そして $B: X \to Y$ ：

$(A \otimes B)(v \otimes x) = Av \otimes Bx,$

どこで $v \in V$ 、 $Xのx \$ 。次に：

$(A \otimes I)(v \otimes x) = Av \otimes Ix = Av \otimes x,$

つまり、ゲートを1つのキュービットに適用し、それを2つ目のキュービットに接続して量子レジスタを取得するか、演算子をレジスタ全体に適用するかは問題ではありません。 $A \otimes I$ 。同様 $A$ に、2番目のキュービットにのみ演算子を適用する場合は、レジスタ全体に演算子を適用できます $I \otimes A$ 。これは、そのようなスキームが次のことを意味します。

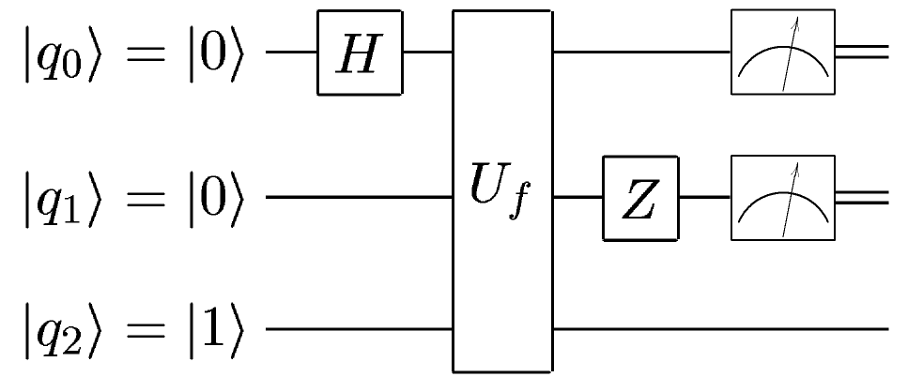
これに完全に似ています：

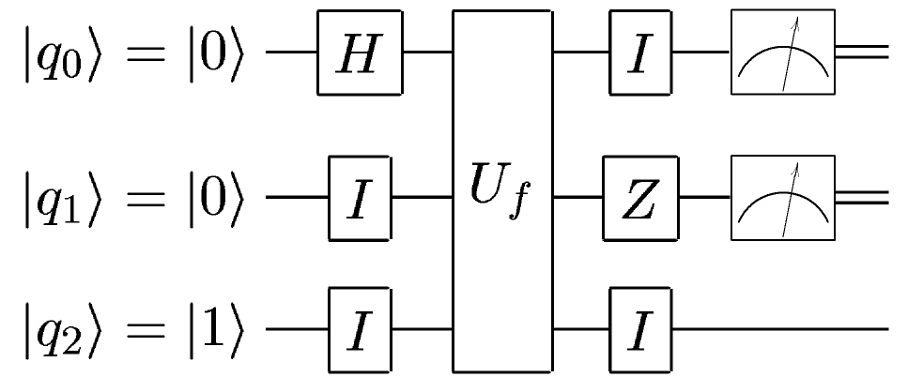
便宜上、単一のゲートのみが省略されています。

そして、逆に、一度に複数のキュービットにゲートを適用したい場合はどうでしょうか？繰り返しになりますが、テンソル積の定義から、このためにこのゲートを適用することができます。必要な回数だけテンソルを乗算します。

$Hv \otimes Hx = (H \otimes H) (v \otimes x) = H^{\otimes2} (v \otimes x).$

$A^{\otimes n}$ テンソルべき乗を意味します。ちなみに $\left| \psi \right \rangle^{\otimes n}$ 簡潔にするために、 $\left| \psi^n \right \rangle$ 。このように

$H^{\otimes n} \left| 0^n \right \rangle$

意味： $n$ ゼロ量子ビットの量子レジスタの各量子ビットにアダマール変換を適用します。

にテンソル積とべき乗を追加しますQGate

。

 def __matmul__(self, other): return QGate(np.kron(self._data, other._data)) def __pow__(self, n, modulo=None): x = self._data.copy() for _ in range(n - 1): x = np.kron(x, self._data) return QGate(x)

量子神託

各バイナリ関数は、 $f : \{0, 1\}^n \to \{0, 1\}$ 唯一mnogokubitnyゲート寸法対応 $n + 1$ で示され、 $U_f$ そして呼ばれる量子オラクルこの機能のために。関数に関するすべての情報が含まれており、 $f$ すべての可能な引数で同時に呼び出すことができます。

なぜその次元 $n + 1$ ？問題は、量子コンピューティングの別の基本的な特性によれば、情報は失われず、時間的に可逆であるということです。古典的な計算モデルで関数を呼び出して $f(x, y) = x \oplus y$ 結果を取得した場合、その関数がどの引数で呼び出されたかを判断できないため、時間内に計算を元に戻すことはできません。

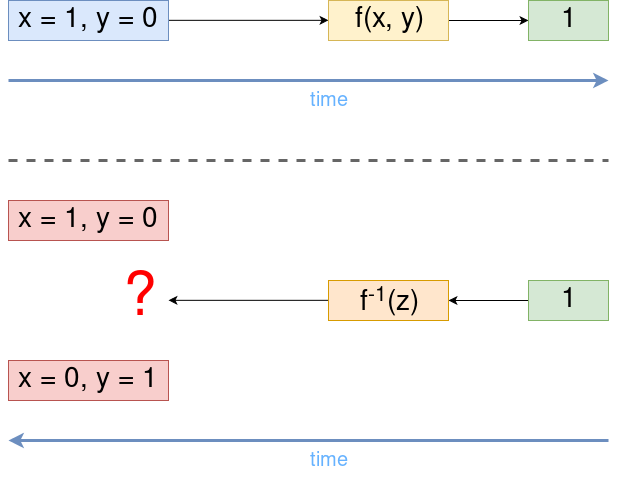
これを回避する1つの方法は、関数が呼び出された引数を記憶することです。

コンピューティングの量子モデルでも同じことが起こりますが、それがまさにその性質に組み込まれているだけです。完全な情報を保存せずに、単一の変換を構築することは不可能です。

量子オラクルは $U_f$ 、状態 $\left| x \right \rangle \left| y \right \rangle$ を状態に移行する単一変換として定義されます $\left| x \right \rangle \left| y \oplus f(x) \right \rangle$ どこで $n$ マークされた量子ビットは $x$ 、関数の引数に関する情報を保持し、変更されないままで、唯一の量子ビット $y$ はその結果です。 $\oplus$ 2を法とする加算を

示します。例を見てみましょう。1つの引数の関数に対してOracleを構築したいとしましょう $f(x) = x$ 。したがって、対応する演算子 $U_f$ は2キュービットであり、次元の正方行列で記述できます $2^2 = 4$ 。上記の規則に従って、可能なすべての基本的なレジスターの状態がどの状態になるかを調べます。

ユニット行列演算子は、 $私は$ i番目の行で行列を乗算するとき $私は$ に、ベクトルのi番目のコンポーネントを取得して同じ場所に配置するため、状態をそれ自体に取り込みます。 $私は$ i番目の行の行列で、i番目以外のすべての要素 $j$ がゼロで1である場合 $j$ 、結果のベクトルの $私は$ 代わりに、元のベクトルのth番目にあった要素を置きます。上記の例では、そのままにする必要があります ${00}_2 = 0$ そして ${01}_2 = 1$ 状態ベクトル要素とスワップ ${10}_2 = 3$ そして ${11}_2 = 4$ 要素。それから $U_f$ 次のようになります。

$U_f = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ \end{bmatrix}.$

チェック：

$\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ \end{bmatrix}\begin{bmatrix} x_{00} \\ x_{01} \\ x_{10} \\ x_{11} \\ \end{bmatrix} = \begin{bmatrix} x_{00} \\ x_{01} \\ x_{11} \\ x_{10} \\ \end{bmatrix}.$

同様に、他の関数の場合、任意の数の引数。実装します：

 def U(f, n): m = n + 1 U = np.zeros((2**m, 2**m), dtype=np.complex64) def bin2int(xs): r = 0 for i, x in enumerate(reversed(xs)): r += x * 2 ** i return r for xs in product({0, 1}, repeat=m): x = xs[:~0] y = xs[~0] z = y ^ f(*x) instate = bin2int(xs) outstate = bin2int(list(x) + [z]) U[instate, outstate] = 1 return QGate(U)

まだ残っている

さて、問題を解決するために必要なすべての基礎を調べ、このソリューションの検証に役立つ小さなpythonフレームワークを作成することさえできました。1つの関数呼び出しで関数が定数か平衡かを判断できるアルゴリズムは、Deutsch-Jojiアルゴリズムと呼ばれます。1つの変数の関数のアルゴリズムのバージョンは、1985年にDavid Deutschによって開発され、1992年にRichard Yogiの助けを借りていくつかの変数のケースに一般化されました。このアルゴリズムの図は次のとおりです。

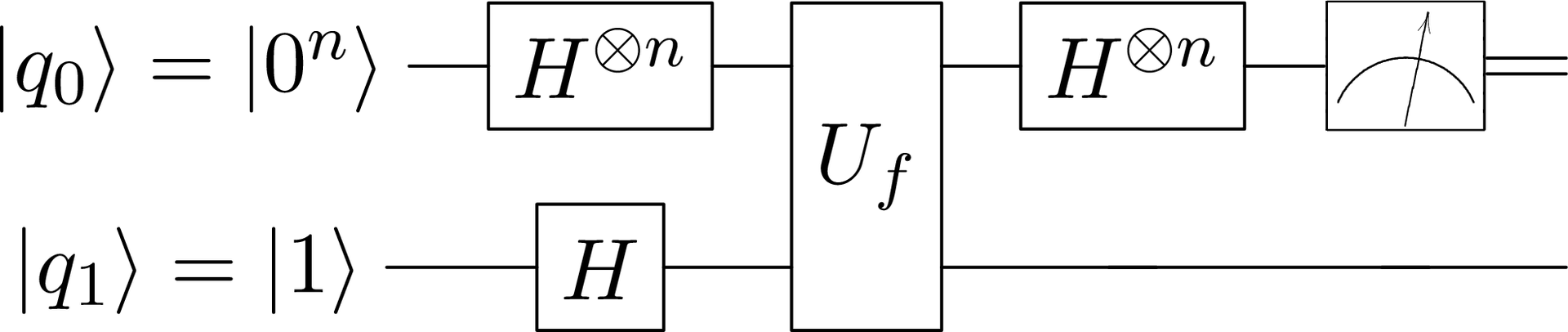
測定結果が0の場合、関数は一定です。それ以外の場合はバランスがとれています。アルゴリズムをすぐに実装します。

 from quantum import QRegister, H, I, U def is_constant(f, n): q = QRegister(n + 1, '0' * n + '1') q.apply(H ** (n + 1)) q.apply(U(f, n)) q.apply(H ** n @ I) if q.measure()[:~0] == '0' * n: return True else: return False

そしてチェック：

 def f1(x): return x def f2(x): return 1 def f3(x, y): return x ^ y def f4(x, y, z): return 0 print('f(x) = x is {}'.format('constant' if is_constant(f1, 1) else 'balansed')) print('f(x) = 1 is {}'.format('constant' if is_constant(f2, 1) else 'balansed')) print('f(x, y) = x ^ y is {}'.format('constant' if is_constant(f3, 2) else 'balansed')) print('f(x, y, z) = 0 is {}'.format('constant' if is_constant(f4, 3) else 'balansed'))

結果：

 f(x) = x is balansed f(x) = 1 is constant f(x, y) = x ^ y is balansed f(x, y, z) = 0 is constant

動作します。いいねなぜ機能するのですか？アルゴリズムの正しさを証明すると同時に、その動作原理を見てみましょう。任意の基本状態の量子レジスター

に対するゲートの動作を考えてみましょう $H$ [1]：

$H^{\otimes n} \left|x_1, x_2, \ldots, x_n\right\rangle =$

（テンソル積の特性による）

$= H \left| x_1 \right\rangle \otimes H \left| x_2 \right\rangle \otimes \dots \otimes H \left| x_n \right\rangle =$

（個々のキュービットに適用可能）

$=\frac{1}{\sqrt{2^n}} \Big(\sum \limits_{y_1 \in \lbrace 0,1 \rbrace} (-1)^{x_1 \cdot y_1} \left| y_1 \right\rangle \otimes \sum \limits_{y_2 \in \lbrace 0,1 \rbrace} (-1)^{x_2 \cdot y_2} \left| y_2 \right\rangle \otimes \ldots \otimes \sum \limits_{y_n \in \lbrace 0,1 \rbrace} (-1)^{x_n \cdot y_n} \left| y_n \right\rangle \Big) =$

（テンソル積の符号として-1を取ります）

$=\frac{1}{\sqrt{2^n}} \sum \limits_{(y_1, y_2, \ldots, y_n) \in \lbrace 0,1 \rbrace^n} (-1)^{x_1 \cdot y_1 \oplus x_2 \cdot y_2 \oplus \dots \oplus x_n \cdot y_n} \left| {y_1 y_2 \ldots y_n} \right\rangle =$

（コンパクト化のために再割り当て）

$=\frac{1}{\sqrt{2^n}} \sum \limits_{y \in \lbrace 0,1 \rbrace^n} (-1)^{(x, y)} \left| y \right\rangle,$

どこで $\oplus$ -2を法とする加算、および2を法と $(x, y)$ するスカラー積。

最初の時点で、システムは状態に $\left| {q_0} \right\rangle \left| {q_1} \right\rangle = \left| 0 \right\rangle^{\otimes n} \left| 1 \right\rangle$ あり、アダマール変換の影響下で状態になります。

$H^{\otimes n} \left| 0 \right\rangle^{\otimes n} (H \left| 1 \right\rangle) = \frac{1}{\sqrt{2^{n+1}}}\displaystyle\sum_{x=0}^{2^n} \left| x \right\rangle \big(\left| 0 \right\rangle - \left|1 \right\rangle \big).$

オラクル $U_f$ システムを状態にします

$\frac{1}{\sqrt{2^{n+1}}}\displaystyle\sum_{x=0}^{2^n} \left| x \right\rangle \Big(\left| {f(x)} \right\rangle \oplus \big(\left| 0 \right\rangle - \ \left| 1 \right\rangle \big) \Big) = \frac{1}{\sqrt{2^{n+1}}}\displaystyle\sum_{x=0}^{2^n} \left| x \right\rangle \Big( \left| {f(x)} \right\rangle - \left| {f(x) \oplus 1} \right\rangle \Big).$

固定引数の場合 $x$ 機能 $f(x)$ 値0をとると、前の係数 $\left| x \right\rangle$ は変化しません。そうでなければ、符号が変化します。この観察に基づいて、現在の状態を次のように書き換えることができます。

$\frac{1}{\sqrt{2^{n+1}}}\displaystyle\sum_{x=0}^{2^n} (-1)^{f(x)} \left| x \right\rangle \big( \left| 0 \right\rangle - \left| 1 \right\rangle \big).$

この段階で、未使用の最後のキュービットを破棄し、最初の $n$ キュービットにアダマール変換を適用して状態を取得します

$H^{\otimes n} \Big( \frac{1}{\sqrt{2^n}}\displaystyle\sum_{x=0}^{2^n} (-1)^{f(x)} \left| x \right\rangle \Big) = \frac{1}{2^n}\displaystyle\sum_{y=0}^{2^n} \Big( \displaystyle\sum_{x=0}^{2^n} (-1)^{f(x) + x \cdot y} \Big) \left| y \right\rangle.$

そして $x \cdot 0^n = 0$ 、結果を観察する確率 $\left| {0^n} \right\rangle$ は

$\frac{1}{2^n}\displaystyle\sum_{x=0}^{2^n} (-1)^{f(x)} = \begin{cases} 1 &\text{, $f(x)$ }\\ 0 &\text{, $f(x)$ } \end{cases}.$

以上です。量子コンピューティングのかなり単純化されたモデルを調べ、古典的なコンピューターでエミュレートするためのPythonミニフレームワークを作成し、最も単純な「実際の」量子アルゴリズムの1つであるDeutsch-Jojiアルゴリズムを分析しました。怠け者ではない人のための猫です。記事を読んでトピックを理解しました。

→コードはGitHubで入手できます

読んでくれてありがとう！たとえば、プロファイルを購読し、コメントを残し、有用なことを行います。追加は大歓迎です。

文学

[1] M. Vyalyi、「量子アルゴリズム：可能性と

制限」
[2] A. S.ホレボ、「情報の量子理論の紹介」
[3] MAニールセン、量子情報理論

PS：habrのフォーミュラ-吸います。おかげで、ローマParpalakサービスupmath.meは、非常に多くの数式を持つポストなしには不可能だったでしょう。

2つの機能があります。