Duplo Railroad Tycoon：最大カバレッジの鉄道ネットワークの合成

サンタクロースは子供たちにデュプロ鉄道をもたらしました。 レールセグメントは非常に簡単に相互接続されており、いくつかの小さな閉鎖経路を構築し、駅を設置して、列車が輪になって走っているのを見ることができます。 時々彼は停止し、子供はコラムからエンジンを「一杯にする」必要があります。その後、エンジンは再び作動します。



最も簡単な方法の例を次に示します。







この列車は3周目を過ぎてすぐに退屈してしまい、Thingiverseを掘り下げて10万回目に役立つ3Dプリンターの使用を試みました。 そして突然、Duploエンジン専用の矢印セグメントが見つかりました 。



矢印は次のように機能します。3つの入力と出力があります。最初、2番目、3番目に呼び出しましょう。 列車が最初または2番目のノードに入ると、矢印は常に3番目を通過します。 この場合、矢印は対応するノードに切り替わります（つまり、最初のノードから入った場合、最初のノード、2番目のノードから入った場合、2番目のノードに切り替わります）。 しかし、彼が3番目のノードに入ると、出口は矢印の状態に依存し、最初のノードと2番目のノードの両方を出ることができます。 すなわち：



'1'-> '3'（矢印は '1'に変換されます）

'2'-> '3'（矢印は '2'に変換されます）

「3」->矢印が「1」にある場合は「1」、それ以外の場合は「2」



そのような矢印をいくつか印刷し、「普通の」鉄道を集め始めました。 なんとなく悲しいことにすべてが判明しました-蒸気エンジンは途中までしか移動せず、いくつかのリングに張り付いていて、離れたくありませんでした。



問題1（単純）：すべてのノードが相互接続されるように、ネットワークにはいくつの矢印セグメントが必要ですか？ 道路は、行き止まりのない連続したものでなければなりません。





しかし、一生懸命働いて、最も簡単なオプションとして、数日で問題を解決しました。 訪問するために来た友人は、緊張せずに5分でそれを決定しました:)



各矢印を文字で示します。ノードは上記の例と同じです。 つまり 私たちのネットワークにはノード['a1'、 'a2'、 'a3'、 'b1'、 'b2'、 'b3']があります。





しかし、さらに矢印をとるとどうなりますか？ うーん、単純な解決策について考えすぎたら、もうそれをマスターすることはないでしょう。 しかし、コンピューターはマスターします！ しかし、どうすればこのタスクに到達できますか？ 私は数日間苦労しましたが、これに何らかの検索を追加しようとして、すべてがほぼすべてのものを捨てようとしましたが、突然アイデアが紙に解決策を書くようになりました。



トラック全体をステップに分割しました。



現在の状態→矢印の遷移→接続セグメントに沿った遷移→矢印の新しい状態を記憶する



つまり 上記のソリューションの場合、遷移は次のようになります（デフォルトの矢印状態：a3-> a1; b3-> b1）：



a1-> a3-> b3（a3-> a1; b3-> b1）

b3-> b1-> b2（a3-> a1; b3-> b1）

b2-> b3-> a3（a3-> a1; b3-> b2）##矢印b3が切り替わっていることに注意してください



残りは簡単です：

• 指定された数の矢印に対して可能な道路構成をすべて生成します
• 各道路で：
  
  
  • 電車を10回運転し、各ノードの移動回数をカウントします
  • 通路が0または1のノードがある場合、これはモードに入るとシステムが無限ループに陥ったことを意味します
  • そのようなノードがない場合、列車は道路全体に安全に急行します。これが必要なことです！

とてもシンプルなので、2日間テーブルに頭を突っ込んで、最終的にスタックオーバーフローに関するアドバイスを求めました。そこで、数分で銀の大皿にいくつかの解決策が与えられました。



トラックジェネレーター（タスクを宣言してネタバレに入れることはしません-私のような人にとっては、これは非常に残酷な冗談かもしれませんが、興味のために自分で解決しようとします）：

def getTrack(l): # recursion anchor, basic case: # when we have 2 nodes only one pair is possible if len(l) == 2: yield [tuple(l)] else: # Pair the first node with all the others for i in range(1, len(l)): # Current pair pair1 = [(l[0], l[i])] # Combine it with all pairs among the remaining nodes remaining = l[1:i] + l[i+1:] for otherPairs in getTrack2(remaining, 1): yield pair1 + otherPairs
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

トラックラティス：

 def solveTrack(track): #        nodeCount = {} for n in nodes: nodeCount[n] = 0 railTr = None jointTr = 'a1' while True: pos = jointTr #  nodeCount[pos] += 1 #  railTr = getTransition(track, pos) #    (    ) nodeCount[railTr] += 1 #    jointTr = tj[railTr] #   (    ,        ) if railTr[1] in ['1','2']: ##  tj[railTr[0]+'3'] = railTr if max(nodeCount.values()) > nodesTrace and min(nodeCount.values()) < 3: #       nodesTrace ,     .   -   -     . #print "Infinite cycle detected" break #sol = "{}\t{}\t{}\t{}\t{}".format(pos, railTr, jointTr, tj['a3'], tj['b3']) #print sol if max(nodeCount.values()) > nodesTrace * 1.5: print "-------------------------------------------------------\n" print "Simulation complete!" print '\nNodes: ', nodeCount, "\n" print "Solution: ", track break return
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

入力データのノードのリスト、矢印のノード間の遷移を設定し、ソリューションの検索を開始するだけです！ やった！

 tj = {} #  nodes = [] #  ##create joints transition table for jt in range(nJoints): tj[idxs[jt]+'1'] = idxs[jt]+'3' tj[idxs[jt]+'2'] = idxs[jt]+'3' tj[idxs[jt]+'3'] = idxs[jt]+'1' nodes.extend((idxs[jt]+'1', idxs[jt]+'2', idxs[jt]+'3'))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

うーん、しかし、4本矢印の道に解決策はありません。 そして、6（私は数時間待っていました）-どちらでもありません。 以上です。 夢の終わり。



でも。 しかし、矢印の一部のみを切り替え可能にし、残りを凍結するとどうなりますか？ たとえば、次のように：

 if railTr[0] in idxs[:nSwitchableJoints]: ## nSwitchableJoints -     if railTr[1] in ['1','2']: ##  tj[railTr[0]+'3'] = railTr
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして出来上がり-多くの解決策があります！ 私はもっ​​ときれいなものを選択しようとしました:)









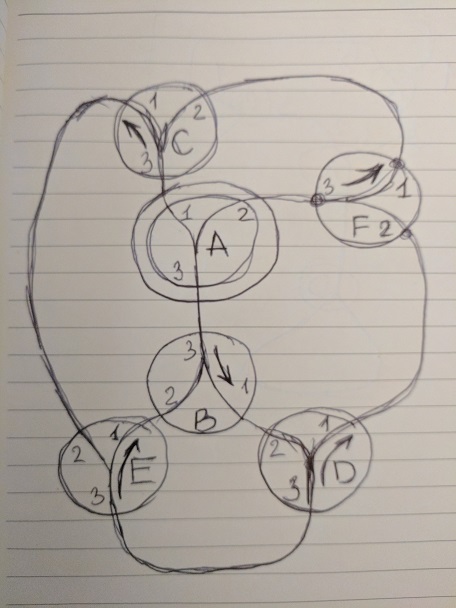
ここでは、矢印「a」のみが切り替え可能で、残りの3つは常に1つに切り替えられます。

このトラックはソリューションに対応しています。

 [('a1', 'c3'), ('a2', 'f3'), ('a3', 'b3'), ('b1', 'd2'), ('b2', 'e1'), ('c1', 'e2'), ('c2', 'f1'), ('d1', 'f2'), ('d3', 'e3')] nSwitchableJoints = 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

今のところすべてです！