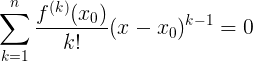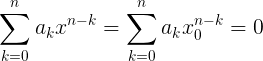親愛なるKhabrovites、私は歓迎します! 数学に近い記事のサイクルを継続します 。前の記事はこちらにあります 。 私は数学のアマチュアであり、その道徳的および美的側面を扱っているだけであり、私のアイデアはあなたにとって面白くない/役に立たないように見えるかもしれないことを思い出させてください。 だから:
まず第一に、正しいコンテキストは、この文脈で「等価性」という用語の説明に公理を導入することです。
- 横軸の座標がある場合
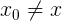 数値セットから、次の条件を満たす。
数値セットから、次の条件を満たす。
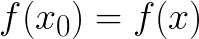
それは信じられています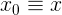 (つまり
(つまり  と同等
と同等 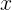 )
)
この記事のフレームワーク内でのこのような公理は便宜上のものであり、厳密に言えば、完全に正しいわけではありません。
そしてすぐに、「ごめんなさい、なぜこれが必要なのか」という伝統的な質問に答えるのは良いことです。 私は答えます-少なくとも、多項式方程式の残りの根(方程式から関数への移動)を検索し、1つの根しか知りません。 さまざまなあまり明らかでないこと。 次に、この問題の解決方法を説明し、一般的な形式でアルゴリズムを示します。 恵みに興味がある人のために、猫をお願いします。
次のクラスの関数で作業することに注意してください。
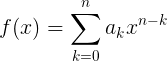
sigmaが何であるかわからない場合は 、これが次と同等であることを明確にする必要があります。
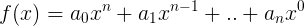
これは、多項式である関数の一般的な形に他なりません。 最後に、具体的な例を使用して理解可能なタスクを定式化して、何が起こっているのかをよりよく理解しましょう。 したがって、3次の多項式、つまり3次の方程式があります。
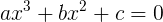
タスク:方程式の根の1つ(任意の数値セットから- 有理であっても、 複雑であるなど)を知って、方程式の残りの根を見つけます。 はい、見つけるだけでなく、 より低い次数の方程式を解くことによって!
それでは、方程式から関数に移りましょう。
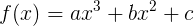
そして、楽しみのために、すべての非ゼロ派生関数を見つけます。
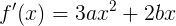
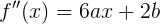
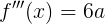
さて、見つかったので、関数をテイラー級数 ( ここで、
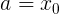 ):
):
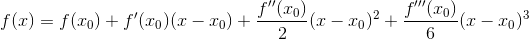
さらに、上記の等価性の公理を思い出します
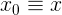 私たちのコンテキスト:
私たちのコンテキスト:
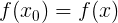 [平等のおかげで、
[平等のおかげで、 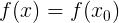 ]
]
何にも似ていませんか? そう! これは、関数のテイラー級数展開の最初の項です。 そして、明らかに、平等が同一であるためには、展開の残りの項が消えなければなりません。 言い換えれば:
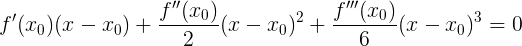
次の明白なルールを使用します。
- 少なくとも1つ以上の因子がゼロに等しい場合にのみ、積はゼロになります。
そして、私たちはただ乗算することができます
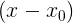 大括弧から外します:
大括弧から外します:
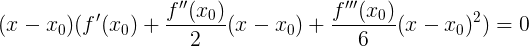
次に:
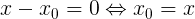
適していない 、なぜなら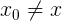 、種のトートロジーがあるからです
、種のトートロジーがあるからです 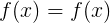
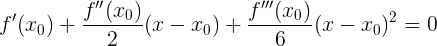
これは、作業を完全にゼロにする2番目のケースです。 すぐに誘導体を置き換えましょう:
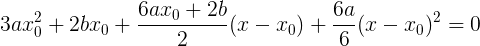
少しカットしましょう。
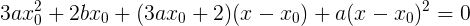
そして見よ! 方程式は2次(2次)であることが判明しましたが、元の方程式は3次( 3次)でした。
に関する決定
 次のルートを取得します。
次のルートを取得します。
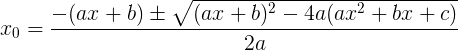
明らかに、私たちの機能についてはこれから次のようになります。
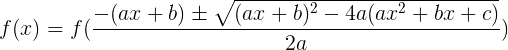
これは、方程式に何を与えますか? そして、方程式の根の1つを知っているという事実は、他の2つを見つけることができます(そして2次の複雑さのために)。
帰結 :度の方程式の根の1つを知っている
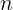 、方程式の次数を下げることができます
、方程式の次数を下げることができます 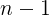 、およびルートは、任意の標準の番号セットから取得できます。
、およびルートは、任意の標準の番号セットから取得できます。
より具体的な例を見てみましょう:
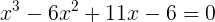
求められた方程式の根からは
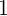 。 また、方程式を(上記のアルゴリズムに従って)3次関数として表すと、次のようになります。
。 また、方程式を(上記のアルゴリズムに従って)3次関数として表すと、次のようになります。
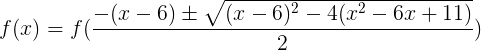
グラフは次のとおりです。

それから私たちのルートのために
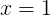 :
:
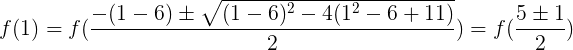
それは:
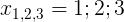
したがって、2次方程式を解くことにより、3次方程式の他の2つの根を見つけました。 よく知られた円には、コーナーを分割する方法があり、次数を下げることもできます。 ただし、整数係数でのみ機能します(つまり、有理係数は整数に変換する必要がありますが、複雑な係数はまったく使用できません)。
同様の「等価」式がn次多項式の(非)単調性の条件を意味することも興味深い。 次のように作成できます。
多項式で検出された場合過激でも
(どこ
-過激な表現)次のプロパティを形成できます:
もしあれば不等式が成り立つ
、その後、目的の関数のグラフはセット全体で単調です
。 逆の場合も当てはまります
。
なぜそう はい、それが満たされない場合、我々は単に計算できないためです
 DLDルート式のため。
DLDルート式のため。
おそらく、多項式関数の横軸の同等の点を見つけるための一般的なアルゴリズムを定式化する時が来たのでしょう。
一般形式の任意の次数の多項式形式の方程式があります。
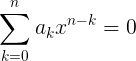
方程式から関数に渡します:
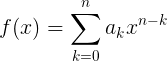
関数をテイラー級数で展開します。:
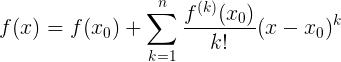
私たちは見つける必要がありますしたがって:
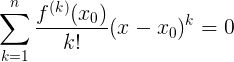
次に:
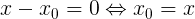
ふさわしくない、種のトートロジーがあるからです
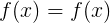
方程式を解く( 次数は最初のものよりも小さい )、その根は等価である
。
現在、特に、次のことが当てはまります。
同等のポイントが見つかりました 。
また、(非)単調性の条件と、目的のアルゴリズムからのさまざまな結果についても忘れないでください。 また、通常、単調性条件は、方程式の根の根のODZによって決定されることも注目に値します
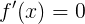 。 このようにして、「他のルート」だけでなく、他のルートも検索できることを思い出してください。
。 このようにして、「他のルート」だけでなく、他のルートも検索できることを思い出してください。  そのような:
そのような:
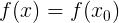
また、Abel-Ruffiniの定理によれば、アルゴリズムは次数5を含む一般形式の多項式までしか機能しません(4次より大きい高次方程式の根は有理関数(根、など)として表現できないため) )
日曜日のタスクを完了しました。これは私が逸脱するためです。
ご清聴ありがとうございました!