
私のドキュメントスキャンプロジェクトの不要な製品は、大量のステープルが削除されたことです。
先日、私が発見したのは、廃棄されたブラケットの1つをつかんで持ち上げると、絡み合ったねじれた金属のボール全体が上昇し、ボウルの底に数個のブラケットのみが残ることです。 これに気づいたとき、私は最初に「うーん、これは面白い」と考えました。 それから「ああ、もちろん:Erdős-Rényi。」 そして、3番目の考え...まあ、私はまだそれに取り組んでおり、4番目、5番目、6番目にも取り組んでいます。

ErdősとRényiは、PaulErdősとAlfrédRényiであり、50年前に「Evolution of Random Graphs」に関する著書を執筆しました(ハンガリー科学アカデミー数学研究所の出版物、1960、5:17–61)。 彼らの記事は、数学文献におけるランダムグラフの完全なデビューではありませんでしたが、理論の元々の起源と考えられています。
Erdős-Rényiプロセスの1つのバージョンでは、多くの孤立した頂点nから始めて、ランダムなエッジを1つずつ追加します。 特に、各段階で、接続されていないすべてのペアの中から任意の2つの頂点を選択し、それらの間にエッジを描画します。
面の数がn / 2に達すると、グラフの性質に劇的な変化が生じることがわかります。 このしきい値を下回ると、グラフは多くの小さな孤立したコンポーネントで構成されます。 n / 2を超えると、フラグメントは1つの巨大なコンポーネントにマージされ、ほぼすべての頂点が含まれます。
「巨大成分の誕生」については、後でさらに詳細な記事で詳細に説明しました-ランダム構造とアルゴリズム(1993、4:233-358)のすべての問題をカバーし、Svante Janson、Donald Knut、Tomasz Lutzaka、Boris Pittelによって書かれました。
Erd-s-Rényi伯爵とステープルのボールとの関係について私に考えさせたのはなぜですか? 私の考えでは、長く真っ直ぐなものがあり、ブラケットの中央部分はグラフの端に対応し、互いに噛み合うことができる曲線部分は頂点です。 したがって、1つのブラケットは、1つのエッジに沿って接続された2つの頂点で構成されるグラフです。 2つのブラケットが接続されると、2つの頂点がマージされ、接続された3つの頂点と2つのエッジのグラフが残ります。 各ブラケットはグラフの1つのエッジと最大2つの頂点を与えるため、エッジの数は少なくとも頂点の数の半分に等しくなければなりません。 したがって、ErdsとRényiによれば、巨大なコンポーネントが形成されると、グラフは常にしきい値を超えます。
この分析の計算部分についてはすべて明らかなように思えますが、残りの部分はそれほど簡単に理解できないと思います。 ブラケットボールで何が起こるかに関係なく、システムの進化は、固定された頂点のセットに顔を追加するErdős-Rényiプロセスによってあまりうまくモデル化されていません。 代わりに、各ブラケットは2つの面と2つの頂点を提供します。
ブラケットの梁を互いにくっつける分岐点は、ブラケットが一緒に保持されているときの頂点のマージです。 Erdős-Rényiプロセスにはそのような合併はありません。 ここでの主な問題は、Erd-s-Rényiグラフが純粋にトポロジカルであることです。距離の概念はなく、任意の2つの頂点がそれらを接続するエッジを持つことができます。 ただし、ブラケットグラフには重要な幾何学的制約があります。 2つの頂点をエッジで接続できるのは、頂点間の距離がブラケットの長さにほぼ等しい場合のみです。
幾何学的構造には、おそらく液体と固体の分子構造を説明するさまざまな種類のモデルを構築する試みが含まれます。 たとえば、水分子は水素結合のネットワークによって互いに接続されています。 1つの分子内の各水素原子は、別の分子の酸素原子と結合することができます。 ただし、通信を任意の距離まで延長することはできません。 それらは隣接する分子間でのみ広がります。 その結果、3次元構造が得られました。その主な動機は、中心に酸素原子があり、四隅に水素原子がある四面体です。 (氷域として知られる2次元モデルの概略図もあります)。 ステープルでこのようなことがどのように起こるか想像できます。2つの曲がった端が他の近くのステープルとの結合として水素結合を形成します。
しかし、そのような化学元素には問題があります。 原子は固定された原子価を持っています(多かれ少なかれ-言い争わないようにしましょう)。 たとえば、水中では、各水素原子は1つの酸素原子のみと水素結合を形成できます。 しかし、ステープルのフック端が他のブラケットの片方の端だけにくっつくことができると信じる理由はありません。 実際、このような制限が発生した場合、ブラケットは、密集したクラスターではなく、チェーンとリングのみを形成できます。 ステープルクラスターをよく見ると、同じポイントで3つ以上のステープルがロックされている場所を簡単に見つけることができます。 ステープルの蓄積を注意深く見て、少なくとも6つのステープルがくっついているステープルを見つけました。
モデルがメイングラフに提供できる別の物理プロセスは、限られた分布の集約です。 これがフィリグリーパターンの原因となるメカニズムです。
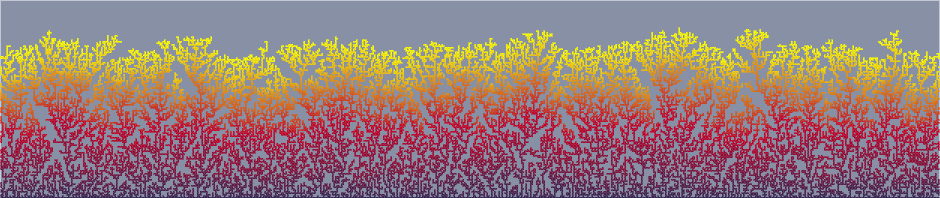
これは、ベースに衝突するか、すでにベースに直接または間接的に接触している別の粒子に触れるまでランダムにドリフトする粘着性粒子によって行われます。
ここで考慮すべきもう1つの要因は、空間次元が間違いなく重要であることです。 一方では、これは単に3次元で操縦する機会を増やし、隣人にしがみつく機会を増やします。 しかし、特にブラケットの場合には、別の理由があります:平面にチェーンされているため、それらを接続することは困難です。

平らな板の上に散らばって、激しく回転していても折り畳むことを拒否します。 その理由は、明らかに、ブラケットが90度回転して係合できる場合にのみ安全なジョイントが形成されるからです。 この点で、結束プロセス中にフックの端が約180度曲がり、基本的に紙から引き出された後90度以上の角度を維持する、非常に多様な形状のステープルを使用することが重要と思われます。
光沢のある新しいブレースがどのように振る舞うのか疑問に思って、実験を行いました(材料と方法:630スタンリーボスチッチチゼルポイントステープル、モデルSBS191 / 4CP、オープンジョースウィングラインステープラーから新たに分配)
控えめに言っても、その結果に驚きました。 ステープルの蓄積はややゆるやかで細かくなりましたが、その要点はそれほど大きく異なりませんでした。 繰り返しますが、私たちは巨大なコンポーネントの誕生を目の当たりにしています。
コメント
Barry Cipra :新しいステープルで実験を繰り返し、ステープルを追加するたびに一時停止し(10ステープルまたは20ステープルごとなど)、ボウルに既にあるものを振ってから、大きな混雑がどのように形成されるかを見る価値があるかもしれませんブラケットの1つを取ります。 おそらく、ブラケットを数回追加する間のシェイクアップとポーズを数回繰り返して、統計を観察するとよいでしょう。 ステープルのボールで上昇するステープルの(平均)割合は、ボウル内のステープルの合計数が約100になるまで非常に小さくなり、その後100%近くまで増加し始めると想定しています。 これから論理曲線は続きますか? もしそうなら、どれ? いずれにせよ、これは素晴らしい観察です!
ヨンコウ :とても美しい仕事です。 ボウルの形が役割を果たしているのだろうか。
私は平板実験を本当に理解しています...しかし、前のものの上にブレースを追加しましたか?(ボウルでこれを行うと圧力がかかります)? また、より限られた容器、例えば、in vitroでそれらを追加した場合に何が起こるかも興味深いです。
Unekdoud :ステープルなど、さまざまなオフィス機器でこれを行うことを検討すべきだと思います。 また、ホッチキスのサイズが役割を果たしていますか?
さまざまな形を組み合わせて「合金」を形成します。 それらを氷中の不純物と考えると、構造に特定の重要な影響が生じる可能性があります。 氷の凍結温度の類似物はありますか? 密度の変化は何ですか?
必然的に、ボウルのサイズが重要になります。 おそらく、非凸形状の巨大なコンポーネントを作成する可能性があります。 構造自体に関しては、サブグラフとループのプロパティ、および頂点密度などを調べるために、グラフの形で実際に表示することを検討する必要があります。 少量の接着剤を追加して、構造を保持し、観察しやすくすることができます。 磁石や磁化はさみを使用して構造を攪拌するなど、別の方法を使用して巨大なコンポーネントを作成すると、グラフのプロパティは変わりますか? ブレースがオイルに浸漬された場合、これはどのように変化しますか? プロセスの途中で加熱または冷却された場合はどうなりますか? 異なる周波数の振動はどうですか? コンポーネントのサイズに関しては、ステープルを追加し続けて、どれだけ大きくなるかを確認することができます。 2つのコンポーネントを組み合わせることは可能ですか? そして、これは物理学と化学以外にどこに適用できますか? ソーシャルネットワークのコンテキストでこの実験を再現することも可能です。 同様の効果は、異なるスケールで、またはおそらく完全に異なる場合に観察されます。
ブライアン :バリーとヨンコウとウネクドウドにいくつかの興味深い質問を提起し、研究のさらなる方向性を提案してくれてありがとう。 他のことを言う前に、これは、誰でもプレイできる実験科学のまれなケースの1つであることに注意したいと思います。 材料はすぐに入手できます。 調査に資金を提供するためにNSFの助成金は必要ありません(ただし、オフィス用品店に資金を求めることができると思います) どんな犠牲を払っても:ホッチキスをつかんで参加してください。 科学的協力と真実の熱心な追求の精神で、私は使用済みのステープルの在庫を共有する準備ができています。 バリーは、ステープルの小さなセットのクラスターの外観について尋ねます。 私はこれがどのように起こるかわかりません。 Erdős-Rényiグラフでは、既知の結果は無限のN内でのみ厳密に有効ですが、実際にはグラフ理論では無限大は非常にまれです。
Unekdoudは、到達可能な最大の輻輳について尋ねます。 繰り返しますが、私は知りませんが、もちろん、物理的な制限がなければなりません。 ある時点で、クラスターの重量は、すべてが保持するブラケットの強度を超えます。
ボウルの形状、攪拌スタイル、ステープルのサイズなどに関する未解決の質問については、これらの要因が重要であるという事実に加えて、明確な分析につながるシステムはありません。 この厄介な金属ステープルの世界から抜け出し、計算のシミュレーションと数学的な解決が可能なモデリングの分野に入りたいと思います。
しかし、もちろん、私はそのようなモデルを持っていません。
最後にペーパークリップについて。 これは、アメリカの科学者同僚ヘンリーペトロスキーの領土です。 彼はそれについて本を書いて、それを彼の分野のままにしておきました。
Kevembuangga :この種の「研究」は非常にばかげていると思いますが、高性能プロセッサの開発の成功のためにビデオゲームに夢中になっている人々に感謝するように、一部の人々がそれを行うことを心から感謝しています。
ベン :ランダムグラフについて話し始めたときに最初に考えたのは、ブラケットの「平らな」部分が上部になり、「端」が端になります-最後に、すべての端があなたが説明した「接続」を形成することです議論された水分子。 ステープルがボウルに置かれたり、ボウルの周りに混ぜられたりすると、エッジ間の結合がランダムに形成されます。 次に、表面からボウルに2次元から3次元に変更すると、任意の2つの頂点間でランダムな結合が形成される可能性が変わります。 表面上は予想される結合の数がn / 2未満であるのに対し、ボウルではそれがどれほど大きいかを考える必要があります。
Jess :私のアイデアは、ホッチキスは全体であるということです。2つのブラケットが互いに引っ掛かると上部と端が形成されます。 これは、提案されている合併プロセスよりも簡単に思えます。 エッジの概念は、粗雑な物理的類似物よりも2つのオブジェクト間の接続にあるとは考えていませんか?
Stephan Mertens氏:一種のエントロピーラチェットメカニズム(少なくとも一部)が巨大なコンポーネントの形成に関与していることをお勧めします:2つのブラケットがかみ合うことができる多くの方法がありますが、これには調整された動きが必要ですステープル。 そして、常に大きな結び目を形成する引き出しの電源コードにも同じ議論が当てはまると思います。
その他の資料:
- ジャイアントコンポーネント
- ジャイアントコンポーネントの誕生(Knuth)
- 接続G(n、p)、ジャイアントコンポーネント、特性番号G(n、p)
- 講義9-ランダムグラフでの巨大コンポーネントの出現に関する定理
- システム生物学-M.ゲルファントネットワークス、BBC 4年目の「比較ゲノミクス」。 -プレゼンテーション
- サイクルからジャイアントコンポーネントまで、社会的ガイド付きツアー
- NetLogoモデルライブラリ:サンプルモデル/ネットワーク
出版サポート-Edisonは 、 プロバイダー向けの課金システムを 開発し、インターネットを介した税申告用ソフトウェアも開発しています 。