テンソル分解とその応用。 Yandexでの講義

Data Festでの以前の講義は、新しい種類の検索を構築するために必要なアルゴリズムに専念しました 。 今日のレポートも、ある意味で、異なるアルゴリズムに関するものであり、むしろそれらの多くの基礎となる数学に関するものです。 科学博士であり、Skoltechの計算手法グループの責任者であるIvan Oseledetsは、行列分解について聴衆に語りました。





カットの下-デコードとほとんどのスライド。

---

線形代数を扱う小さな-比較的機械学習-のコミュニティがあります。 線形代数があり、その中に多重線形代数、テンソル分解を扱う人々がいます。 私は彼らに関係しています。 そこではかなり多くの興味深い結果が得られましたが、コミュニティが自分自身を組織化して外に出ることはできないため、これらの結果の一部は不明です。 ところで、これは線形代数にも当てはまります。 NIPS、ICMLなどの主要な会議の記事を見ると、線形代数の些細な事実に関連する多くの記事を見ることができます。 これは起こりますが、それでも起こります。



テンソル展開について説明しますが、最初にマトリックス展開について説明する必要があります。







行列。 ただの2次元テーブル。 行列分解は、ブール素数の積の形式での行列の表現です。 実際、それらはどこでも使用され、誰もが携帯電話を持ち、座っている間、線形システムを解決し、データを送信し、行列を分解します。 確かに、これらのマトリックスは非常に小さく、4x4、8x8です。 しかし、実際にはこれらの行列は非常に重要です。



LU分解、ガウス分解、QR分解があると言わざるを得ませんが、主に特異分解についてお話します。これは、何らかの理由で、たとえば、私たちの大学の線形代数コースでは、忘れられがちです。 彼らは、ジョーダン形式のような計算科学の観点からそのようなナンセンスを読みます。そして、それはどこでも使われません。 特異分解は通常、最終的にどこかにあり、オプションなどです。これは間違っています。 Golubとvan Lounの 「Matrix Calculations」という本を取り上げると、LU-とQR-のどちらでもなく、特異分解で始まります。 積の形式のマトリックスのこの表現は、ユニタリ、対角、ユニタリです。



マトリックス分解について、良いことは、それらについて多くが本当に知られていることです。 基本的な分解には、効果的なアルゴリズムがあり、安定しています。MATLABで呼び出すことができるソフトウェアがあります。Pythonでは、Fortranで記述されています。 これをカウント可能な単一の操作と正しく見なすと、正確な結果が得られることが確実になります。勾配降下を行う必要はありません。 実際、これは操作の1つのクォンタムです。 問題をマトリックス展開の計算に減らした場合、実際にそれを解決しました。 これは、たとえば、さまざまなスペクトル法の基礎となります。 たとえば、EMアルゴリズムがある場合、反復アルゴリズムであり、収束が遅くなります。 そして、スペクトルメソッドを取得できた場合、あなたは素晴らしく、ワンステップのソリューションが得られます。



直接同じ特異分解は問題を解決しませんが、一般的な問題を解決するための一種のビルディングブロックです。 携帯電話に戻ります。 この例は、明らかな理由で私を悩ませます。私たちは本当にそれを必要とする通信会社と協力しています。







特異分解とは何かを見て、それをインデックス形式で書くと、次の式が得られます。 これは古典的な古いアイデアにつながります-大学の最初のコースに戻ると、変数の分離につながります。 xをtから分解し、ここでIをjから分離し、1つの離散インデックスを別のインデックスから分離します。つまり、1つの変数からの関数の積の形で2つの変数から関数を表します。 この形式の関数がほとんどないことは明らかですが、そのような関数の合計を書くと、かなり広いクラスになります。



実際、特異分解の主な用途は、このような低ランクの近似の構築です。 これはランクrの行列であり、当然、ランクが行列の合計サイズよりも大幅に小さい場合に関心があります。



ここですべてが順調です。 ランクを修正し、最適な近似値を見つけるタスクを設定すると、特異分解の解が与えられます。 実際、はるかに多くのことが知られており、特異分解の助けを借りた場合よりも速く行うことができます。行列のすべての要素を計算することなく、などです。大きな美しい理論があります-低ランク行列の理論は、発展し続けており、まだ閉じられていません。







ただし、閉じられていませんが、3つ以上のインデックスを作成します。



このトピックに対する私の最初の関心は純粋に理論的なものでした。 一部のアプリケーションでは、マトリックスを使用して何かを実行し、分解し、表現することができます。これまでのところ、どのアプリケーションでも問題ありません。 最後に言います。



そして、A（i、j）の代わりにA（i、jk）を記述し、変数を分離しようとするとどうなりますか。 したがって、テンソル展開の問題は完全に自然な方法で発生します。 テンソルがあります-テンソルとは、多次元配列、単純な2次元テーブルを意味します-これらの多次元配列を圧縮して、大まかに言って、低パラメーター表現を構築し、通常は美しい言葉で言うと、次元の呪いを克服したいと思います。 実際、この用語-それは、いつものように、1961年のベルマンの作品で、まったく異なるタスクとまったく異なる関係で登場しました。 しかし、現在、dのnは非常に悪いという意味で使用されています。 dを増やしたい場合、指数関数的な成長などがあります。



最も一般的な意味での因数分解：アプリケーションで発生する特定のクラスのテンソルを選択し、そこからテンソルをすばやく回復できるような低パラメーター表現を構築しようとしています。 また、パラメーターはほとんどありません。 原則として、ニューラルネットワークは、ある意味でテンソルを近似する問題を解決するということができます。なぜなら、それらは、どこか別のパラメータ空間からマッピングを構築しようとしているからです。







因数分解の問題、つまり単純なオブジェクトの積の形式での表現に、テンソルを持つ行列と行列の積がある場合、テンソルの決定はより複雑なタスクです。 しかし、低ランク近似の不完全な特異分解のインデックスレコードを見ると、当然、同様の式が得られます。 彼女がいる。 1つの離散変数の関数の積であるオブジェクトでテンソルを近似し、関数t1に関数t2を掛けようとしています。 アイデアは完全に自然です。 用語が1つしかない場合は、何も近づけません。 そして、あなたがかなり少数のパラメーターを取ることを許可する場合、テンソルの非常に興味深いクラスが発生します。これは、メソッドの多くの問題で明示的または暗黙的に使用されます。 ほぼこの形式は、量子化学で波動関数を表すために使用されていると言えます。 反対称性もあり、製品の代わりに決定要因が現れます-しかし、科学の巨大な分野全体は、実際、そのような分離可能な近似に基づいています。



したがって、もちろん、プロパティを調べたり、ここで何が起こっているかを理解したりすることは興味深いことです。







このエンティティ-1つの変数の関数の積の合計としての表現-は標準分解と呼ばれます。 最初に提案されたのは1927年です。 それから、数学から遠く離れて使用されました。 統計学、ケモメトリックス、Psychomatrixなどの雑誌で、人々がデータキューブを受け取った作品がありました。 兆候があります-何かが起こりました。 したがって、彼らは多要素モデルを構築しました。 これらの要因のマトリックスは、いくつかの要因として解釈できます。 これらのうち、いくつかの結論を導き出すことができます。



パラメーターの数を数えると、dnrパラメーターが取得されます。 rが小さい場合、すべてが正常です。 しかし、私が解決しようとしている問題は、原則として、たとえそのような近似が存在することがわかっていても、それを計算することは困難な作業であることです。 ランクを計算するタスクのように、一般的な場合はNP複雑であると言うことさえできます。 マトリックスの場合、これはそうではありません。 行列のランクを計算できます-たとえば、ガウス例外を使用すると、これは多項式の演算数で実行できます。 ここではすべてが間違っています。



サイズが9x9x9のテンソルの例がありますが、その最小項数の正確な値はまだ不明です。 それは23以下、21以上であることが知られています。スーパーコンピューター、単純な多項式：これは、多項方程式系の可解性の問題です。 しかし、そのようなタスクは非常に難しい場合があります。 そして、テンソルは実際的に重要です。 このテンソルのランクは、行列乗算アルゴリズムの複雑度インデックスに関連しています。 Strassenの対数は7からのバイナリです。 したがって、実際には、指数を計算するタスクは、一部のテンソルの標準ランクを計算することになります。



多くのアプリケーションでは、特定のテンソルのこの表現はうまく機能します。 しかし、一般的に、このタスクは悪いです。



最近、非常に尊敬されている人々の仕事が現れました。そこで彼らはこの考えをディープニューラルネットワークで分離変数と結び付け、いくつかの結果を証明しようとしています。 実際、それらを解読すると、それらはテンソル分解に関する非常に興味深い代数的結果です。 結果をテンソル展開の言語に翻訳すると、標準的なテンソル展開が別のテンソル展開よりも優れていることがわかります。 どちらが良いかはまだ示していませんが、標準的なものです。 この意味でCanonicalは悪いです。 この結論は、標準的なアーキテクチャが浅く、浅いが、深く、より広範でなければならないなどの事実によって正当化されます。



したがって、これにスムーズに移行してみましょう。 正規分解の場合、最適化アルゴリズムはゆっくり収束します。つまり、沼地などがあります。この式を見ると、線形代数に精通しているすべての人が、使用できるアルゴリズムをすぐに理解できます。 勾配降下法を使用できます-1つを除くすべての因子を修正し、線形最小二乗問題を取得します。 しかし、この方法は非常に遅くなります。



このようなモデルには1つの優れた特性があります。それでも解決策が見つかった場合、それは些細なことまで唯一のものです。 たとえば、s、s-1を挿入できる場合、行列分解の問題はありません。 正規分解が計算される場合、それが唯一のものであり、それは良いことです。 しかし、残念ながら、計算が難しい場合があります。







Tuckerの別の分解があります。 それはある種の心理測定でした。 アイデアはここにある種の接着要素を導入することです-そのため、それぞれの要素の間にはつながりがありません。 すべてが良好で、この分解は安定し、常に最良の近似が存在します。 しかし、たとえばd = 10の場合、それを使用しようとすると、格納する必要がある補助的な2次元配列が存在し、弱体化された形式ではあるが、次元の呪いが残ります。



はい。たとえば、3次元から4次元の問題の場合、タッカー分解は非常に効果的です。 それが適用される作品はかなり多数あります。 それにもかかわらず、私たちの究極の目標はそれではありません。







デフォルトでは指数関数的な数のパラメーターはないが、すべてを計算できる場所を取得したい。 最初のアイデアは非常に単純でした。すべてがマトリックスに適している場合、テンソル、多次元配列からマトリックスをスカルプトしましょう。 どうやってやるの？ 簡単です。 d個のインデックスがあります。それらをグループに分け、マトリックスを作成し、分解をカウントしましょう。



壊れます。 インデックスの一部を小文字のインデックスとして宣言し、他の部分を列インデックスとして宣言します。 どういうわけか再配置。 MATLABおよびPythonでは、これはすべてreshapeおよびtransposeコマンドによって行われます。低ランクの近似を考慮します。 もう1つの質問は、その方法です。



当然、発生する小さな配列を再帰的に作成しようとすることができます。 単純な方法でそれらを作成すると、次の複雑さが生じることがわかり^ます 。r ^{log d} 。 もはや指数関数的ではありませんが、rは大幅に増加します。



これを慎重に行うと、1つのフレーズを言いますが、インデックスが1つ追加されます。 新しいインデックスと見なされる必要があります。 9次元の配列があり、インデックスを5 + 4に分割し、分解し、追加のインデックスを1つ、6次元と5次元のテンソルを1つ取得し、それらを分解し続けるとします。 この形式では、指数関数的な複雑さは発生せず、まさにそのような数のパラメーターを持つ表現が得られます。 そして、誰かが私たちに、道路で得られたすべての行列が低いランクを持っていると言ったとしたら？ このような再帰構造が判明しました。 それは非常に厄介で、プログラムするのは嫌です、私はそれをするのが面倒でした。







ある時点で、この構造の最も単純な形式を選択できることに気付きましたが、これは非常に強力です。 これがテンソルトレイン、テンソルトレインになりました。 私たちはこれを提案しました、名前は固まりました。 それから、もちろん、私たちはこれを思いついた最初の人ではないことがわかりました。 固体物理学では、行列積状態として知られていました。 しかし、良いことは少なくとも2回発見しなければならないことをすべての報告で繰り返します。さもなければ、それが良いかどうかはあまり明確ではありません。 少なくとも、このパフォーマンスは少なくとも2回、さらには2.5回、または3回も開かれました。



ここにアイデアがあります。私はこの6、7年の間、分解と研究に取り組んでおり、最後まで研究されたとは言えません。



テンソルは、1つのインデックスのみに依存するオブジェクトの積として表されます。 実際、変数の分離について話していますが、1つの小さな例外があります。これらの小さなものは行列です。 これらの行列を乗算して、ポイントテンソルの値を取得します。 最初の要素は行、次にマトリックス、マトリックス、列です-数値を取得します。 また、これらの行列はパラメーターに依存し、3次元テンソルとして保存できます。 マトリックスのコレクションがあり、最初にステッチのコレクションがあります。 私たちは、ここからゼロライン、ここから5番目のマトリックス、ここから3番目のマトリックスが必要であると単純に乗算します。 明らかに、要素の計算にはdr ^2の操作が必要です。 インデックス形式でも。 コンパクトな外観。



ほとんど何も変わらないように見えますが、実際には、このような表現は特異分解のすべての特性を保持します。 計算、直交化、および最適な近似を見つけることができます。 これは、すべてのテンソルのセットの低パラメータ多様体ですが、幸運であり、解決策がそれにある場合は、簡単に見つけることができます。







いくつかのプロパティがあります。 現在、複数のランクがあります。 マトリックス、列、または行には1つのランクしかありませんが、マトリックスのランクは同じであるため、幸運です。 テンソルには多くのランクがあります。 先頭の数字rは標準ランクです。 ここにランクd-1があります。 dごとに独自のランクがあり、多くのランクがあります。 それにもかかわらず、これらの複雑さを決定するすべてのランクと、そのような表現を格納するためのメモリは、少なくとも理論的には、いくつかのマトリックスのランク、いわゆるスイープとして計算できます。 多次元配列を取得し、それを行列に変換し、ランクを考慮します-そのようなランクには分解があります。



なぜこれがフォーマットと呼ばれるのですか？ オブジェクトがこの形式で保存されている場合、加算、乗算、ノルムの計算の代数演算は、形式を離れることなく直接実行できます。 この場合、とにかく何かが起こります。 たとえば、2つのテンソルを合計すると、結果のランクはランクの合計を超えなくなります。 反復プロセスでこれを何度も実行すると、dの依存性がrで線形および2次である場合でも、ランクは非常に大きくなります。 ランク100〜200で安全に作業できます。 クラスターの物理学者はランク4000〜5000で作業できますが、十分に大きな密度のマトリックスを保存する必要があるため、使用できなくなりました。



しかし、ランクを下げることができる非常にシンプルで美しい代数アルゴリズムがあります。 フラベニウスのノルムには許容できる精度があり、精度を与える最小ランクを見つけたいと思います。 しかし、私は同時にランクを下げています。 丸め。 浮動小数点数を使用する場合、100桁すべてを保存するわけではありません。 16桁だけ残します。 これらの行列のサイズなど、許容できる精度を与えるパラメーターを見つけます。 これを行う信頼性の高い堅牢なアルゴリズムがあります-MATLABまたはPythonで20〜30行かかります。



もう1つ美しいことがあります。 物理学者は彼女を確実に知りませんでした。 私はこの結果を誇りに思います、それは私の当時のチーフであるエフゲニー・エフゲニエヴィッチ・タルティシュニコフと私のものです。 与えられたテンソルがそのような構造を持っていることがわかっている場合、dnr ²要素から確実に復元できます。 つまり、すべての要素を計算せずに、少数の要素を調べて、基底を使用せずにテンソル全体を復元できます。 これは興味深い事実であり、行列の場合、知られているほど知られていません。 ランクrの行列d = 2があります。 r列とr行で復元できます。



このような多様性がある場合、ランクを制限して機能を最小化できます。 標準的な状況：要素にはアクセスできませんが、最小限に抑えたい特定の機能があります。 このため、示された制限で最適化する方法について、まったく別の研究ラインが発生します。 これは凸集合ではありませんが、別個の研究を必要とする多くの興味深いトポロジー特性を持っています。



最近、主に偏微分方程式から生じる問題について、ランクが必要な精度に応じて対数的に振る舞うという推定を最終的に証明することができます。 そのような表現が準最適である問題のクラス全体があります。







TTランクのカウント方法を見ていきましょう。 マトリックスを取得し、最初のk個のインデックスを行インデックス、最後のdkを列インデックスと見なします。 , . .



. , . . — d-1 , . , 10-6, .



d . — . , . 1010, 100100. , 1000010000, .







dnr ³ . , - .



. - 100 , 10 , .



. .







. , . . , , . . , .



r, r r , . , , , .



, , . , , . — , 5, 5 5 , .



, . , .



, , , . - . , . , , . . : , .



. , -, . , . , , . . , .



, , .



— , . , d-. d- , . . 2 ^d 2222. , . . , , , .



— , - , — , - .



. . , . , , , . — .



: ttpy Python TT-Toolbox MATLAB. , , , , . , , .



. , , , . , , - , . - . , : . 10 ^-6 10 ^-8 . — , — . — , . , , , . , , , - . 見てみましょう。



, - , . TensorFlow . , — , . - , . , , .



, . . 2 ⁶⁰ . . , n ³ , n = 2 ^d , 220, . 2222, 60- . .



, : 2 d, 60, , 50. , .



, . , , , , . .







, . TensorNet, , NIPS . , . , , .



. . , .



, . , , . , . , , : , .







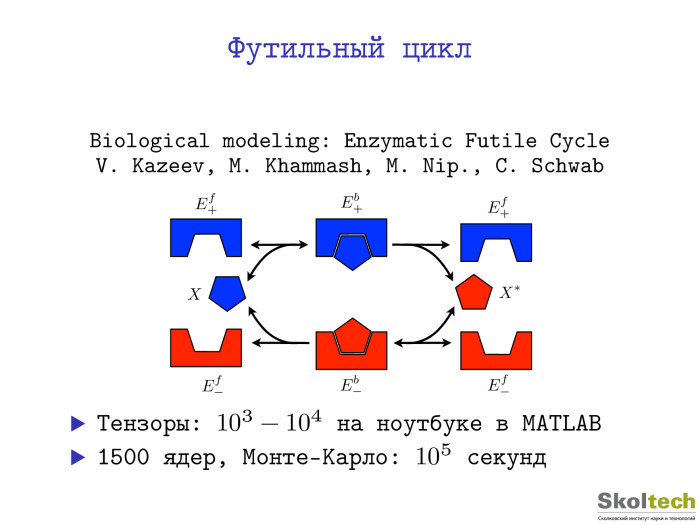
. : , , , , . , , . , . , — , . , . , , . -, . 1500 — 10 ⁵ . MATLAB . .







. 12 , 12- , 30 ¹² . .







Exponential Machines, x1, x2, , 2 ^d . 2222 : . 動作します。 , , .



. , , . , - — , . RecSys. Polara. , , . : . : , « », SVD « ». « » . . : « — » « — — » , . - . , , , - : , , , . , .







, — . . , deep learning. , arithmetic circuit. , .



, GitHub , . , .