ニューラルネットワークガイドの第2部へようこそ。 ずっと前に第2部を待っていたすべての人に謝罪したいだけです。 特定の理由で、私はそれを書くのを延期しなければなりませんでした。 実際、最初の記事にこのような需要があり、このトピックに非常に多くの人々が興味を持つことを期待していませんでした。 あなたのコメントを考慮に入れて、できるだけ多くの情報を提供すると同時に、最もわかりやすい表現方法を維持しようとします。 この記事では、ニューラルネットワークをトレーニング/トレーニングする方法（特に、バックプロパゲーション法）について説明します。何らかの理由で最初の部分を読んでいない場合は、それから始めることを強くお勧めします。 この記事を書く過程で、他の種類のニューラルネットワークとトレーニング方法についても話したいと思いましたが、それらについて書き始めると、これは私のプレゼンテーション方法に反することに気付きました。 できるだけ多くの情報を得るのが待ちきれないことを理解していますが、これらのトピックは非常に広範囲で詳細な分析が必要であり、私の主な仕事は表面的な説明を含む別の記事を書くことではなく、トピックのあらゆる側面をもたらし、記事をできるだけ簡単にすることですマスタリング。 私はまだプログラミング言語を使うことに頼らず、「指で」すべてを説明するので、「ぶらぶら」の愛好家を怒らせます。 はじめに、ニューラルネットワークの研究を続けましょう。

ニューロンバイアスとは

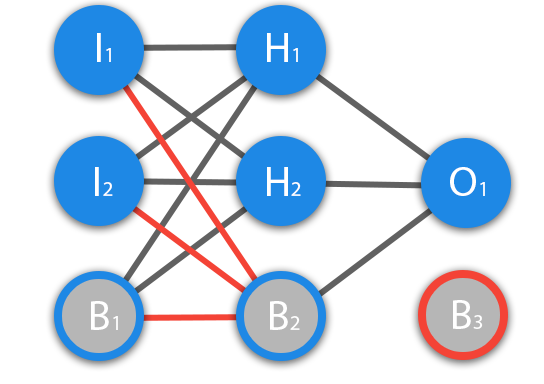
メイントピックを開始する前に、別の種類のニューロンの概念-変位ニューロンを紹介する必要があります。 変位ニューロンまたはバイアスニューロンは、ほとんどのニューラルネットワークで使用される3番目のタイプのニューロンです。 このタイプのニューロンの特徴は、入力と出力が常に1に等しく、入力シナプスがないことです。 変位ニューロンは、ニューラルネットワークに一度に1つずつ存在するか、完全に存在しないか、50/50は存在しません（配置できない赤の重みとニューロンは図に示されています）。 変位ニューロンの接続は、通常のニューロンの接続と同じです。次のレベルのすべてのニューロンは、2つのバイアスニューロン間にシナプスが存在できないことを除きます。 したがって、それらは入力レイヤーとすべての非表示レイヤーに配置できますが、出力レイヤーには配置できません。何も接続しないためです。

変位ニューロンとは何ですか？

バイアス関数は、活性化関数のグラフを右または左にシフトして出力を得るために必要です。 これがわかりにくい場合は、1つの入力ニューロンと1つの出力ニューロンがある単純な例を見てみましょう。 次に、出力O2が入力H1と等しくなり、その重みが乗算されて、アクティベーション関数（左の写真の式）を通過することが確認できます。 特定のケースでは、シグモイドを使用します。



数学の学校のコースから、関数y = ax + bを取り、その「a」値を変更すると、関数の傾き（左側のグラフの線の色）が変更され、「b」を変更するとシフトすることがわかります関数の左または右（右側のグラフの線の色）。 したがって、「a」はH1の重みであり、「b」は変位ニューロンB1の重みです。 これは大雑把な例ですが、このようなものは機能します（画像の右側のアクティベーション関数を見ると、式間の非常に強い類似性に気付くでしょう）。 つまり、トレーニング中に隠れニューロンと出力ニューロンの重みを調整すると、活性化関数の勾配が変化します。 ただし、変位ニューロンの重みを調整すると、X軸に沿って活性化関数をシフトし、新しい領域をキャプチャできる場合があります。 言い換えると、左のグラフに示すように、決定の原因となるポイントが見つかった場合、NSは変位ニューロンを使用しないと問題を解決できません。 したがって、変位ニューロンのないニューラルネットワークはほとんど見られません。



また、バイアスニューロンは、すべての入力ニューロンが0になり、その重みに関係なく、次のレイヤー0にすべて移行しますが、バイアスニューロンがある場合は役立ちます。 変位ニューロンの有無は、ハイパーパラメーターです（これについては後で詳しく説明します）。 つまり、変位ニューロンを使用する必要があるかどうかを自分で決定する必要があります。NSをニューロンを混合して、それらなしでNSを駆動し、結果を比較します。



変位ニューロンが回路上に表示されない場合があることを知っておくことは重要ですが 、入力値を計算するときは、たとえば次のように重みを考慮するだけです。



入力= H1 * w1 + H2 * w2 + b3

b3 =バイアス* w3



出力は常に1であるため、重み付きのシナプスが追加され、ニューロン自体に言及せずにこの重みを合計に追加することを単純に想像できます。

NAに正しい答えを出させる方法は？

答えは簡単です-彼女を訓練する必要があります。 ただし、答えがどれほど単純であっても、単純さの観点からの実装には多くの要望が残されています。 NAを教えるにはいくつかの方法がありますが、私の意見では、最も興味深いものを3つ強調します。

• バックプロパゲーション法
• 弾性伝播法（弾性伝播またはRprop）
• 遺伝的アルゴリズム

RpropとGAについては他の記事で説明しますが、ここでは基本の基礎である、勾配降下アルゴリズムを使用する逆伝播法について説明します。

勾配降下法とは何ですか？

これは、勾配に沿って移動することにより、関数の局所的な最小値または最大値を見つける方法です。 勾配降下法の本質を理解している場合、逆伝播法を使用する際に質問はありません。 そもそも、勾配とは何か、そして国会のどこに勾配があるのか​​を理解しましょう。 x軸に沿ってニューロンの重みの値（w）があり、y軸に沿ってこの重みに対応するエラー（e）があるグラフを作成しましょう。









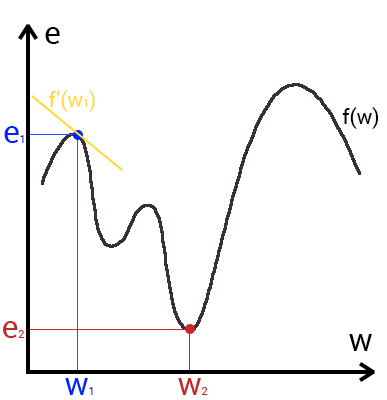
このグラフを見ると、関数f（w）のグラフは、選択した重みに対する誤差の依存性であることがわかります。 このグラフでは、グローバルな最小値-ポイント（w2、e2）、つまり、グラフがx軸に最も適合する場所に興味があります。 この点は、重みw2を選択すると、最小のエラーe2が得られることを意味し、その結果、可能な限り最高の結果になります。 勾配降下法は、このポイントを見つけるのに役立ちます（勾配はグラフの黄色で示されます）。 したがって、ニューラルネットワークの各重みには独自のスケジュールと勾配があり、それぞれにグローバルな最小値を見つける必要があります。



それでは、この勾配は何ですか？ 勾配は、勾配の急峻さを決定するベクトルであり、表面またはグラフ上の任意の点に対するその方向を示します。 勾配を見つけるには、特定のポイントでグラフの導関数を取得する必要があります（グラフに示されているように）。 この勾配の方向に移動すると、低地にスムーズに滑り込みます。 ここで、エラーがスキーヤーであり、関数グラフが山であると想像してください。 したがって、エラーが100％の場合、スキーヤーは山の最上部におり、エラーが0％の場合、低地にいます。 すべてのスキーヤーと同様に、間違いは階下に行き、その価値をできる限り早く減らす傾向があります。 最終的に、次の結果が得られます。









スキーヤーがヘリコプターを使用して山に投げられていると想像してください。 どのくらい高いか低いかは、ケースに依存します（初期化中にニューラルネットワークで重みがランダムな順序で配置される方法と同様）。 エラーが90％であり、これが出発点であるとしましょう。 ここで、スキーヤーは勾配を使用して下降する必要があります。 途中で勾配を計算し、勾配の方向を示し、勾配が変わったらそれを調整します。 傾斜がまっすぐな場合、そのようなアクションのn番目の数の後、低地に到達します。 しかし、ほとんどの場合、斜面（関数グラフ）は波状になり、スキーヤーは非常に深刻な問題に直面します-極小値。 メモリの更新のために、ローカルおよびグローバルな関数の最小値が何であるかは誰もが知っていると思います。 ここに例を示します。 ローカルミニマムを打つことは、私たちのスキーヤーがこの低地に永遠に留まり、決して山を滑り落ちることはないという事実に満ちているため、正しい答えを得ることができません。 ただし、スキーヤーにモーメンタムと呼ばれるジェットパックを装備することで、これを回避できます。 以下はその瞬間の簡単な説明です。







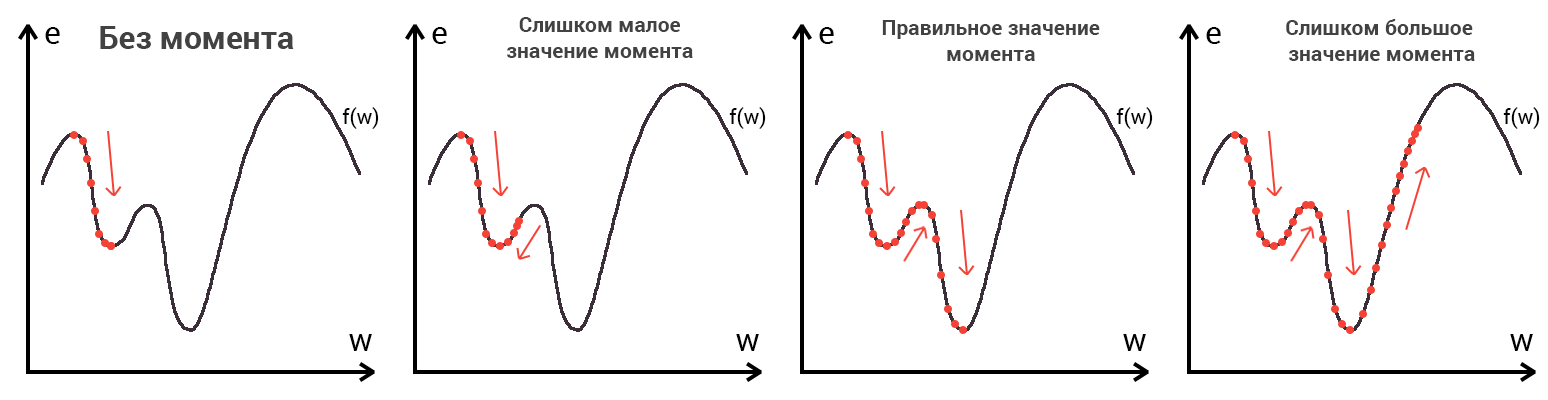
おそらく既にご想像のとおり、このランドセルは、スキーヤーに必要な加速を与え、丘を乗り越えて私たちを最小限に抑えますが、1つあります。 モーメントパラメータに特定の値を設定し、すべてのローカルの低値を簡単に克服してグローバルな最小値に到達できたと想像してください。 ジェットパックをオフにすることはできないため、隣に低地がまだある場合、グローバルミニマムをすり抜けることができます。 最後のケースでは、遅かれ早かれ、いずれにせよグローバルミニマムに戻るので、これはそれほど重要ではありませんが、瞬間が大きいほど、低地でスキーヤーが乗る範囲が大きくなることを覚えておく価値があります。 瞬間とともに、逆伝播法は学習率などのパラメーターも使用します。 おそらく多くの人が考えるように、学習速度が速いほど、ニューラルネットワークのトレーニングが速くなります。 いや 学習の速度と瞬間は、ハイパーパラメーターであり、試行錯誤によって選択される値です。 トレーニングの速度は、スキーヤーの速度に直接関係する可能性があり、静かに歩き続けることが確実であると言えます。 ただし、スキーヤーに速度をまったく与えない場合、彼はどこにも行かないため、特定の側面もあります。低速にすると、移動時間が非常に長い間続く可能性があります。 速度を上げすぎるとどうなりますか？









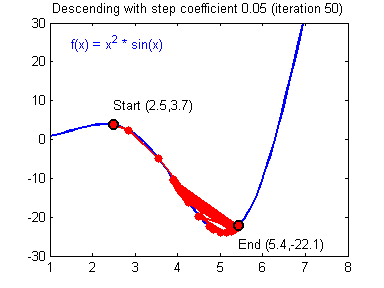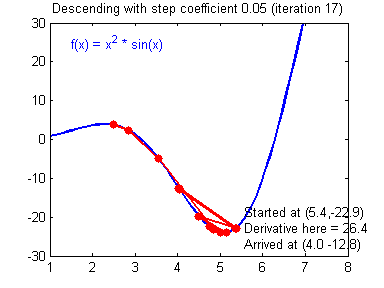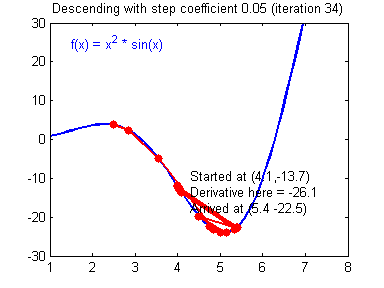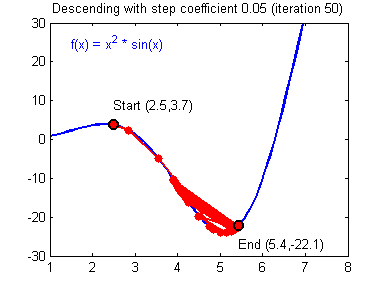
ご覧のとおり、良いことは何もありません。 スキーヤーは間違った道を滑り始め、おそらく他の方向に滑り出します。これは、ご存じのとおり、正しい答えを見つけるまでの距離を縮めるだけです。 したがって、これらすべてのパラメーターでは、NSの収束を回避するために中間点を見つける必要があります（これについては後で説明します）。

逆伝播法（MPA）とは何ですか？

ですから、国会が適切に学習し、正しい決定を下せるように、それをどうやって作るかを議論できるようになりました。 このGIFでは、非常に優れたMPAが視覚化されています。







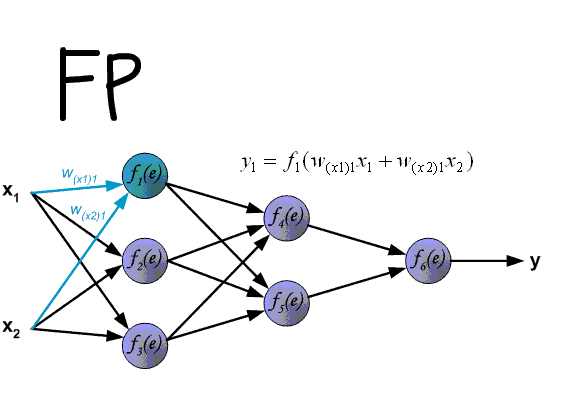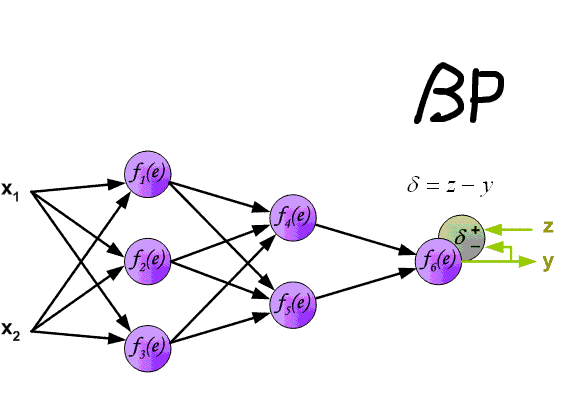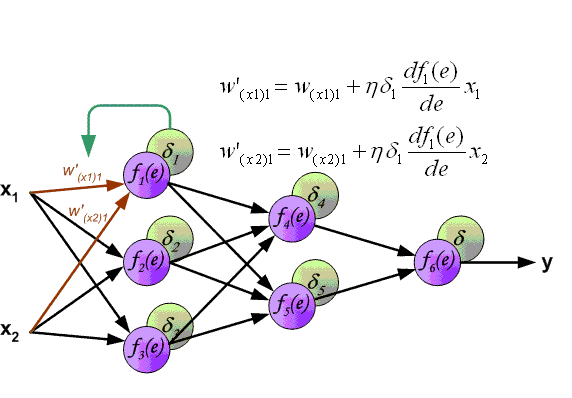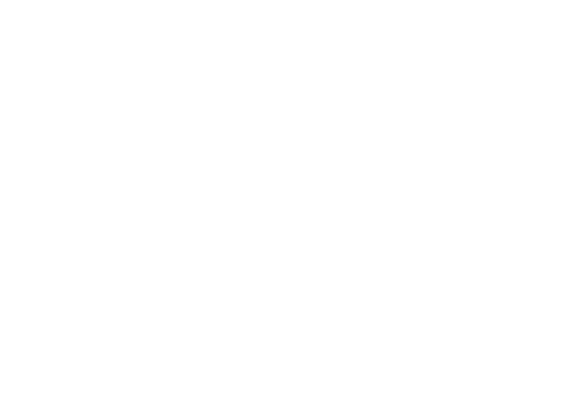
それでは、各ステップを詳しく見ていきましょう。 覚えているなら、前の記事で、我々は国会の終了を検討した。 別の方法では、これはForward Passと呼ばれます。つまり、入力ニューロンから出力ニューロンに情報を順次送信します。 その後、エラーを計算し、それに基づいて逆方向の送信を行います。これは、出力ニューロンの重みから始めて、ニューラルネットワークの重みを順次変更することで構成されます。 スケールの値は、最良の結果が得られる方向に変化します。 私の計算では、デルタを見つける方法を使用します。これは最も簡単で理解しやすい方法だからです。 また、重みを更新する確率論的な方法も使用します（これについては後で説明します）。



前の記事で計算を終了したところから続けましょう。





すでに国会の結果とその誤差を計算しているので、すぐにMPAに進むことができます。 前述したように、アルゴリズムは常に出力ニューロンで始まります。 この場合、式1に従ってδ（デルタ）の値を計算してみましょう。

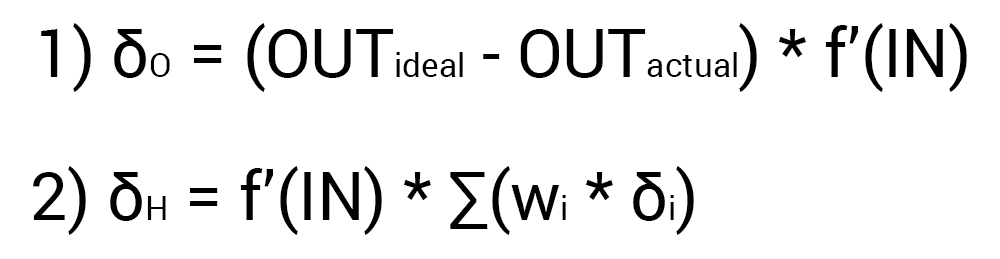出力ニューロンには出力シナプスがないため、最初の式（δ出力）を使用します。したがって、非表示のニューロンについては、すでに2番目の式（δhidden）を使用します。 ここではすべてが非常に簡単です。目的の結果と取得した結果の違いを考慮し、このニューロンの入力値からの活性化関数の微分を掛けます。 計算を進める前に、デリバティブに注意を向けたいと思います。 まず、おそらく既に明らかになっているように、MPAでは、区別できるアクティベーション機能のみを使用する必要があります。 第二に、不必要な計算を行わないために、導関数式は、よりフレンドリーでシンプルな形式の式に置き換えることができます。



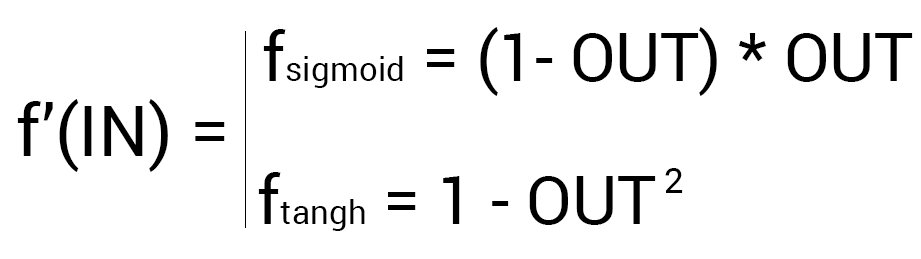
したがって、ポイントO1の計算は次のようになります。





これで、O1ニューロンの計算が完了しました。 ニューロンのデルタをカウントした後、このニューロンのすべての出力シナプスの重みをすぐに更新する必要があることに注意してください。 O1の場合はそうではないので、隠れレベルのニューロンに行き、2番目のデルタ計算式があり、その本質は活性化関数の微分を入力値からすべての積の合計で乗算することを除いて同じことを行います発信の重みと、このシナプスが関連付けられているニューロンのデルタ。 しかし、なぜ式が違うのですか？ 実際、MPAの本質は、出力ニューロンの誤差をNSのすべての重みに分散させることです。 エラーは出力レベルでのみ計算できます。すでに行ったように、このエラーが既に存在するデルタも計算しました。 そのため、ここではエラーの代わりにデルタを使用します。これは、ニューロンからニューロンに送信されます。 この場合、H1のデルタを見つけましょう。





次に、各出力シナプスの勾配を見つける必要があります。 通常、3階建ての分数と多くの導関数やその他の数学的な地獄を挿入しますが、それはデルタをカウントする方法を使用することの魅力です。最終的に勾配を見つけるための式は次のようになります。



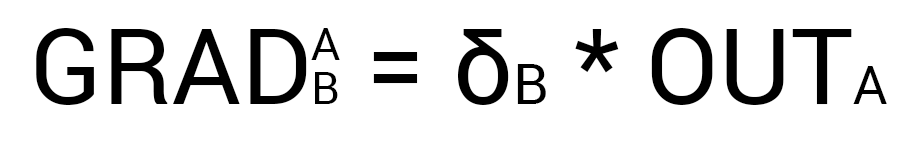
ここで、ポイントAはシナプスの開始点、ポイントBはシナプスの終了点です。 したがって、次のようにw5の勾配を計算できます。





これで、w5の重みを更新するために必要なすべてのデータが得られました。これは、1つまたは別の重みを変更する必要がある値を計算するMPA関数のおかげです。



式の2番目の部分を無視せず、瞬間を使用することを強くお勧めします。これにより、ローカルミニマムの問題を回避できます。



ここでは、勾配降下アルゴリズムを検討したときに既に述べた2つの定数があります。E（イプシロン）-学習速度、α（アルファ）-モーメントです。 数式を単語に変換すると、シナプスの重みの変化は、学習速度の係数にこの重みの勾配を乗じたものに等しくなり、この重みの前の変化を掛けたモーメントが加算されます（最初の反復では0です）。 この場合、重みw5の変化を計算し、それにΔw5を追加してその値を更新しましょう。





したがって、アルゴリズムを適用すると、重量が0.063増加しました。 H2についても同じことを行うことをお勧めします。





もちろん、I1とI2についても忘れないでください。これらのシナプスにも更新する必要がある重みがあります。 ただし、入力ニューロンには入力シナプスがないため、入力ニューロンのデルタを見つける必要はありません。





それでは、すべてを正しく行ったことを確認しましょう。更新された重みのみを使用して、国会の出力を計算します。





MPAを1回繰り返した後、0.04（6％）の誤差を減らすことができました。 エラーが十分に小さくなるまで、これを何度も繰り返す必要があります。

学習プロセスについて他に何を知る必要がありますか？

ニューラルネットワークは、教師ありでも教師なしでも教えることができます（教師あり、教師なし学習）。



教師による指導は、回帰や分類などの問題に固有のトレーニングの一種です（上記の例で使用しました）。 つまり、ここであなたは教師として、国会は学生として行動します。 入力データと希望する結果を提供します。つまり、入力を見ている学生は、提供した結果を得るために努力する必要があることを理解します。



教師なしで学習-このタイプの学習はそれほど一般的ではありません。 教師がいないので、ネットワークは希望する結果を得られないか、その数が非常に少ないです。 基本的に、このタイプのトレーニングは、特定のパラメーターに従ってデータをグループ化するタスクであるNSに固有のものです。 ハブで10,000件の記事を提出し、これらすべての記事を分析した後、国会は、たとえば頻繁に発生する単語に基づいてそれらを分類できるとします。 プログラミング言語、プログラミング、およびPhotoshopのような言葉がデザインする場所について言及している記事。



強化学習のような興味深い方法がまだあります。 この方法は別の記事に値しますが、その本質を簡単に説明しようとします。 この方法は、国会から得られた結果に基づいて、推定値を与えることができる場合に適用できます。 たとえば、PAC-MANをプレイするように国会に教えたいと思っています。国会が多くのポイントを獲得するたびに、それを奨励します。 いいかえれば、私たちは、良い結果が得られる限り、目標を達成する方法を見つける権利を国会に与えます。 このようにして、ネットワークは彼らがそれから何を達成したいのかを理解し始め、「教師」によるデータの絶え間ない提供なしでこの目標を達成するための最良の方法を見つけようとしています。



また、トレーニングは3つの方法で行うことができます：確率的方法（確率的）、バッチ法（バッチ）およびミニバッチ法（ミニバッチ）。 どちらの方法が優れているかについての多くの記事や研究があり、誰もが共通の答えを得ることができません。 私は確率論的手法の支持者ですが、各手法に長所と短所があるという事実を否定しません。



各方法の概要：



確率的 （オンラインとも呼ばれる）方法は、次の原則に従って動作します-Δwが見つかり、対応する重みを即座に更新します。



バッチ方式の動作は異なります。 現在の反復でのすべての重みのΔwを集計し、この合計を使用してすべての重みを更新します。 このアプローチの最も重要な利点の1つは、計算時間を大幅に節約できることですが、この場合の精度は大幅に低下する可能性があります。



ミニバッチ法は黄金の平均であり、両方の方法の利点を組み合わせようとしています。 ここでは、原則は次のとおりです。重みをグループに自由に配分し、特定のグループ内のすべての重みの合計Δwによって重みを変更します。

ハイパーパラメーターとは何ですか？

ハイパーパラメーターは、試行錯誤によって手動で、そして多くの場合選択する必要がある値です。 これらの値の中で、以下を区別できます。

• トレーニングの瞬間とスピード
• 隠れ層の数
• 各層のニューロンの数
• 変位ニューロンの有無

他のタイプのNSでは、追加のハイパーパラメーターが存在しますが、それらについては説明しません。 適切なハイパーパラメータの選択は非常に重要であり、NSの収束に直接影響します。 変位ニューロンを使用する価値があるかどうかを理解するのは非常に簡単です。 隠れ層とその中のニューロンの数は、1つの単純なルールに基づく徹底的な検索によって計算できます。ニューロンが多いほど、結果の精度が上がり、トレーニングに費やす時間が指数関数的に長くなります。 ただし、単純な問題を解決するために、1000個のニューロンでNSを作成しないでください。 しかし、学習の瞬間と速度を選択すると、すべてが少し複雑になります。 これらのハイパーパラメーターは、国​​会のタスクとアーキテクチャに応じて異なります。 たとえば、XORソリューションの場合、学習速度は0.3〜0.7の範囲になりますが、株価を分析および予測するNAでは、0.00001を超える学習速度はNSの収束が不十分になります。 ハイパーパラメーターに注意を集中せず、それらの選択方法を完全に理解しようとしないでください。 これには経験が伴いますが、今のところは、ネットワーク上の特定の問題に対する解決策の例を単純に実験して探すことをお勧めします。

収束とは何ですか？

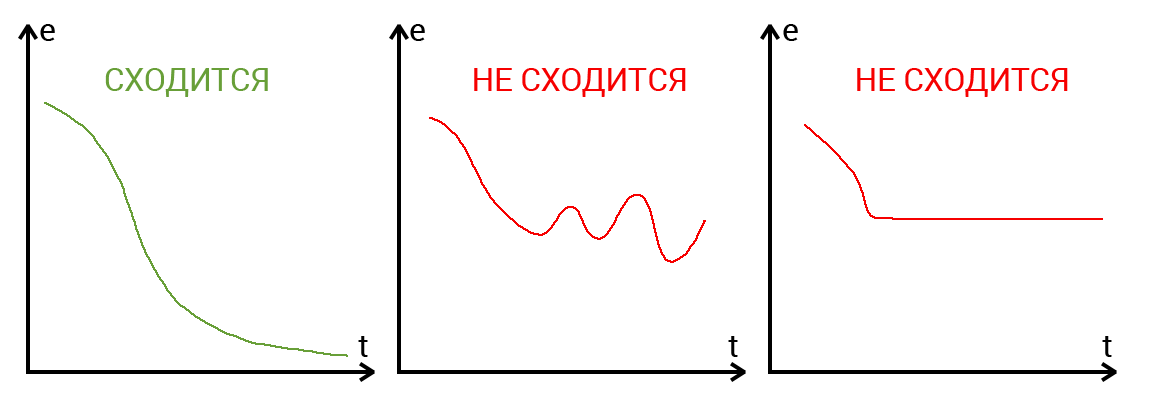
収束は、NSアーキテクチャが正しいかどうか、タスクに従ってハイパーパラメーターが正しく選択されたかどうかを示します。 プログラムがログの各反復でNSエラーを表示するとします。 エラーが反復ごとに減少する場合、正しい軌道に乗っており、NSが収束します。 エラーが特定のレベルで上下する、またはフリーズする場合、国会は収束しません。 99％のケースでは、これはハイパーパラメーターを変更することで解決されます。 残りの1％は、国会の構造に誤りがあることを意味します。 NSの再トレーニングによって収束が影響を受けることも起こります。

再トレーニングとは何ですか？

名前が示すように、再トレーニングは、データで飽和状態になったときのニューラルネットワークの状態です。 この問題は、ネットワークが同じデータで長時間トレーニングされている場合に発生します。 つまり、ネットワークはデータから学習するのではなく、データを記憶して「詰め込む」ようになります。 したがって、このNSの入力に新しいデータを送信しようとすると、受信したデータにノイズが表示され、結果の精度に影響を与える可能性があります。 たとえば、リンゴの異なる写真（赤い写真のみ）を表示して、それがリンゴだと言う場合。 そして、国会が黄色または緑のリンゴを見ると、すべてのリンゴは赤であることを覚えていたため、それがリンゴであると判断することはできません。 そしてその逆に、国会が赤いものを見て桃のようなリンゴの形に一致すると、彼女はそれがリンゴだと言うでしょう。 これがノイズです。 グラフでは、ノイズは次のようになります。









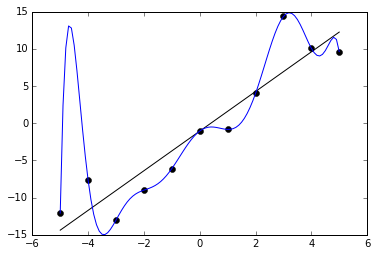
関数のグラフは、NSの出力（結果）であるポイントごとに大きく異なることがわかります。 理想的には、このグラフは波状でなく、直線である必要があります。 再トレーニングを回避するために、同じまたは非常に類似したデータでNSを長時間トレーニングしないでください。 また、再トレーニングは、NSの入力または複雑すぎるアーキテクチャに入力する多数のパラメーターによって引き起こされる可能性があります。 したがって、トレーニングフェーズの後に出力でエラー（ノイズ）に気付いた場合は、いずれかの正則化方法を使用する必要がありますが、ほとんどの場合、これは必要ありません。

おわりに

この記事が、ニューラルネットワークのような難しい主題の重要なポイントを明確にしたことを願っています。 しかし、どれだけ多くの記事を読んだとしても、このような複雑なトピックを実践せずに習得することは不可能だと思います。 したがって、あなたが道の始まりに過ぎず、この有望で発展途上の業界を探求したい場合は、独自のNSの作成を練習し、その後、さまざまなフレームワークとライブラリの助けに頼ることをお勧めします。 また、情報を提示する私の方法に興味があり、機械学習に関連する他のトピックに関する記事を書きたい場合は、興味のあるトピックについて下の投票に投票してください。 今後の記事でお会いしましょう:)