入学のために、いくつかの段階を経て、論理的/数学的問題を解決することが提案されました。
この記事の第1段階の典型的な問題を解決するためのオプションを作成してみます。
PS:カウントコードをすばやく記述してデバッグするために、JavaScriptが使用されました。
記事を書いている間、私はサンドボックスでトピックの前にすでにいたように見えます。 しかし、私は他のタイプのタスクを検討しましたが、程度については1つだけが一致しました(ただし、コメントによって判断すると、著者への違反はありません-解決策は間違っています)。
代替ソリューションに関するコメントや提案を歓迎します。
タスク1
中央の1から始まり、5 x 5の螺旋が得られるまで数字を時計回りに順番に並べる螺旋を考えます。
対角線上のすべての数値の合計が101であることを確認できます。
1195年から1195年までのスパイラルの対角線上の数字の合計はどうなりますか?
解決策1
真ん中かららせん状に進み、角の数字を単純に要約します:1 + 3 + 5 + 7 + 9 + 13 + 17 + 21 + 25 + ...
このシーケンスでは、後続の各番号がデルタd (最初は2、3、5、7、9に等しい)だけ異なることに気付くかもしれません。 この場合、スパイラルの次のラウンドへの移行ごとに、4つの角数間のデルタがさらに2、13、17、21、25増加します。
1回転の角数の合計は次の式で計算されます: (v + d)+(v + 2 * d)+(v + 3 * d)+(v + 4 * d) 、ここでvは前の回転の最後の数(1 、9、25、...)、 d-デルタ。 デルタdをらせんサイズのサイズまで増加させることにより、サイクルを構築します。
コメントでeandr_67によって提案された2次シーケンスの合計のような代替ソリューション:
サイズ = 1195のスパイラルの場合、対角線上の数字の合計は1138375521です。
解決策1
真ん中かららせん状に進み、角の数字を単純に要約します:1 + 3 + 5 + 7 + 9 + 13 + 17 + 21 + 25 + ...
このシーケンスでは、後続の各番号がデルタd (最初は2、3、5、7、9に等しい)だけ異なることに気付くかもしれません。 この場合、スパイラルの次のラウンドへの移行ごとに、4つの角数間のデルタがさらに2、13、17、21、25増加します。
1回転の角数の合計は次の式で計算されます: (v + d)+(v + 2 * d)+(v + 3 * d)+(v + 4 * d) 、ここでvは前の回転の最後の数(1 、9、25、...)、 d-デルタ。 デルタdをらせんサイズのサイズまで増加させることにより、サイクルを構築します。
function task1(size) { for (var v=1, d=2, sum=v; d<size; v+=4*d, d+=2) { sum += 4*v+10*d; } return sum; }
コメントでeandr_67によって提案された2次シーケンスの合計のような代替ソリューション:
function task1_alt(size) { return (size * size * size * 2 / 3.0 + size * size / 2.0 + size * 4 / 3.0 - 1.5); }
サイズ = 1195のスパイラルの場合、対角線上の数字の合計は1138375521です。
タスク2
関数P(n、k)を次のように定義します:nがk個の素数の合計として表現できる場合、P(n、k)= 1(レコード内の素数を繰り返すことができ、1は素数ではありません)およびP(n、 k)= 0の反対の場合。
たとえば、P(10.2)= 1 10は、3 + 7または5 + 5、およびP(11,2)= 0の合計として表すことができます。2つの素数が合計11を与えることはできないからです。
関数S(n)は、1 <= i <= n、1 <= k <= nとなるように、すべてのiとkに対する関数P(i、k)の値の合計として定義します。
したがって、S(2)= P(1,1)+ P(2,1)+ P(1,2)+ P(2,2)= 1、S(10)= 20、S(1000)= 248838。
S(17688)を見つけます。
決定2
プライムのプロパティを使用します。
k> 3の場合、関数P(i、k)の値は、前のステートメントからの結果として入力されます。 さらに、すべての偶数i> = 4は、最大k = i / 2個の素数に分解できます(奇数の場合はk = i / 2-1)。
視覚行列を作成します。ここで、iは1〜nの数値で、k個の素数の合計に分解できます。
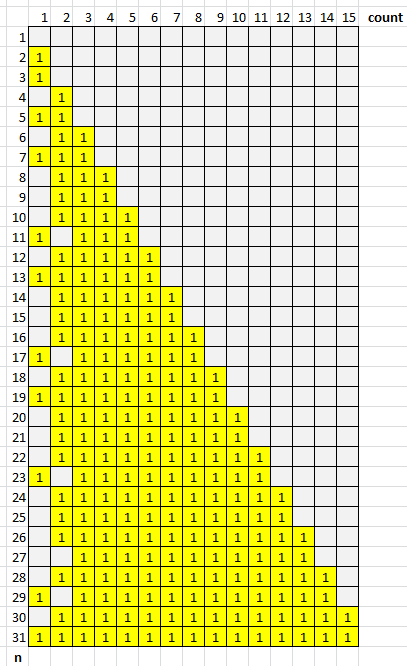
素数ではない奇数があり、同時に2つの素数の合計として表すことができないことに気付くかもしれません-この場合、例えば27 。
素数の数は、以前に取得したすべての素数の剰余なしのモジュロ除算により、奇数をチェックすることで計算できます。
合計カウント関数S(n):
S(17688)= 78193870。
決定2
プライムのプロパティを使用します。
- 2より大きい各偶数は、2つの素数の合計として表すことができます。 (2012年のGoldbachバイナリ問題(またはオイラー問題)は 、4×10 18を超えないすべての偶数についてチェックされます)
- 5より大きい各奇数は、3つの素数の合計として表すことができます。 ( ゴールドバッハの三項問題 、2013年に証明)
k> 3の場合、関数P(i、k)の値は、前のステートメントからの結果として入力されます。 さらに、すべての偶数i> = 4は、最大k = i / 2個の素数に分解できます(奇数の場合はk = i / 2-1)。
視覚行列を作成します。ここで、iは1〜nの数値で、k個の素数の合計に分解できます。
素数ではない奇数があり、同時に2つの素数の合計として表すことができないことに気付くかもしれません-この場合、例えば27 。
素数の数は、以前に取得したすべての素数の剰余なしのモジュロ除算により、奇数をチェックすることで計算できます。
// function isPrime(x,primes){ for (var j=0, len=primes.length; j<len; j++){ if (x%primes[j]==0) return false; } return true; }
合計カウント関数S(n):
function task2(n) { for (var i=4, count=2, primes=[2,3]; i<=n; i++){ // - if (i%2==0) { count+=i/2-1; } else { // count+=(i-1)/2-1; // if (i!=(primes[primes.length-1]+2)) { count--; } // - if (isPrime(i,primes)) { count++; // primes[primes.length]=i; } } } return count; }
S(17688)= 78193870。
タスク3
番号125874とそれに2-251748を掛けた結果は、番号を並べ替えることで相互に取得できます。 数値を並べ替えることにより、数値2 * x、3 * xが互いに得られるような最小の正の整数xを見つけます。
決定3
数字を並べ替えて数字を簡単に比較するために、数字を昇順の記号で行に入れます。
そして、これらの行を順序付けられたxと比較します。
コメントでは、 Largeは検索xから除外することを提案しました。最初の数字は4以上です:412、5230、60457 ... 掛けるとき、数の長さは増加します-そして、そのようなxをチェックすることは意味がありません。
最初の桁xの最大値xFirstMaxを、 9の丸められた整数除算の結果と最大値aおよびbとして設定します。
最小の正の整数x = 142857( a = 2およびb = 3: a * x = 285714およびb * x = 428571の場合)。
決定3
数字を並べ替えて数字を簡単に比較するために、数字を昇順の記号で行に入れます。
// function sortVal(val) { var str=val.toString(); if (str.length>1){ return str.split("").sort().join(""); } else { return str; } }
そして、これらの行を順序付けられたxと比較します。
コメントでは、 Largeは検索xから除外することを提案しました。最初の数字は4以上です:412、5230、60457 ... 掛けるとき、数の長さは増加します-そして、そのようなxをチェックすることは意味がありません。
最初の桁xの最大値xFirstMaxを、 9の丸められた整数除算の結果と最大値aおよびbとして設定します。
function task3(a,b) { // x x var xFirstMax = Math.floor(9/Math.max(a,b)); for (var x=1, xSorted=''; x<=1000000; x++){ // x, if (x.toString()[0]>xFirstMax) continue; // x xSorted=sortVal(x); // x a b if (xSorted==sortVal(a*x) && xSorted==sortVal(b*x)) { var founded=x; break; } } return founded; }
最小の正の整数x = 142857( a = 2およびb = 3: a * x = 285714およびb * x = 428571の場合)。
タスク4
47を取り、裏返して追加すると、47 + 74 = 121-パリンドローム番号が得られます。
349を使用してこの操作を3回実行すると、回文も発生します。
349 + 943 = 1292
1292 + 2921 = 4213
4213 + 3124 = 7337
説明された操作の50回以下のアプリケーションでパリンドロームを取得できないように、13110未満の正の自然数の数を見つけます(操作は少なくとも1回適用する必要があります)。
決定4
50の直接的な合計操作は非常に大きな数につながる可能性があり、 Steletがコメントで示唆したように、予期しない結果になる可能性があります。 したがって、数字を文字列として保存します。 また、複数のフリップの代わりに、単純にペアの端から始まる番号の番号を要約します。これは、番号とその反転コピーの合計に相当します。
そしてすでに回文をチェックするために、受信した行を回して値をそれ自身と比較するのに十分です:7337 == reverse (7337)。
その結果、 maxNum = 13110未満の正の自然数の数は、50回の操作でそれらから回文を取得できないほどです:359。
決定4
50の直接的な合計操作は非常に大きな数につながる可能性があり、 Steletがコメントで示唆したように、予期しない結果になる可能性があります。 したがって、数字を文字列として保存します。 また、複数のフリップの代わりに、単純にペアの端から始まる番号の番号を要約します。これは、番号とその反転コピーの合計に相当します。
そしてすでに回文をチェックするために、受信した行を回して値をそれ自身と比較するのに十分です:7337 == reverse (7337)。
function task4(maxNum) { for (var num=1, count=0; num<maxNum; num++){ // 50 for (var op = 1, val=num, palindrome=false; op<=50; op++) { val=val.toString(); // , for (var iMax=val.length-1, i=iMax, j=0, digSum=0, arrSum=[], carry=0; i>=0 && j<=iMax; i--, j++) { // + digSum = parseInt(val[i])+parseInt(val[j])+carry; // 9 if (digSum>9) { // 10 arrSum[arrSum.length]=digSum-10; // carry=1; // if (i==0) arrSum[arrSum.length]=1; } else { arrSum[arrSum.length]=digSum; carry=0; } } val = arrSum.join(""); // if (val == val.split("").reverse().join("")) { // - palindrome = true; break; } } // - if (!palindrome) { count++; } } return count; }
その結果、 maxNum = 13110未満の正の自然数の数は、50回の操作でそれらから回文を取得できないほどです:359。
タスク5
1 <a <6および1 <b <6のすべての可能な数a bを考慮します。
2 2 = 4、2 3 = 8、2 4 = 16、2 5 = 32 3 2 = 9、3 3 = 27、3 4 = 81、3 5 = 243、4 2 = 16、4 3 = 64、4 4 = 256、4 5 = 1024、5 2 = 25、5 3 = 125、5 4 = 625、5 5 = 3125
繰り返しを削除すると、15の異なる数値が得られます。
2 <a <149および2 <b <121の異なる数a bはいくつですか?
決定5
上記の例では、オプション2 4 = 16と4 2 = 16が一致しました。 4 2は(2 * 2) 2 => 2 2 * 2 => 2 4と表すことができます。 したがって、すべてを累乗しないようにするために、たとえば、すべてを素数の累乗にすることができます。たとえば、16 = 2 4、27 = 3 3、125 = 5 3などです。
計算に必要な一連の素数は、上記の問題2の関数によって決定できますが、この場合の簡略化のために、既製の値を使用します。 さらに、最初の数個(2、3、5、7、11)を取るだけで十分です。最大素数はaの平方根以下になります。 この場合、<149を13度に分解することはできません:13 2 > 149。
一連の素数を調べて、次数で数aを表現できるかどうかを判断します。 そして、取得した次数に対応するbを掛けるだけです。 結果から、次のように、すべてのバリエーションa b ( arr )の配列に次の連想インデックスidxを設定します。
3 100 => a 3 b 100
および9 50 => 3 2 * 50 => 3 100 => a 3 b 100
したがって、 arr配列内の特定のインデックスを持つ要素の存在を確認します。
最終的なカウント関数。a1 、 b1は入力値の対応する最小値、 a2 、 b2は入力値の最大値です。
2 <a <149および2 <b <121の異なる数a bの場合 :16529。
決定5
上記の例では、オプション2 4 = 16と4 2 = 16が一致しました。 4 2は(2 * 2) 2 => 2 2 * 2 => 2 4と表すことができます。 したがって、すべてを累乗しないようにするために、たとえば、すべてを素数の累乗にすることができます。たとえば、16 = 2 4、27 = 3 3、125 = 5 3などです。
// function isPowerOf(val,prime){ var power = 0; // if (val%prime == 0) { // while ((val/=prime)>=1) { power++; if (val==1) return power; } } return 0; }
計算に必要な一連の素数は、上記の問題2の関数によって決定できますが、この場合の簡略化のために、既製の値を使用します。 さらに、最初の数個(2、3、5、7、11)を取るだけで十分です。最大素数はaの平方根以下になります。 この場合、<149を13度に分解することはできません:13 2 > 149。
一連の素数を調べて、次数で数aを表現できるかどうかを判断します。 そして、取得した次数に対応するbを掛けるだけです。 結果から、次のように、すべてのバリエーションa b ( arr )の配列に次の連想インデックスidxを設定します。
3 100 => a 3 b 100
および9 50 => 3 2 * 50 => 3 100 => a 3 b 100
したがって、 arr配列内の特定のインデックスを持つ要素の存在を確認します。
最終的なカウント関数。a1 、 b1は入力値の対応する最小値、 a2 、 b2は入力値の最大値です。
// a1, b1 - , a2, b2 - function task5(a1,a2,b1,b2) { for (var a=a1+1, arr=[], power=1, count=0; a<a2; a++){ // var primes = [2,3,5,7,11]; // , , for (var i=0; i < primes.length; i++) { power = isPowerOf(a,primes[i]); if (power>1) { break; } } for (var b=b1+1, idx=''; b<b2; b++){ // a b idx = (power>1)? "a"+primes[i]+"b"+power*b : "a"+a+"b"+b ; // if (!arr[idx]) { // arr[idx]=1; // count++; } } } return count; }
2 <a <149および2 <b <121の異なる数a bの場合 :16529。
タスク6
いくつかの数字では、合計10までの数字のシーケンスを見つけることができます。たとえば、3523014には、次の4つのシーケンスがあります。
352 3014
3 523 014
3 5230 14
35 23014
あなたはそのような素晴らしい数字を見つけることができ、その数字はそれぞれ少なくとも1つのそのようなシーケンスに含まれています。
たとえば、3523014は素晴らしい数字であり、28546はそうではありません(合計10を与える数字のシーケンスがなく、同時に5を含む)。
区間[1、1900000](両方の境界を含む)でこれらの顕著な数の数を見つけます。
決定6
この問題の唯一の解決策は、直接検索することでした。 しかし、できる限り最適化しようとしました。
各数字numは、数字の配列arrPrepに分割され、そこからすべてのゼロが除外されます。 それらは何の役割も果たしません。
まず、すべての数字の合計を一度に確認できます。
次に、最初の2桁と最後の2桁をすぐに確認できます。 合計で少なくとも1つのペアが10より大きい場合、その数は間違いなく素晴らしいものではありません。たとえば、 56 112、1273 79です。
これで、すべてのシーケンスのソートを開始できます。
シーケンスの合計は、2次元配列sに書き込まれます。 主対角線にはarrPrepのすべての数値が事前に入力されています。
成功したシーケンスが見つかった場合、 arrCheck検証配列にこのシーケンスの番号を入力します。
最後に、arrPrep配列とarrCheck検証配列の文字列表現を比較します。 それらが等しい場合、数字のすべての数字が少なくとも1つの成功したシーケンスで使用されます-つまり 数は素晴らしいです。
間隔[1、1900000]の顕著な数:152409。
決定6
この問題の唯一の解決策は、直接検索することでした。 しかし、できる限り最適化しようとしました。
各数字numは、数字の配列arrPrepに分割され、そこからすべてのゼロが除外されます。 それらは何の役割も果たしません。
まず、すべての数字の合計を一度に確認できます。
- 10に等しい場合-すなわち 番号は最大のシーケンスであり、すぐに素晴らしいと考えられます。
- 10未満の場合-番号には順序がなく、素晴らしいものではありません。
次に、最初の2桁と最後の2桁をすぐに確認できます。 合計で少なくとも1つのペアが10より大きい場合、その数は間違いなく素晴らしいものではありません。たとえば、 56 112、1273 79です。
これで、すべてのシーケンスのソートを開始できます。
シーケンスの合計は、2次元配列sに書き込まれます。 主対角線にはarrPrepのすべての数値が事前に入力されています。
成功したシーケンスが見つかった場合、 arrCheck検証配列にこのシーケンスの番号を入力します。
最後に、arrPrep配列とarrCheck検証配列の文字列表現を比較します。 それらが等しい場合、数字のすべての数字が少なくとも1つの成功したシーケンスで使用されます-つまり 数は素晴らしいです。
// "" function isWonderful(num) { var arrRaw=[], arrPrep=[], len=0, sum=0; // arrRaw = num.toString().split(""); for (var i=0, digit=0; i<arrRaw.length; i++){ digit=parseInt(arrRaw[i]); // if (digit>0) { arrPrep[arrPrep.length]=digit; // sum+=digit; } } // len=arrPrep.length; // 10, - "" if (sum==10) { return true; // 10 - "" } else if (sum<10) { return false; } else { // 2 2 10 - "" if ((arrPrep[0]+arrPrep[1])>10 || (arrPrep[len-1]+arrPrep[len-2])>10) { return false; } for (var i=0, s=[]; i<len; i++){ // s[i]=[]; // s[i][i]=arrPrep[i]; } // for (var i=0, arrCheck=[]; i<len-1; i++){ for (var j=i; j<len-1; j++){ // s[i][j+1]=s[i][j]+s[j+1][j+1]; // if (s[i][j+1]==10){ for (var k=i;k<=j+1;k++){ // , arrCheck[k]=s[k][k]; } break; // - } else if (s[i][j+1]>10) { break; } } } // if (arrPrep.join('')==arrCheck.join('')) { // - "" return true; } } return false; }
// "" x1, x2 function task6(x1,x2) { for (var x=x1, count=0; x<=x2; x++){ // "" - if (isWonderful(x)) { count++; } } return count; }
間隔[1、1900000]の顕著な数:152409。