ただし、仮説を検定するために使用される統計的検定の大部分(たとえば、t検定、回帰分析、分散分析)では、p値の隣に常に自由度の数などの指標があります。これは、自由度または単に省略されたdfです。今日話します

自由度、私たちは何について話しているのですか?
私の意見では、統計の自由度の概念は、適用された統計で最も重要なものであるという点で注目に値します(音声テストでp値を計算するためのdfを知る必要があります)が、同時に最も理解しにくいものの1つです統計を勉強している非数学の学生のための定義。
dfインジケータが必要な理由と、それに関する問題を理解するために、小さな統計研究の例を見てみましょう。 サンクトペテルブルクの居住者の平均成長は170センチメートルであるという仮説をテストすることにしたと仮定します。 これらの目的のために、16人のサンプルを収集し、次の結果を得ました:サンプルの平均成長は、標準偏差4で173であることが判明しました。仮説をテストするために、1平均スチューデントt検定を使用できます。標準誤差の単位での一般母集団:
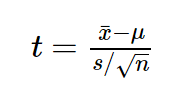
必要な計算を実行し、t基準の値が3であることがわかります。p値を計算することで問題は解決します。 ただし、t分布の特徴に精通しているため、その形状は、式n-1で計算される自由度の数に応じて変化することがわかります。ここで、nはサンプル内の観測数です。
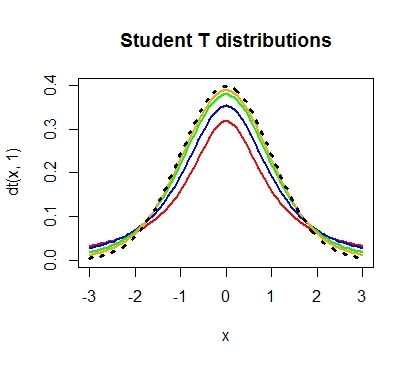
dfの計算式自体は非常にわかりやすく、観測値の数を代入して1を減算すると、答えは準備ができています。p値を計算するために残ります。この場合は0.004です。
しかし、なぜnマイナス1ですか?
統計に関する講義で私の人生で初めて、この手順に出くわしたとき、多くの学生のように、正当な質問がありました。なぜ1つを差し引くのですか? たとえば、デュースを差し引かないのはなぜですか? そして、なぜ私たちのサンプルの観測数から何かを引く必要があるのでしょうか?
教科書では、この質問に対する答えとして、将来何度も出会った次の説明を読みました。
「サンプルの平均が何であるかがわかっている場合、残りのn個の要素が何であるかを正確に判断するために、n-1個のサンプル要素のみを知る必要があります。」 それは理にかなっているように思えますが、このような説明は、t基準を計算するときになぜそれを使用する必要があるのかを説明するよりも、特定の数学的手法を説明しています。 次の一般的な説明は次のとおりです。自由度の数は、観測数と推定パラメーター数の差です。 1サンプルのt検定を使用する場合、1つのパラメーター-n個のサンプル要素を使用した一般母集団の平均値、つまりdf = n-1を推定しました。
ただし、最初の説明も2番目の説明も、観測数から推定パラメーターの数を差し引く必要がある理由を理解するのに役立ちませんか?
また、ピアソンのカイ二乗分布はどこにありますか?
答えを探してもう少し進んでみましょう。 最初にt分布の定義に目を向けると、すべての答えがそこに隠れていることは明らかです。 したがって、ランダム変数:
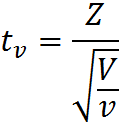
Zは標準正規分布N(0; 1)の確率変数、Vはカイ二乗分布の確率変数、νは自由度の数、確率変数ZとVは独立であるという条件で、df =νのt分布を持ちます。 これは重大な前進であり、式の分母にカイ二乗分布をもつランダム変数が自由度の数に関与していることがわかります。
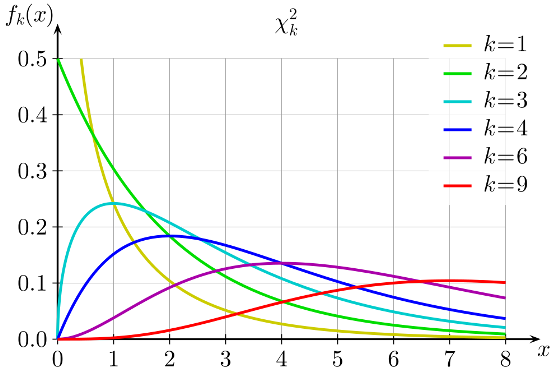
次に、カイ二乗分布の定義を調べてみましょう。 k自由度のカイ二乗分布は、k個の独立した標準正規確率変数の二乗和の分布です。
すでに目標に到達しているようです。少なくとも今では、カイ二乗分布のこのような自由度の数は、要約する正規標準分布の独立したランダム変数の数にすぎないことが確実です。 しかし、どの段階でまだ不明なままであり、なぜこの値から単位を引く必要があるのでしょうか?
この必要性を明確に示す小さな例を見てみましょう。 コイントスの結果に基づいて、重要な人生の決定を本当にしたいとしましょう。 しかし、最近、私たちはコインを食べすぎているのではないかと疑っていました。 私たちのコインが実際に正直であるという仮説を拒否しようとするために、100回のスローの結果を記録し、次の結果を得ました:ワシは60回倒れ、尾は40回倒れました。 コインが公正であるという仮説を拒否する十分な理由はありますか? これは、ピアソンのカイ二乗分布が役立つ場所です。 結局、コインが本当に正直であれば、ワシと尾の予想される理論的な頻度は同じ、つまり50と50になります。観測された頻度が予想からどれだけ逸脱しているかを簡単に計算できます。 これを行うために、ほとんどの読者に馴染みのある式に従って、ピアソンのカイ2乗距離を計算します。
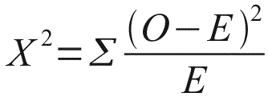
Oが観測可能な場合、Eは予想される頻度です。
事実は、帰無仮説が真である場合、実験を繰り返し繰り返すと、観測された周波数と期待された周波数の差の分布を観測された周波数の根で割ったものが正規標準分布を使用して記述でき、これはそのようなランダムな正規値の平方kの合計になります定義により、カイ二乗分布を持つ確率変数。
この論文をグラフィカルに説明しましょう。標準正規分布を持つ2つのランダムな独立変数があるとします。 次に、それらの共同分布は次のようになります。
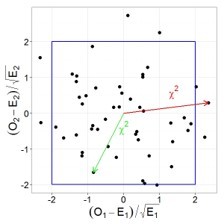
この場合、ゼロから各ポイントまでの距離の2乗は、2自由度のカイ2乗分布を持つランダム変数になります。 ピタゴラスの定理を思い出して、この距離が両方の量の値の二乗の合計であることを確認するのは簡単です。
1を引く時間です!
さて、今私たちの物語のクライマックス。 カイ二乗距離を計算する式に戻り、コインの完全性を確認し、使用可能なデータを式に代入し、ピアソンカイ二乗距離が4であることを確認します。ただし、p値を決定するには、カイ二乗分布形式の自由度を知る必要があります。それぞれこのパラメーターに依存し、クリティカル値もこのパラメーターに応じて異なります。
今から楽しい部分です。 100回のショットを何度も繰り返すことにし、ワシと尾の観測頻度を記録するたびに、必要な指標(観測頻度と予測頻度の差を予測頻度のルートで除算)を計算し、前の例のようにそれらをグラフにプロットしたと仮定します。
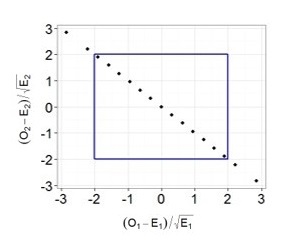
これで、すべてのポイントが1行に並んでいることがわかります。 コインの場合、私たちの条件は独立しておらず、投げの総数と尾の数を知っているため、落下したワシの数を常に正確に決定することができ、その逆も同様であるため、2つの用語が2つの独立したランダムであるとは言えません数量。 また、すべてのポイントが常に1つの直線上にあることを確認できます。30個のイーグルがいる場合は70尾、70イーグルがある場合は30尾などです。 したがって、式に2つの項があるという事実にもかかわらず、1つの自由度を持つカイ二乗分布を使用してp値を計算します。 ついに、ユニットを差し引く必要がある瞬間に到達しました。 6つの面を持つサイコロが正直であるという仮説を検証した場合、自由度5のカイ2乗分布を使用します。 結局、スローの総数と観測された5つの顔の出現頻度を知っていれば、6番目の顔のドロップ数が何に等しいかを常に正確に判断できます。
すべてが所定の位置に収まる
さて、この知識で武装し、t検定に戻ります。
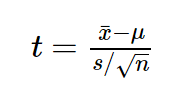
分母に標準誤差があります。これは、サンプルの標準偏差をサンプルサイズのルートで割ったものです。 標準偏差の計算には、観測値の平均値からの偏差の二乗和、つまり、複数のランダムな正の値の合計が含まれます。 そして、n個の確率変数の二乗和がカイ二乗分布を使用して記述できることをすでに知っています。 ただし、n個の項があるという事実にもかかわらず、この分布にはn-1個の自由度があります。サンプルの平均とサンプルのn-1個の要素を知っているので、常に最後の要素を正確に指定できます(したがって、平均とn個の要素を一意に識別するために必要なn-1個の要素)! t統計量の分母では、サンプル標準偏差の分布を記述するために使用されるn-1自由度のカイ2乗分布を隠していることがわかりました! したがって、t分布の自由度は、t統計式に隠れているカイ2乗分布から実際に取得されます。 ところで、調査対象の形質が一般母集団に正規分布を持っている場合(またはサンプルサイズが十分に大きい場合)、および人口の成長の平均値の仮説をテストするという目標が本当にあった場合、上記のすべての考慮事項が真であることに注意することが重要ですノンパラメトリック基準を使用する方が合理的です。
自由度の数を計算するための同様のロジックは、他のテスト、たとえば回帰分析または分散分析で作業する場合に保持されます。これは、関連する基準を計算する式に存在するカイ二乗分布のランダム変数にあります。
したがって、統計的研究の結果を正しく解釈し、単一サンプリングt検定などの単純な基準を使用した場合に得られるすべての指標がどこで発生するかを理解するために、研究者は数学的なアイデアが統計的方法の根底にあるものをよく理解する必要があります。
オンライン統計コース:複雑なトピックを簡単な言語で説明する
バイオインフォマティクス研究所で統計を教える経験に基づいて、データ分析に専念する一連のオンラインコースを作成するというアイデアがありました。そこでは、最も重要なトピックがそれぞれにアクセス可能な形式で説明され、さまざまな問題を解決するために統計的手法を自信を持って使用するために理解が必要です 2015年に、これまでに約1万7千人が登録した「統計の基礎」コースを開始し、3千人の学生がすでに修了証明書を取得しており、コース自体がEdCrunch Awardsを受賞し、最高の技術コースとして認められています。 今年、 stepik.orgプラットフォームで、 統計の基礎コースの継続が開始されました。 第2部では、統計の基本的な方法に精通し、最も複雑な理論的問題を分析します。 ところで、このコースの主要なトピックの1つは、統計的仮説のテストにおけるピアソンのカイ2乗分布の役割です。 そのため、観測の総数から単位を減算する理由についてまだ質問がある場合は、コースでお待ちしています!
また、統計分野の理論的知識は、学術目的で統計を使用する人だけでなく、応用分野でデータ分析を使用する人にも間違いなく役立つことは注目に値します。 統計の基本的な知識は、機械学習とデータマイニングの分野で使用されるより複雑な方法とアプローチを習得するために必要です。 したがって、統計学の導入コースを正常に完了することは、データ分析の分野での良いスタートです。 データスキルの獲得について真剣に考えているのであれば、オンラインデータ分析プログラムに興味があるかもしれません。これについては、 ここで詳しく説明しました 。 上記の統計コースはこのプログラムの一部であり、統計と機械学習の世界にスムーズに浸ることができます。 ただし、データ分析プログラムのコンテキスト外であっても、誰もが期限なくこれらのコースを受講できます。