 ハブラハブル、親愛なる同僚! ハニカムを見るとき、私はミツバチについてではなく、シュレフリのシンボルについて考えます。 この記事を読んだ後は、古い方法で世界を見ることができなくなります。ハニカムと通常の多面体の間には直接的なつながりがあることがわかります。
ハブラハブル、親愛なる同僚! ハニカムを見るとき、私はミツバチについてではなく、シュレフリのシンボルについて考えます。 この記事を読んだ後は、古い方法で世界を見ることができなくなります。ハニカムと通常の多面体の間には直接的なつながりがあることがわかります。
4次元空間と高次元の空間で正しい多面体の結論を友人に説明した経験から、シュレフリ記号が何であるかを知っている人はほとんどいないことがわかったので、他の隣接する記事で行った分析計算なしに、別の記事を写真でそれに捧げることにしました、多面体を直接導出します。 この記事では、私の仕事はシュレフリ記号という用語を比intuitive的に直感的に理解することです。したがって、ウィキペディアで読むことができる厳密な定義と定式化に注意を払うつもりはありません。 Shlefly Symbolのコンセプトは、簡単なものから難しいものまでマスターされます。 飛行機の中で最もシンプル。
三角形はどのように配置されていますか? 回答:3つの同一の側面から。 シュレフライのシンボル{3}
正方形はどのように配置されていますか? 回答:4つの同一の側面から。 シュレフライのシンボル{4}
正六角形はどのように配置されますか? 回答:9つの同一の側面から。 Shleflyシンボル{9}写真を参照:

本当の初歩的な質問? 反対方向に進みましょう-Shlefly Symbol {10}で定義された正多角形の名前と構造は何ですか?
答え
通常の十角形で、10個の同一の側面で構成されています。
したがって、最も単純なものはすべて、2次元空間のShleflyシンボルです。 表記{p1}。ここで、p1は3以上の整数です。単純な意味で、双角形がないためです。 この場合の数値p1は、正多角形(2次元多面体)のエッジの数を示しています。上の図を参照してください。
{3}は正三角形、{4}は正方形、{9}は正八角形などです。
平面上-これはシュレフリ記号を理解するための最初のステップです。記号と多角形の構造との関係が明確であることを願っています。 3次元の正多面体の場合、これらの多面体の構造に関する質問への答えもシュレフリ記号を与えます。 つまり Schlefliシンボルは、正多角形の辺の数の概念を正多角形に一般化します。
つまり、キューブはどのように配置されますか?
答え 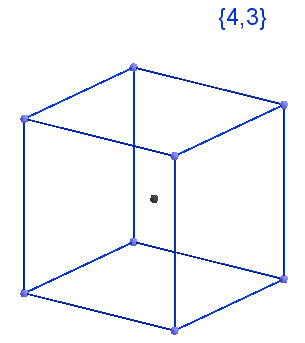 キューブは{4、3}で、これはそのシュレフリ記号です。つまり、4つの四角形で構成され、上部が3つの部分に収束します。 左の図。
キューブは{4、3}で、これはそのシュレフリ記号です。つまり、4つの四角形で構成され、上部が3つの部分に収束します。 左の図。
つまり 立方体は、各頂点で3つの正方形{4}を接続することによって取得されます。 頂点の1つでの接着がビデオに示されています。
 キューブは{4、3}で、これはそのシュレフリ記号です。つまり、4つの四角形で構成され、上部が3つの部分に収束します。 左の図。
キューブは{4、3}で、これはそのシュレフリ記号です。つまり、4つの四角形で構成され、上部が3つの部分に収束します。 左の図。
つまり 立方体は、各頂点で3つの正方形{4}を接続することによって取得されます。 頂点の1つでの接着がビデオに示されています。
プログラムリンク
アニメーションが描画される無料のプログラムはGeoGebraと呼ばれ、こちらからダウンロードできます: www.geogebra.org/download
このビデオはUbuntuオペレーティングシステムで記録されたもので、記録プログラムはrecordmydesktopと呼ばれます。
このビデオはUbuntuオペレーティングシステムで記録されたもので、記録プログラムはrecordmydesktopと呼ばれます。
同様に、残りの4つの正多面体は、シュレフリ記号によって定義されます。
八面体はどのように配置されていますか?
答え 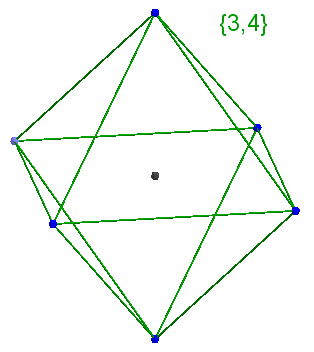 {3、4}-シュレフリ記号。これは、八面体が上部の4つの部分に収束する3つのゴンで構成されていることを意味します。
{3、4}-シュレフリ記号。これは、八面体が上部の4つの部分に収束する3つのゴンで構成されていることを意味します。
 {3、4}-シュレフリ記号。これは、八面体が上部の4つの部分に収束する3つのゴンで構成されていることを意味します。
{3、4}-シュレフリ記号。これは、八面体が上部の4つの部分に収束する3つのゴンで構成されていることを意味します。 二十面体はどのように配置されていますか?
答え 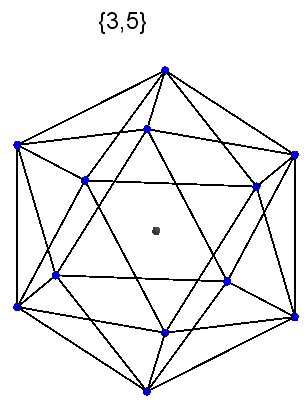 {3、5}-シュレフリ記号。これは、正二十面体が、上部で5つの部分に収束する3つのゴンで構成されていることを意味します。
{3、5}-シュレフリ記号。これは、正二十面体が、上部で5つの部分に収束する3つのゴンで構成されていることを意味します。
 {3、5}-シュレフリ記号。これは、正二十面体が、上部で5つの部分に収束する3つのゴンで構成されていることを意味します。
{3、5}-シュレフリ記号。これは、正二十面体が、上部で5つの部分に収束する3つのゴンで構成されていることを意味します。 戻りましょう、シュレフライシンボルはどのような形を意味しますか?
答え  四面体
四面体
 四面体
四面体 Shlefliシンボルの意味は、{5、3}、上部の3つの五角形を意味しますか?
答え 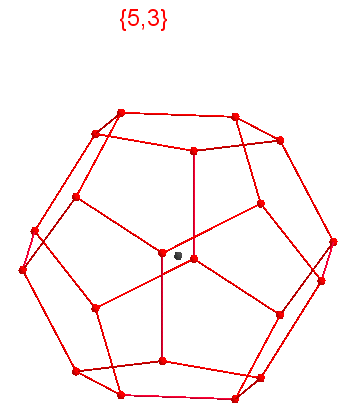 十二面体
十二面体
 十二面体
十二面体 これは、正多面体の3次元シュレフリ記号の全体的な意味です。 3次元では、適切な多面体を感じることができ、写真やビデオではっきりと示すことができるので、通常の3次元性は、シュレフリシンボルの本質を明確に理解できる最良の空間です。 そして、この線が克服されると、私たちは深まり、それを難しくします。
当初、3Dプリンターで正しい多面体を印刷したいという強い願望があったので、Habréの1つの記事の推奨で無料のOpenSCADプログラムを学び始めました 。
同時に、Shlefli Symbolを使用して(つまり、2つの入力パラメーターp1、p2を使用して)対応する正多面体を構築するアルゴリズムを予期せずに記述しました。 このような統一されたアルゴリズムを作成できたことは素晴らしいことです。これは独立した小さく興味深い結果です。一方、リストは1つの画面に収まりますが、ifステートメントは1つだけであり、最も重要なのは、Shleflyシンボルの意味を非常に明確に実証できることです。 このアルゴリズムは、3次元の正多面体の構造が2つのパラメーター{p1、p2}のみに依存することを示すことができました。以下のビデオを参照してください。 ビデオを見るときは、タスクを完了する必要があります。多面体の2次元の面にいくつのエッジがあり、上部に収束する2次元の面の数を計算する必要があります。 このタスクを完了すると、Schlaflyシンボルの謎が永遠に明らかになります。
コメント付きのアルゴリズムソース
// {p1, p2} /* {3,3} - {3,4} - {4,3} - {3,5} - {5,3} - */ p1=5; // p2=3; // // accuracy=100; // sphere_radius = 10; // edge_angle_half = 90-asin(cos(180/p1)/sin(180/p2)); // edge_length_half = sphere_radius*sin(edge_angle_half); // rb_face = edge_length_half/sin(180/p1); // rs_face = edge_length_half/tan(180/p1); // angle_up = 180-2*asin(cos(180/p2)/sin(180/p1)); // angle_up1 = asin(sin(90-asin(cos(180/p1)/sin(180/p2)))/sin(180/p1)); // rs_polytop=sphere_radius*cos(angle_up1); // ch=rs_polytop; //ch=1; // //difference() { rotate([0, angle_up1, 0]){// , , 3D union(){ ten_edge();// if (!(p1==3 && p2==3)) rotate([0, 180, 0]) ten_edge();// , , , } } //sphere(r=rs_polytop-0.3, $fn=accuracy);// , 3D //} module ten_edge(){ translate([0, 0, -sphere_radius]) for (i=[0:1:p2]) rotate([0, -angle_up1, i*360/p2])/* , p2 Oz, 1, */ translate([rb_face, 0, 0])/* , */ rotate([0, 0, (180/p1)*(1-p1+2*floor(p1/2))])/* */{ union(){ rotate([0, 0, 180/p1]) cylinder(h=ch, r1=rb_face, /*r2=rb_face-0.75*/ r2=0, center=false, $fn=p1);// , , translate([rs_face, 0, 0]) rotate([0, -angle_up, 0]) translate([rs_face, 0, 0]) rotate([0, 0, 180+180/p1]) cylinder(h=ch, r1=rb_face, /*r2=rb_face-0.75*/ r2=0, center=false, $fn=p1);// } } }
OpenSCADをダウンロードしてそこにアルゴリズムソースを挿入し、多面体を自分で実験することをお勧めします。 最も好奇心The盛な人はそこに他の数字を挿入したいと思うでしょう。 三次元には通常の多面体が5つしかないことを忘れてしまったので、ビデオではすべての可能なオプションを示しています。三次元には他にはありません。
次のステップは、Shlefly Symbols {4、4}、{6、3}、{3、6}が何を意味するのか答えることです。
ヒント:これらは多面体ではなく、誰もが視覚的に知っている他の数字です。
回答:{4、4}
{4、4}-これはセル内の紙切れで、四角形が上部に4つの部分に収束します。 実際、セルは正方形であり、すべての正方形の頂点でこれらの正方形の4つが収束します。 これは、ユークリッド平面の正方形への分割であり、無期限に継続できます。
{6、3}とは何ですか?
答え 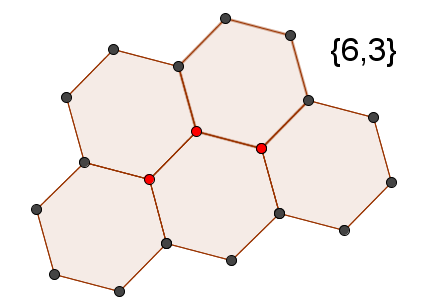 ハニカム
ハニカム
 ハニカム
ハニカム そして、{3、6}とは何ですか?
答え 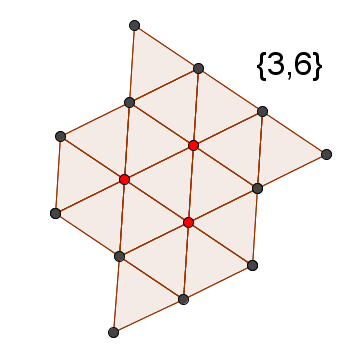 ポイントは赤で強調表示され、6つの収束する三角形がすべて表示され、残りの頂点では描画を続ける必要がありますが、無限に続けることができるので、何かで停止する必要がありました。
ポイントは赤で強調表示され、6つの収束する三角形がすべて表示され、残りの頂点では描画を続ける必要がありますが、無限に続けることができるので、何かで停止する必要がありました。
 ポイントは赤で強調表示され、6つの収束する三角形がすべて表示され、残りの頂点では描画を続ける必要がありますが、無限に続けることができるので、何かで停止する必要がありました。
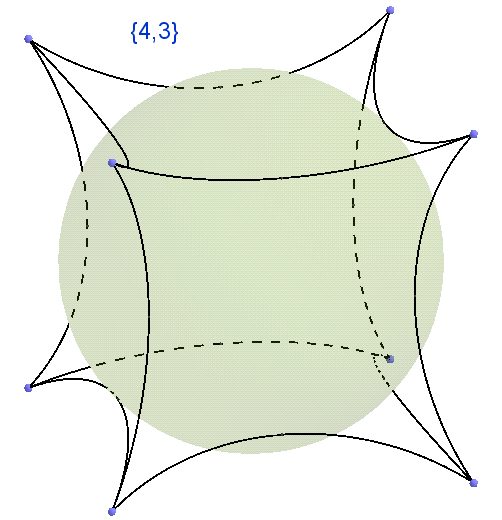
ポイントは赤で強調表示され、6つの収束する三角形がすべて表示され、残りの頂点では描画を続ける必要がありますが、無限に続けることができるので、何かで停止する必要がありました。 さて、ユークリッド平面の既存の3つのパーティションすべて(バトルという言葉に重点を置いて)を調べました。他にはありません。これは記事で示しました。セルにノートブックを置くと、これらは単純なセルではなく、ユークリッド平面のパーティション{4,4}です; ハニカムを見ると、{6,3}であることを思い出してください。 {3,3}も目を引くと思います。 それぞれが独自のシュレフリ記号で示されている多面体から、シュレフリ記号でも示されているユークリッド平面のパーティションに切り替えました。 シュレフリ記号を理解することの難しさの次のステップ(一般化)は、それが球体の区分を定義することです。 したがって、{3、4}は一方では正八面体であり、他方では球体を規則的な球状の三角形に分割し、上部で4つのピースを収束させます。 {4、3}-一方は立方体、他方は球体を規則的な球体の四角形に分割し、頂点で3個に収束します。 これはビデオでより明確に示されています。 2次元の面の数と、そのような面が頂点で収束する数を数えます。
オブジェクトのクラス全体のうち、ビデオに示されているエッジを曲げる場合、2つが最も興味深いものです。
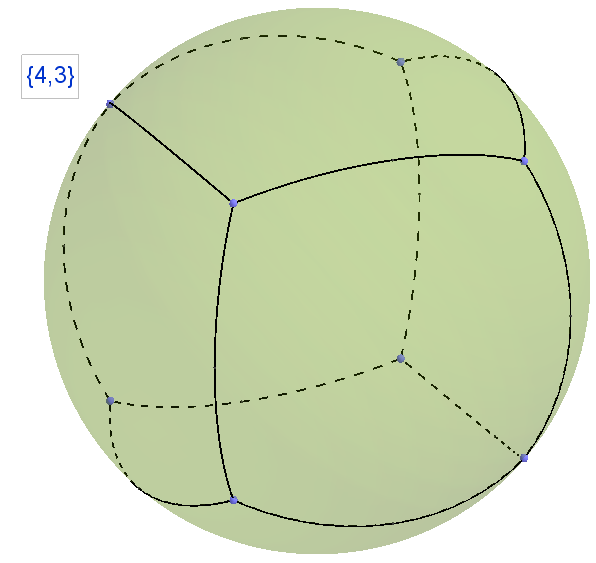
図 33 2次元の球体を正方形に分割し、各頂点に3つのピース、シンボル{4.3}
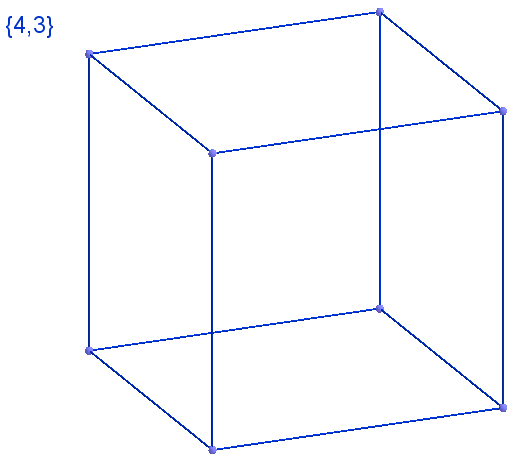
図 34正しい多面体、立方体、記号も{4,3}
八面体のエッジの曲げに関する次のビデオ、{3,4}
オブジェクトのクラス全体のうち、ビデオに示されているエッジを曲げる場合、2つも最も興味深いものです。
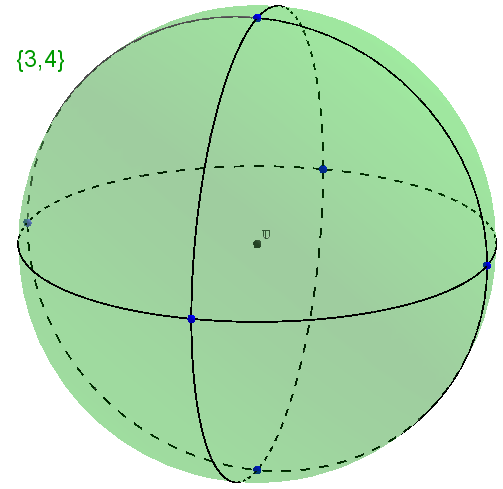
図 35 2次元の球体を三角形に分割し、各頂点に4つのピース、シンボル{3,4}

図 36正多面体、八面体、記号も{3、4}
多面体を少し膨らませます(球体に置きます)が、平坦な面も膨らみ、頂点の角度と二面角は端で増加します。 または、それを吹き飛ばし(ロバチェフスキー空間に配置)、平らな面も収縮し、頂点の角度とエッジの二面角が減少します。
つまり シュレフリのシンボルは、図の全体のクラスを定義します。 切れ目のないエッジの曲がりはシュレフリ記号を変更しません。これは、リブが曲がり、シュレフリ記号が同じままである間、シュレフリ記号指定が記録全体を通して表示されるという事実によってビデオに示されています。 ビデオは、フィギュアのすべてのコーナーが同時に均等に変化する特別な曲げを示しています。
Shlefly Symbolによって定義された図のクラス全体のうち、主に3つの特定のケースに関心があります。
-シュレフリ記号が正多面体を定義する場合。
-シュレフリ記号が球体のパーティションを定義する場合。
-シュレフリ記号がロバチェフスキー空間のパーティションを定義する場合。
これらのケースと関連するケースは、上のビデオに示されています。 ビデオには立方体と八面体のみが表示されていますが、状況は{3,3}-四面体、{3,5}-正二十面体、{5,3}-十二面体の他の3つの正多面体とまったく同じです。 この瞬間から、私たちが球体のパーティションについて話し始めたとき、私たちは作業する空間の次元に非常に注意しなければなりません。 実際、球体の表面は2次元で、多面体は3次元ですが、球体のパーティションと対応する多面体は同じシュレフリ記号で示されます。 たとえば、すでに述べたように、{3、4}は3次元ユークリッド空間の八面体であり、{3、4}は球体の2次元表面を球面三角形に分割したものです。 二次元球面空間のパーティション。 球面三角形とは直感的なものですが、この問題を明確にしたい人は誰でも記事で見つけることができます。 したがって、球体の表面のパーティションを定義するシュレフリ記号について話すとき、同時に空間の2つの隣接する次元にいます。 同時に、Schleafly Symbol {3、6}はユークリッド平面のパーティションを定義します。つまり、 ユークリッド平面のパーティションも近くにあります。
さて、次の難易度(一般化)に進み、ロバチェフスキー平面のバトルについて話し始めると、絵の完全性とシュレフライシンボルの意味の理解が生じます。 心配しないでください。ロバチェフスキー平面で作業するのに十分な基本的で直観的なスキルがあります。そのようなスキルは球体と同じ記事で与えられ、ロバチェフスキー平面のこれらのパーティションの写真もそこに与えられます。 これは極端な悪化のステップではありませんが、球面、ユークリッド、ロバチェフスキーの空間はすべて曲率が一定の3つの空間であるため、完全性が得られます。 したがって、シュレフリ記号{3、6}はユークリッド平面のパーティションを定義し、{3、7}はロバチェフスキー平面のパーティションを定義します。 {3、8}、{3、9}など {3、p2}ここで、p2> = 7はすべて、ロバチェフスキー平面の正三角形への分割です。 このようなパーティションの数は無限です(可算数)。 例として、パーティション{3,7}と{5,4}の2つの画像を提供します。最初のケースでは7つの三角形が各頂点で収束し、2番目では4つの五角形であることを確認します。
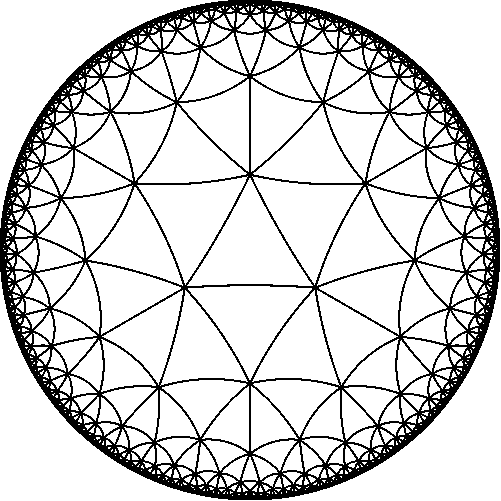
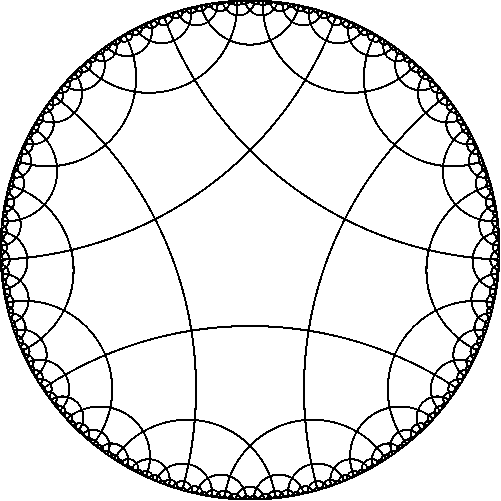
球体空間とロバチェフスキー空間を操作するには、オブジェクトが球体に配置されると「膨張」し、ロバチェフスキー空間に配置されると「収縮」すると想像するだけで十分です。
シュレフリ記号を理解する(理解する)次のステップは、シュレフリ記号によると、3次元球面空間のパーティションに接続されている4次元ユークリッド空間に移動することです。 -立方体と球体の球形の正方形への分割。 ここで絵を描いたり、想像力を働かせたりするのはもっと難しいですが、何かを描いてみます。
最初に理解すべきことは、Shlefly Symbol {p1、p2}からShlefly Symbolへの遷移で、{p1、p2、p3}より1次元高いものです。 {4.3}から{4.3.4}への移行を示します。 したがって、3次元の{4、3}四辺形(平面)では、それらはエッジ(1次元の面)に沿って接着され、頂点で3個に収束します(頂点は0次元の面です)。 同様に、Schleufly Symbol {p1、p2、p3}の場合、たとえば{4、3、4}-これは{{4、3}、4}と同じです。つまり、キューブは{4,3}(3次元の面)です。 、正方形(2次元の面)で接着され、rib骨(1次元の面)に収束します。各辺に4個あります。 それでは、{4、3、4}とは何ですか? 各リブに4つの立方体が集まりましたが、それは何ですか? 答えを開く前に考えてください。
答え  これは、3次元ユークリッド空間の立方体への分割です。 簡単です。これはよく知られたオブジェクトです。 正確に4つの立方体がエッジに集まっていることに注意してください。これは、エッジが赤で強調表示されている例で示されています。 シンボル{p1、p2、p3} = {4、3、4}の数字p3は、p3 = 4個の多面体がエッジに収束することを意味し、数字{p1、p2}の意味は同じままです。リブ。
これは、3次元ユークリッド空間の立方体への分割です。 簡単です。これはよく知られたオブジェクトです。 正確に4つの立方体がエッジに集まっていることに注意してください。これは、エッジが赤で強調表示されている例で示されています。 シンボル{p1、p2、p3} = {4、3、4}の数字p3は、p3 = 4個の多面体がエッジに収束することを意味し、数字{p1、p2}の意味は同じままです。リブ。
 これは、3次元ユークリッド空間の立方体への分割です。 簡単です。これはよく知られたオブジェクトです。 正確に4つの立方体がエッジに集まっていることに注意してください。これは、エッジが赤で強調表示されている例で示されています。 シンボル{p1、p2、p3} = {4、3、4}の数字p3は、p3 = 4個の多面体がエッジに収束することを意味し、数字{p1、p2}の意味は同じままです。リブ。
これは、3次元ユークリッド空間の立方体への分割です。 簡単です。これはよく知られたオブジェクトです。 正確に4つの立方体がエッジに集まっていることに注意してください。これは、エッジが赤で強調表示されている例で示されています。 シンボル{p1、p2、p3} = {4、3、4}の数字p3は、p3 = 4個の多面体がエッジに収束することを意味し、数字{p1、p2}の意味は同じままです。リブ。 したがって、次のステップは、シンボル{4、3、3}の意味を考慮することです。 3次元ユークリッド空間のキューブ{4,3,4}への分割がありましたが、エッジからキューブを1つ投げてみましょう。{4,3,3}が得られます。ユークリッドでは何ですか?
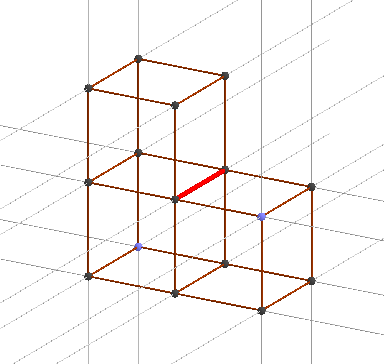 キューブの平らな面が接着されていないため、これがパーティションではないことは明らかではないことが判明しました。 彼らが一緒に固執するために何をする必要がありますか? これらの立方体をボールのように膨らませ、立方体の2次元の面が一致するまで膨らませる必要があります。ここでそれらを接着します。 Inflateは比expression的な表現です。数学では、球体に立方体を配置する(3次元である)と呼ばれ、2次元の球体で球形の三角形を考える方法と同様に、立方体を球体にしますが、今では立方体が3次元であるため、立方体を3次元の球体に配置します。 球自体は4次元のユークリッド空間に配置されますが、その表面は3次元です。 つまり {4,3,3}は3次元の球体を立方体に分割し、3つの部分をエッジに収束させます。
キューブの平らな面が接着されていないため、これがパーティションではないことは明らかではないことが判明しました。 彼らが一緒に固執するために何をする必要がありますか? これらの立方体をボールのように膨らませ、立方体の2次元の面が一致するまで膨らませる必要があります。ここでそれらを接着します。 Inflateは比expression的な表現です。数学では、球体に立方体を配置する(3次元である)と呼ばれ、2次元の球体で球形の三角形を考える方法と同様に、立方体を球体にしますが、今では立方体が3次元であるため、立方体を3次元の球体に配置します。 球自体は4次元のユークリッド空間に配置されますが、その表面は3次元です。 つまり {4,3,3}は3次元の球体を立方体に分割し、3つの部分をエッジに収束させます。 
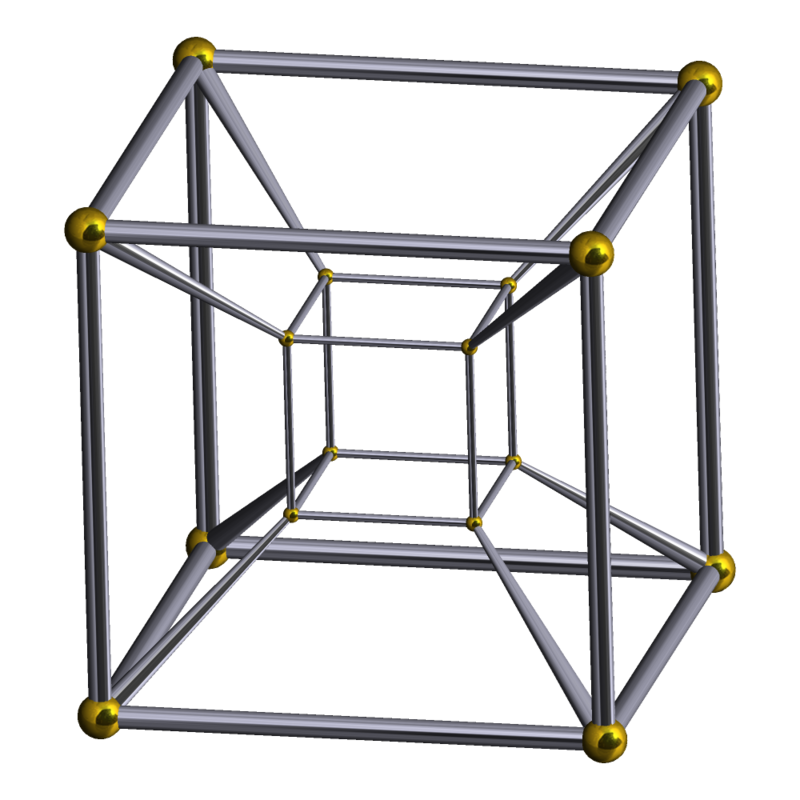 平面上に4次元を描くことは困難ですが、人々はすでにこれを行う方法を学んでおり、エッジの曲がり方(左)に注意してください。これは、球上のオブジェクト{4,3,3}、この場合は3次元球のパーティションを意味するためです しかし、球体のパーティションは球体の表面より1次元高い多面体に対応することが既にわかっているため、{4,3,3}は4次元ユークリッド空間の正多面体(右側)で、これはTesseract、4次元立方体です。 ほぼ同じことですが、3次元の多面体でエッジを曲げるのと同様に、直線のエッジのみがスチールになりました。また、目的の結果が得られるまで、4次元の多面体でエッジを曲げることができます。
平面上に4次元を描くことは困難ですが、人々はすでにこれを行う方法を学んでおり、エッジの曲がり方(左)に注意してください。これは、球上のオブジェクト{4,3,3}、この場合は3次元球のパーティションを意味するためです しかし、球体のパーティションは球体の表面より1次元高い多面体に対応することが既にわかっているため、{4,3,3}は4次元ユークリッド空間の正多面体(右側)で、これはTesseract、4次元立方体です。 ほぼ同じことですが、3次元の多面体でエッジを曲げるのと同様に、直線のエッジのみがスチールになりました。また、目的の結果が得られるまで、4次元の多面体でエッジを曲げることができます。

エッジ{4,3,4}で4を収束する立方体への3次元ユークリッド空間のよく知られたパーティションに戻りましょう。 上記では、1つの立方体を{4,3,3}に投げ、立方体の平らな面が一致するまで残りの3つの立方体を膨らませました。 しかし、既存の4つの立方体を吹き飛ばし、2つの隣接する立方体を平らな面に沿って1か所で分離し始めたらどうでしょうか? そうすると、これらの面の間に隙間ができます。 しかし、別の同様の「収縮した」立方体がこのギャップに収まるまでさらに吹き飛ばすと、{4,3,5}-3次元ロバチェフスキー空間の立方体への分割が得られます。 厳密に言えば、キューブを吹き飛ばしたときに、ロバチェフスキー空間に配置しました。
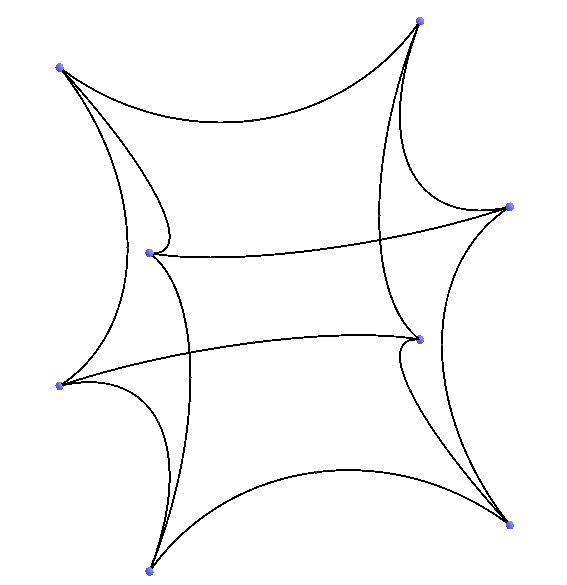
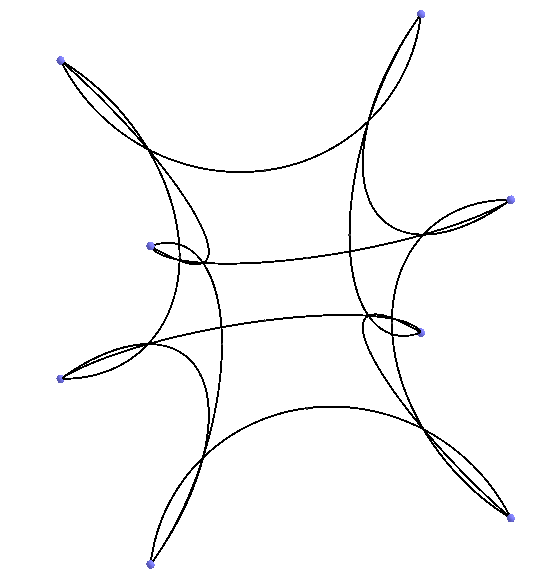 ビデオの1つで、上記の収縮したキューブを既に見ました(左の写真)。 したがって、吹き飛ばすことによって、3次元のロバチェフスキー空間のパーティションを通常の多面体にします。 注意する必要があります。キューブを長時間吹き飛ばすことはできません。さもないと、エッジの自己交差が形成されます(右図)。 図では自己交差を形成していますが、3次元ロバチェフスキー空間の意味では、これは立方体の頂点が絶対を超えていることを意味します。 したがって、エッジあたり6個の立方体は、シュレフリ記号{4,3,6}で示され、すでに3次元ロバチェフスキー空間のこのパーティションでは、頂点は絶対座標上に直接配置されています。 {4,3,7}では、頂点はすでに絶対を超えています。これらのシュレフリーシンボルは、3次元のロバチェフスキー空間のパーティションも示していますが、厳密に言えば、通常の多面体ではなく他の何かに、ここでこれらのオブジェクトを何と呼び、同意するかをすでに理解できます彼らの名前について。
ビデオの1つで、上記の収縮したキューブを既に見ました(左の写真)。 したがって、吹き飛ばすことによって、3次元のロバチェフスキー空間のパーティションを通常の多面体にします。 注意する必要があります。キューブを長時間吹き飛ばすことはできません。さもないと、エッジの自己交差が形成されます(右図)。 図では自己交差を形成していますが、3次元ロバチェフスキー空間の意味では、これは立方体の頂点が絶対を超えていることを意味します。 したがって、エッジあたり6個の立方体は、シュレフリ記号{4,3,6}で示され、すでに3次元ロバチェフスキー空間のこのパーティションでは、頂点は絶対座標上に直接配置されています。 {4,3,7}では、頂点はすでに絶対を超えています。これらのシュレフリーシンボルは、3次元のロバチェフスキー空間のパーティションも示していますが、厳密に言えば、通常の多面体ではなく他の何かに、ここでこれらのオブジェクトを何と呼び、同意するかをすでに理解できます彼らの名前について。
同様に、他の3次元の正多面体からパーティションを取得します。
{3,3}-四面体、エッジで3つの四面体を結合{3,3,3}、ギャップがあり、面が接着されるまでそれらを膨らませます。3次元球体を四面体に分割し、エッジで3つの部分に収束します。 このパーティションは、4次元ユークリッド空間{3,3,3}の正多面体を定義します。
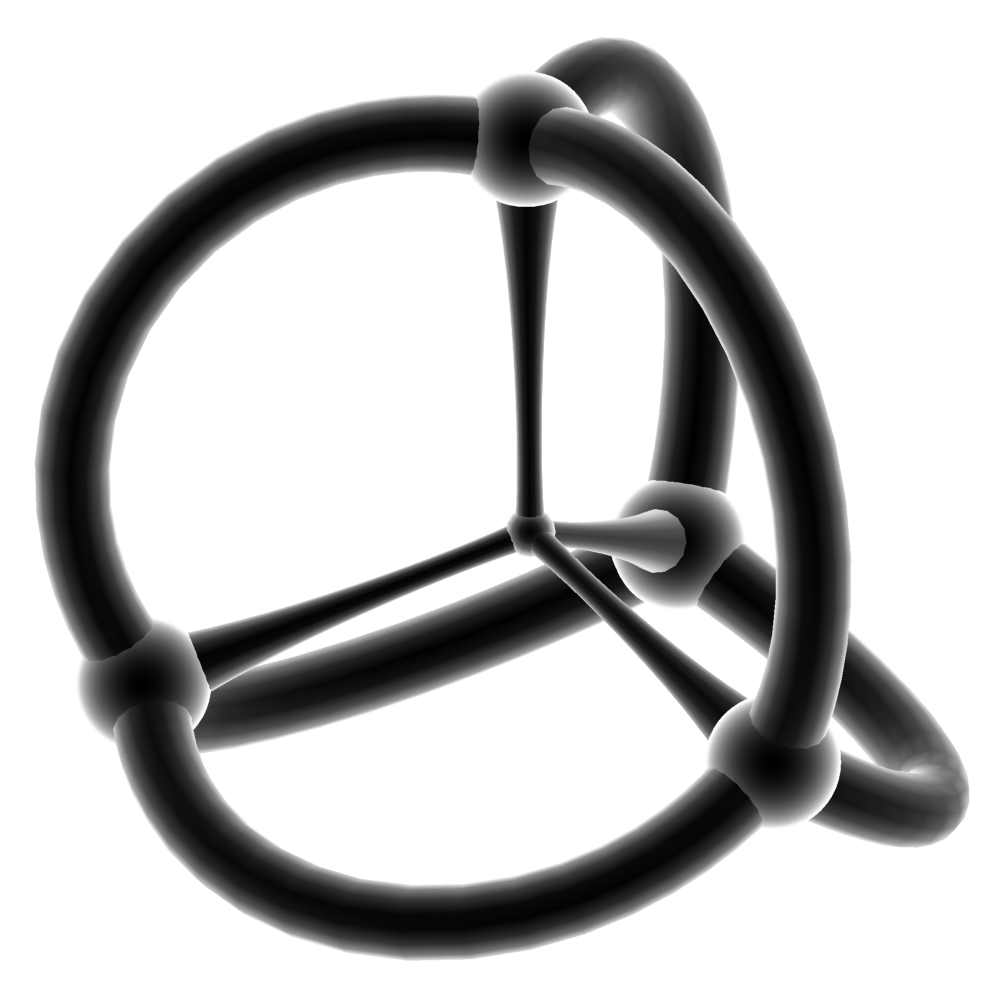
図22 3次元球体のパーティション{3,3,3}。

図23 4次元多面体{3,3,3}
3次元球と多面体の残りのパーティションについては、同様です。

図24 3次元球{3,3,4}のパーティション。

図25 4次元多面体{3,3,4}

図26 3次元球{3,3,5}のパーティション。

図27 4次元多面体{3,3,5}

図28 3次元球体のパーティション{3,4,3}。
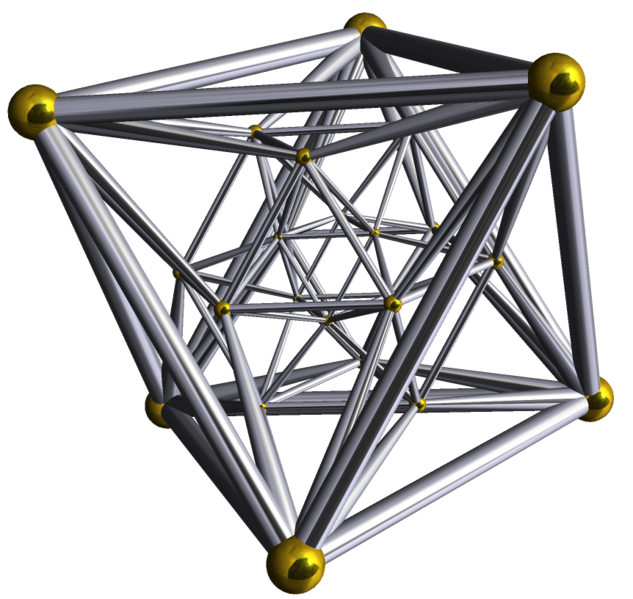
図29 4次元多面体{3,4,3}
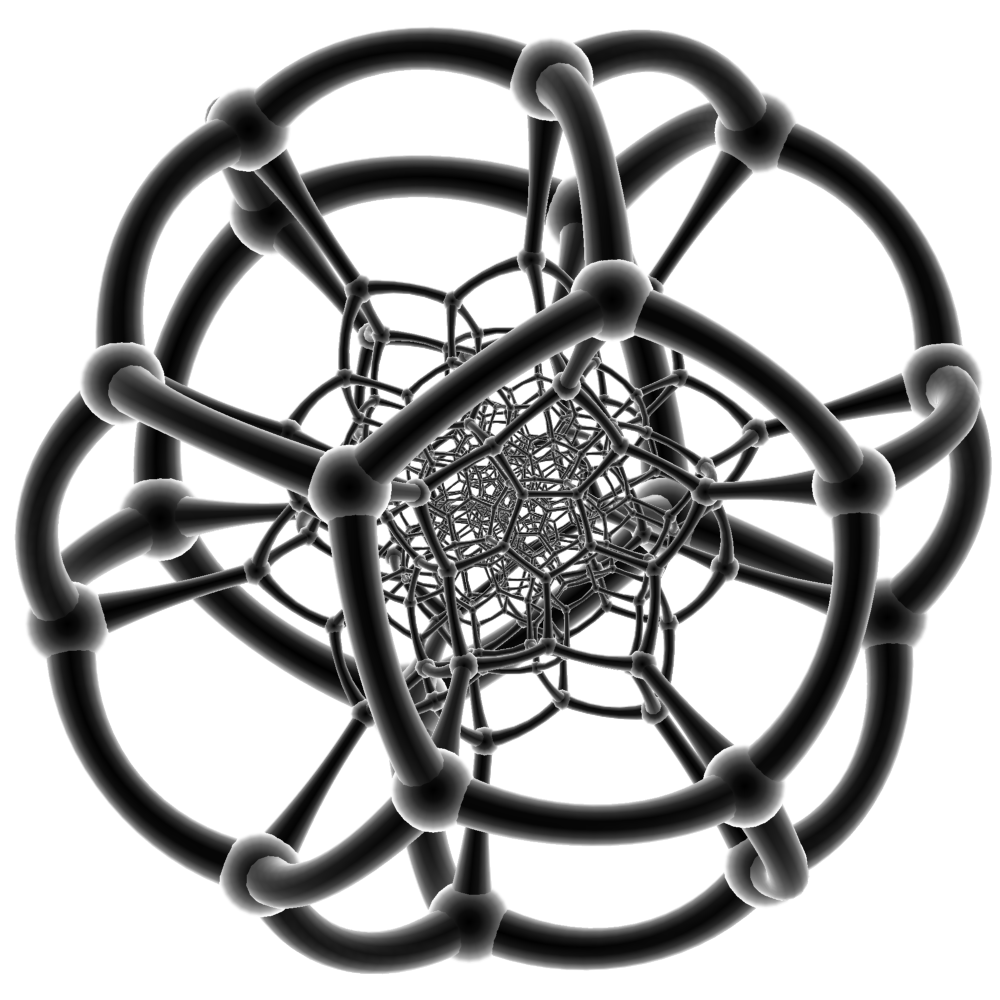
図30 3次元球体のパーティション{5,3,3}。

図31 4次元多面体{5,3,3}
3次元のロバチェフスキー空間のパーティションでも、すべてが似ています。頂点が絶対に飛び出さないように、多面体を吹き飛ばすだけで、忘れないでください。 シュレフリ記号による頂点の位置を決定するのは非常に簡単です。{p1、p2、p3}の場合、{p2、p3}がユークリッド平面を分割する場合、記号{p2、p3}を考慮します。 値{4,4}、{3,6}、{6,3}のいずれかを取る場合、これは頂点{p1、p2、p3}が絶対値上にあることの確実な兆候です。たとえば、{3,3,6}、{ 3,4,4}、{3,6,3}など。 {p2、p3}-ロバチェフスキー平面を分割する場合、頂点{p1、p2、p3}は絶対の背後にあります。たとえば、これらは{3,3,7}、{3,4,5}、{3,6,4}などです。 。 {p2、p3}-球体を分割するが、{p1、p2、p3}-球体を破壊しない場合、{p1、p2、p3}-3次元ロバチェフスキー空間を分割する場合、これらのオプションをすべてリストします:{4 、3、5}、{3、5、3}、{5、3、4}、{5、3、5}そのような他のものはありません。
空間の他の次元の多面体とパーティションの場合、物事は完全に類似しています。 高次元の空間のシュレフリ記号は、{p1、p2、p3、p4、... pn}と記述されます。
バルーンを膨張および収縮させることを学べば、一定の曲率の空間に問題はありません。
そして結論として、多面体の双対性の性質についてのいくつかの言葉。 Shlefliシンボルが逆の順序で記述されている場合、正しい多面体も取得します。これは元の多面体のみです。 したがって、八面体と立方体は互いに二重です。 {3,4}-{4,3}。 四面体は自己双対の{3,3}-{3,3}です。 二十面体と十二面体は二重で、{3,5}-{5,3}です。 これは、エッジのサイズと正多面体の角度を計算するのに役立つ非常に重要なプロパティです。 この記事で使用したすべての図面を作成するとき、このプロパティを非常に積極的に使用しました。 また、十二面体を構築するとき、立方体が十二面体の内側にはっきりと収まるという性質が非常に重要であることが判明し、立方体の頂点が直接十二面体の頂点に落ちます。 これは、十二面体の8つの頂点の座標を見つけるのに役立ちました;十二面体の残りの頂点は見つけるのが難しくありませんでした。 ここでは、それらは多面体であり、互いに非常に似ています。 双対性とは、1つの多面体の頂点が、2番目の多面体の平面の中心に最初の双対面と接することを意味します。 3次元多面体の例では、これらのすべてのプロパティがビデオに示されています。
ソースをダウンロードして、多面体を自分で試すことができます:それらをねじって、rib骨を曲げて、二重性を見てください。
双対性プロパティは、スペースの他のすべての次元で保持されるため、{3,3,5}は双対{5,3,3}などです。
この記事は、すべての次元での正多面体の導出に関する一連の記事の一部として作成されました。
多面体を修正します。 パート1.三次元
多面体を修正します。 パート2. 4次元
多面体を修正します。 パート2.5(補助)
Shleflyのシンボル。 パート2.6
これらの記事の最終的な目標は、次元3以上ですべての規則的な凸多面体の導出を示すことです。 パート2の発行後、私はその資料があまり受け入れられないと感じ、長い間その理由を考え、人々は単純にシュレフリ記号のようなシンプルで強力なツールに精通していないという結論に達しました。そこで、この記事を書きました。 次の記事は第3部で、空間の次元で誘導遷移を行い、多面体と多面体自体の二面角の最終式を取得する必要があります。
ご清聴ありがとうございました。 タッチで。 またね