
私はHabrのサイトが好きです。私は特に人々が自分の「技術的」思考を紙の上で正しく表現する方法が好きです。 そのため、コメントですべてを可能な限り説明しようとしました-私にとっては非常に簡単であり、あなたがそれを理解する方が便利です。
コードはMATLABで記述されています。 特定のスペルでは、構文は簡単に理解できます。 アルゴリズムを書くとき、コードの「理解」と実行速度のバランスを維持し、ベクトル化を排除し、どこにあるかを試しました-代替コードがコメントに書かれていました。 質問がある場合-私はコメントで答えようとします。 これは「例による最適化」シリーズの最初の部分であり、コメントに応じてさらに出版物がリリースされます。 つまり、他のヒューリスティック手法との比較が必要な場合、または提案(温度式やアリの初期位置の変更など)がある場合、それを調整できる場所、およびアルゴリズムの一部を変更する場所-書き込み。 それは皆、そして私にとっても興味深いものになるでしょう。 可能であれば、実装して公開します。
この出版物の目的は、まず、コード内の詳細なコメントに2つのアルゴリズムの原理を示すことであり、比較は二次的な目標です。 この記事では、2つのアルゴリズム、特にantには適切な数の初期変数パラメーターが含まれているため、「純粋に」比較することはできません。 さらに、いくつかの疑問が生じましたが、それについては後で詳しく説明します。 シミュレーテッドアニーリングでは、簡単ですが、独自のニュアンスもあります。 これらのアルゴリズムにしか精通していない人のために、記事の最後にある有用な資料にまず慣れることをお勧めします。
2つのアルゴリズムの理論はHabréと他のサイトにありますが、説明のコメントがあるantアルゴリズムのオープンコードは実際には見つかりませんでした。擬似コードがあり、その一部があります。 MATLABのシミュレーションアニーリングコードは以前にレイアウトされましたが、他のタイプの最適化と比較するために低速です。 したがって、彼は自分で書き、時々速度を上げました。 私の意見では、小さなコードでアルゴリズムの構造を認識しやすいため、組み込みの固有関数を使用せずに両方のアルゴリズムを作成しました。 混乱する可能性のある場所では、より詳細なコメントをしようとしました。 これに基づいて、私は理論に入るつもりはありません、私は以下を与えるだけです:
シミュレーテッドアニーリング
シミュレーテッドアニーリング法は、制御された冷却下での材料体の挙動を反映しています。 研究が示しているように、溶融材料の凝固中、その温度は完全に結晶化する瞬間まで徐々に低下するはずです。 冷却プロセスが速すぎると、材料の構造に大きな不規則性が形成され、内部応力が発生します。 通常以上のレベルでの身体のエネルギー状態の迅速な固定は、最適化アルゴリズムの局所最小点への収束に似ています。 身体の状態のエネルギーは目的関数に対応し、このエネルギーの絶対最小値は大域的最小値に対応します[1] 。
Antアルゴリズム
巡回セールスマン問題の近似解を見つけ、グラフ上のルートを見つける同様の問題を解決するための最も効果的な多項式アルゴリズムの1つ。 このアプローチの本質は、コロニーから電源への道を探すアリの行動モデルを分析して使用することであり、メタヒューリスティックな最適化です[2] 。
antアルゴリズムには多くの修正があります。 フェロモンの更新のどこか、「エリート」アリのいる場所、開始時のアリの異なる場所。 コードでは、何かをコメントアウトし、コメントを外します。
シミュレーテッドアニーリング。 コメント付きの完全なコード
% ( ) %-------------------------------------------------------------------------- tic % clearvars -except cities clearvars % ----------------------------------------------------------------- % - m = 100000; % ---------------------------------------------------------------- % Tstart = 10000; % Tend = 0.1; % T = Tstart; % S = inf; % n = 100; % ------------------------------------------------------------------- % dist = zeros(n,n); % ------------------------------------------------------------------------- % (x,y) cities = rand(n,2)*100; % ROUTE = randperm(n); % for i = 1:n for j = 1:n % dist ( ) dist(i,j) = sqrt((cities(i,1) - cities(j,1))^2 + ... (cities(i,2) - cities(j,2))^2); end end % , - for k = 1:m % Sp = 0; % , ROUTEp - % % ROUTEp = ROUTE; % transp = randperm(n,2); % , transp % if transp(1) < transp(2) ROUTEp(transp(1):transp(2)) = fliplr(ROUTEp(transp(1):transp(2))); else ROUTEp(transp(2):transp(1)) = fliplr(ROUTEp(transp(2):transp(1))); end % () for i = 1:n-1 Sp = Sp + dist(ROUTEp(i),ROUTEp(i+1)); end Sp = Sp + dist(ROUTEp(1),ROUTEp(end)); % , ... % , , if Sp < S S = Sp; ROUTE = ROUTEp; else % 0 1 RANDONE = rand(1); % P = exp((-(Sp - S)) / T); if RANDONE <= P S = Sp; ROUTE = ROUTEp; end end % T = Tstart / k; % if T < Tend break; end; end % citiesOP(:,[1,2]) = cities(ROUTE(:),[1,2]); plot([citiesOP(:,1);citiesOP(1,1)],[citiesOP(:,2);citiesOP(1,2)],'-r.') % clearvars -except cities ROUTE S % toc
Antアルゴリズム。 コメント付きの完全なコード
% ( ) % ------------------------------------------------------------------------- tic % clearvars -except cities clearvars % ----------------------------------------------------------------- % - ( ) age = 50; % - countage = 30; % - n = 30; % ----------------------------------------------------------------- % - , 0 % a = 1; % - , 0 % b = 2.5; % ( ) e = 0.5; % Q = 1; % - ( elite ) elite = 1; % ph = 0.01; % ------------------------------------------------------------------- % dist = zeros(n,n); % returndist = zeros(n,n); % ROUTEant = zeros(countage,n); % DISTant = zeros(countage,1); % bestDistVec = zeros(age,1); % bestDIST = inf; % ROUTE = zeros(1,n+1); % ( ) RANDperm = randperm(n); % P = zeros(1,n); % ------------------------------------------------------------------------- % (x,y) cities = rand(n,2)*100; % tao = ph*(ones(n,n)); % for i = 1:n for j = 1:n % dist ( ) dist(i,j) = sqrt((cities(i,1) - cities(j,1))^2 + ... (cities(i,2) - cities(j,2))^2); % nn ( ) if i ~= j returndist(i,j) = 1/sqrt((cities(i,1) - cities(j,1))^2 + ... (cities(i,2) - cities(j,2))^2); end end end % for iterration = 1:age % ( ) for k = 1:countage % ****************** ****************** % % % ROUTEant(k,1) = randi([1 n]); % ( ), - % - ROUTEant(k,1) = RANDperm(k); % 1- % ROUTEant(k,1) = 1; % , % , , % % if iterration == 1 % ROUTEant(k,1) = randi([1 n]); % % ROUTEant(k,1) = RANDperm(k); % % ROUTEant(k,1) = 1; % else % ROUTEant(k,1) = lastROUTEant(k); % end % ********************************************************************* % , , for s = 2:n % ir = ROUTEant(k,s-1); % ( ) , % : tao^a*(1/S)^b % 1/S - returndist. % (- * % * - ) , , % . % . : % for c = 1:n % P(1,c) = tao(ir,c).^a * returndist(ir,c).^b; % end P = tao(ir,:).^a .* returndist(ir,:).^b; % ( k- ) % n , , % % , , % 0, % P(ROUTEant(k,1:s-1)) = 0; % ( = 1 ) P = P ./ sum(P); % RANDONE = rand; getcity = find(cumsum(P) >= RANDONE, 1, 'first'); % - , if isempty(getcity) == 1 disp ' !' end % s- k- ROUTEant(k,s) = getcity; end % k- ROUTE = [ROUTEant(k,1:end),ROUTEant(k,1)]; % S = 0; % k- for i = 1:n S = S + dist(ROUTE(i),ROUTE(i+1)); end % k- , k- DISTant(k) = S; % S if DISTant(k) < bestDIST bestDIST = DISTant(k); bestROUTE = ROUTEant(k,1:end); end % "" k- ( % , % ) % lastROUTEant = ROUTEant(1:end,end); end % ----------------------- --------------------- % "" - tao = (1-e)*tao; for u = 1:countage % u- ROUTE = [ROUTEant(u,1:end), ROUTEant(u,1)]; % for t = 1:n x = ROUTE(t); y = ROUTE(t+1); % if DISTant(u) ~= max(DISTant) % % tao(x,y) = tao(x,y) + Q / DISTant(u); else % tao(x,y) = tao(x,y) + (elite*Q) / DISTant(u); end end end end % citiesOP(:,[1,2]) = cities(bestROUTE(:),[1,2]); plot([citiesOP(:,1);citiesOP(1,1)],[citiesOP(:,2);citiesOP(1,2)],'.r-') clearvars -except cities ROUTE bestDIST bestROUTE ROUTEant toc
それでは、比較してみましょう、最初の30都市を生成します。
シミュレーテッドアニーリング:
パラメータ:
- 都市の数-30
- 初期温度-10,000
- 最終温度-0.01
- 温度式-初期温度/ k回目の反復
- 反復回数-100 000
- 受入確率関数-exp(-ΔE/ T)
- 潜在的なルート(生成ファミリ)の決定-ベクトルの一部(現在のルート)は、一様分布によってランダムに選択された2つの番号から変換されます。
次に、同じ座標でのantアルゴリズムの動作を見てみましょう。
Antアルゴリズム:
パラメータ:
- 反復(世代)の数-60
- 世代のアリの数は30です
- 都市の数-30
- アルファ(係数。フェロモンの方向)-0.85
- ベータ(パスの長さの方向係数)-3.8
- e(係数。フェロモンの蒸発)-0.5
- エリート(エリートアリの数)-いいえ
- 最初の都市でのアリの位置は、繰り返されることなく異なります。 都市の数=世代ごとのアリの数
- フェロモンの更新-グローバル(フェロモンは第1世代の経過後に更新されます)
- ある頂点から別の頂点への遷移の確率-
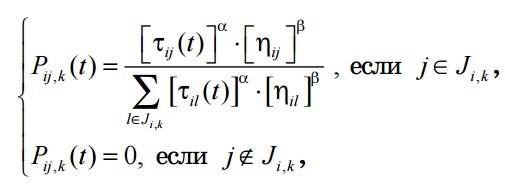
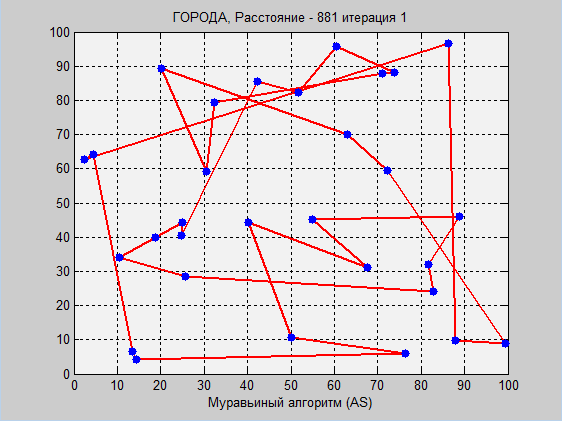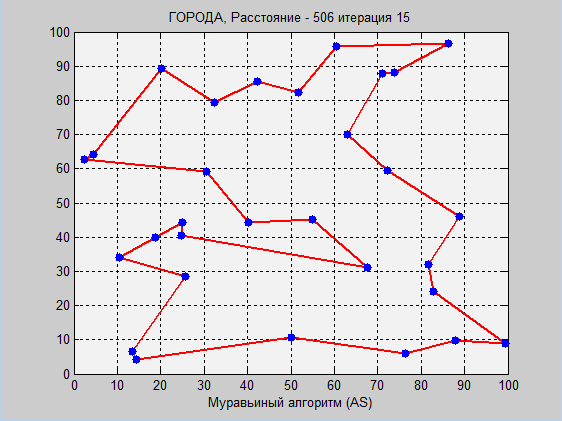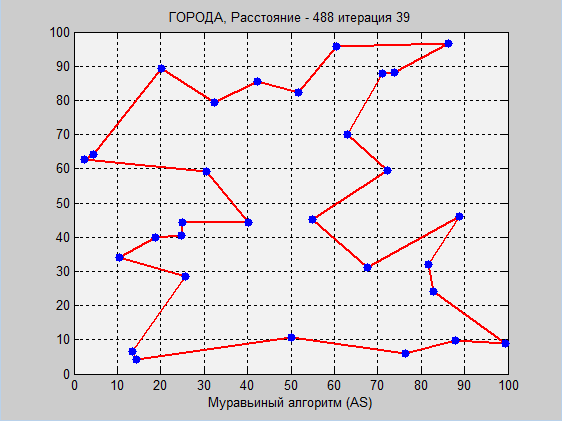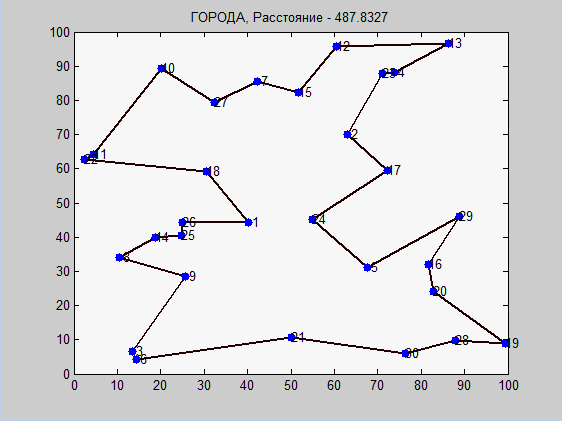
これは、2つのアルゴリズムの視覚的な作業です。 繰り返しになりますが、詳細な説明(特にantアルゴリズムの説明)はコードのコメントにあります。
シミュレーテッドアニーリングでは、20,000回の反復ですでに最適値が見つかったため、温度が十分に低くなると、新しいルートに切り替わる確率が大幅に低下したため、アルゴリズムは「停止」します。 ここで、停止基準を入力できます。 初期温度が高いほど、最適なルートに到達する可能性が高くなり、より多くの反復が完了しますが、グローバル最適が見つかるという事実からはほど遠いです。
antアルゴリズムでは、すべてが異なります。 antアルゴリズムの主な利点は、停止しないこと、常により良い方法を探すことです。 無限の反復(世代)では、グローバルな最適値を見つける確率は1になる傾向があります。しかし、最初に問題が発生しました。どの初期パラメーターを選択するのですか? 回答:選択方法による。 再び最適化。 私は、特定の座標ではない遺伝的アルゴリズムを使用して、アリ最適化のこれらのパラメーターを最適化しました。 他の座標があり、都市の数は50でした。実際に良好な収束を得ることなく、この例にほぼ対応するいくつかのパラメーターを取得しました。
私は1つのテストだけでは行けないので、一連のテストの表を用意しました。

2つのアルゴリズムの安定性は明らかですが、antアルゴリズムの平均値からの広がりは小さくなっています。
次に、生成された100都市ごとに2つのアルゴリズムの動作を見てみましょう。
シミュレーテッドアニーリング:
パラメータ:
- 都市の数-100
- 開始温度-42,000
- 最終温度-0.01
- 温度式-初期温度/ k回目の反復
- 反復回数-420 000
- 受入確率関数-exp(-ΔE/ T)
- 潜在的なルート(生成ファミリ)の決定-ベクトルの一部(現在のルート)は、一様分布によってランダムに選択された2つの番号から変換されます。
次に、同じ座標でのantアルゴリズムの動作を見てみましょう。
Antアルゴリズム:
パラメータ:
- 反復数(世代)-50
- 世代のアリの数は100です
- 都市の数-100
- アルファ(係数。フェロモンの方向)-1
- ベータ(経路長の方向係数)-3
- e(係数。フェロモンの蒸発)-0.5
- エリート(エリートアリの数)-いいえ
- 最初の都市でのアリの位置は、繰り返されることなく異なります。 都市の数=世代ごとのアリの数
- フェロモンの更新-グローバル(フェロモンは第1世代の経過後に更新されます)
ここで、パラメータは「目で」見ました。
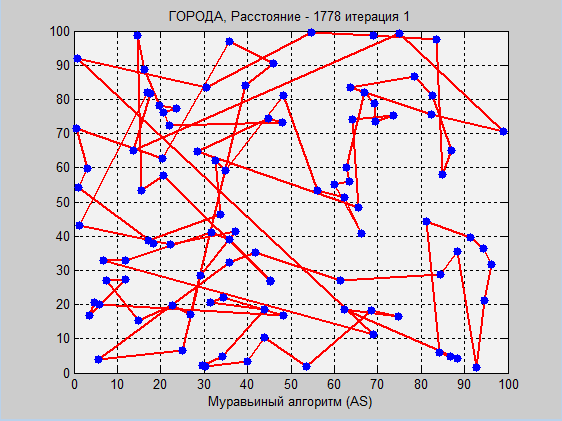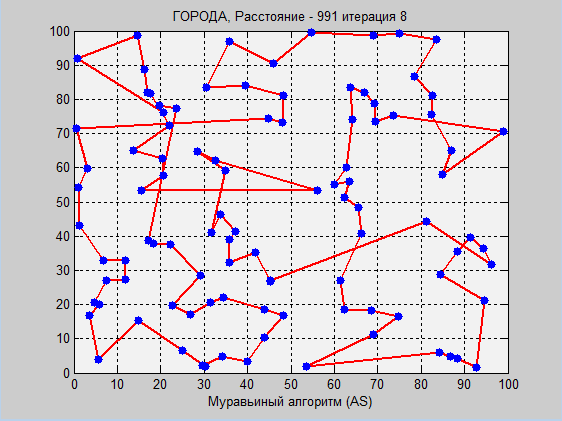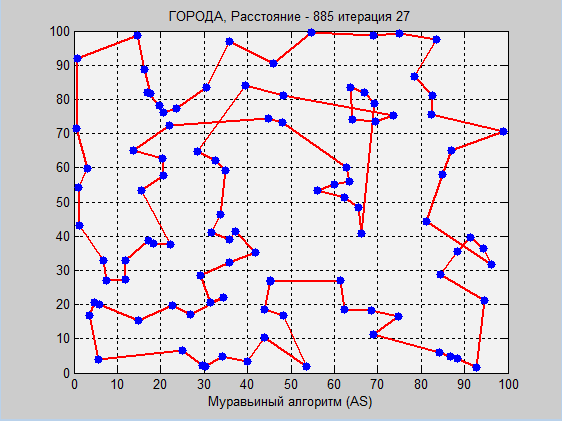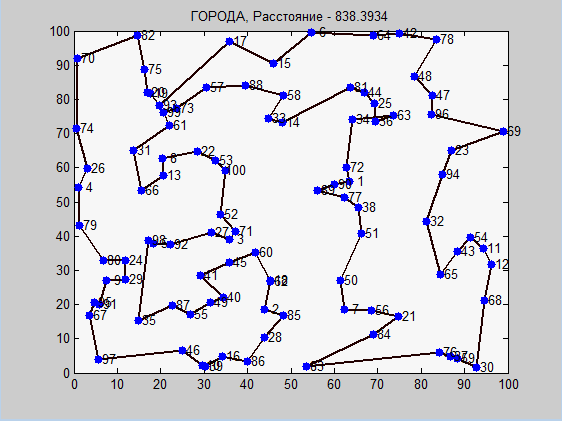
再び、antアルゴリズムはより良い結果を示しましたが、一連のテストの表をもう一度見てみましょう。
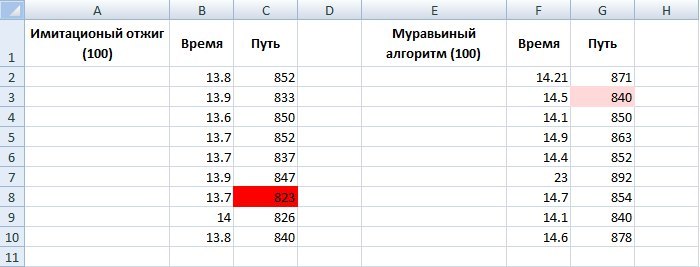
ここでは、シミュレーテッドアニーリングがはるかに進んでいます。 一般に、この記事を読む前は、模倣アニーリングに懐疑的でした。 私が関与しているトレーディングシステムの開発とその最適化では、アニーリング法は適切ではありません。なぜなら、それは私たちにとって重要なローカル最適ではなく、その周りの「散布」だからです。 条件付きの例:ある紙には15日の移動平均があり、その年の収量は10,000で、14日(-1000)でした。 ここでは、最適なパラメーターの周りで利益が均等に減少することが重要です。 したがって、さまざまな状況で-さまざまな最適化。
巡回セールスマンの問題に関しては、「純粋な」競争に参加していなくても(アリアルゴリズムに適切なパラメータを選択する方法がなかったため)、模倣アニーリングに勝利しました。 停止基準を追加することで、標準偏差に大きな変化のない同じ距離を2.5秒で達成できますが、これはantアルゴリズムについては言えません。 かなりの部分がここに到達しなかった一連のテストによると、antアルゴリズムは最大50の都市で見事に機能し、その後「ドリズリング」を開始し、最適化時間が大幅に遅くなります。これは基本的に論理的です。 ただし、ゆっくりとは言っても、彼は自信を持ってグローバルな最適化に向かっています。
どこか深い所で、私はまだantアルゴリズムのパフォーマンスを向上させたいです。 たぶんそれが彼がどこかで間違いを犯したという感じで、1つではないのです。 したがって、興味のある人、そしてこの方向に進んでいるだけの人が参加します。 アルゴリズムと資料の最適な送信方法の両方に関する提案を含むコメントを書いてください。
それまでの間、今日の勝者を見てください。 500都市、86秒の最適化(そしてこれは限界からはほど遠い)。
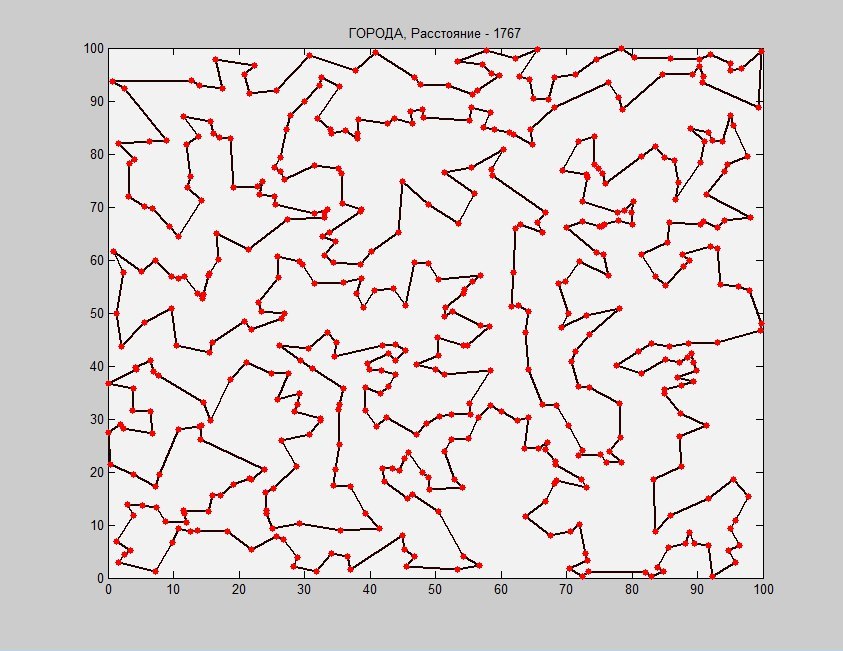
とてもクール!
アリのアルゴリズムは追いつくかどうか? 彼の遺伝的追い越しはありますか? 誰がより効果的でしょうか? これおよびその他については、以下の出版物をご覧ください。
便利なもの:
» antアルゴリズムに関するビデオ(ロシア語)
» シミュレーテッドアニーリングに関するビデオ(ロシア語)
» Antアルゴリズムに関する記事(ロシア語)
» 模倣アニーリングに関する記事(ロシア語)