Stepic.orgでは、適応学習システムについて引き続き話し合っています。 このシリーズの最初の紹介はここにあります 。
この記事では、推奨システム(適応性の基礎となる)の構築について説明します。 ユーザーデータの収集と処理、遷移グラフ、ハンドラー、ユーザーの反応の評価、結果の生成について説明します。
線形回帰、正則化を思い出し、この場合、他の回帰ではなく、リッジ回帰を使用する方が良い理由を理解しましょう。
一般的な言葉
Stepic.orgの推奨システムは、ユーザーが以前興味を持っていたものに基づいて、新しいレッスン(教育コンテンツ)を提供します。 このため、彼女はさまざまな方法を使用してコンテンツを検索します。コンテンツは、ユーザーが既に学習したものに似ているか、似ていないが一般的には興味深いものです。
これらの各メソッドは個別の関数( ハンドラー )として設計されており、そこに定められた原則に従ってレッスンのリストを抽出し、ユーザーに合う方法に応じて重みでラベル付けします。 これらのハンドラー関数の詳細な説明を以下に示します。
推奨システムは、さまざまな状況に適用できます。 2つの主なケース:
- 特定のユーザーに対する通常の推奨事項。メインページおよび[推奨レッスン]タブに表示されるほか、メールに送信されることもあります。
- コース外のレッスンを終えた後にユーザーに表示されるコンテキスト推奨 (つまり、次に続くものの固定のレッスンがない場合のレッスン)、次に見るべきもののヒントとして。
推奨事項に加えて、ユーザーには、この特定のレッスンが提供された理由に関する情報も表示されます。 この情報は、いくつかの直感が各関数ハンドラーに埋め込まれているため、簡単に抽出できます。そのため、推奨の理由を復元できます。
ユーザーデータ
Stepic.orgの学習プロセスでは、ユーザーはかなりのデジタルフットプリントを残します。 彼の進行状況に関する情報に加えて、さまざまなステップ(ステップはコンテンツの基本単位です。ステップはより大きなレッスンに結合されます)、問題を解決しようとしたとき、結果、およびビデオの視聴方法:速度セットについての情報も保存されますそして彼が止めた場所と巻き戻す場所。
次の情報は、基本的なレコメンダーシステムにとって最も興味深いものです:ユーザーが興味を持っているタグ(つまり、レッスンがテストされた知識の領域)、ユーザーが行ったレッスン、学習したレッスン、および推奨がコンテキストに応じている場合は現在のレッスン。
特定のユーザーに関する情報に加えて、保存されたデータは、ユーザーとコンテンツとの相互作用に関する情報と見なすことができます。 この情報を集約して使用する方法の1つは遷移グラフであり、これについては後で詳しく説明します。
変換グラフ
ユーザーがコンテンツをどのように学習するか、より頻繁に、より頻繁に、何をスキップするか、どの素材が戻るか、そして重要なことには、どの順序で表示されるかを学ぶことはしばしば役立ちます。 ユーザーアクションに関するログを使用すると、これらの質問に簡単に答えることができます。 このために、 遷移グラフ ( プロセスマップ )、つまり、頂点がコンテンツの単位(ステップやレッスンなど)になるような有向グラフを使用し、アークの重みはこれらのコンテンツ単位間の遷移の数を示します。
ログ内の各ユーザーアクションにはタイムスタンプがあります。 アクションは、「表示済み」(ステップを開いた)、「成功した試行」(問題を解決した)、または「コメントした」(コメントを残した)など、さまざまなタイプにすることもできます。 ステップに関するユーザーのアクションに関心があります。ステップは、これらのステップが属するレッスン、さらにはレッスンをマークしたタグに簡単に一般化できます。
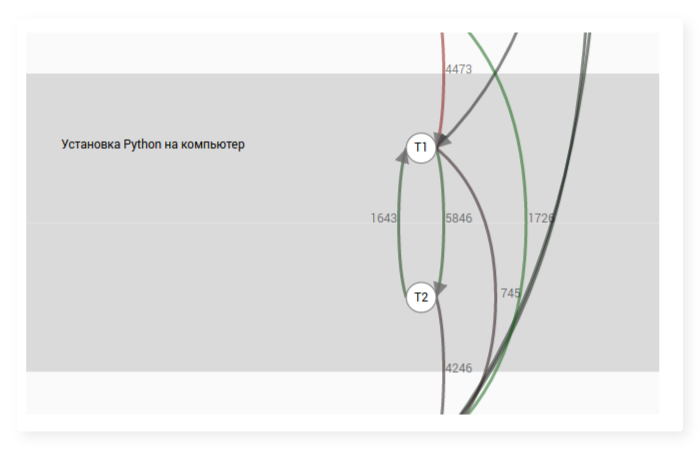
視覚的には、遷移グラフは一連の物質的な頂点(ステップなど)として想像でき、その間にいくつかのアークがあります。 2つのステップの間にアークが存在するということは、それらを次々と表示するユーザーがいることを意味します。 各アークには、そのようなユーザーの数を含むラベルがあります。 コース内の1つのレッスンのステップの遷移グラフの例:
遷移グラフを作成するプロセスは簡単です:各ユーザーについて、ステップに関連するすべてのアクションを考慮し、それらを時間でソートし、ステップのペアごとに、一方のアクションの直後に他方のアクションを実行した回数をカウントします。 次に、すべてのユーザーの頻度を要約し、共通の遷移グラフを取得します。
最初に、ステップバイステップのグラフを導入しました。これにより、教師は学生がコース教材をどの順序で学習するかを知ることができます。 分析を簡単にするために、コース内のステップ間の遷移の平均頻度を計算し、遷移が予想よりも頻繁に発生した場合は最終グラフのエッジを緑色に、予想よりも少ない場合は赤色に、まれな遷移も除外します。
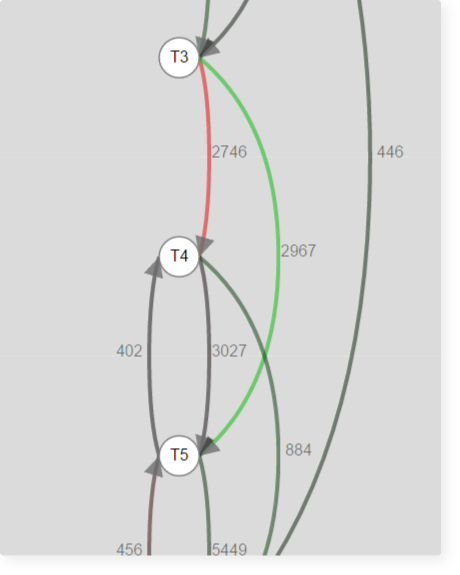
コースのいずれかの遷移グラフのフラグメント:
このフラグメントは、T4理論のステップが通常よりも頻繁にスキップされ、次のステップに進むことを示しています。
さらに、推奨システムでこれを使用するために、ステップだけでなく、レッスンとタグによって遷移グラフを作成し始めました。 レッスンの遷移グラフは、ステップの場合と同じ原理に基づいて作成されます。ステップのアクションだけが、これらのステップが属するレッスンのアクションと見なされます。 タグの場合、プロセスは同様です。ステップを含むアクションは、タグを含むアクションに変換されます。
ハンドラー
ここでは、それぞれが独自の推奨方法を実装するハンドラー関数をリストします。 ハンドラーはユーザーをパラメーターとして受け入れ、推奨事項がコンテキストに基づいている場合は、ユーザーが現在行っているレッスンです。 ハンドラーはユーザーに戻ります レッスンのリスト。それぞれが0〜1の重みに対応します。重みが大きいほど、推奨事項は高くなります。
。
ユーザーにお勧めしたい 特定のタグのレッスン。ユーザーが学習したレッスンの割合は
。 遷移グラフがない場合、すべてのレッスンに重みが付けられます
。 グラフがある場合、レッスンごとに、この重みは、ユーザーが渡した最も近い前のレッスンまでのグラフ内の距離で除算されます
。 このように、ユーザーは、遷移グラフにある資料を自分が既に学習している資料からそれほど遠くない場所に移動することに興味があるという考えが実現します。
ユーザーにとって興味深いタグを使用したレッスン-ハンドラーは、ユーザーが既に学習したタグでマークされたレッスンを推奨します。 これを行うには、上記のタグの推奨事項、レッスンの重みを使用します
ユーザー向け
なります
。
不完全なレッスン -推奨されるのは、ユーザーが開始したレッスンと終了しなかったレッスンで、ユーザーが学習したレッスンの大部分よりも大きな重みがあります。
レッスンシェア
ユーザーから渡された
。
人気のあるレッスン -ハンドラーはユーザーに関する情報を使用しませんが、過去1週間にプラットフォームで最も人気のあるレッスンを推奨します。 重みは人気に直接比例します。
どこで
-レッスン番号
人気のあるレッスンのリスト。
レッスンパス -ユーザーが合格したレッスンを含むパスが使用されます。合格後にレッスンをお勧めします。重量が少ないほど、すでに合格したレッスンからさらにレッスンが得られます。
どこで
-レッスンからの距離
ユーザーが渡した、旅行中の最も近い前のレッスンへ
。
タグナビゲーショングラフ -ユーザーが興味を持つタグの後に学習するタグを使用した推奨レッスン。 重みは、タグのユーザーの進捗状況と、タグ間の遷移の相対的な頻度に依存します。 させる
-ユーザーが学習したタグからタグへの移行の頻度
。 次に、レッスンのために
タグ付き
体重ユーザーの推奨事項
なります
。
類似ユーザーからのタグに関するレッスン (協調フィルタリング)-ユーザーが関心を持つタグに基づいて、類似するユーザーが特定され、学習したタグを含むレッスンが推奨されます。 現在のユーザーにしましょう
彼に似たユーザーを見つけた
、およびそれらの間の類似性の尺度は
(0から1の間で、それが大きいほど、ユーザーはより似ています)。 それからレッスン
勉強したタグでタグ付け
重量で推奨されます
。
レッスン遷移グラフ (コンテキストの推奨がある場合のみ)-ハンドラーは、現在の遷移グラフに従うレッスンを推奨します。重みは、現在のレッスンと推奨されるレッスン間の相対的な遷移頻度に依存します。 現在のレッスンからレッスンへの移行の場合
相対頻度で実行
それから
。
- レッスンパス(コンテキストの推奨事項のみ) -推奨されるのは、どのパスでも現在のレッスンに従うレッスンです。重みはレッスン間の距離に反比例します。
どこで
-レッスンからの距離
現在のレッスンまで。
- 集合内の以前のすべてのハンドラが必要なレッスンよりも少ないレッスンを推奨した場合、ランダムレッスンが推奨に追加され、そのようなレッスンの重みは0です。
わかった? よし、進みましょう。

ユーザー応答の評価
推奨がどの程度成功したかを理解するために、推奨を表示した後、ユーザーがリンクをクリックしたかどうか、およびユーザーが最終的に学習したレッスンの部分(0から1までの値)を記録します。 同時に、ユーザーはレッスンがアドバイスされた理由を見つけて(オプションはハンドラーに対応)、推奨事項に興味がないとマークする機会があります。
示されている各推奨事項の結果として、特定の番号を一致させることができます。 推奨事項の拒否に対応し、
-レッスンを学習せずにリンクをクリックする、
-リンクをたどってレッスンを完了する
前に
-不完全なレッスン学習、および
-反応の欠如。
発行の形成
そのため、複数のハンドラーからレッスンのリストを取得しました。各レッスンには0〜1の重みがあります。ハンドラーが成功すればするほど、この推奨事項が評価されます。 問題は、それらをどのように組み合わせるのが最善ですか?
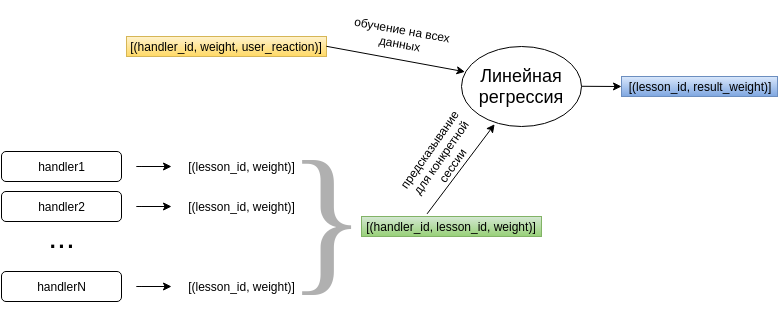
レッスンごとに、アドバイスしたハンドラーの重みを単純に加算または乗算することができます。 しかし、これは、異なるハンドラーが同等に有用であると考えることを意味し、一般的に言えば、それはまったくそのようにはならないかもしれません。 推奨事項に対するユーザーの反応を使用して、効用係数を使用して各ハンドラーを評価したいと思います。 単純な線形回帰はこれらの要件を満たします。
回帰モデルは、さまざまなハンドラーの推奨事項がユーザーによって評価された方法に関する累積データを使用してトレーニングされます。 これに基づいて、モデルはハンドラーの重みのベクトルを形成します。 さらに、生徒に何かを推奨する必要がある場合、各レッスンの回帰モデルは、それを提供したハンドラーの重みに訓練されたパラメーターベクトルをスカラー倍し、各推奨レッスンの結果の重みを与えます。
素材を深く掘り下げたので、回帰モデルを正式に説明しましょう。 線形回帰とは何かをよく知っている場合は、次のセクションをスキップしてください。
線形回帰
行列があるとします その行
観測と呼ばれ、列は因子 、 ターゲットまたは従属変数の値の列
。 回帰モデル
どこで
-モデルパラメーター、および
-因子に対するターゲット変数の依存性が線形である場合、すなわち、
。
通常、便宜上 ( 定数 )は、観測行列に単位の列を追加することにより、合計記号の下に入力されます。
すべてのために
。
これらの表記法を使用すると、線形回帰モデルは次のように記述できます。 。 この問題の解決策はコラムです
、実際の値からの予測値の二乗偏差の合計を最小化します。
。
この近似法は最小二乗法と呼ばれ、線形回帰問題を解くという文脈で最も広く使用されています。
この場合、観測値、つまり行列の行と見なすことができます 、ハンドラーがレッスンに割り当てたこれらの重みの観察の要因として、およびターゲット変数の値として、ユーザーの推奨評価として推奨レッスン。
だから、レッスンのために ユーザーに推奨
それぞれ、およびハンドラー用
観測行列
およびターゲット変数の値の列(ユーザー応答)
次のようになります。
ベクトル 、ユーザーの反応を予測する際に最小限のエラーを与えますが、各ハンドラーの個別の重みが含まれており、それによって推奨事項を乗算する必要があります。 ハンドラーの1つの重量が比較的大きい場合、このハンドラーは推奨事項に積極的に貢献し、その逆も同様です。
推奨システムが機能するために、推奨に対するユーザーの反応に関するデータに基づいて回帰モデルが定期的に再トレーニングされます。 SciPyライブラリを使用してこの問題を解決し、列を見つけます。 。 このライブラリは、線形回帰問題の解決策を既に実装しています。
わかった? まあ、少し残った。

正則化
ハンドラーの重みの列を見つけた線形回帰推奨システムを実装した後 予測からのユーザーの実際の応答の偏差の二乗を最小化する(
)、1つのハンドラーの重みが徐々に無制限に増加し、残りが減少し、最終的にこのハンドラーの結果からほぼ排他的に発行が行われることに気付きました。 この効果は正のフィードバックと呼ばれ、システムの結果の偏差がその後の作業に影響するという事実によって特徴付けられ、さらに、結果はこの偏差に向かってシフトします。
さらに、ハンドラーはユーザーアクティビティに関する非常に類似した情報を使用できるため、データ内の因子の多重共線性の問題が発生する可能性があり、マトリックスの弱い分離が必要になります そして、結果として、ソリューションの不安定性。
その結果、トレーニング対象のデータに小さなエラーを与え、実際のデータに大きなエラーを与えるソリューションが得られます。 この状況は、モデルの過剰適合と呼ばれます 。
正則化は、再トレーニングの問題の解決策と見なすことができます。 The Elements of Statistics Learningによると、主な正則化方法は、なげなわ(LASSO、最小絶対収縮および選択演算子)とリッジ回帰 (Tikhonovの再構築、リッジ回帰)です。 これらの方法はどちらも、ベクトルのノルムにペナルティを追加することにより、回帰解の検索中に最小化する式を変更します 。
投げ縄正規化の場合に使用されます -ノルムとソリューションは

リッジ回帰の場合、それが使用されます -規範と解決策は次のようになります
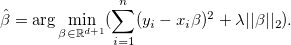
どちらの場合でも、パラメーター 最適化プロセス中に選択されます。
Lassoメソッドによる正則化を使用すると、すべての重みが減少します 、すでに比較的小さいものはゼロに等しくなります。 したがって、なげなわメソッドは、重要な要素の選択(機能選択)に適しています。
リッジ回帰法も因子の重みを減らしますが、以下の場合を除き、それらをゼロに減らすことはありません。 。
Andrew Ngによると、因子の数がトレーニング観測の数を大幅に超える状況では、投げ縄正規化はリッジよりもうまく機能します。 反対の状況では、リッジ回帰がより適切です。
したがって、リッジ回帰は私たちの場合により適しています。 その実装はSciPyライブラリにも存在し、非常に満足しています。
おわりに
この記事では、Stepic.orgで教育コンテンツの推奨システムを実装する方法を見つけました。 たぶん、それは簡単ではなかったかもしれませんが、あなたは成功しました! (もちろん、この場所までスクロールしなかった場合は、戻って読むことをお勧めします)
推奨システムの実際の動作は、 https://stepic.org/explore/lessonsで確認できます。学習するための推奨レッスンがリストされています。 しかし、プラットフォームに入るのがこれが初めての場合、推奨事項は特に関係ない場合があります。
このシリーズの次の最終記事では、Stepicaの適応システムを直接検証し、実行された作業の結果(予測の精度、ユーザー設定、統計の評価)について説明します。
そして最後に、私は尋ねたいです: あなたは適応型オンライン教育を信じていますか? 従来のコースに取って代わりますか? 最もインテリジェントな推薦システムは、実際の教師よりも優れた教育コンテンツを個人に勧めることができますか?