
スティーブン・ウルフラムの「 ラマヌジャンとは誰か? 」翻訳後。
出版物の翻訳と準備にご協力いただいたPolina Sologubに感謝します。
内容
素晴らしい手紙
物語の始まり
ハーディは誰でしたか?
手紙とその結果
ラマヌジャンのワークスタイル
重要なものを見る
真実または説明
ケンブリッジに行く
ケンブリッジのラマヌジャン
次に起こったこと
ハーディはどうなりましたか?
数学ラマヌジャン
事実はランダムですか?
ラマヌジャンの自動化
現代のラマヌジャン?
RamanujanにMathematicaがある場合はどうなりますか?
今週、映画「The Man Who In Know Infinity 」( Manjul BhargawaとKen Onoが昨秋私に見せてくれた)が来たので、私は彼の主人公であるSrinivas Ramanujanについて書くしかありませんでした。

素晴らしい手紙
彼らは以前は普通の郵便で来ていました。 今-メールで。 長年にわたり、世界中からの手紙が集まってきて、素数、相対性理論、人工知能、意識、その他多くのことについての大胆な発言を含んでいます。 これらのメッセージを見て、私はラマヌジャンの歴史を思い出し、少なくともそれらに目を通すために私のアイデアとプロジェクトを常に延期しました。
1913年1月31日頃、イギリスのケンブリッジ出身の数学者が、次のように始まるカバーレター付きの書類のパッケージを受け取りました。 .... ”そして彼は続けた:彼は数学における発散級数の理論で“驚くべき”進歩を遂げ、 素数分布の長年の問題を解決したと書いた。カバーレターは次の言葉で終わった。 ここに何か貴重なものがあると判断した場合、定理を公開してほしい...私は経験が浅く、あなたのアドバイスは私にとって貴重です。 ご不便をおかけして申し訳ございません。 敬具、S。ラマヌジャン 。
これに続いて、数学分野の多くから少なくとも11ページの技術的結果が得られました(そのうち2つは失われました)。 一見すると、すべての正の数の合計が-1/12であるという不条理なステートメントがありました。


数学における一種の実験的アプローチの使用を示唆する声明がありました。

このような式を含む、よりエキゾチックなページがありました:

これは何ですか 彼らはどこから来たのですか? 彼らは正しいですか?
概念自体は、大学の分析を勉強した人になじみがあるはずです。 ただし、複雑な大学レベルの演習だけが手紙に添付されたわけではありません。 よく見ると、手紙のすべてのページで完全に異常で予期しないことが起こります。それは異なるレベルの数学のようです。
現在、 MathematicaまたはWolframを使用できます| アルファ また、質問を入力してすぐに回答を得ることができます。
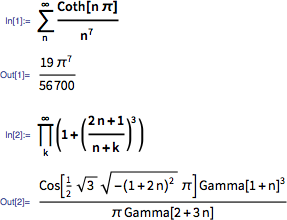
公式が正しいことを確認できます(1913年のG. H. Hardyとして)。 しかし、どのような人がそれらを引き出すことができますか? そしてどうやって? それらは、全体像の一部なのでしょうか、ある意味では、単に数学の混randomとしたランダムな事実なのでしょうか?

他のページ 



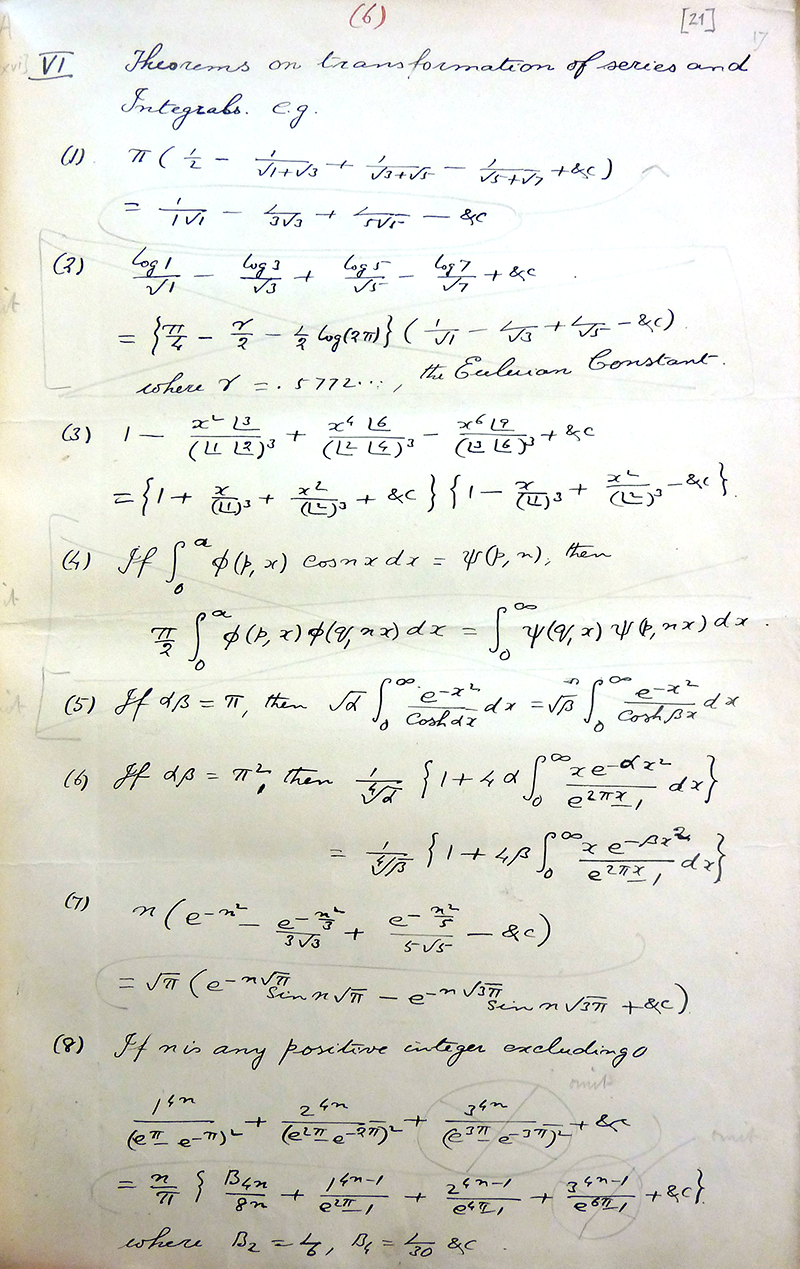







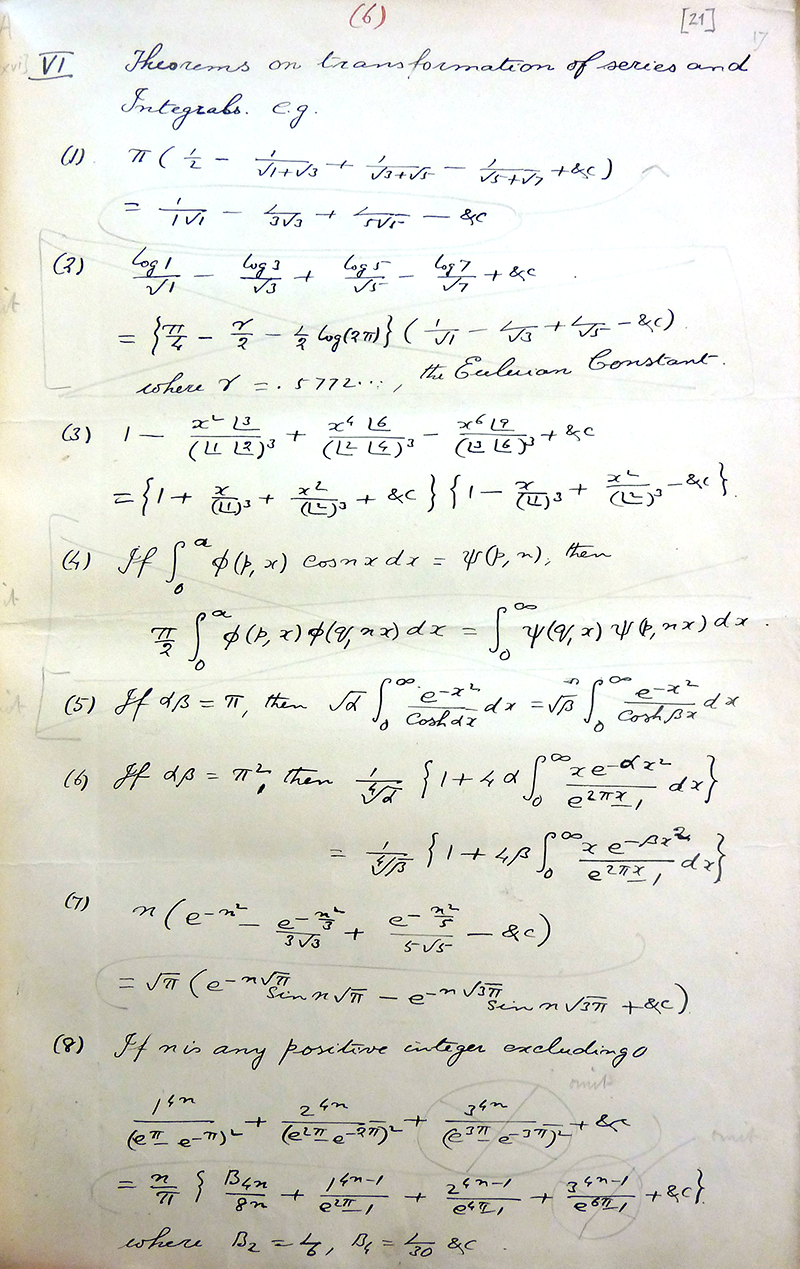



物語の始まり
この手紙の後ろには、 ラマヌジャンの驚くべき物語があります。
彼は1887年12月22日にインドの小さな町で生まれました(これは、ハーディに手紙を書いたとき「約23歳」ではなく、 25歳だったことを意味します)。 彼の家族は裕福ではなく、バラモンカースト(司祭、教師など)に属していました。 更新された学校システムでの試験の結果によると、ラマヌジャンは10歳という早い時期に明らかに他の企業の中で際立っていました。 彼はまた、彼の例外的な記憶のために有名でした。彼は、 サンスクリット語の語根だけでなく、 パイの数字を暗唱することができました。 彼が17歳で高校を卒業したとき、彼は大学の奨学金を与えられました。
高校では、ラマヌジャンは数学を独学で学び始め、 オイラー定数の数値推定とベルヌーイ数の性質の独自の研究を行いました。 彼は幸運にも16歳(当時、インターネットのずっと前に!)に、1,055ページからなる驚くほど優れた完全な(少なくとも1886年の) 高校生向け数学の要約のコピーを受け取った! この本は、ケンブリッジでの試験に備えて3年間の数学プログラムで教師が書いたもので、「事実のみ」スタイルの彼の貪欲な形式は、ラマヌジャンがハーディへの手紙で使用したものと非常に似ていました。






ラマヌジャンが大学に進学する頃には、彼は数学だけをやりたくて、その結果、他の試験に失敗して逃げたので、母親は行方不明者について新聞に手紙を書かなければならなかった。

ラマヌジャンはマドラス(現在のチェンナイ )に移り、そこで様々な大学で勉強しようとしたが病気であり、その結果数学の独立した研究を続けた。 1909年、彼が21歳のとき、母親は当時の習慣に従って、数年後に彼と一緒に暮らし始めたヤナキという10歳の少女と結婚式を取りました。
ラマヌジャンは数学の個別指導を行うことで自らを支えましたが、彼はすぐに数学者としてマドラスの近くで知られるようになり、最近発表されたインド数学学会誌に掲載され始めました。 1911年に公開された彼の最初の記事は 、1843年からの彼の記事で使用されたベルヌーイ数 (Ada Lovelaceと同じベルヌーイ数(記事「 Ada Lovelaceの歴史を解き明かす( 史上初のプログラマー) 」を参照)の計算特性に捧げられました分析機について)。 彼の結果はそれほど印象的ではありませんでしたが、ラマヌジャンのアプローチは興味深く、独創的でした。連続(「数値とは?」)数学と離散(「因数分解は簡単」)数学を組み合わせました。




ラマヌジャンの数学の友人が奨学金を得ることができなかった後、彼は仕事を探し始め、1912年3月にラマヌジャンは会計士としてマドラスの港に来ました 。 彼の上司-主任会計士-学術数学に興味があり、彼の生涯の支持者になりました。 当時のマドラス港の長はイギリスの卓越した土木技師だったので、ラマヌジャンは彼を介してイギリス人駐在員と交流し始めました。 彼らは、彼が「偉大な数学者の能力」を持っているのか、それとも単なる「計算機少年」なのかについて話しました。 彼らはロンドンのヒル教授に手紙を書いた。彼はラマヌジャンが発散した階級についてのいくつかの風変わりな発言を見て、「 ラマヌジャン氏は明らかに数学に興味があり、ある程度の能力さえ持っているが、彼は間違っている 」と述べた 。 ヒルはラマヌジャンにいくつかの本を研究するように勧めました。
ラマヌジャンの友人は彼を支援する方法を探し続けていましたが、英語で手紙を書くのにいくらか助けがあったとしても、彼はイギリスの数学者自身に手紙を書き始めることを決めました。 長い間同志だったハーディ・ジョン・リトルウッドは、 64年後の死の直前に、 H.F。ベイカーとE.V.ホブソンの 2つの名前を挙げましたが、彼が最初に誰に書いたのかは正確にはわかりません。 どちらもあまり良い選択ではありませんでした。ベイカーは代数幾何学の分野で働き、ホブソンはラマヌジャンがやったことからはほど遠い数学的分析に従事していました。 いずれにせよ、彼らの誰も答えなかった。
そして、1913年1月16日木曜日、ラマヌジャンはG.Khに手紙を書きます。 ハーディ。
ハーディは誰でしたか?



ゴッドフリーハロルドハーディは1877年に学校の教師の家族で生まれました。 彼らはロンドン から 30マイル 南に住んでいました 。 彼は最初から、特に数学の分野で最高の学生でした。 1970年代初期にイギリスで育ったときでさえ、そのような高校生は通常ウィンチェスターに移り、その後ケンブリッジに行きました 。 これはまさにハーディがしたことです。 他の人はもう少し有名で、少し厳密ではなく数学的にはあまり向いていませんでした-これらはイートンとオックスフォードです (私が入った)。
ケンブリッジの学部生は、凝ったデザインの微積分問題に取り組んでおり(深刻なスポーツイベントのようでした)、最後に、シニアラングラー(最高得点)から木製スプーン(最低合格得点)に及ぶ学生のランキングがまとめられました。 ) ハーディは自分がコースで最初になると思っていましたが、4位になりました。 彼は数学への厳格で形式的なアプローチが好きで、大陸ヨーロッパで人気が出たという結論に達しました。
英国の学術システムは、当時(および1960年代まで)卒業後、最高の学生が大学のフェローに選出され、一生でも奨学金を受け取ることができるように機能していました。 ハーディは、ケンブリッジ大学で最大かつ最高の科学大学であるトリニティ カレッジに在籍し、1900年に卒業後、大学の学者に選出されました。
Hardyの最初の研究論文は、次のような積分についてでした。

10年間、Hardyは主に計算の複雑さに取り組み、さまざまな種類の積分とその和をとる方法を見つけ出し、収束の問題と統合の限界の順列に対するより厳密なアプローチを主張しました。
彼の作品は素晴らしいものでも幻想的なものでもありませんでしたが、数学的スキルの優れた例となりました。 彼の同僚のバートランド・ラッセルのように 、彼はすぐに新しい分野-半無限の数を研究し始めましたが、彼は長い間彼らと働きませんでした。 その後、1908年に、彼は教科書「 純粋数学のコース 」を書きました-それはその時代には良い、そして非常に成功した本でした(序文では、教科書は能力が「奨学金水準」のレベルに達する学生向けであると言われていました)。
1910年までに、ハーディはケンブリッジ大学の教授の生活に没頭し、学術研究に従事しました。 そして彼はジョン・リトルウッドに会った。 リトルウッドは南アフリカで育ち、最近のシニアラングラーであるハーディよりも8歳若く、多くの点ではるかに起業家でした。 そして1911年、以前は自分自身しか働いていなかったハーディは、リトルウッドとのコラボレーションに参加しました。
男として、ハーディは決して成長しない良い男子学生の印象を作りました。 彼は数学の練習に集中し、構造化された環境での生活を楽しんでいるようでした。 彼は非常に退屈だった-それはクリケットをプレイしながら得点、神の不在の証拠、またはリトルウッドとの彼のコラボレーションのためのルールを書くことに関するかどうか。 典型的なイギリス人である彼は、知性と魅力で自分を表現することができましたが、タフで疎外されていました。 H.ハーディ」、母親と妹だけの「ハロルド」であること。
したがって、1913年の初めまでに、ハーディは立派で成功した英国の数学者であり、リトルウッドとの新しいコラボレーションに興味があり、彼は彼を興味のある数論の分野に引き入れました。 しかしその後、彼はラマヌジャンから手紙を受け取りました。
手紙とその結果
ラマヌジャンの手紙はあまりうまくいきませんでした。彼は、そのようなアイデアや概念を階乗から非整数まで一般化するための有名な分析継続の手法を説明した最初の人物であると考えたようです。 彼は、「 地元の数学者が私と私の仕事を理解できないほど、私の研究でこれらのアイデアを発展させた 」 と述べた。 しかし、カバーレターの後には、9ページ以上が続き、120を超える数学的結果が含まれていました。
最初は、かなりあいまいな声明がありました。 しかし、3ページ目には、和や積分などの公式がありました。 それらのいくつかは、ハーディの作品のそれらに漠然と似ていた。 そして、それらのいくつかは間違いなくよりエキゾチックでした。 それらの一般的な構造はこれらのタイプの数式の特徴でしたが、いくつかの特定の数式は驚くべきものでした:いくつかの事柄は数学的には等しいが、関連することさえ期待できないと述べました。
元の手紙の少なくとも2ページが欠落していました。 私たちが持っている最後のページは、失敗に終わっているようです。ラマヌジャンは、彼の発散級数の理論の成果を説明していますが、すべての正の整数の合計が1 + 2 + 3 + 4 + ... -1 / 12に等しい
ハーディはどのように反応しましたか? まず、彼はリトルウッドに相談しました。 この手紙はデマでしたか? これらの式はすでに知られていましたか、それとも完全に間違っていましたか? 彼らが特定したもの。 しかし、残り-いいえ。 ハーディは後に彼らは正しいに違いないと言った。「 もし彼らが真実でなければ、誰も彼らを思い付く想像力を持たないからだ 」
バートランドラッセルは、翌日、「 ハーディとリトルウッドが2番目のニュートン 、マドラスで年間20ポンドを稼ぐヒンドゥー教の書記官を見つけたと信じているため、大興奮の状態にあった」と書いた 。 ハーディはラマヌジャンの手紙を多くの人々に見せ、その後インドを統治する政府部門に問い合わせを始めました。 このすべてに1週間かかり、その後彼はラマヌジャンに応答の手紙を書きました。その手紙には興奮がはっきりと読まれています。「 私はあなたの執筆と定式化に非常に興味がありました 。」
それから彼は続けた:「 しかし、あなたがしたことの価値を正しく判断する前に、あなたの声明のいくつかの証拠を見なければならないことを理解しなければならない 。」 彼がそれを言ったことに興味があります。 ハーディがこれが真実であることを単に知るだけでは十分ではありませんでした。 彼は証拠を必要としていました。 もちろん、ハーディは自分でそれらを見つけたかもしれません。 しかし、彼は数学者ラマヌジャンの素晴らしさをより完全に把握したかったので、これを書いたように思えます。
ハーディは、その特徴的な正確さを備えた手紙の中で、ラマヌジャンの手紙の内容を3つのカテゴリに分類しました。 新しくて興味深いが、それほど重要ではない。 そして最後に、新しく、潜在的に重要です。 しかし、彼が第三のカテゴリーに帰した唯一のことは、素数の計算に関するラマヌジャンの声明であり、「 ほとんどすべてが、使用した証明方法の精度と厳密さに依存する 」と付け加えた。
ハーディは、明らかに、その時までにラマヌジャンの研究についていくつかの予備研究を行っていた。なぜなら、彼の手紙の中で彼はベルヌーイ数に関する彼の論文に言及していたからだ。 彼は次のように書いています。「 できる限り早くあなたが私に送ってくれることを本当に願っています...あなたの証拠の一部 」、そして最後に「 できるだけ早くあなたから答えを受け取ることを望んで 」という言葉で終わります 。
ラマヌジャンはハーディの手紙に本当に素早く反応しました。 最初に、彼はハーディから「 ロンドンの数学の教授 」と同じ答えを期待していると書いた。彼は単に「 発散系列のtrapに陥らないように」と言った。 その後、彼は厳格な証拠を求めるハーディの希望に応えて、「 証明の方法を示したなら、ロンドンの教授の意見に加わると確信しています 。」と彼は続けて彼の結果に言及します。
1 + 2 + 3 + 4 + ... = -1 / 12
そして、「 …私があなたに言うならば、あなたは私の場所が精神病院にあると答えます 」と付け加えます 。 そして彼は続けます:「 私はあなたがあなたが私の証明方法に従うことができないことをあなたに納得させるためだけにこれについて話している... 1つの手紙に基づいて 」。 彼は彼の最初の目標は結果をテストするハーディのような人を見つけることだと言います。それは奨学金を得ることができることを意味します。なぜなら、「 私はすでに半飢えに住んでいます。私の脳を救うには食べ物が必要です... 」



ラマヌジャンは、「 私の結果は検証されます。 さもないと私の位置が不安定になります」という理由で、すでに知られている最初のカテゴリの結果の存在が彼を非常に幸せにしたという言葉で締めくくります。 言い換えれば、ラマヌジャン自身は結果の正確性について確信が持てず、彼が正しいことを喜んでいた。
彼はどのようにして結果を得たのですか? 後で、これについて詳しく説明します。 しかし、もちろん、彼はあらゆる種類の計算を数値と数式で行いました-実際、彼は実験に従事していました。 そして、彼はおそらくこれらの計算の結果を見て、どれが正しいかを確認しました。 彼がこれをどのように定義したかはまだ不明です。 さらに、最終的に彼の結果のいくつかは水を保持しませんでした。 おそらく彼は、計算の助けを借りて数学的証明と確認の伝統的な方法の両方を使用し、彼の直観を信頼しました。 しかし、彼はこれをハーディに何も言わなかった。
代わりに、彼は結果の詳細について彼に単に連絡し、また彼が与えることができた証拠の断片を引用しました。 ハーディとリトルウッドは意図的に彼の努力を相殺したように見えました。例えば、リトルウッドは彼の結果の一部について次のように書きました。「 (d)-もちろん、これは真実ではありません 。」 しかし、彼らは両方とも、ラマヌジャンが「 オイラー 」なのか、それとも単に「 ヤコビ 」なのか疑問に思っていました。 しかし、リトルウッドは次のように述べています:「素数の材料は間違っています」-ラマヌジャンはゼータ - リーマン関数は複素ゼロを持たないと誤って仮定したという意味で、実際にはそれらの無限に多くがあります(リーマンはこの主題に関する全体の仮説を持っていました)。 リーマン仮説は、彼がまだ学生だったときに楽観的な教師がプロジェクトの仕事としてリトルウッドに提案した、よく知られた未解決の数学的問題です。
ラマヌジャン1 + 2 + 3 + 4 + ... = -1/12の奇妙な表現はどうですか? また、リーマンのゼータ関数にも関連しています。 正の整数の場合、ζ(s)は合計として定義されます
 。 Wolfram言語には興味深い機能があります- ゼータ[s] -複素数の集合全体に範囲を拡大することで取得できます。 次に、正の引数の式に基づいて、 ゼータ[-1]は1 + 2 + 3 + 4 +の合計であると言えますが、 ゼータ[-1]を単純に計算できます。
。 Wolfram言語には興味深い機能があります- ゼータ[s] -複素数の集合全体に範囲を拡大することで取得できます。 次に、正の引数の式に基づいて、 ゼータ[-1]は1 + 2 + 3 + 4 +の合計であると言えますが、 ゼータ[-1]を単純に計算できます。

これは信じられないほど奇妙な結果です。 しかし、一見しただけでは夢中になりません。 これは、現在、量子場の理論の特定の計算ではかなり合理的であると考えられている結果です(公平を期すために、現在のすべての無限大は最後にキャンセルされるように設計されています)。
話に戻りましょう。 ハーディとリトルウッドには、ラマヌジャンの受容可能な精神モデルがありませんでした。 リトルウッドは、ラマヌジャンが証拠を提供したくないと示唆した。なぜなら、彼は自分の研究を盗むのではないかと恐れていたからである(現在、窃盗は科学界で深刻な問題であった)。 ラマヌジャンは、これらの仮定によって「傷ついた」と言い、他の誰かが自分の方法を使うことを「少しでも恐れることはなかった」と保証した。 彼は、8年前にこの方法を発明したが、これまでのところ、それを評価できる人を見つけることができなかったと付け加えました。
同時に(ラマヌジャンの最初の手紙に答える前でも)、ハーディはインドの学生を担当する政府部門と一緒に、ラマヌジャンをケンブリッジに移す方法を研究していました。 彼らの通信のこのセグメントで何が起こったのかは完全には明らかではありませんが、ラマヌジャンは彼が行くことができないと答えました-おそらく彼のバラモンの信念のため、または彼の母親のため、またはおそらく彼は彼が新しい環境に適合します。 しかし、いずれにしても、ラマヌジャンの支持者は、彼がマドラス大学で奨学金を確実に受け取るようにしました。 他の専門家は、「 彼の結果は驚くべきものであるが、現時点では、それらの一部の明瞭な証拠を提供することはできない 」という見解を表明した。 同時に、「 彼は英語の十分な知識があり、本から現代の方法を学ぶには年を取りすぎていません 。」
大学の管理は、彼らの規則は、ラマヌジャンのように学士号を取得していない人に大学院奨学金を与えることを許可しないと述べました。 しかし、彼らは方法を提案しました:「登録法のセクションXVと1904年のインド大学法のセクション3は、州知事の同意を条件として、(国務省による)そのような奨学金の発行を可能にします。 評議会のジョージ 。」 そして、官僚制度にもかかわらず、事態は迅速に進み、数週間以内にラマヌジャンは四半期報告書を提出する唯一の要件で2年間の奨学金を正式に受け取りました。
ラマヌジャンのワークスタイル
, , . . , .
— , . . , .



, Mathematica . , . . , .
(, 1970- , , . 9. , — , — «9» «g». , , : " , 9 "!).
, . — , 16, 15.99999. , .
- , . , , :
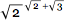
 。 . , (2,9755 ...) , (3,322 ...). - — , , , — - .
。 . , (2,9755 ...) , (3,322 ...). - — , , , — - .
, , , . Mathematica Wolfram Language , .
, , . . , , , .
, , — , , . , , . .
, . . , " ". , . .
. 1970- 1980- . . - , - : «» , . , , , , . — , , . , — , , . , ; .
, , , ( ) , , - . , , . 1910 Orders of Infinity — , ( , ; , , , Wolfram Language).
, « » , , , «» — .
,
- — , . , .
, 1914 " ", ( , ):

: " , , — ; ? " . ( "=" ≅):
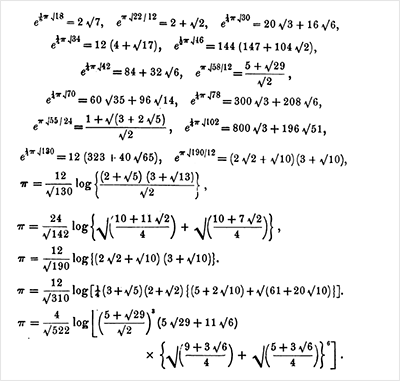
, ( ) :

«» ( 1706 ), 239:

: π . 1977 , 35 , . , — , Mathematica Wolfram Language.
, , , ( ) . , :

( ) « »:

確かにハーディにとって、ラマヌジャンの働き方は異質でした。 ラマヌジャンは数学の実験者でした。彼は自由に数学的可能性の世界に入り、興味深い重要な事実を見つけるために計算を行い、それからそれらに基づいて理論を構築しました。
一方、ハーディは伝統的な方法で働き、既存の数学の記述部分を徐々に拡大しました。 彼の作品のほとんどは、明示的または暗黙的に数学文書からのいくつかの結果の引用から始まり、その後、この結果がいくつかの正確なステップを使用してどのように配布されるかについての話を続けます。 彼は突然の経験的な発見も、直感に基づく不可解な飛躍もありません。 彼の数学は慎重に議論され、レンガごとに構築されています。
1世紀後、数学のほとんどすべての作業がこのように行われます。 そして、同じテーマが議論されたとしても、方法があまりにも異なるため、何かを「数学」と呼ぶべきではないでしょう。 私は自分で単純なプログラムの計算の世界を研究していましたが、たとえば数値に基づいた システム を研究しているという意味で、「数学」と呼ばれるものをかなりの量でやりました。
長年にわたり、私はあらゆる種類の興味深い結果を見つけてきました。 素数を生成する奇妙にネストされた再帰関係 。 XORツリー形式の整数の特異な表現 。 しかし、経験的事実だけでは、既存の数学の伝統の一部ではありません。
ハーディのような多くの数学者にとって、証明プロセスは数学的活動の基礎です。 真実を推測するのは簡単です。 他の数学者が理解できるように、何かが真実である理由を説明する証拠を作成することがより重要です。
今日、ますます多くの証拠を自動化できるようになると、このプロセスは手作業に似始めます。そこでは結果が興味深い場合がありますが、それを取得するプロセスはそうではありません。 しかし、証明プロセスも大いに役立ちます。 エビデンスは、この証明の詳細を超えた新しい抽象概念が導入される資料となり、他の多くの数学的結果を理解するための「原材料」にもなります。
これらの事実と結果が彼の数学的思考の中心であったラマヌジャンは、奇妙なヨーロッパの慣習のように感じ、特定の文脈から彼の結果を取り除き、ヨーロッパの数学者にそれらが真実であると納得させる必要があると思う。
ケンブリッジに行く
しかし、ラマヌジャンとハーディの話に戻ります。
1913年初頭までに、ハーディとラマヌジャンは手紙を交換し続けました。 ラマヌジャンは彼の結果を説明しました。 ハーディは彼を批判し、証拠とその伝統的な提示を主張した。 その後、長い休憩がありましたが、1913年12月、ハーディは再び、素数の分布に関するラマヌジャンの最も野心的な結果は間違いだったと書き、「 ...素数の理論には落とし穴がいっぱいで、その克服には現代の厳密な方法の適用が必要です」と書きました。 彼はまた、ラマヌジャンが自分の結果を証明できれば、「 数学の歴史の中で最も注目すべき数学的成果の1つ 」になると述べた。
1914年1月、ケンブリッジの若い数学者E. H.ネヴィルがマドラスに来て講義を行い、ハーディが「ラマヌジャンをケンブリッジに移そうとしている」と発表しました。 ラマヌジャンは1913年2月に、彼と彼の上司がマドラスの諮問学生委員会の秘書と会談し、彼はイギリスに行く準備ができているかどうか尋ねたと答えた。 ラマヌジャンは、イギリスに向けて出発する他のインド人学生と同じ方法で試験に合格するべきであると示唆し、彼はこれに対処できないと考え、彼の監督者は「 非常に正統的なバラモンであり、彼は外国に行く価値があるかどうか疑っていたので、彼は価値がないと言った 。」
彼は後に、ネヴィルは「疑念を払拭した」と述べ、費用を心配する必要はなく、彼の英語は誰にとっても幸せであり、試験を受ける必要がなく、イギリスで菜食主義者であり続けることができると説明した。 ラマヌジャンは、ハーディとリトルウッドが「 (イギリスで)数ヶ月間私を受け入れるのに苦労するのに十分親切 」になることを望んでいると言って結論を下しました。
ハーディは、官僚的な問題はなく、ラマヌジャンはイギリスに簡単に行くことを提案した。 しかし、そうではありませんでした。 ハーディが働いていたトリニティカレッジは、実際の資金を提供する準備ができていませんでした。 ハーディとリトルウッドはお金を提供しましたが、ネヴィルはマドラス大学の秘書に「 マドラス からの天才S.ラマヌジャンの発見は、数学の世界で私たちの時代の最も興味深い出来事であると約束しています 」と書いています。 ラマヌジャンの外国人サポーターは積極的な行動をとり、最終的にマドラス知事の注目を集めました。金は見つかりました。彼らは「休暇中に大学で講義を行う」ことを目的とした5年前の政府助成金から取られましたが、それは官僚の言葉でこのように聞こえました:教育省の文書No. 182「...」は、本来の目的に使用されていません。
官僚的なプロトコルに奇妙な追記がありました。たとえば、2月12日付けです。「どのカーストに属しますか? 早急に。」 しかし、結局、すべての困難は克服され、1914年3月17日、地元の高官の参加を得て見送った後、ラマヌジャンはイギリスに船に乗り、 スエズ運河を上り、 4月14日にロンドンに到着しました。 インドを離れる前、ラマヌジャンはヨーロッパでの生活の準備をしていました。彼は洋服を着て、ナイフとフォークで食事をし、ネクタイを結ぶことを学びました。 先にイングランドに来たインド人学生のために、全体の手順がありました。 数日後、ラマヌジャンがケンブリッジに到着し、インドの新聞は誇らしげに、「 高等数学の研究がケンブリッジで驚異的だったマドラスのラマヌジャン氏がトリニティの住居にいる」と報じた。
(ケンブリッジでのラマヌジャンの最初の日に関しては、ハーディとリトルウッドという名前に加えて、 ネヴィルとバーンズという2つの名前が表示されます。数学の一般的な歴史では特に知られていませんが、Wolfram言語ではそれらの名前にビルトイン機能があります: NevilleThetaSとBarnesG ) 。
ケンブリッジのラマヌジャン





ケンブリッジに到着したときのラマヌジャンはどんな感じでしたか? 彼は自信がありませんが、熱心で活動的であると言われています。 彼は時々彼の住所で冗談を言った。 彼は数学だけでなく、政治や哲学についても話すことができました。 彼はあまり反射的ではなかった。 コミュニケーションが公式であったとき、彼は礼儀正しく敬意を払い、現地の慣習に従おうとしました。 彼の母国語はタミル語で 、以前は英語の試験に失敗して失敗していましたが、イギリスに到着する頃には彼の英語は上手でした。 彼は他のインド人学生と一緒に遊んだり、時には音楽イベントに行ったり、川でボートをしたりするのが大好きでした。 彼は背が低くて満腹だった。 彼の主な注目すべき特徴は彼の目でした-明るく輝く。 彼は一生懸命働き、数学的問題を次々に解決した。 彼の貧弱な生活空間は、ほんの数冊の本と記事で構成されていました。 彼は実用的なことに賢明でした:例えば、料理の問題を解決したり、ベジタリアン製品を見つけたり。 ケンブリッジでは彼は幸せだったと言えます。
しかし、その後、1914年6月28日(ラマヌジャンがイギリスに到着してからわずか2ヶ月半)に、 フェルディナンド大公が殺され、7月28日に第一次世界大戦が始まりました。 これはすぐにケンブリッジに影響を与えました。 多くの学生が兵役に召集されました。 リトルウッドは軍に加わり、最終的に対空砲の射程表を計算する方法を開発しました。 ハーディは(特に彼がドイツの数学者を愛したという理由で)戦争の大きな支持者ではなかったが、彼はまた志願し、その後医学的理由で拒絶された。
ラマヌジャンは母親に手紙で戦争について説明しました。例えば、「 彼らは高高度で飛行機を飛ばし、都市を爆撃して破壊します。敵の飛行機が空に現れるとすぐに、地面に立つ飛行機が飛び立ち、高速で攻撃します」それは破壊と死をもたらします。 "
それにも関わらず、ラマヌジャンは数学の研究を続け、「 ラングーン が[マドラス]から遠く離れている限り遠く離れた領土で戦争が行われている」と母親に説明した。 また、実務上の困難もありました。たとえば、野菜が不足しているため、ラマヌジャンはインドからの友人に「 タマリンドの種と良質のココナッツ油 」を入れた小包を送るよう頼みました。 さらに重要なことは、ラマヌジャンが書いたように、「 ここの教授は、現在の戦争のために数学への関心を失っています 。」
また、ラマヌジャンは友人に「 結果を公表する計画を変更した 」と書いた。 彼は、彼の古い結果のいずれかを公表するために、戦争の終わりを待つと言いました。 しかし、彼はイギリスに到着してから「 彼らの方法 」を習得し、「 それらの方法で 新しい結果を得て、簡単に遅滞なく発行できるようにしようとした」 と述べた 。
1915年、ラマヌジャンは与えられた数の約数の数を数える関数(Wolfram言語のDivisorSigma )の最大値に関する「 高化合物 数 」と題する長い文書を発行しました。 ハーディは、おそらくこの記事の準備に積極的に参加し、ラマヌジャンの博士論文の論文の基礎になりました。
今後数年間、ラマヌジャンは実りある仕事をし、戦争にもかかわらず出版された記事を書きました。 Hardyと一緒に、彼は分布関数(Wolfram言語のPartitionsP )に関する重要な記事を書きました。これは、正の数の合計として整数を書く方法を説明しています。 この記事は、おおよその計算と正確な計算を混合する典型的な例です。 記事は、大きなnの結果で始まります。
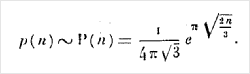
しかし、その後、インドで開発されたラマヌジャンのアイデアを使用して、得られた整数を取得できるポイントまでスコアが徐々に改善されます。 ラマヌジャンが住んでいた当時、 PartitionsP [200]の正確な値を計算することは大したことでした-そして彼の記事の集大成でした。 しかし、今日、ラマヌジャム法のおかげで、これらの計算は即座に実行できます。

ケンブリッジは戦争によって押しつぶされました-最前線で恐ろしいスピードで、より良い学生は死にました。 トリニティカレッジの大きな四角形は軍事病院になりました。 しかし、これにもかかわらず、ラマヌジャンは数学の研究を続けました-そして、ハーディの助けを借りて名声を得ました。
1917年5月、ラマヌジャンは病気になりました。 判断できる限り、おそらく彼はインドから持ち込まれた肝臓のある種の寄生虫感染でした。 しかし、だれも診断できませんでした。 ラマヌジャンは医者から医者に行きましたが、彼が言われたことを信じませんでした、そして、それは何も助けにならないように思われました。 数ヶ月で、彼は数学をするのに十分な気分になりました。 他では、いいえ。 彼は落ち込んで、ある時点で、どうやら、自殺しやすいようでした。 彼は、母親が妻をインドに返し、彼女とのコミュニケーションから保護し、彼女が彼の気を散らすことを恐れているという事実に助けられなかった。
ハーディは助けようとしました:時には医師と対話することによって、時には数学的なデータを提供することによって。 ある医師はハーディに、この病気の原因は「 現時点では完全に研究されていない東部からの未知の病原体 」かもしれないと語った 。 ハーディは、「 すべてのインディアンと同様に、ラマヌジャンは運命論者であるため、彼に自分の面倒を見てもらうことは非常に困難です。」 ハーディは後に病院でラマヌジャンを訪れた経緯について今や有名な話をし、タクシー番号1729で到着し、それはかなり退屈な番号だと思ったと言ったが、ラマヌジャンは答えた。 ;これは、2つの異なる方法で2つのキューブの合計として表現できる最小の数です :
 。 (Wolfram | Alpha は、その他のプロパティの一部もレポートするようになりました )。
。 (Wolfram | Alpha は、その他のプロパティの一部もレポートするようになりました )。
しかし、すべての問題にもかかわらず、数学者としてのラマヌジャンの評判は高まり続けました。 彼は王立協会の会員に選出され(ホブソンとベイカーを含み、誰も彼の元の手紙に応答しませんでした)、1918年10月に彼はトリニティカレッジの会員に選出されました。 第一次世界大戦が終わって1か月後、インドへの旅行を危険にさらした潜水艦攻撃の脅威はなくなりました。
そして1919年3月13日、ラマヌジャンはインドに戻りました-非常に有名で尊敬され、非常に病気です。 彼はまだ数学に従事しており、特にハーディに「誤った」シータ関数に関する注目すべき手紙を書いています( 1920年1月12日 )。 彼は謙虚に生きることを決心し、薬が彼にできることはほとんど無視した。 そして、1920年4月26日、32歳で、ノートに最後に入力してから3日後、彼は死にます。

次に起こったこと
ラマヌジャンが数学の勉強を始めたとき、彼は結果をハードカバーのノートに書き留め、それらのほんの一部だけを出版しました。 ラマヌジャンが亡くなったとき、ハーディは、ラマヌジャンのノートブックからの3,000件(またはそれ以上)の結果をすべて調査し、公開したかったのです。 1920年代および1930年代には数人の人々もこれに取り組み、その結果、多くのものが出版されました。 しかし、プロジェクトは完了していません-彼らは1970年代にのみそれに戻るでしょう。


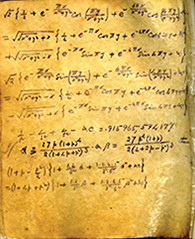



最初 、 2番目 、 3番目のノートブックをダウンロードします。
1940年、ハーディは自分が持っていたすべてのラマヌジャンの手紙をケンブリッジ大学の図書館に転送しましたが、ラマヌジャンが1913年に送った元の手紙はその中になかったので、現在私たちが持っているのはこの手紙のハーディへのその後の転写 。 ラマヌジャンの3つの主要なノートブックは、マドラス大学の司書のオフィスのキャビネットに長年置かれていました。そこでは昆虫に苦しみましたが、失われませんでした。 彼の他のメモはいくつかの手を通り抜け、それらのいくつかはケンブリッジの数学者の信じられないほど汚いオフィスに行き着いた 。 しかし、1965年に彼が亡くなったとき、彼らは発見され、図書館に送られ、1976年にラマヌジャンの記録が失われた「再発見」されるまで、彼らは塵を集めました。
ラマヌジャンが亡くなったとき、彼の親relativeはすぐに財政的支援を求め始めました。 治療のための大きな法案はイギリスから来ました、そして、お金を集めるためにラマヌジャンの論文を売ることについて話が始まりました。
ラマヌジャンの妻は、彼が亡くなったとき21歳でしたが、彼女はもはや結婚していませんでした。 彼女は非常に謙虚に暮らし、縫製によって生計を立てていました。 1950年に、彼女は亡くなった友人の息子の育成を引き受けました。 1960年代までに ラマヌジャンはインドのヒーローのようになり、さまざまな賞や年金を受け取り始めました。 何年もの間、多くの数学者が彼女を訪ねてきました。彼女の一人はラマヌジャンのパスポートから写真を渡しました。
彼女は長生きし、1994年に95歳で亡くなり、ラマヌジャンを73年間長生きしました。
ハーディはどうなりましたか?
ハーディはラマヌジャンの手紙を受け取ったとき35歳であり、彼が亡くなったとき43歳でした。 ハーディはラマヌジャンの「発見」を彼の最大の成果と見なし、彼らのコラボレーションを「 彼の人生で最初のロマンチックなイベント 」と表現しました。 ラマヌジャンの死後、ハーディはしばらくの間働き、結果の解読と開発を続けましたが、大部分は以前の数学的軌跡に戻りました。 彼の作品の完全なコレクションは、7つの大きなボリュームで構成されています(一方、ラマヌジャンの出版物は1つの薄い本です)。 彼の作品の名前からのこれらの雲は、発生した変更の一部のみを示しています(最初の雲-ラマヌジャンと会う前、2番目の雲-後):


ラマヌジャンが彼の人生に入った少し前に、ハーディはジョン・リトルウッドと協力し始めました(彼は後でリトルウッドがラマヌジャンよりも彼の人生にさらに影響を与えたと言うでしょう)。 ラマヌジャンが亡くなった後、ハーディはオックスフォードに移って仕事をし、ケンブリッジに戻る前に11年間住んでいた。 彼の不在は、たとえ彼らの部屋が数百フィートしか離れていなくても、主に書面によるメッセージングを通じて働いていたため、リトルウッドとのコラボレーションには影響しませんでした。 1911年以降、ハーディは共著者なしで出版されました。 最も実りの多いことに、彼はリトルウッドと仕事をし、38年以上に渡って95の記事を共著で出版しました。
ハーディの数学は常に最高の品質でした。 彼はリーマン仮説の解に似たものを作成することを夢見ていたが、実際には本当に壮観なことは何もしなかった。 彼は今日まで読まれている2冊の本を書きました: EMとの 「数論入門」 ライト リトルウッドとD.ポイアとの「不平等」 。
ハーディは知的エリートの間で彼の人生を生きました。 1920年代、彼は彼のアパートにレーニンのイメージを掲げ 、「科学労働者」組合の会長を短時間務めました。 : , . . , ( , ).
1940 . 12, . , . , . , — , , — , , " , - , " ( , - , ). , , .


, , , . , , " … ". , " 30 , , ". , , 1970- , — .


これは本当にそうですか? . , ( Wolfram|Alpha Wolfram Language) , . ( 40, , , ), , , 30 .

, . , , . , , . , . , , , . , , — . , , , , . , . , , , , .
, ( ) , , , , .
. , , , . 1947 70 .
, , 1977 . , , . , , , - , . , 72 , 80, , — .
? — . - , , , . , , « », ( Zentralblatt ):
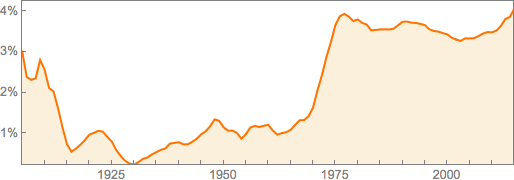
1900- . (, , ). 1930- . , .
1970- , ( , , , ).
1970- , , , , , . 1982 , , ( , - ):

1970- ( , ), . , .
- . (-, , - ..) «». ; , «», , .
, , Mathematica Wolfram Language , RamanujanTau , RamanujanTauL , RamanujanTauTheta RamanujanTauZ . , . , « -» ( , ).
- , ( «24»):
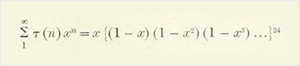
, — , - , .
— ?
, 1 + 2 + 3 + 4 = 10. , , . , . ( ) , . — , .
, , , . , . . , , , , . , , — .
. , , , .
? , . -, , , , , , . , , , , , .
, ; , . , . . . , , , - . 1931 ( , , -, ) , -: , .
1960- . , , ( ) , . . , , , , . , , , . , , , (, ).
, , . . .
, , , . , ; , .
, , , «» , .
, , . , , , - . , .
, , . , , , , .
, , . : ?
, . , . , , . , « ». .
, , . , , , ( - ) «» .
, . , , : . , . ( ), .
, , , ? , . , , , - .
, « »: , , . — . : .
, , , . , . , — , .
?
- ? , , , , 30 , — , 1913 . , , ( ) , ,
 。
。

? … Wolfram|Alpha , , .

. , . AI . , , : - , , . ; . ( ) - , «», .
, «» , . , . , ( ), . , , .
, , , . . - , . , , , , , .
. , , , . , . , , , — , , .
« »: , , , . , , Mathematica Wolfram Language . , : , , . , , .
, : . , , , , , - ( ) .
, , ( ).
, - , . , . , , , (, , ), . - Wolfram Language . , - , , .
, . (. " Wolfram: " ) - . ( ) , . , — . , - 14- , , , …
, Mathematica?
— , — . (Mathematica Wolfram Language), ( ).
, . , , , , , , .
. , , , : , .
, , . — , . , , , — .