弾性構造は、データを近似するための最も一般的なタイプの構造です。 これはノードとそれらの間の弾性結合のセットです。 このような接続は、ポイント間の平衡距離を持つ一対のポイント間のスプリング接続、およびノード間の平衡角度を持つトリプルのノードの補強材にすることができます。 弾性構造によってポイントのセットを近似するには、弾性構造のノードを引き付ける中心としてデータポイントの物理的解釈を使用することを提案します。 弾性構造の特殊なケースは、非線形主成分です。 これは、共通の交点を持つ弾性チェーンのセットです。 弾性結合の高い剛性により、非線形主成分は因子分析の古典的な主成分に変換されます。 引力場における弾性構造の点の動きを計算し、弾性構造のノード間の結合を考慮するために、Verlet数値積分法を使用することが提案されています。
多次元スケーリングにより、ターゲット空間の次元の仮説の枠組み内で、オブジェクト間の再構築された距離が経験に近いように、相互距離に従ってオブジェクトを配置することができます。 Verlet法に基づいて、多次元スケーリングを実行することが提案されています。これにより、ポイント間の相互距離が最も正確に考慮されます。 相互距離のマトリックスが相関マトリックスになります。 多次元スケーリングを使用して、相関行列の因数分解が実行され、それにより、因子空間のデータの因子構造が復元されます。 解釈可能な解を得るために、再構築された要因構造に適用される要因回転の個別の方法を使用することが提案されています。
1. Verletメソッド
Verletアルゴリズムを使用して、現在および過去から次の点の位置を計算します。
、
-i番目の反復でj番目の点の計算された座標、
mは空間の次元、
j番目の点の速度ベクトルです。
データ点で表されるk番目の引力中心の影響ベクトル 
、 j番目のポイントまで、
。
ポイントシステムには制限が課せられます。一部のポイントは、所定の長さの弾性ロッドで接続されています。
アルゴリズムは次のように機能します。
- 1.ポイントの新しい位置が計算されます。
- 2.接続ごとに、対応する条件が満たされます。
- 3.ステップ2をs回繰り返します。
たとえば、 s = 16。
結合緩和手順は、次の式で説明されます。
関係がドットで表されている場合
そして 
それらの間の平衡距離で 
それから
、
、
、
-結合弾性係数、
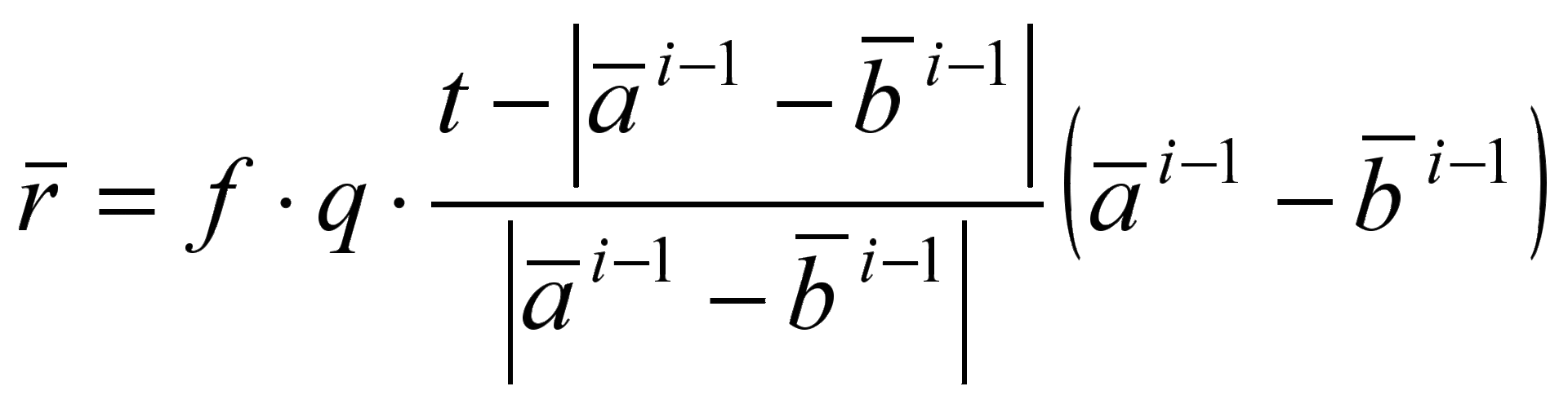ステップ2 の繰り返し回数sに依存する係数です。
図 1.平衡距離を持つ一対の点のバネ接続
トリプルノードは、平衡角を持つスティフナーを形成できます。 極点間の弾性棒の形の結合により、そのような結合をエミュレートすることが提案されています。 この場合の極値間の平衡距離は、三角形の等値から設定されます。 関係がドットで表されている場合
、 、 
平衡角あり 
平衡距離 
次の式で計算されます：
。
図 2.平衡角をもつ三重点の補剛材
2.多次元スケーリング
多次元スケーリング（MNS）は、オブジェクト間で観測される距離をほぼ維持する、オブジェクトの最も効率的な配置の方法です。 MNSは、指定された次元の空間にオブジェクトを配置し、結果の構成がオブジェクト間の距離をどれだけ正確に保存するかをチェックします。 MNSはアルゴリズムを使用して、結果の表示オプションの品質を評価する関数を最小化します。
類似性の元のマトリックスの再現の程度によって測定されるモデル（ディスプレイ）のフィッティングの品質を評価するために最も頻繁に使用される尺度は、いわゆるストレスです。 現在の構成の応力値φは、次のように決定されます。
。
ここで、 d ijは、与えられた次元の空間で再現された距離です。
δijは初期距離です。
mはオブジェクトの数です。
関数f（ δij ）は、ソースデータ（距離）の非計量単調変換を示します。 MNSは、オブジェクトの類似性の定量的尺度ではなく、相対的な順序のみを再現します。 応力値が低いほど、初期距離行列は結果の距離行列と一致します。
3.主なコンポーネントと因子モデル
主要コンポーネントのモデルは、次の式で説明されます。
mは変数の数、
gは因子の数です
-ソース変数、
-一般的な要因
-特定の要因。
4.弾性因子構造
Verletメソッドのポイントシステムとして、軸で表される座標系を使用できます。
、
どこで
wは因子軸を形成する点の数です。
、
gは因子軸の数です。
たとえば、
（数wは1より大きい奇数でなければなりません）
lは、因子軸を形成する一対の隣接点間の距離です。
-因子軸の中心点のインデックス。
ポイントペア
平衡距離lとの接続を形成します。
ポイントペア
平衡距離との関係を形成する 
。
すべてのポイントのペア
異なる軸iとjは、平衡距離がゼロの関係を形成します。
ポイントペア
、 
、 
、 
異なる軸iとjは、ポイント間の初期距離に等しい平衡距離との関係を形成します。 これらの関係は、異なる因子軸iとjの間の直角を定義します。 直交因子構造を指定する別の方法は、点のトリプル間で直接平衡角を持つスティフナーを追加することです 
異なる階乗軸iとjの間 。
図 3. Verletメソッドの因子構造を指定する方法
因子構造の要素
は、元の座標系のj番目の因子軸とi番目の軸の間の相関係数として定義できます。
、
、
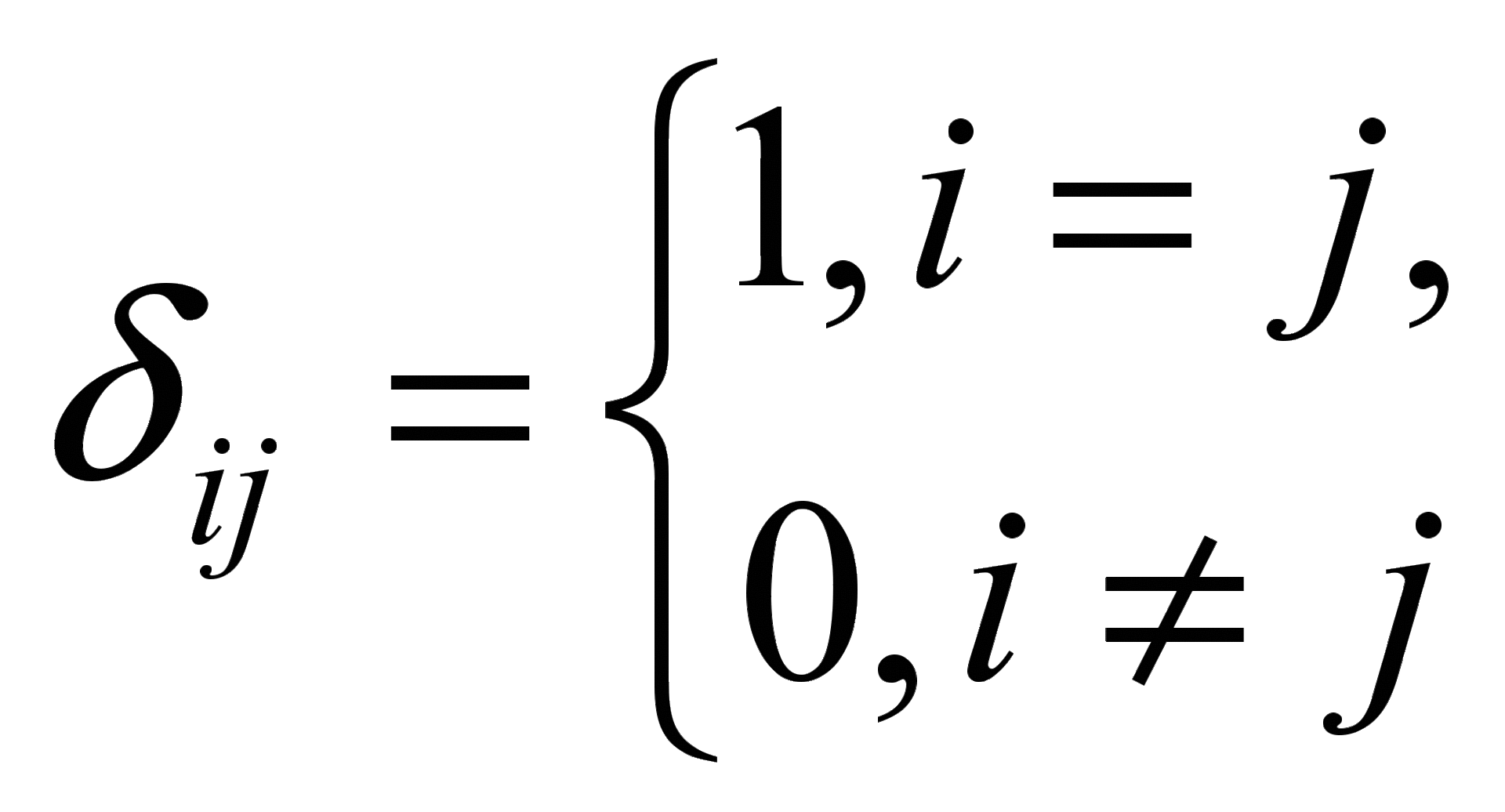-クロネッカーのシンボル、
j番目の因子軸の方向ベクトルです。
5.多次元スケーリングの弾性構造
初期変数間の相関は、正規化された後者とゼロ平均と単位分散のスカラー積として定義できます。
nは、元の変数空間の次元です。
初期変数間の相関係数は、多次元尺度法の相互距離のマトリックスと同様の相関マトリックスを決定します。 因子空間内の近くのオブジェクトは相関係数の大きな値に対応するため、相互距離の行列の要素d ijは、式に従って相関行列r ijの対応する要素から取得されます。
。
Verletメソッドを使用すると、因子構造は因子空間の次元gの仮説の枠組み内で復元されます。
因子構造の要素
j番目の因子軸とi番目の変数の間の相関係数として定義できます。
、
、
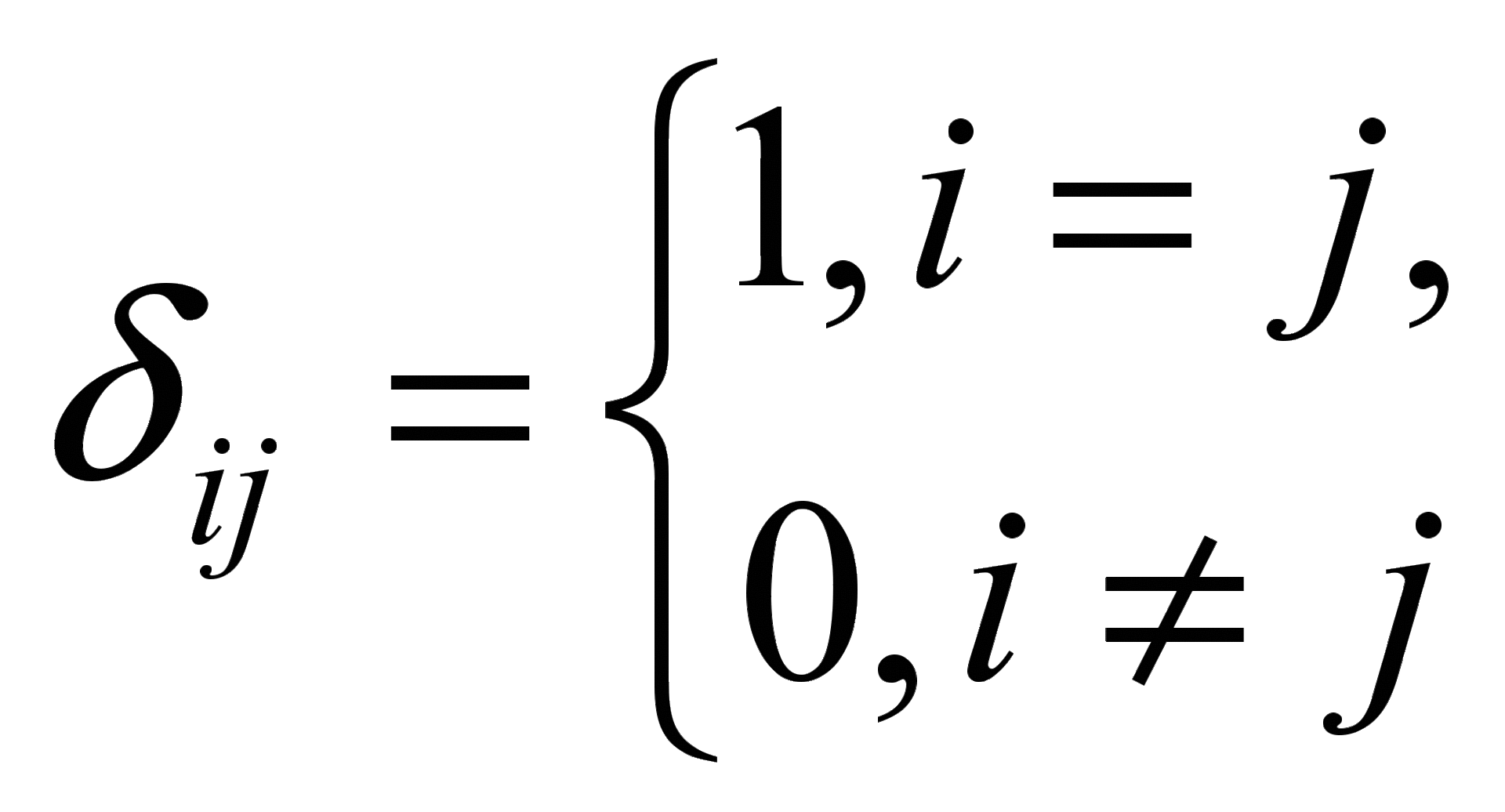-クロネッカーのシンボル、
因子空間のj番目の変数の方向ベクトルです。
因子空間のj番目の変数です。
-因子空間の変数の因子構造の重心。
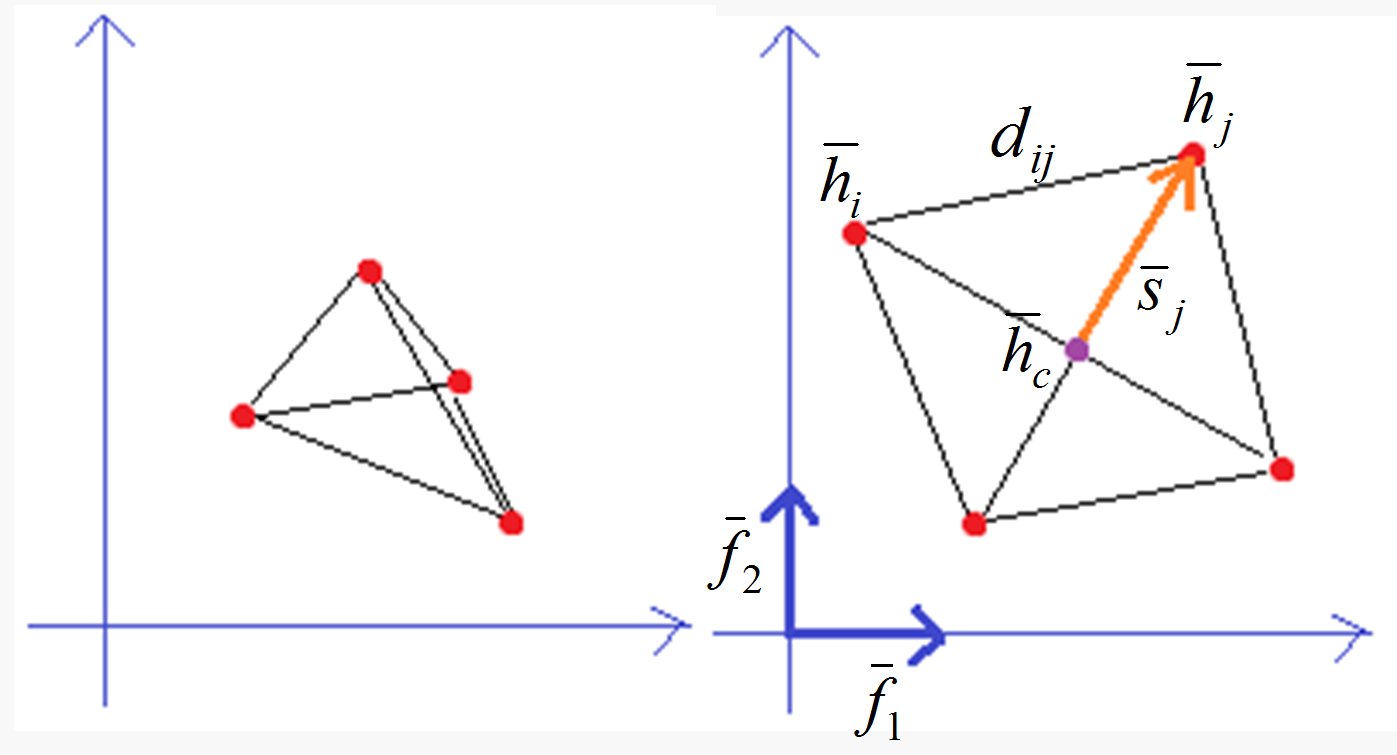
図 4.多次元スケーリングの弾性構造
6.ソフトウェアの実装
Verletメソッドは、パブリックJavaScriptライブラリVerlet.jsを使用してプログラムで実装され、多次元の場合に改善されました。 Verlet法に基づく弾性因子構造と多次元スケーリングの計算方法による因子分析のWebアプリケーションは、新しいユーザーを登録した後、 http：//svlaboratory.org/application/pcaおよびhttp://svlaboratory.org/application/multscalで入手できます。 このアプリケーションを使用すると、特定の座標平面でVerletメソッドの収束プロセスを視覚化できます（図5）。
図 5. WebアプリケーションでのVerletメソッドの視覚化
7.数値実験
初期パラメータとして、初期の動脈性高血圧症の131人に対して15の生物物理学的指標が採用されました。
1）重量
2）ボディマスインデックス（BMI）、
3）呼吸数（BH）、
4）好中球のセグメント化（C）、
5）リンパ球（L）、
6）左心室の収縮終期サイズ（DAC）、
7）左心室の収縮末期容積（CSR）、
8）左心室の拡張末期サイズ（CBC）、
9）左心室の拡張末期容積（BWW）、
10）衝撃量（UO）、
11）心拍出量（MOS）、
12）総末梢血管抵抗（OPSS）、
13）ヒルデブラント指数（THEM）、
14）左心室の駆出率（EF）、
15）左心室（FU）の短縮の割合。
これらの高血圧の結果として生じる因子構造を表1、2、3に示します。
表1.初期階乗解（弾性階乗構造のVerlet法）
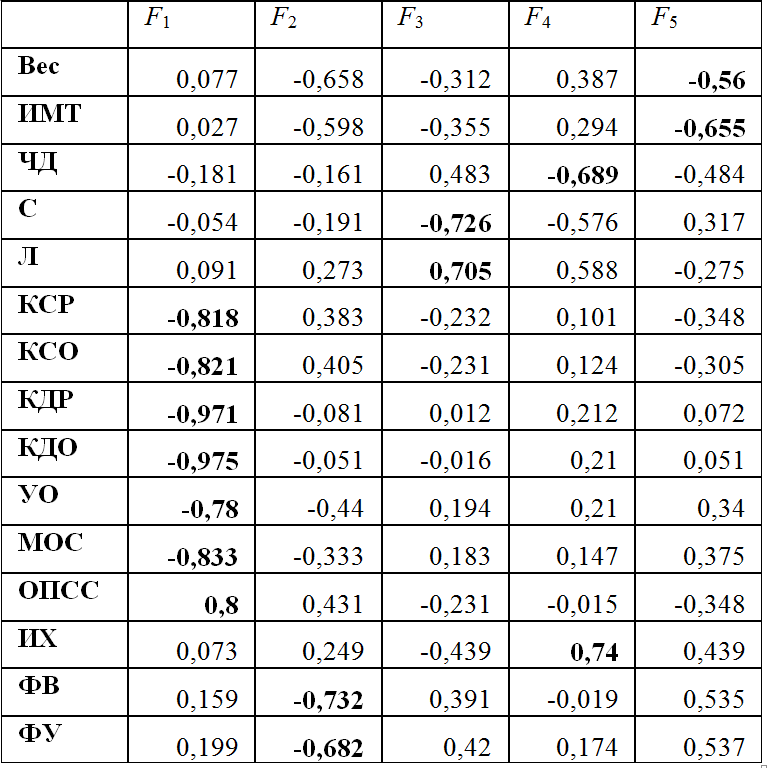
表2.初期の階乗解（多次元スケーリングのVerlet法）
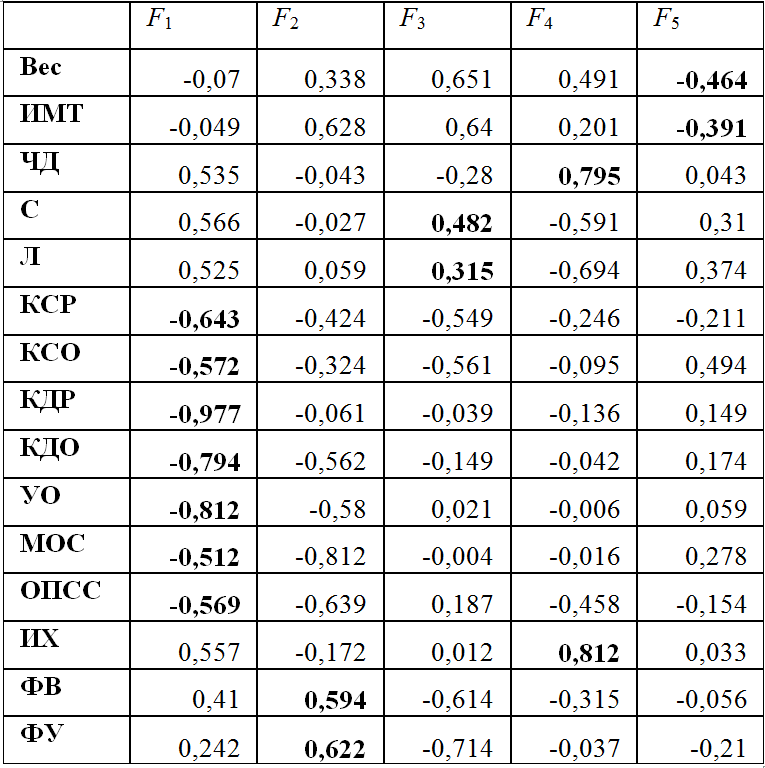
表3.初期の階乗解（固有ベクトル法）
[1]で提案された解釈可能性基準による因子回転後の因子解を表4、5、6に示します。これらの因子構造は、以前の研究[2、3]で確認されています。
表4.解釈可能性の基準による因子構造（弾性因子構造のVerlet法）
表5.解釈可能性の基準による因子構造（多次元スケーリングのVerlet法）
表6.解釈可能性の基準による因子構造（固有ベクトル法）
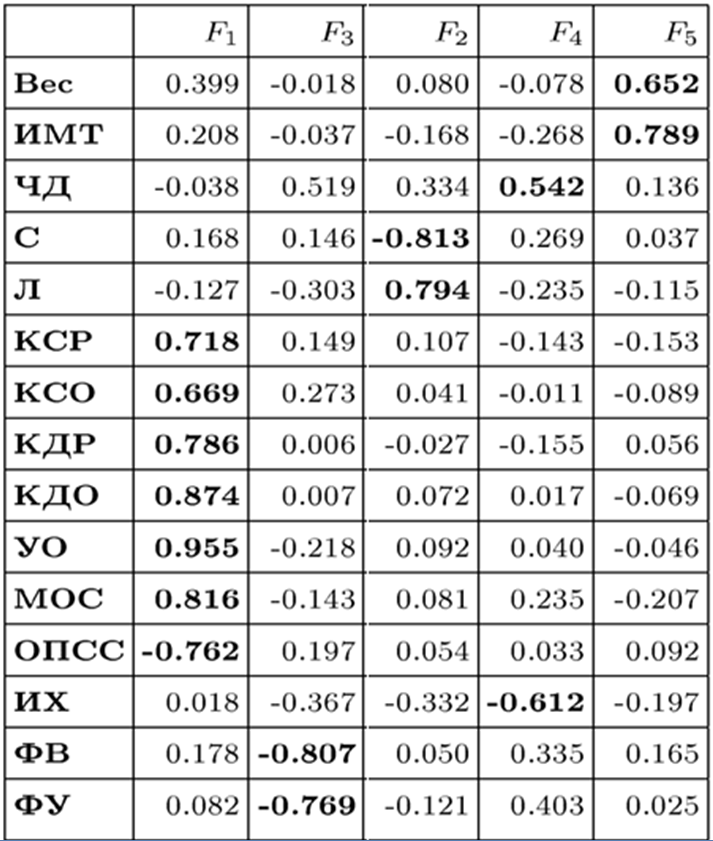
おわりに
弾性構造として、因子軸と因子軸の異なるポイント間の関係を含む多次元因子構造が使用されました。 Verlet法と引力の中心としての多次元空間のデータポイントの物理的解釈を使用して、弾性構造によってポイントのセットを近似しました。 相関行列に適用されるVerlet法に基づく多変量スケーリング法は、代替の因数分解法です。 任意の構造を多次元弾性構造として使用できるため、提案されたVerlet法に基づく近似法は一般化された特性を持ちます。
初期高血圧の15の生物物理学的指標について、Verlet法に基づく因子構造が得られました。 得られた因子構造は、古典的な固有ベクトル法とよく相関しており、以前の研究の結果によっても確認されています。
参照資料
- 1. Shovin V. A.、Goltyapin V. V.因子構造の回転方法//数学的構造とモデリング-2015. No. 2（34）。 S. 75-84。
- 2. Goltyapin V.V.、Shovin V.A. 第一段階の動脈高血圧の斜め要因モデル。 //オムスク大学の会報。 2010. No. 4. c。 120-128。
- 3. Shovin V.A. 動脈性高血圧の確認的要因モデル。 //コンピューターの調査とモデリング。 2012. T. 4. No. 4. c。 885-894。