先日、次の世界ホッケー選手権が終了しました。
試合を見ながら、アイデアが生まれました。 休憩中にテレビカメラがロッカールームに向かっているプレーヤーを示すとき、彼らがどれほど巨大であるかに気付かないのは難しいです。 コーチ、チームの機能、アイスアリーナの従業員、ジャーナリストまたはファンだけを背景に、彼らは通常非常に印象的に見えます。
そして、私は疑問に思いました。 ホッケー選手は普通の人より上ですか? ホッケー選手の成長は、一般の人々と比べて時間とともにどのように変化しますか? 永続的なクロスカントリーの違いはありますか?
データ
世界のホッケー選手権を主催する組織であるIIHFは、毎年、参加選手のラインナップと各選手の身長と体重に関する情報を公開しています。 このデータのアーカイブはこちらです。
2001年から2016年までのすべての世界選手権のデータを集めました。 年々、データを提供するための形式はわずかに変更されており、データをクリーンアップするには多少の努力が必要です。 プロセスを正しく自動化する方法を想像することなく、すべてのデータを手動でコピーしました。これには3時間強かかりました。 結合されたデータセットは公開されています。
# load required packages require(dplyr) # data manipulation require(lubridate) # easy manipulations with dates require(ggplot2) # visualization require(ggthemes) # themes for ggplot2 require(cowplot) # nice alignment of the ggplots require(RColorBrewer) # generate color palettes require(texreg) # easy export of regression tables require(xtable) # export a data frame into an html table # download the IIHF data set; if there are some problems, you can download manually # using the stable URL (https://dx.doi.org/10.6084/m9.figshare.3394735.v2) df <- read.csv('https://ndownloader.figshare.com/files/5303173') # color palette brbg11 <- brewer.pal(11,'BrBG')
ホッケー選手は成長していますか? 大まかな(定期的な)比較
そもそも、16の全世界選手権でのプレーヤーの平均成長率を比較します。

# mean height by championship df_per <- df %>% group_by(year) %>% summarise(height=mean(height)) gg_period_mean <- ggplot(df_per, aes(x=year,y=height))+ geom_point(size=3,color=brbg11[9])+ stat_smooth(method='lm',size=1,color=brbg11[11])+ ylab('height, cm')+ xlab('year of competition')+ scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+ theme_few(base_size = 15)+ theme(panel.grid=element_line(colour = 'grey75',size=.25)) gg_period_jitter <- ggplot(df, aes(x=year,y=height))+ geom_jitter(size=2,color=brbg11[9],alpha=.25,width = .75)+ stat_smooth(method='lm',size=1,se=F,color=brbg11[11])+ ylab('height, cm')+ xlab('year of competition')+ scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+ theme_few(base_size = 15)+ theme(panel.grid=element_line(colour = 'grey75',size=.25)) gg_period <- plot_grid(gg_period_mean,gg_period_jitter)
前向きな傾向は明らかです。 10年半にわたって、ワールドカップでのホッケー選手の平均成長は、ほぼ2センチメートル増加しました(左のパネル)。 かなり大きなバリエーションを背景にわずかに増加するように(右パネル)。 それはたくさんですか、それとも少しですか? 質問に答えるには、母集団と正しく比較する必要があります(ただし、これについては記事の最後で詳しく説明します)。
コホート分析
成長の変化を研究するより正確な方法には、出生コホートの比較が含まれます。 ここで私たちは奇妙なニュアンスに直面しています-一部のホッケー選手は複数の世界選手権に参加しました。 質問:同じ人の重複した録音を削除しますか? チャンピオンシップでのホッケー選手の平均的な成長に興味がある場合(上の写真のように)、クリアすることはおそらく意味がありません。 しかし、ホッケー選手の成長の変化を追跡したい場合、私の意見では、定期的に世界選手権に出場した選手により多くのウェイトを割り当てるのは間違っているでしょう。 したがって、さらに分析するために、同じプレーヤーの繰り返しのエントリからデータを消去しました。
# remove double counts dfu_h <- df %>% select(year,name,country,position,birth,cohort,height) %>% spread(year,height) dfu_h$av.height <- apply(dfu_h[,6:21],1,mean,na.rm=T) dfu_h$times_participated <- apply(!is.na(dfu_h[,6:21]),1,sum) dfu_w <- df %>% select(year,name,country,position,birth,cohort,weight) %>% spread(year,weight) dfu_w$av.weight <- apply(dfu_w[,6:21],1,mean,na.rm=T) dfu <- left_join(dfu_h %>% select(name,country,position,birth,cohort,av.height,times_participated), dfu_w %>% select(name,country,position,birth,cohort,av.weight), by = c('name','country','position','birth','cohort')) %>% mutate(bmi = av.weight/(av.height/100)^2)
観測の総数は6292から3333に減少しました。ホッケー選手が複数の世界選手権に参加した場合、個々のホッケー選手の身長と(特に)体重は時間とともに変化する可能性があるため、身長と体重のデータを平均しました。 ホッケー選手は、世界選手権でナショナルチームのプレーの名誉を何回獲得しますか? 平均して2倍弱。
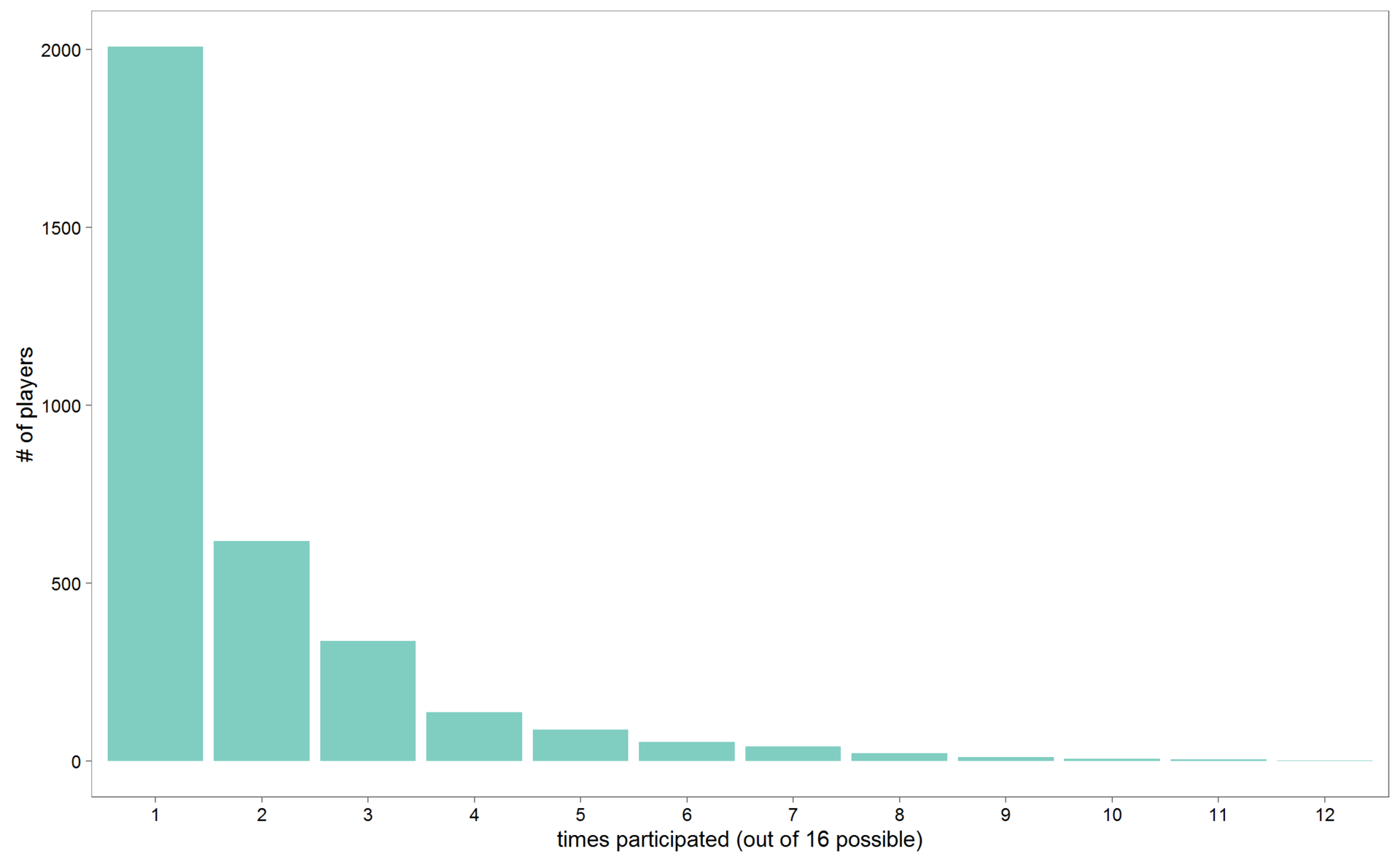
# frequencies of participation in world championships mean(dfu$times_participated) df_part <- as.data.frame(table(dfu$times_participated)) gg_times_part <- ggplot(df_part,aes(y=Freq,x=Var1))+ geom_bar(stat='identity',fill=brbg11[9])+ ylab('# of players')+ xlab('times participated (out of 16 possible)')+ theme_few(base_size = 15)
しかし、ユニークなものがあります。 少なくとも10の世界選手権に参加したプレーヤーを見てみましょう。 そのようなプレーヤーは14人いました。
# the leaders of participation in world championships # save the table to html leaders <- dfu %>% filter(times_participated > 9) View(leaders) print(xtable(leaders), type="html", file="table_leaders.html")
| お名前 | 国 | 位置 | 誕生 | コホート | 身長 | times_participated | 平均重量 | BMI | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | オベチキン・アレキサンダー | RUS | F | 1985-09-17 | 1985 | 188.45 | 11 | 98.36 | 27.70 |
| 2 | ニールセン・ダニエル | デン | D | 1980-10-31 | 1980 | 182.27 | 11 | 79.73 | 24.00 |
| 3 | スタール・キム | デン | F | 1978-03-10 | 1978 | 182.00 | 10 | 87.80 | 26.51 |
| 4 | グリーンモーテン | デン | F | 1981-03-19 | 1981 | 183.00 | 12 | 85.83 | 25.63 |
| 5 | マサルスキエドガーズ | ラット | G | 1980-03-31 | 1980 | 176.00 | 12 | 79.17 | 25.56 |
| 6 | アンブール・アンドレス | すい | F | 1983-09-14 | 1983 | 176.80 | 10 | 83.70 | 26.78 |
| 7 | グラナク・ドミニク | SVK | D | 1983-06-11 | 1983 | 182.00 | 10 | 79.50 | 24.00 |
| 8 | マッドセン・モーテン | デン | F | 1987-01-16 | 1987 | 189.82 | 11 | 86.00 | 23.87 |
| 9 | レッドリー・ミケリス | ラット | F | 1984-07-01 | 1984 | 180.00 | 10 | 80.40 | 24.81 |
| 10 | Cipulis Martinins | ラット | F | 1980-11-29 | 1980 | 180.70 | 10 | 82.10 | 25.14 |
| 11 | ホロス・ジョナス | また | D | 1987-08-27 | 1987 | 180.18 | 11 | 91.36 | 28.14 |
| 12 | バスティアンセン・アンダース | また | F | 1980-10-31 | 1980 | 190.00 | 11 | 93.64 | 25.94 |
| 13 | モルテンに尋ねる | また | F | 1980-05-14 | 1980 | 185.00 | 10 | 88.30 | 25.80 |
| 14 | フォルスバーグ・クリスチャン | また | F | 1986-05-05 | 1986 | 184.50 | 10 | 87.50 | 25.70 |
アレクサンダーオベチキン、11回! しかし、ここでは、原則として、すべてのホッケープレーヤーが16のすべてのチャンピオンシップに参加することは不可能であったことに注意する必要があります。 3)そして、プレーヤーが代表チームに安定して入ったかどうか。 最後に、NHLが、世界選手権への参加から最高のベストを安定的にそらします。

# countries times participated df_cnt_part <- df %>% select(year,country,no) %>% mutate(country=factor(paste(country))) %>% group_by(country,year) %>% summarise(value=sum(as.numeric(no))) %>% mutate(value=1) %>% ungroup() %>% mutate(country=factor(country, levels = rev(levels(country))), year=factor(year)) d_cnt_n <- df_cnt_part %>% group_by(country) %>% summarise(n=sum(value)) gg_cnt_part <- ggplot(data = df_cnt_part, aes(x=year,y=country))+ geom_point(color=brbg11[11],size=7)+ geom_text(data=d_cnt_n,aes(y=country,x=17.5,label=n,color=n),size=7,fontface=2)+ geom_text(data=d_cnt_n,aes(y=country,x=18.5,label=' '),size=7)+ scale_color_gradientn(colours = brbg11[7:11])+ xlab(NULL)+ ylab(NULL)+ theme_bw(base_size = 25)+ theme(legend.position='none', axis.text.x = element_text(angle = 90, hjust = 1,vjust=0.5))
ホッケー選手は成長していますか? 回帰分析
回帰分析を使用すると、プレーヤーの成長の変化に関する質問により正確に答えることができます。 この場合、多項線形回帰を使用して、出生コホートに応じてホッケー選手の成長が予測されます。 回帰モデルの仕様にさまざまな追加(制御)変数を含めると、最も興味深い係数「セテリスパリバス」の値が得られます。 たとえば、説明変数に加えて、出生コホート、フィールドでのプレイヤーの位置に加えて、成長とコホートの関係を取得し、位置による違いの影響をクリアします。 国の制御変数に追加すると、結果が得られ、国間の違いが解消されます。 もちろん、制御変数自体が重要な場合、これも注意する価値があります。
回帰モデル(特に線形回帰)は、外れ値に非常に敏感です(たとえば、 この記事を参照 )。 この広範なトピックに深く入ることなく、代表者が少なすぎるコホートを分析から削除しました。
# remove small cohorts table(dfu$cohort) dfuc <- dfu %>% filter(cohort<1997,cohort>1963)
データをあまりカットしたくないので、プレイヤーが10人未満の1963年、1997年、1998年のコホートのみを削除しました。
だから、回帰分析の結果。 次の各モデルでは、1つの変数を追加します。
従属変数 :ホッケー選手の成長。
説明変数 :1)出生コホート。 2)+フィールド上の位置(ディフェンダーとの比較); 3)+国(ロシアとの比較)。
# relevel counrty variable to compare with Russia dfuc$country <- relevel(dfuc$country,ref = 'RUS') # regression models m1 <- lm(data = dfuc,av.height~cohort) m2 <- lm(data = dfuc,av.height~cohort+position) m3 <- lm(data = dfuc,av.height~cohort+position+country) # export the models to html htmlreg(list(m1,m2,m3),file = 'models_height.html',single.row = T)
| モデル1 | モデル2 | モデル3 | ||
|---|---|---|---|---|
| (傍受) | -10.17(27.67) | -18.64(27.01) | 32.59(27.00) | |
| コホート | 0.10(0.01) *** | 0.10(0.01) *** | 0.08(0.01) *** | |
| positionF | -2.59(0.20) *** | -2.59(0.20) *** | ||
| 位置G | -1.96(0.31) *** | -1.93(0.30) *** | ||
| countryAUT | -0.94(0.55) | |||
| countryBLR | -0.95(0.53) | |||
| countryCAN | 1.13(0.46) * | |||
| countryCZE | 0.56(0.49) | |||
| 国DEN | -0.10(0.56) | |||
| countryFIN | 0.20(0.50) | |||
| countryFRA | -2.19(0.69) ** | |||
| countryGER | -0.61(0.51) | |||
| countryHUN | -0.61(0.86) | |||
| countryITA | -3.58(0.61) *** | |||
| countryJPN | -5.24(0.71) *** | |||
| 国KAZ | -1.16(0.57) * | |||
| countryLAT | -1.38(0.55) * | |||
| countryNOR | -1.61(0.62) ** | |||
| countryPOL | 0.06(1.12) | |||
| countrySLO | -1.55(0.58) ** | |||
| countrySUI | -1.80(0.53) *** | |||
| countrySVK | 1.44(0.50) ** | |||
| countrySWE | 1.18(0.48) * | |||
| countryUKR | -1.82(0.59) ** | |||
| 国USA | 0.54(0.45) | |||
| R 2 | 0.01 | 0.06 | 0.13 | |
| 調整 R 2 | 0.01 | 0.06 | 0.12 | |
| 数 obs。 | 3319 | 3319 | 3319 | |
| Rmse | 5.40 | 5.27 | 5.10 | |
| *** p <0.001、 ** p <0.01、 * p <0.05 | ||||
モデルの解釈
モデル1 コホートの1年間の増加は、ホッケー選手の成長の0.1 cmの増加に対応します。係数は統計的に有意ですが、モデルは従属変数の変動の1%のみを説明します。 原則として、これは問題ではありません。シミュレーションは本質的に説明的であるため、予測のタスクは提示されません。 ただし、低い決定係数は、高さのホッケー選手間の違いをよりよく説明する他の変数があるべきであることを示します。
モデル2 ディフェンダーはホッケーの最高選手です。 ゴールキーパーは2 cm低く、攻撃者は2.6 cm低く、すべての確率は統計的に有意です。 説明されている従属変数の変動は6%に増加します。 この場合、可変出生コホートの係数は変化しません。
モデル3 。 国に制御変数を追加することは、2つの理由で興味があります。 まず、いくつかの違いは統計的に有意であり、それ自体が興味深いものです。 たとえば、スウェーデン人、スロバキア人、カナダ人は、私たちのプレーヤーよりも統計的に著しく高いです。 ほとんどの国は私たちよりはるかに低く、日本人は5.2 cm、イタリア人は3.6 cm、フランス人は2.2 cmです(図4も参照)。 第二に、国への制御変数の導入は、変数の出生コホートの係数を0.08に大幅に削減します。 これは、クロスカントリーの違いが出生コホートの違いの一部を説明することを意味します。 モデルの決定係数は13%に増加します。

# players' height by country gg_av.h_country <- ggplot(dfuc ,aes(x=factor(cohort),y=av.height))+ geom_point(color='grey50',alpha=.25)+ stat_summary(aes(group=country),geom='line',fun.y = mean,size=.5,color='grey50')+ stat_smooth(aes(group=country,color=country),geom='line',size=1)+ #geom_hline(yintercept = mean(height),color='red',size=.5)+ facet_wrap(~country,ncol=4)+ coord_cartesian(ylim = c(170,195))+ scale_x_discrete(labels=paste(seq(1965,1995,10)),breaks=paste(seq(1965,1995,10)))+ theme_few(base_size = 15)+ theme(legend.position='none', panel.grid=element_line(colour = 'grey75',size=.25))
最も完全なモデルは、ホッケー選手の成長が年間0.08 cmの割合で増加することを示しています。 これは、1964年から1996年までの32年間で10年ごとに0.8 cmまたは2.56 cm増加することを意味します。制御変数を考慮すると、ホッケー選手の成長率は平均値のより粗い分析よりも約1.5倍低いことに注意してください(図1): 10年ごとに0.8 cm対約1.2 cm。
成長の増加がどれほど重要であるかを最終的に理解しようとする前に、もう1つの興味深い点に注意を払いたいと思います。 制御変数の導入は、回帰直線の単一の勾配(主な説明変数の単一の係数)を使用してカテゴリ間の違いを修正することを意味します。 これは常に良いとは限らず、サブサンプルで調査された変数間の関係の緊密さの大きな違いを隠すことができます。 たとえば、プレーヤーの成長が役割に依存していることを示す別のシミュレーション(図5)は、関係がゴールキーパーで最も顕著であり、ディフェンダーで最も目立たないことを示しています。

dfuc_pos <- dfuc levels(dfuc_pos$position) <- c('Defenders','Forwards','Goalkeeprs') gg_pos <- ggplot(dfuc_pos ,aes(x=cohort,y=av.height))+ geom_jitter(aes(color=position),alpha=.5)+ stat_smooth(method = 'lm', se = T,color=brbg11[11],size=1)+ scale_x_continuous(labels=seq(1965,1995,5),breaks=seq(1965,1995,5))+ scale_color_manual(values = brbg11[c(8,4,10)])+ facet_wrap(~position,ncol=3)+ xlab('birth cohort')+ ylab('height, cm')+ theme_few(base_size = 20)+ theme(legend.position='none', panel.grid=element_line(colour = 'grey75',size=.25))
# separate models for positions m3d <- lm(data = dfuc %>% filter(position=='D'),av.height~cohort+country) m3f <- lm(data = dfuc %>% filter(position=='F'),av.height~cohort+country) m3g <- lm(data = dfuc %>% filter(position=='G'),av.height~cohort+country) htmlreg(list(m3d,m3f,m3g),file = '2016/160500 Hockey players/models_height_pos.html',single.row = T, custom.model.names = c('Model 3 D','Model 3 F','Model 3 G'))
| モデル3 D | モデル3 F | モデル3 G | ||
|---|---|---|---|---|
| (傍受) | 108.45(46.46) * | 49.32(36.73) | -295.76(74.61) *** | |
| コホート | 0.04(0.02) | 0.07(0.02) *** | 0.24(0.04) *** | |
| countryAUT | 0.14(0.96) | -2.01(0.75) ** | 0.47(1.47) | |
| countryBLR | 0.30(0.87) | -1.53(0.73) * | -2.73(1.55) | |
| countryCAN | 1.55(0.78) * | 0.39(0.62) | 3.45(1.26) ** | |
| countryCZE | 0.87(0.84) | 0.30(0.67) | 0.63(1.36) | |
| 国DEN | -0.60(0.95) | 0.10(0.75) | -0.19(1.62) | |
| countryFIN | -0.55(0.89) | -0.04(0.67) | 2.40(1.32) | |
| countryFRA | -3.34(1.15) ** | -2.06(0.93) * | 1.39(2.07) | |
| countryGER | 0.48(0.85) | -1.40(0.72) | -0.65(1.33) | |
| countryHUN | -1.32(1.47) | -0.70(1.16) | 0.65(2.39) | |
| countryITA | -2.08(1.08) | -4.78(0.82) *** | -2.02(1.62) | |
| countryJPN | -4.13(1.26) ** | -6.52(0.94) *** | -2.27(1.98) | |
| 国KAZ | -1.23(0.95) | -1.82(0.79) * | 1.79(1.58) | |
| countryLAT | -0.73(0.95) | -1.39(0.75) | -3.42(1.49) * | |
| countryNOR | -3.25(1.07) ** | -1.06(0.85) | -0.10(1.66) | |
| countryPOL | 0.82(1.89) | -0.58(1.55) | 0.37(2.97) | |
| countrySLO | -1.57(0.99) | -1.54(0.79) | -2.25(1.66) | |
| countrySUI | -1.98(0.91) * | -2.36(0.71) *** | 1.12(1.47) | |
| countrySVK | 2.94(0.87) *** | 0.81(0.67) | -0.70(1.50) | |
| countrySWE | 0.75(0.81) | 1.24(0.65) | 1.37(1.33) | |
| countryUKR | -1.37(1.01) | -1.77(0.80) * | -3.71(1.66) * | |
| 国USA | 0.76(0.78) | -0.08(0.62) | 2.58(1.26) * | |
| R 2 | 0.09 | 0.10 | 0.24 | |
| 調整 R 2 | 0.07 | 0.09 | 0.20 | |
| 数 obs。 | 1094 | 1824 | 401 | |
| Rmse | 5.08 | 5.08 | 4.87 | |
| *** p <0.001、 ** p <0.01、 * p <0.05 | ||||
別のモデリングでは、1964年から1996年の出生時のコホートでは、2001年から2016年の世界選手権に参加するホッケー選手の平均成長率が、防御側では小数あたり0.4 cm、攻撃側では0.7 cm、(!)ゴールキーパー。 30年以上にわたり、ゴールキーパーの平均成長率は7 cm増加しました!
これらの変化を人口平均と比較する時が来ました。
人口との比較
回帰分析の結果は、重要なクロスカントリーの違いを記録しています。 したがって、特定の国のホッケー選手と同じ国の男性人口とを国ごとに比較するのは理にかなっています。
ホッケー選手の成長を平均的な男性人口と比較するために、 関連する科学記事 ( PDF )のデータを使用しました。 記事からデータをコピーし(素晴らしいタブラプログラムを使用) 、パブリックドメインに投稿しました 。
# download the data from Hatton, TJ, & Bray, BE (2010). # Long run trends in the heights of European men, 19th–20th centuries. # Economics & Human Biology, 8(3), 405–413. # http://doi.org/10.1016/j.ehb.2010.03.001 # stable URL, copied data (https://dx.doi.org/10.6084/m9.figshare.3394795.v1) df_hb <- read.csv('https://ndownloader.figshare.com/files/5303878') df_hb <- df_hb %>% gather('country','h_pop',2:16) %>% mutate(period=paste(period)) %>% separate(period,c('t1','t2'),sep = '/')%>% transmute(cohort=(as.numeric(t1)+as.numeric(t2))/2,country,h_pop) # calculate hockey players' cohort height averages for each country df_hoc <- dfu %>% group_by(country,cohort) %>% summarise(h_hp=mean(av.height)) %>% ungroup()
残念ながら、人口増加ダイナミクスに関するデータは、私のホッケーデータセットの8か国(オーストリア、デンマーク、フィンランド、フランス、ドイツ、イタリア、ノルウェー、スウェーデン)としか交差していません。
# countries in both data sets both_cnt <- levels(factor(df_hb$country))[which(levels(factor(df_hb$country)) %in% levels(df_hoc$country))] both_cnt
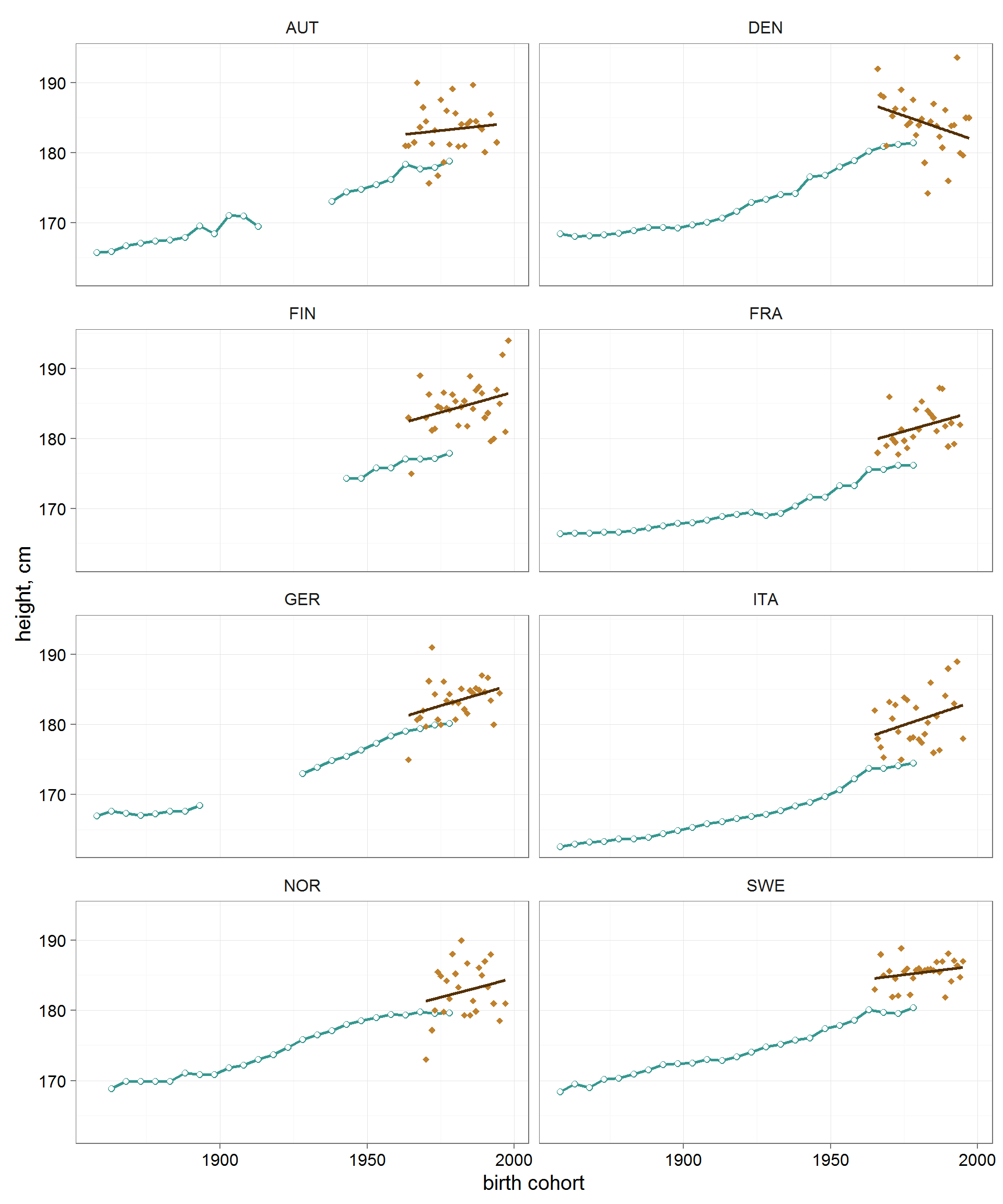
gg_hoc_vs_pop <- ggplot()+ geom_path(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop), color=brbg11[9],size=1)+ geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop), color=brbg11[9],size=2)+ geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop), color='white',size=1.5)+ geom_point(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp), color=brbg11[3],size=2,pch=18)+ stat_smooth(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp), method='lm',se=F,color=brbg11[1],size=1)+ facet_wrap(~country,ncol=2)+ ylab('height, cm')+ xlab('birth cohort')+ theme_few(base_size = 15)+ theme(panel.grid=element_line(colour = 'grey75',size=.25))
分析したすべての国で、ホッケー選手は標準的な統計の男性よりも2〜5 cm高いですが、これは驚くことではありません-スポーツにはかなりの選択があります。
別のことは注目に値します。 先進国では、20世紀初頭に男性の人口増加が特に急速に増加しました。 1960年代頃のコホートでは、男性の成長はプラトーに近づき、急速に増加しなくなりました。 (何らかの理由でデンマークを除く)すべての国のホッケー選手の平均的な成長傾向は、男性人口全体の長年の傾向を継続しているようです。
20世紀前半に生まれたヨーロッパ人のコホートでは、平均的な成長の成長率は、国に応じて10年あたり1.18〜1.74 cmの範囲でした(図7)。 1960年代以来、この指標は10年間で0.15〜0.80のレベルまで低下しています。

# growth in population df_hb_w <- df_hb %>% spread(cohort,h_pop) names(df_hb_w)[2:26] <- paste('y',names(df_hb_w)[2:26]) diffs <- df_hb_w[,3:26]-df_hb_w[,2:25] df_hb_gr<- df_hb_w %>% transmute(country, gr_1961_1980 = unname(apply(diffs[,22:24],1,mean,na.rm=T))*2, gr_1901_1960 = unname(apply(diffs[,9:21],1,mean,na.rm=T))*2, gr_1856_1900 = unname(apply(diffs[,1:8],1,mean,na.rm=T))*2) %>% gather('period','average_growth',2:4) %>% filter(country %in% both_cnt) %>% mutate(country=factor(country,levels = rev(levels(factor(country)))), period=factor(period,labels = c('1856-1900','1901-1960','1961-1980'))) gg_hb_growth <- ggplot(df_hb_gr, aes(x=average_growth,y=country))+ geom_point(aes(color=period),size=3)+ scale_color_manual(values = brbg11[c(8,3,10)])+ scale_x_continuous(limits=c(0,2))+ facet_wrap(~period)+ theme_few()+ xlab("average growth in men's height over 10 years, cm")+ ylab(NULL)+ theme_few(base_size = 20)+ theme(legend.position='none', panel.grid=element_line(colour = 'grey75',size=.25))
人口の停滞傾向を背景に、ホッケー選手の成長の増加は非常に印象的です。 そして、ゴールキーパー間の加速は一般に前例のないものです。
選択を忘れないでください。 人口とホッケー選手の傾向の違いは、選択の増加を示している可能性があります。ホッケーを成功させるには、さらに大きな成長が必要です。
スポーツ選択
このトピックに関する科学文献を見ると、 驚くべき結果に出会いました。 プロスポーツでは、年の前半に生まれた人が圧倒的に多いことがわかります。 これは、スポーツ部門が原則として出生コホートの子供のチームを形成するという事実によって説明されます。 したがって、年の初めに生まれた人は常に彼らの後ろにもう少し多くの時間を費やしています。 データセットでこの結果を確認するのは簡単です。

# check if there are more players born in earlier months df_month <- df %>% mutate(month=month(birth)) %>% mutate(month=factor(month,levels = rev(levels(factor(month))))) gg_month <- ggplot(df_month,aes(x=factor(month)))+ geom_bar(stat='count',fill=brbg11[8])+ scale_x_discrete(breaks=1:12,labels=month.name)+ xlab('month of birth')+ coord_flip()+ theme_few(base_size = 20)+ theme(legend.position='none', panel.grid=element_line(colour = 'grey75',size=.25))
確かに、分布はかなり早い時期に偏っています。 数十年ごとにデータを分解すると、肉眼で見ると、時間とともに効果が強まることがわかります(図9)。 間接的に、これはホッケーの選択が厳しくなっていることを示しています。

# facet by decades df_month_dec <- df_month %>% mutate(dec=factor(substr(paste(cohort),3,3),labels = paste('born in',c('1960s','1970s','1980s','1990s')))) gg_month_dec <- ggplot(df_month_dec,aes(x=factor(month)))+ geom_bar(stat='count',fill=brbg11[8])+ scale_x_discrete(breaks=1:12,labels=month.abb)+ xlab('month of birth')+ facet_wrap(~dec,ncol=2,scales = 'free')+ theme_few(base_size = 20)+ theme(legend.position='none', panel.grid=element_line(colour = 'grey75',size=.25))
未来のために
物理データがホッケー選手のゲーム統計に影響するかどうかを確認するのは興味深いでしょう。 非常にまともな科学雑誌に掲載された面白い記事に出くわしました。著者は、ホッケー選手の顔の割合とゲームあたりのペナルティ時間の平均数との相関関係を発見しました。
再現性
私の記事の結果を再現した完全なRスクリプトはこちらです。
使用済みバージョンR-3.2.4
2016-03-14現在のすべてのパッケージ。 パッケージの非互換性の場合、対応する日付でチェックポイントパッケージを使用すると、このコードが再現されることが保証されます。


