始める前に、問題をすぐに説明したいと思います。 問題自体は単純ですが、ポイントのセットとこれらのポイントが接続される順序があります。 そして、私たちがメンバーシップをテストしている点が与えられます。 多角形は閉じられており、一般的な場合、多角形のエッジは互いに交差していない、つまり、自己交差していることはありません。 頂点の数に制限はありません。つまり、100万の頂点を持つポリゴンを簡単に定義できます。 ユーザーが何を理解しているのかを私たちに尋ねないことを願っていますが、これも保証できません。 さらにもう1つ微妙な点があります。コンピューターグラフィックスを使用しているため、浮動小数点演算を使用しているため、数値を非常に正確に操作できますが、エラーは発生しません。
さて、問題をある程度決定しました。次に、どのような解決方法が存在するかを見てみましょう。
方法1.光線追跡
まず、グラフィックとゲームの世界で最も人気があると考えられているもの、つまりレイトレーシングから始めます。 つまり、アルゴリズムは次のように説明できます。
- テストされたポイントから、あらかじめ決められた方向または任意の方向にビームを発行します。
- ポリゴンとの交点の数をカウントします。
- 交差点の数が偶数であれば、私たちは外にいます。 交差点の数が奇数の場合、内側にいます。
簡単そうですね。 実際、これが最も簡単な方法です。 その結果、セグメント(ポリゴンフェース)とレイの特定の数の交点、つまり、実際には2本の線の交点になり、レイとセグメントに属する結果ポイントをテストします。 最も単純な場合、すべてのセグメントでビームを交差させる必要があります。ツリー(2次、バイナリ、またはBVH)を使用する場合、この数を減らすことができます。 一般に、彼らはこのアルゴリズムのアルゴリズムの複雑さはO(log n)であると言います。ここで、nはポリゴンのエッジの数です。
この方法は単純ですが、残念ながら、一般的な場合には使用しない方が良いです。 この理由は、ポリゴンの頂点またはレイと部分的に一致するエッジを交差させる場合です。 これを例で説明します。
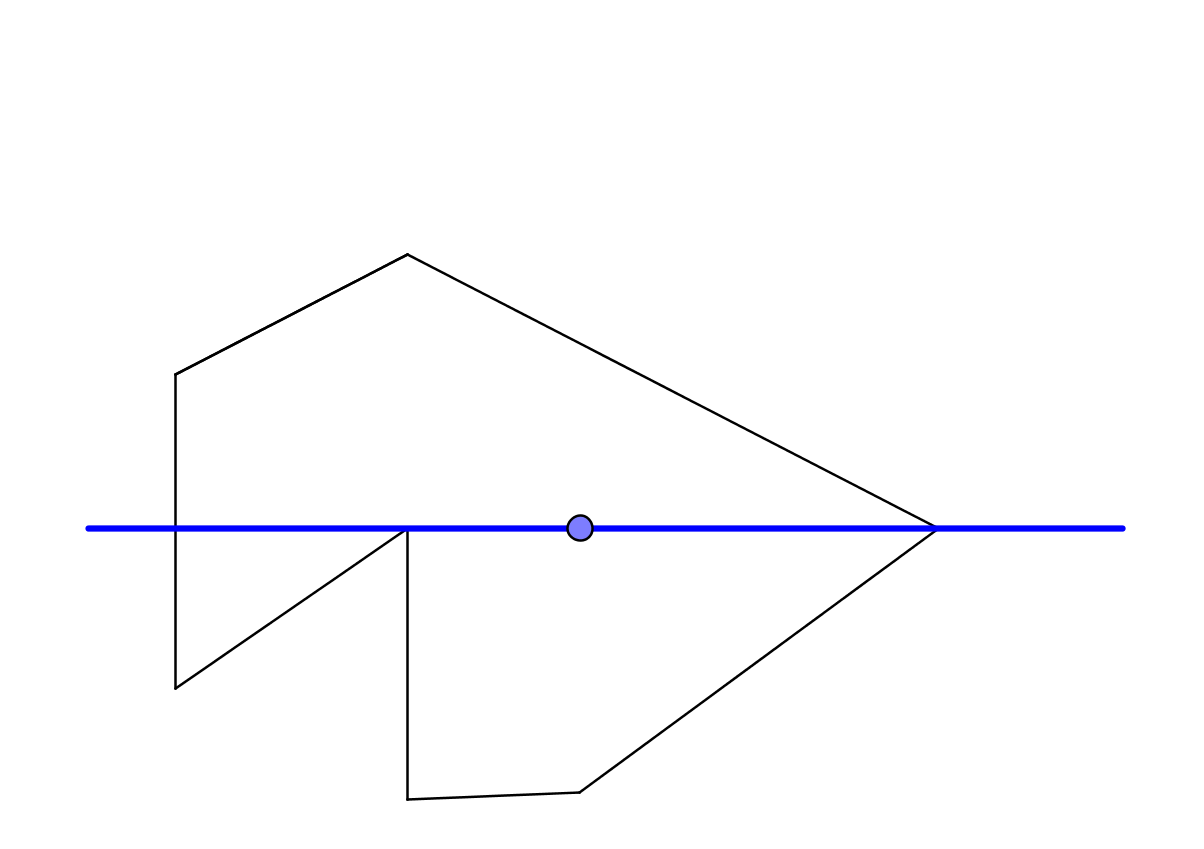
ポリゴンがあり、ポイントがあるとします。 最初に、方向がx軸に沿っていることに同意しました。 x軸の正の方向のポイントからレイを解放すると、レイは頂点でポリゴンと安全に交差します。 これは、この状況をどのように正確にチェックするのかという疑問を投げかけます。 浮動小数点数を使用していることを忘れないでください。小さなエラーが発生する可能性があります。 幾何学の概念だけでなく、数字でも操作できるように、分析幾何学の世界に移りましょう。
各セグメントの方程式(ポリゴンフェース): a + t( b - a )、ここでaはセグメントの一端の座標、 bはセグメントの他端の座標です。 明らかに、光線がセグメントと交差する場合、tは区間[0,1]になければなりません。 光線で頂点を横切る場合、t = 0またはt = 1です。これは数学の理想的な世界です。 コンピューター代数の現実の世界では、t = 1e-10のようなものになるかもしれません。 またはt = -1e-10。 または0.99999999999998。 または1.000000000000001。 2本の線の交点には分割手順が含まれているため、これは簡単に起こります。 そして、何をすべきか? コンピューターを信頼し、厳密にゼロ以上または厳密に単一以下である場合、これを交差と見なし、そうでない場合は考慮しないと仮定しますか? 一方のエッジがパラメーターt = -1e-20で、もう一方のエッジがt = 1.000000000000000001であるという状況を信頼しました。 その結果、これは交差点とは見なされず、この場合、ビームは正常にスリップし、結果は正しくありません。
別の方向を見てみましょう。 マイナス方向にビームを送信しました。 そこもあまり良くありません-光線はポリゴン内部の頂点を横切ります。 また、何でもかまいません。 水平方向の代わりに、垂直方向を取りますか? ピークを二度と越えないという保証はありません。 上で具体的に選択した例では、y軸に平行で上から下へ向かう光線との交点も頂点でポリゴンと交差するように、点が選択されています。
そして、トップと交差することが悪いと思うなら、他に何が起こるか見てください:
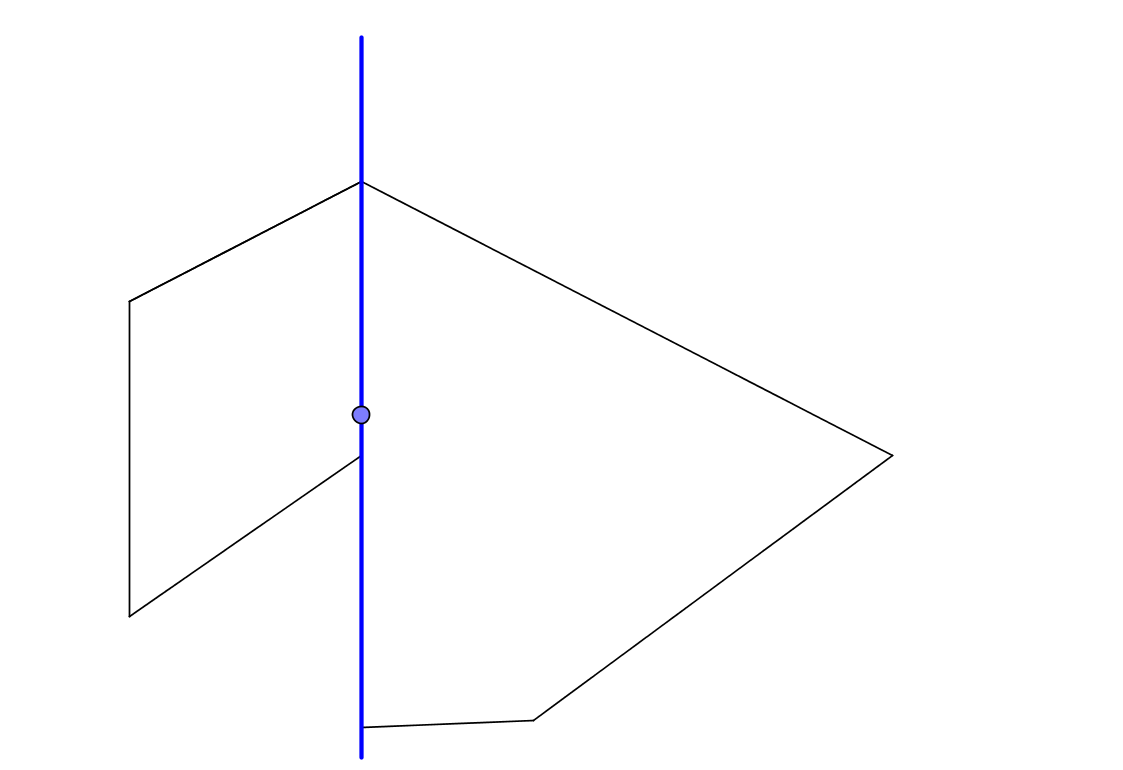
ここでは、この光線と一致する線分で光線を交差させます。 この場合の対処方法 そして、それが一致しないが、ほぼ一致する場合は? そして、ポリゴンには多くのほとんど縮退したエッジがあると想像してください。
この状況全体で最も悲しいことは、「単純な目標のために非常に単純なものが必要です。この状況は私には影響しません」ということです。 マーフィーの法則によれば、残念ながら、そのような状況はあなたがそれをまったく期待しないときはいつでも起こります。 そのため、2番目の方法にスムーズに移行します。
方法2.ニアポイントとその法線
一般に、このメソッドにはひどい名前の角度加重擬似法線があり、いわゆる符号付き距離フィールドの概念で接続されています。 しかし、もう一度私は誰も怖がらせたくないので、それをちょうど近点とその法線(つまり、垂直ベクトル)にします。
この場合のアルゴリズムは次のとおりです。
- テストしたポイントについては、ポリゴン上の最も近いポイントを探します。 同時に、最も近いポイントはセグメント上だけでなく頂点上にもあることを覚えています。
- 最も近い点の法線を探しています。 近点がエッジにある場合、法線はエッジに垂直で、ポリゴンの外側を向くベクトルです。 近点が頂点の1つである場合、法線は頂点に隣接するエッジの平均ベクトルです。
- 最も近い点の法線とテストされた点から最も近い点までのベクトルとの間の角度を計算します。 角度が90度未満の場合は内側になり、そうでない場合は外側になります。
さらに、角度自体は必要ありません。この角度の余弦を確認するだけで十分です。 正の場合-内側、負の場合-外側。 そして、コサインにのみ関心があるため、2つのベクトル間のスカラー積の符号を本質的に計算します。
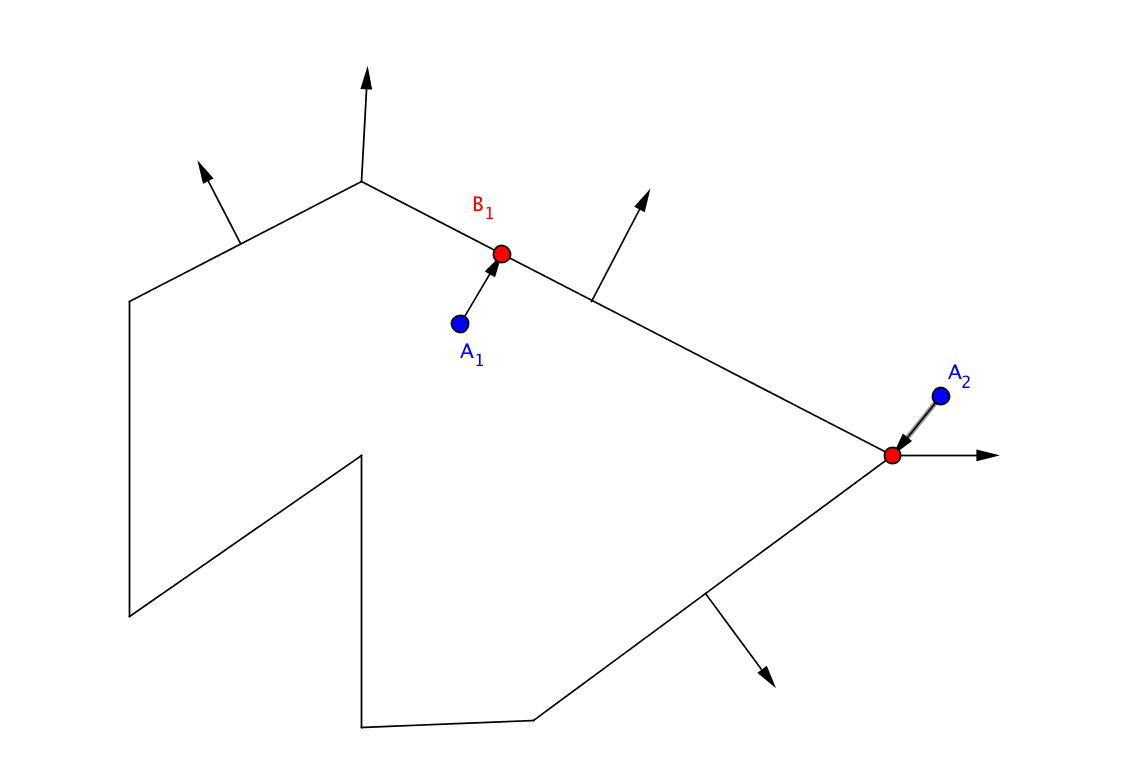
例を考えてみましょう。 ポイントA1、それに最も近いポイントはエッジ上にあります。 すべてを正しく行うと、エッジの法線は、テストされたポイントから最も近いベクトルに平行になります。 ポイントA1の場合、ベクトル間の角度=0。または、ほとんどゼロです。これは、浮動小数点演算によりすべてが可能なためです。 90度未満、テストポイントA1は内側です。 テストポイントA2。 その最も近い点は頂点であり、法線はこの頂点に隣接するエッジの平均法線です。 2つのベクトルのスカラー積は負でなければなりません。 外にいる。
したがって、メソッドの本質を整理したようです。 パフォーマンスと浮動小数点の問題はどうですか?
ツリーを使用してエッジ情報を保存する場合、ポイントトレースと同様に、パフォーマンスはO(log n)です。 計算の観点からは、同様の複雑さを持ちますが、トレースよりも多少遅くなります。 まず、ポイントとエッジの間の距離は、2本の線を交差させるよりも少し高価な操作であるためです。 この方法では、通常、ポリゴンのエッジ付近で浮動小数点の問題が発生します。 さらに、エッジに近いほど、符号が誤って決定される可能性が高くなります。 幸いなことに、エッジに近いほど、距離は短くなります。 つまり、たとえば、取得した距離が所定の最小値(DBL_EPSILONやFLT_EPSILONなどの定数)より小さい場合、ポイントはエッジに属します。 そして、エッジに属している場合は、ポリゴンの一部にエッジがあるかどうか(原則として一部)を判断します。
前の方法を説明すると、欠点についてかなり多くのことが言われています。 この方法のいくつかの欠点を挙げる時が来ました。 まず、この方法では、エッジのすべての法線を正しい方向に向ける必要があります。 つまり、私たちが外にいるか内にいるかを判断する前に、これらの法線とその正しい方向の計算に関するいくつかの作業を実行する必要があります。 非常に頻繁に、特に入り口に大きな山と縁のダンプがある場合、このプロセスは必ずしも簡単ではありません。 1つのポイントのみを決定する必要がある場合、通常のオリエンテーションプロセスでは、他の何かに費やすことができるほとんどの時間がかかる可能性があります。 また、この方法は、自己交差のあるポリゴンが入力に与えられるときは本当に好きではありません。 初めに、私たちの問題ではそのようなケースは考慮されていないと述べましたが、考慮された場合、この方法は完全に明白でない結果を生み出す可能性があります。
しかし、一般に、この方法は悪くありません。特に、入力に多数の頂点とエッジを持つポリゴンがあり、多くのポイントが属する場合はそうです。 ポイントが少ない場合、レイトレーシングは不安定ですが、多かれ少なかれ信頼できるもの、つまり3番目の方法が必要です。
方法3.ポリゴンに相対的なポイントのインデックス
この方法は古くから知られていますが、基本的には前の2つほど効果的ではないため、ほとんどの部分で理論的にはそのままです。 その本質は「指の上」です。 テスト対象のポイントを中心とした単位円を取ります。 次に、頂点とテストポイントを通過する光線を使用して、ポリゴンの各頂点をこの円に投影します。 このようなもの:

図では、ポイントP1、P2などはポリゴンの頂点であり、ポイントP1 '、P2'などは円への投影です。 ポリゴンのエッジを考慮すると、ある頂点から別の頂点に移動するときに、回転が反時計回りまたは時計回りのどちらで発生するかを投影から判断できます。 反時計回りの回転は正の回転と見なされ、時計回りの回転-負の回転と見なされます。 各エッジに対応する角度は、このエッジの頂点の投影を通る円のセグメント間の角度です。 ターンは正または負になる可能性があるため、角度は正または負になる可能性があります。
その後、これらすべての角度が追加される場合、合計は、内側のポイントでは+360または-360度、外側のポイントでは0になります。 ここにはプラスまたはマイナスの理由があります。 走査順序を指定するときに、ポリゴンが反時計回りにバイパスされる場合、+ 360になります。 ポリゴン内のエッジをトラバースする順序が反時計回りの場合、-360が取得されます。 数値エラーを避けるために、彼らは通常これを行います:結果の量を360で割り、最も近い整数に導きます。 ちなみに結果の数値は、まさにポイントのインデックスです。 結果は次の3つのうちのいずれかです。-1は内側にあり、ポリゴンを時計回りに移動することを意味し、0は外側にあることを、+ 1は外側にあることを意味します。 それ以外は、どこかで間違っていたか、入力データが間違っていることを意味します。
この場合のアルゴリズムは次のとおりです。
- 角度の合計を0に設定します。
- ポリゴンのすべてのエッジに対して:
- スカラー積を使用して、テストポイントから始まり、エッジの端で終わるベクトルが形成する角度を計算します。
- これらの同じベクトルのベクトル積を計算します。 そのz成分が正の場合、角度の合計に角度を追加し、そうでない場合は同じ合計から減算します。
ラジアンで数える場合は合計を2で除算し、度で数える場合は360で除算します。 後者はほとんどありませんが、突然です。
結果を最も近い整数に丸めます。 +1または-1は、内部にいることを意味します。 0は外にいることを意味します。
例を考えてみましょう。 順序が反時計回りに設定されているポリゴンがあります。 テストしているポイントAがあります。 テストのために、まずベクトルAP1とAP2の間の角度を計算します。 これらの同じベクトルのベクトル積は私たちを見るので、合計に加算します。 さらに進んで、AP2とAP3の間の角度を検討します。 ベクトル積が私たちを見ているので、結果の角度を引きます。 などなど。
この特定の図について、すべてを計算しましたが、これが何が起こったのかです:
ポイントA
(AP1、AP2)= 74.13、(AP2、AP3)= 51.58、(AP3、AP4)= 89.99、(AP4、AP5)= 126.47、(AP5、AP1)= 120.99。
合計= 74.13-51.58 + 89.99 + 126.47 + 120.99 = 360 360/360 = 1ポイント-内部。
ポイントB
(BP1、BP2)= 44.78、(BP2、BP3)= 89.11、(BP3、BP4)= 130.93、(BP4、BP5)= 52.97、(BP5、BP1)= 33.63。
sum = -44.78 + 89.11-130.93 + 52.97 + 33.63 = 0 ポイントは外側です。
そして伝統的に、我々はこのアプローチの長所と短所を説明しています。 短所から始めましょう。 この方法は数学的には単純ですが、パフォーマンスの点ではそれほど効果的ではありません。 まず、アルゴリズムの複雑さはO(n)であり、何と言っても、ポリゴンのすべてのエッジを整理する必要があります。 第二に、角度を計算するには、逆余弦演算とルートを取る2つの演算を使用する必要があります(スカラー積の公式と、理由が分からない人との角度との関係)。 これらの操作は速度の点で非常に高価であり、さらに、それらに関連するエラーが重大になる可能性があります。 そして第三に、アルゴリズムはエッジにあるポイントを直接決定しません。 外部または内部のいずれか。 3番目はありません。 ただし、最後の欠点は簡単に判断できます。少なくとも1つの角度が180度に等しい(またはほぼ等しい)場合、これは自動的にエッジを意味します。
この方法の欠点は、その利点によっていくらか相殺されます。 まず、これは最も安定した方法です。 入力ポリゴンが正しい場合、エッジ上のポイントを除き、結果はすべてのポイントに対して正しいですが、上記を参照してください。 さらに、このメソッドを使用すると、誤った入力データを部分的に処理できます。 ポリゴンは自己交差していますか? 問題ではありませんが、ほとんどのポイントを正しく決定する可能性が高い方法です。 多角形が閉じていない、またはまったく多角形ではなく、意味のないセグメントのセットですか? この方法は、多くの場合にポイントを正しく決定します。 一般に、この方法はすべての人に適していますが、時間がかかり、逆余弦の計算が必要です。
このレビューをどのように終了しますか? また、ポイントがポリゴンに属しているかどうかを判断する問題を解決する方法が1つも2つも存在しないという事実。 それらは異なる目的に役立ち、速度が重要な場合により適しているものもあれば、品質が重要な場合に適しているものもあります。 予測できない入力データがあり、浮動小数点演算にエラーが発生するコンピューターで作業することを忘れないでください。 速度と品質が必要な場合は、まったく問題ではありません。レイトレーシングが役立ちます。 ほとんどの実際のアプリケーションでは、近点で通常の方法が最も役立つでしょう。 そもそも入力データが不明瞭な場合の判定の精度である場合、ポイントインデックスメソッドが役立ちます。
ご質問がある場合は、お問い合わせください。 ジオメトリやグラフィックスに関連する同様の問題を扱う人として、できる限りお手伝いさせていただきます。