理論のビット
2値化プロセスは、カラー(またはグレースケール)画像を2色の白黒に変換することです。 このような変換の主なパラメータは、各ピクセルの輝度を比較する値であるしきい値tです。 比較によると、ピクセルには0または1の値が割り当てられます。グローバルとローカルの2つのグループに分けることができるさまざまな2値化方法があります。 最初のケースでは、2値化のプロセス全体でしきい値は変更されません。 2番目の方法では、画像が領域に分割され、それぞれの領域でローカルしきい値が計算されます。
二値化の主な目標は、作業する必要がある情報の量を根本的に減らすことです。 簡単に言えば、2値化が成功すると、その後の画像の処理が大幅に簡素化されます。 一方、2値化プロセスの失敗は、改行、意味のある詳細の喪失、オブジェクトの完全性の違反、ノイズ、背景の不均一性による予測できない文字の歪みなどの歪みを引き起こす可能性があります。 さまざまな二値化方法には弱点があります。たとえば、大津法は、細部の損失と近くのシンボルの「くっつき」につながる可能性があり、Niblack法は、コントラストの低い背景の不均一性の場合に偽オブジェクトの出現を伴います。 したがって、各メソッドはそのフィールドに適用する必要があります。
テスト対象
現在、私は「スマートホーム」の一般的なアイデアの一部として、家電製品の測定値の認識に取り組んでいます。 グループが使用する画像の例を次に示します。

写真は、暗闇の部屋で暗闇の夜に撮影されました。 側面のLED照明は非常に不均一な背景を作成し、カメラとインストルメントパネルの間にケイ酸塩ガラスがあります。これにより、背景領域に追加のノイズと偽の形成が発生します。 私たちのタスクは、テキスト認識のために画像を準備することです。
ここでローカルメソッドを使用することは論理的であり、それらは適応的でもあります。 Niblackメソッドは、従来のローカルアルゴリズムの中で最速と見なされますが、低コントラストの背景不規則性ではうまく機能しません。 この欠点を修正するために、賢明な人々はニブル法と呼ばれるニブル法のいくつかの修正を開発しました。 私の場合、そのうちの1つであるクリスチャン法は、ほとんどのサンプルで良好な結果を示し、作業オプションとしてほぼ受け入れられました。 ただし、他のサンプルでは、このアルゴリズムを適用した後、歪みが現れました。

a)ニブラック法b)クリスチャン法
ブラッドリー法の本質
しきい値とピクセルの明るさという2つの値を比較すること自体が基本的なタスクです。 これはポイントではありません。 困難なのは、文字を背景だけでなく、ノイズ、影、まぶしさ、その他の情報のゴミからも確実に分離するしきい値を見つけることにあります。 多くの場合、彼らは数学的統計の方法に頼っています。 ブラッドリー法では、反対側から-積分画像の側から行きます。
インテグラルイメージ
統合された画像は、ピクセル値の合計を見つけるための効果的で高速な(画像を1回パスするだけでなく)方法であるだけでなく、特定の画像領域内の平均輝度値を見つける簡単な方法でもあります。
どのように機能しますか? はい、小学校。 8ビットのグレースケールイメージがあるとします(式I = 0.2125R + 0.7154G + 0.0721Bを使用して、カラーイメージをグレースケールに変換できます)。 この場合、積分画像要素の値は次の式で計算されます。
S(x、y)= I(x、y)+ S(x-1、y)+ S(x、y-1)-S(x-1、y-1);
ここで、Sは指定されたピクセル位置の前の反復の結果、Iは元の画像のピクセルの明るさです。 座標が画像を超える場合、それらはゼロと見なされます。 「指で」この方法の本質を下の図に示します。
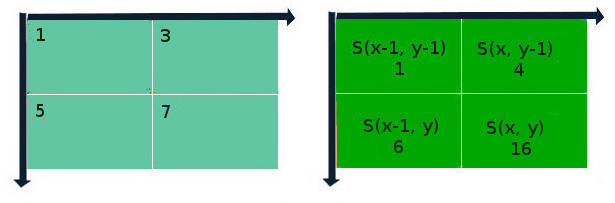
ライフハックは、画像の積分マトリックスをコンパイルすると、この画像内の任意の長方形領域のピクセル値の合計をすばやく計算できるという事実にあります。 ABCDを関心のある長方形の領域にします。
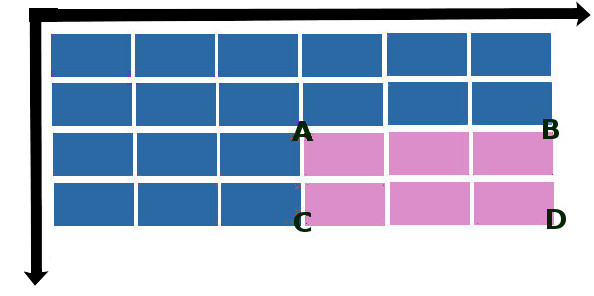
次に、この領域の合計輝度Sは次の式で計算されます。
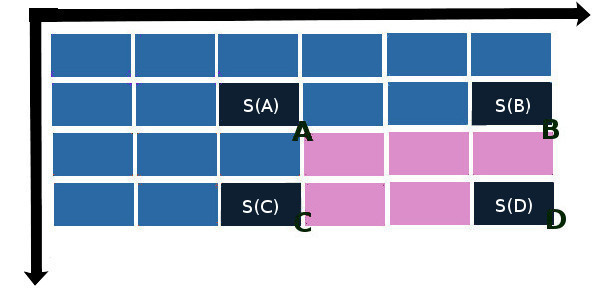
S(x、y)= S(A)+ S(D)-S(B)-S©
ここで、S(A)、S(B)、S©およびS(D)は、長方形の辺の交点から「北西」方向の積分行列の要素の値です。
実装
ここまで読んだら、ほとんどBradleyアルゴリズムを理解していました。 その後、すべてが簡単です。 画像を側面dのいくつかの領域に分割し、この領域のピクセルImの値の合計の平均を取り、特定の値tを追加し、各ピクセルの値と結果の結果を比較します。 Im + t-必要なしきい値です。 BradleyとRothは、それぞれdとtの値を取ります。それぞれ、画像の幅の1/8と、領域内のピクセルの平均輝度の15%です。 しかし、一般的に言えば、これらのパラメーターは両方とも、特定の状況に応じて変化する可能性があります。 したがって、オブジェクトのサイズが辺がdに等しい正方形よりも大きい場合、このオブジェクトの中心はアルゴリズムによって背景として受け入れられ、dの値を減らすことで問題は解決されますが、画像の細部が失われる可能性があります。
そして、これは私たちの例でどのように見えるかです:

中央値フィルタリング後:

C ++でのBradley-Rothアルゴリズムの実装を以下に示します。
void Bradley_threshold(unsigned char* src, unsigned char* res, int width, int height) { const int S = width/8; int s2 = S/2; const float t = 0.15; unsigned long* integral_image = 0; long sum=0; int count=0; int index; int x1, y1, x2, y2; // integral_image = new unsigned long [width*height*sizeof(unsigned long*)]; for (int i = 0; i < width; i++) { sum = 0; for (int j = 0; j < height; j++) { index = j * width + i; sum += src[index]; if (i==0) integral_image[index] = sum; else integral_image[index] = integral_image[index-1] + sum; } } // for (int i = 0; i < width; i++) { for (int j = 0; j < height; j++) { index = j * width + i; x1=i-s2; x2=i+s2; y1=j-s2; y2=j+s2; if (x1 < 0) x1 = 0; if (x2 >= width) x2 = width-1; if (y1 < 0) y1 = 0; if (y2 >= height) y2 = height-1; count = (x2-x1)*(y2-y1); sum = integral_image[y2*width+x2] - integral_image[y1*width+x2] - integral_image[y2*width+x1] + integral_image[y1*width+x1]; if ((long)(src[index]*count) < (long)(sum*(1.0-t))) res[index] = 0; else res[index] = 255; } } delete[] integral_image; }
長所と短所
Bradley-Rothメソッドの利点は、実装の容易さと実行の高速性です。 ほとんどの場合、パラメーターを選択する必要はありません。 この方法は、異種のバックグラウンドでうまく機能します。
最後の利点は論理的にブラッドリー法の欠点、つまり低コントラストの画像の詳細に対する感度が低いことを意味します。
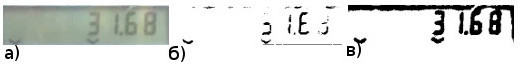
a)元の画像b)ブラッドリー法c)クリスチャン法
参照:
http://citeseerx.ist.psu.edu-Bradley and Rothによるオリジナル記事(英語)
https://computersciencesource.wordpress.com-著者は統合画像の本質を非常に明確に説明しています(英語)
http://web.mit.edu/mfeng/www/papers/mengling_ieice.pdf-Nibbleメソッドの概要(およびそれらも)数式と著者の記事へのリンク(英語)
http://liris.cnrs.fr/christian.wolf/software/binarize/-Christian Wulfは、Christian Wolfe、Niblek、Savolaのアルゴリズムを実装しています(C ++)