はじめに

私は数学者プログラマーです。 「何も分からない！」と言うことを学んだとき、私は自分のキャリアで最大の飛躍を遂げました。今、科学者に自分が講義をしていること、それが何であるかわからないことを伝えることを恥ずかしく思いません。 そして、それは非常に難しいです。 はい、無知を認めることは難しく、恥ずかしいです。 誰が彼がそこで何かの基本を知らないことを認めたいです。 私の職業のおかげで、私は多くのプレゼンテーションと講義に出席しなければなりません。 科学の現在の状況の大きな問題は数学にあるので、私は理解していません。 彼女は、すべての学生が数学のすべての分野に絶対に精通していると仮定しています（これはばかげています）。 デリバティブが何であるかわからない（少し後である）ことを認めることは残念です。



しかし、私は乗算とは何なのかわからないと言うことを学びました。 はい、リー代数上の部分代数が何であるかはわかりません。 はい、なぜ二次方程式が人生で必要なのかわかりません。 ところで、あなたがあなたが知っていると確信しているなら、それから私たちは話すべきことがあります！ 数学は一連のトリックです。 数学者は大衆を混乱させ、脅迫しようとします。 混乱も評判も権威もありません。 はい、可能な限り最も抽象的な言語で話すことは名誉です。それはそれ自体完全なナンセンスです。



デリバティブとは何ですか？ ほとんどの場合、差分関係の限界について教えてくれます。 サンクトペテルブルク州立大学での最初の年に、 ヴィクトル・カヴィンはある点で関数のテイラー級数の最初のメンバーの係数として微分を定義しました（微分なしでテイラー級数を決定するのは別の体操でした）。 私はそのような定義を長い間笑いましたが、最終的にはそれが何であるか理解できませんでした。 導関数は、微分する関数がどれだけ関数y = x、y = x ^ 2、y = x ^ 3に似ているかの尺度にすぎません。



私は今、数学を恐れている学生に講義する名誉を持っています。 あなたが数学を恐れているなら、私たちはあなたの道にいます。 あなたがテキストを読み込もうとするとすぐに、それは過度に複雑であるように思われ、それからそれがひどく書かれていることを知っている。 私は、正確さを失わずに「指で」話すことのできない数学の単一の領域がないことを確認します。



近い将来の課題： 線形2次レギュレータとは何かを理解するよう生徒に指示しました。 恥ずかしがらずに、人生の3分間を過ごし、リンクをたどってください。 あなたが何も理解していない場合、あなたと私は途中です。 私（数学のプロ兼プログラマー）も何も理解していませんでした。 そして、あなたはそれをあなたの指で理解できることを保証します。 現時点ではそれが何であるかわかりませんが、私たちはそれを理解できると確信しています。



ですから、線形二次レギュレータは人生で決して習得できない恐ろしい白濁であるという言葉で恐怖に駆られて学生に読んでもらう最初の講義は最小二乗法です。 線形方程式を解く方法を知っていますか？ このテキストを読んでいる場合、ほとんどの場合そうではありません。



したがって、2つのポイント（x0、y0）、（x1、y1）、たとえば（1,1）と（3,2）が与えられますが、問題はこれらの2つのポイントを通る直線の方程式を見つけることです：







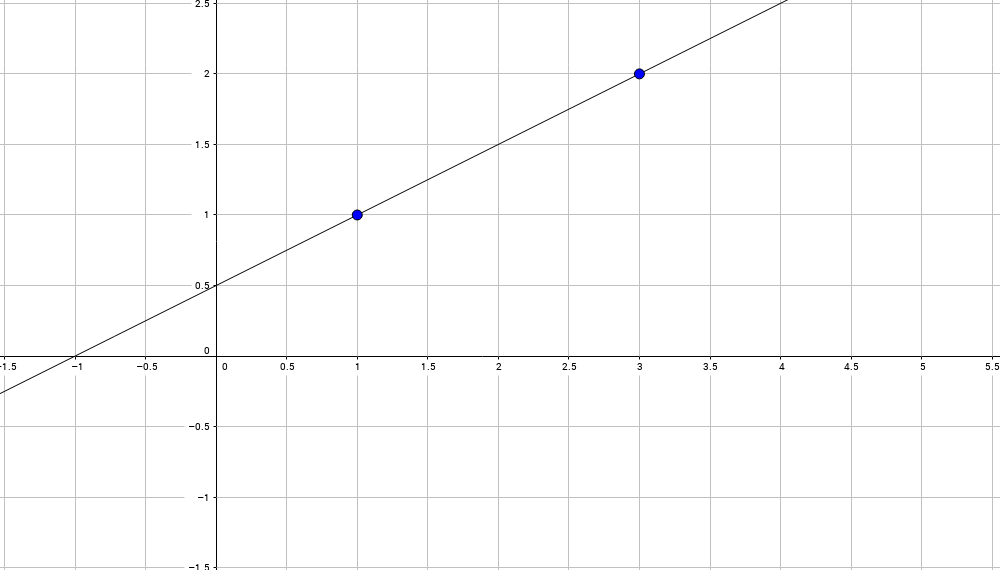
この行には、次のような式が必要です。







ここでは、アルファとベータは不明ですが、この行の2つのポイントがわかっています。







この方程式は、行列形式で記述できます。







ここで叙情的な余談を行う必要があります：マトリックスとは何ですか？ マトリックスは、2次元配列にすぎません。 これはデータを保存する方法です。これ以上値を添付しないでください。 特定のマトリックスをどのように正確に解釈するかは私たち次第です。 定期的に、線形マッピングとして、定期的に二次形式として、時にはベクトルのセットとして解釈します。 これはすべてコンテキストで明確になります。



特定の行列をシンボリック表現で置き換えましょう：







次に、（アルファ、ベータ）を簡単に見つけることができます。







以前のデータをより具体的に：











これは、ポイント（1,1）および（3,2）を通過する次の方程式を導きます。







さて、ここではすべてが明確です。 そして、 3つの点を通る直線の方程式を見つけましょう：（x0、y0）、（x1、y1）and（x2、y2）：







ああ、ああ、2つの未知数について3つの方程式があります！ 標準的な数学者は、解決策はないと言います。 プログラマーは何と言いますか？ そしてまず、彼は以前の方程式系を次の形式に書き直しました。







そして、彼は与えられた平等から最も逸脱しない解決策を見つけようとします。 ベクトル（x0、x1、x2）をベクトルi、（1,1,1）ベクトルj、（y0、y1、y2）ベクトルbと呼びましょう：







この場合、ベクトルi、j、bは3次元であるため、（一般的な場合）このシステムの解決策は存在しません。 任意のベクトル（アルファ\ * i +ベータ\ * j）は、ベクトル（i、j）に引き伸ばされた平面にあります。 bがこの平面に属さない場合、解はありません（方程式の等式に到達できません）。 どうする 妥協点を見つけましょう。 e（アルファ、ベータ）で、どの程度正確に等値に達しなかったかを示しましょう。







そして、このエラーを最小化しようとします：











明らかに、ベクトルeがベクトルiとjがまたがる平面に直交する場合、誤差は最小になります。







つまり、すべてのポイントからこのラインまでの距離の長さの平方和が最小になるようなラインを探しています。



更新：ここに私はわき柱があります、ラインへの距離は垂直投影ではなく、垂直に測定されるべきです。 このコメンテーターは正しいです。





言い換えれば（慎重に、形式化は不十分ですが、指では明確にする必要があります）：すべてのポイントペア間で考えられるすべての線を取り、すべての間の中間線を探します。







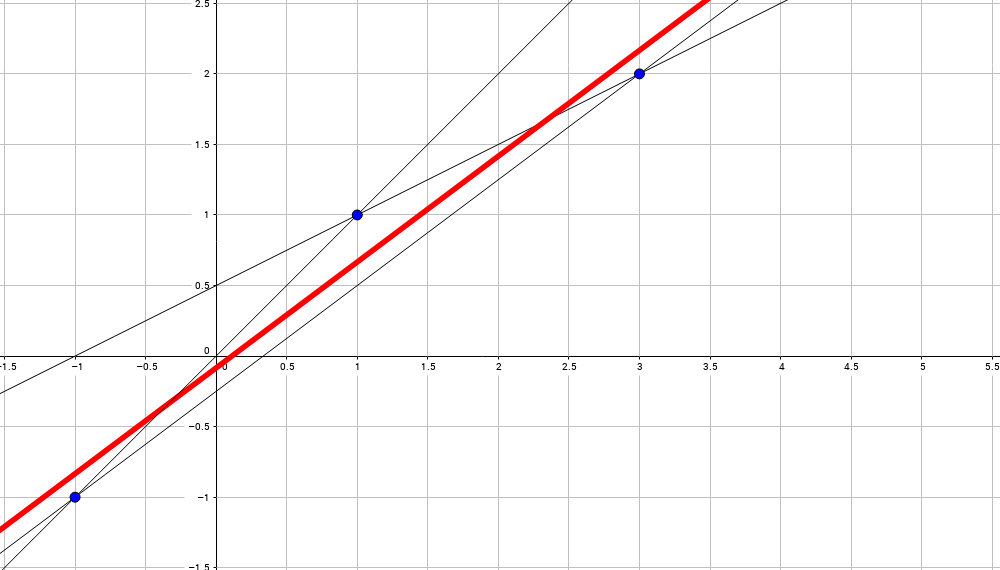
指に関する別の説明：すべてのデータポイント（ここでは3つあります）と探している直線の間にバネを付けます。平衡状態の直線はまさに探しているものです。

二次最小

そのため、与えられたベクトルbと、行列Aの列ベクトル（この場合（x0、x1、x2）および（1,1,1））に引き伸ばされた平面を持ち、最小の2乗長のベクトルeを探しています。 明らかに、最小値は、行列Aの列ベクトル上に引き伸ばされた平面に直交するベクトルeに対してのみ達成可能です。







つまり、次のようなベクトルx =（alpha、beta）を探しています。







このベクトルx =（alpha、beta）は二次関数の最小値であることを思い出す|| e（alpha、beta）|| ^ 2：





行列は2次形式を含めて解釈できることを思い出してください。たとえば、単位行列（（1,0）、（0,1））は関数x ^ 2 + y ^ 2として解釈できます。











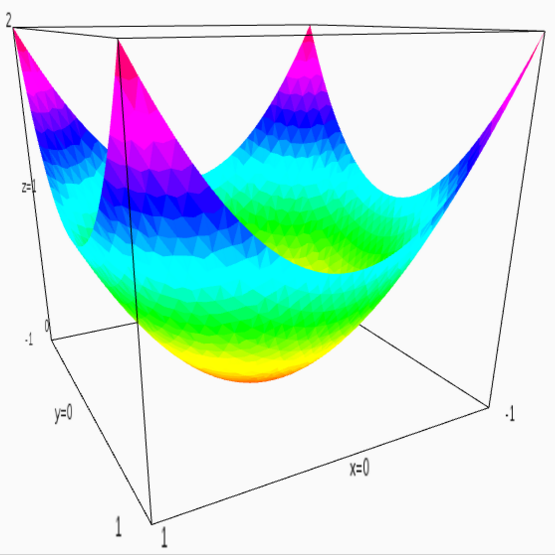
このすべての体操は、 線形回帰として知られています。

ディリクレ境界条件付きのラプラス方程式

今、最も単純な実際のタスク：特定の三角形の表面があり、それを滑らかにする必要があります。 たとえば、顔モデルをアップロードしましょう：







最初のコミットはこちらから入手できます 。 外部依存関係を最小限に抑えるために、ソフトウェアレンダラーのコードを使用しました。これについては、既にHabrで詳細に説明されています。 線形システムを解決するには、 OpenNLを使用しますが 、これは優れたソルバーですが、インストールが非常に困難です。2つのファイル（.h + .c）をプロジェクトのフォルダーにコピーする必要があります。 すべてのアンチエイリアスは、次のコードで実行されます。

    for (int d=0; d<3; d++) {
        nlNewContext();
        nlSolverParameteri(NL_NB_VARIABLES, verts.size());
        nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
        nlBegin(NL_SYSTEM);
        nlBegin(NL_MATRIX);

        for (int i=0; i<(int)verts.size(); i++) {
            nlBegin(NL_ROW);
            nlCoefficient(i, 1);
            nlRightHandSide(verts[i][d]);
            nlEnd(NL_ROW);
        }

        for (unsigned int i=0; i<faces.size(); i++) {
            std::vector<int> &face = faces[i];
            for (int j=0; j<3; j++) {
                nlBegin(NL_ROW);
                nlCoefficient(face[ j     ],  1);
                nlCoefficient(face[(j+1)%3], -1);
                nlEnd(NL_ROW);
            }
        }

        nlEnd(NL_MATRIX);
        nlEnd(NL_SYSTEM);
        nlSolve();

        for (int i=0; i<(int)verts.size(); i++) {
            verts[i][d] = nlGetVariable(i);
        }
    }

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

X, Y Z , . , , . n A , n b . , — .



A (faces.size()*3 = ) 1 -1, b . , : .



: , , .



:







, , . - :

        for (int i=0; i<(int)verts.size(); i++) {
            float scale = border[i] ? 1000 : 1;
            nlBegin(NL_ROW);
            nlCoefficient(i, scale);
            nlRightHandSide(scale*verts[i][d]);
            nlEnd(NL_ROW);
        }

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

A , , v_i = verts[i][d], 1000*v_i = 1000*verts[i][d]. ? . , , 1000*1000 . , , . :







:

                nlCoefficient(face[ j     ],  2);
                nlCoefficient(face[(j+1)%3], -2);

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, :







:







? , . , , - — . , . , . ? - .

.



, :







, .



:







:





, , , , :

    for (int i=0; i<w*h; i++) {
        if (m.get(i%w, i/w)[0]<128) continue;
        nlBegin(NL_ROW);
        nlCoefficient(i, 1);
        nlRightHandSide(a.get(i%w, i/w)[0]);
        nlScaleRow(100);
        nlEnd(NL_ROW);
    }

    for (int i=0; i<w-1; i++) {
        for (int j=0; j<h-1; j++) {
            for (int d=0; d<2; d++) {
                nlBegin(NL_ROW);
                int v1 = b.get(i,   j    )[0];
                int v2 = b.get(i+d, j+1-d)[0];
                nlCoefficient( i   + j     *w,  1);
                nlCoefficient((i+d)+(j+1-d)*w, -1);
                nlRightHandSide(v1-v2);
                nlScaleRow(10);
                nlEnd(NL_ROW);
            }
        }
    }

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:







.

, .. - , , . :



:







. () :







, - , :







, :







, :







:







, :







, , , - . - . :







, . , , .