はじめに
並べ替えネットワークは、比較操作が実行される順序とその数が、並べ替えられた配列の要素の値に依存しない並べ替えアルゴリズムの一種です。 大量のデータをソートするためのスケーラブルな並列アルゴリズムを作成できます。
ネットワークのソートでは、配列の各要素がコンパレーターによって順次処理されます。 コンパレーターは2つの要素を比較し、必要に応じてそれらを交換します。
通常、ソートネットワークは次のように表されます。 ソート可能な配列要素は水平データ線で示され、コンパレータは2行のみを接続する垂直セグメントで示されます。 次の図1は、3つの要素の並べ替えネットワークと配列順序の例を示しています。
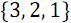 。 各データ行の値は、対応するコンパレーターがトリガーされると変化します。
。 各データ行の値は、対応するコンパレーターがトリガーされると変化します。
図1. 3つの要素の配列をソートするためのネットワーク。
現時点では、任意の数の入力に対して最小限の時間でネットワークを構築する方法は不明であるため、最速のスケーラブルなソートネットワークの1つと考えています。
Batcher Merger Exchange Sorting Network
ブッチャーネットワークは、最速のスケーラブルネットワークです。 ネットワークを構築するには、次の再帰アルゴリズムを使用します。
配列を並べ替えるとき
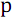 数字を持つ要素
数字を持つ要素 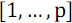 それは2つの部分に分けられるべきです:最初の休暇で
それは2つの部分に分けられるべきです:最初の休暇で 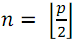 数字を持つ要素
数字を持つ要素  、そして2番目に
、そして2番目に 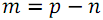 数字を持つ要素
数字を持つ要素 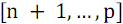 。 次に、各部分をソートし(関数B )、ソート結果を結合します(関数S )。
。 次に、各部分をソートし(関数B )、ソート結果を結合します(関数S )。
これらの関数をさらに詳しく考えてみましょう。
B ( 配列 )-行のグループをソートするためのネットワークの再帰的構築の機能。 配列を2つのサブ配列に再帰的に分割します。
 そして
そして 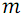 それぞれの要素の後に、これらのサブ配列に対してマージ関数Sを呼び出します。
それぞれの要素の後に、これらのサブ配列に対してマージ関数Sを呼び出します。
S ( up 、 down )-2つのグループの行の再帰的マージの機能。 奇数-偶数マージネットワークは、奇数の配列の要素を個別に結合し、偶数の配列を個別に結合します。その後、コンパレータの最終グループを使用して、隣接する要素と番号のペアが処理されます
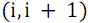 どこで
どこで 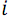 -からの自然数
-からの自然数  前に
前に  。 これらのペアは、さらに使用するためにコンパレータの配列に書き込まれます。
。 これらのペアは、さらに使用するためにコンパレータの配列に書き込まれます。
関数BおよびSのソースコード
以下では、次の規則に従ってCコードの例を示します。
githubで強調表示されている通常の構文の関数コード。
- タイプTの配列は、配列(T)として示されます。
- 配列を操作するためのすべての関数は、ある種のarray.hで定義され、名前に書かれているとおりに実行されると考えています。
- array_push()関数に加えて、ベクトルの場合、渡された値を配列の最後に追加し、必要に応じてメモリを割り当てます。 通常の配列の場合-最後に書き込まれた後、渡された値をゼロから書き込みます。
void S(array(int) procs_up, array(int) procs_down) { int proc_count = array_size(procs_up) + array_size(procs_down); if (proc_count == 1) { return; } else if (proc_count == 2) { array_push(&comparators, ((pair_t){ procs_up[0], procs_down[0] })); return; } array(int) procs_up_odd = array_new(array_size(procs_up) / 2 + array_size(procs_up) % 2, int); array(int) procs_down_odd = array_new(array_size(procs_down) / 2 + array_size(procs_down) % 2, int); array(int) procs_up_even = array_new(array_size(procs_up) / 2, int); array(int) procs_down_even = array_new(array_size(procs_down) / 2, int); array(int) procs_result = array_new(array_size(procs_up) + array_size(procs_down), int); for (int i = 0; i < array_size(procs_up); i++) { if (i % 2) { array_push(&procs_up_even, procs_up[i]); } else { array_push(&procs_up_odd, procs_up[i]); } } for (int i = 0; i < array_size(procs_down); i++) { if (i % 2) { array_push(&procs_down_even, procs_down[i]); } else { array_push(&procs_down_odd, procs_down[i]); } } S(procs_up_odd, procs_down_odd); S(procs_up_even, procs_down_even); array_concatenate(&procs_result, procs_up, procs_down); for (int i = 1; i + 1 < array_size(procs_result); i += 2) { array_push(&comparators, ((pair_t){ procs_result[i], procs_result[i + 1] })); } array_delete(&procs_up_odd); array_delete(&procs_down_odd); array_delete(&procs_up_even); array_delete(&procs_down_even); array_delete(&procs_result); } void B(array(int) procs) { if (array_size(procs) == 1) { return; } array(int) procs_up = array_new(array_size(procs) / 2, int); array(int) procs_down = array_new(array_size(procs) / 2 + array_size(procs) % 2, int); array_copy(procs_up, procs, 0, array_size(procs_up)); array_copy(procs_down, procs, array_size(procs_up), array_size(procs_down)); B(procs_up); B(procs_down); S(procs_up, procs_down); array_delete(&procs_up); array_delete(&procs_down); }
githubで強調表示されている通常の構文の関数コード。
以下に例を示します。
最初の例。
以下の図2は、関数Bの呼び出しの結果として形成された6つの要素の配列をソートするためのネットワークを示しています(
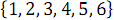 )
)
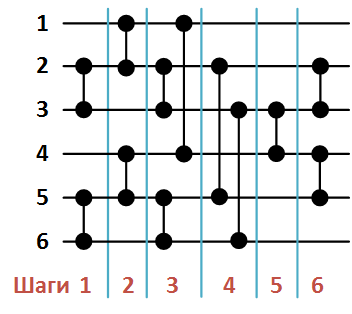
図2. 6つの要素の配列をソートするBatcherネットワーク
関数Sによる構成の順序でのコンパレータのリストは次のとおりです。
- (2、3)、
- (1、2)、
- (2、3)、
- (5、6)、
- (4、5)、
- (5、6)、
- (1、4)、
- (3、6)、
- (3、4)、
- (2、5)、
- (2、3)、
- (4、5)。
2番目の例。
2つの順序付けられた配列を組み合わせる例を考えてみましょう。
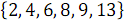 そして
そして 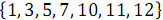 。 次の図3では、垂直ブロックは、奇数列と偶数列の配列文字列を処理するマージネットワークを示しています。
。 次の図3では、垂直ブロックは、奇数列と偶数列の配列文字列を処理するマージネットワークを示しています。
奇数の要素を組み合わせた結果として
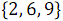 そして
そして 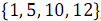 、順序付き配列が受信されます
、順序付き配列が受信されます 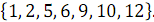 。
。
要素を偶数と組み合わせた結果
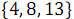 そして
そして  、順序付き配列が受信されます
、順序付き配列が受信されます 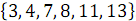 。
。
コンパレータの最後のグループの結果として、完全にソートされた配列が取得されます。
 。
。
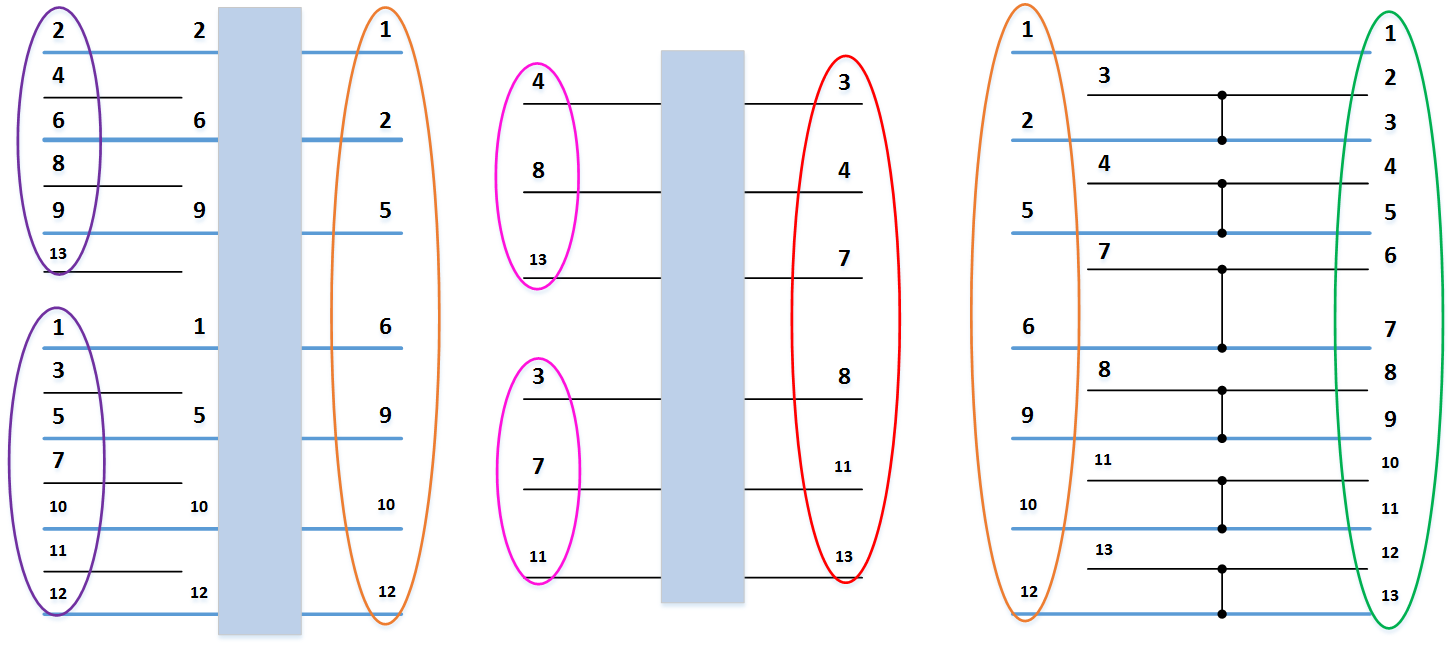
図3.ブッチャーの奇偶合併ネットワーク。
大きな配列の並べ替え
アレイのサイズがプロセッサの数を超える場合
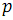 、各プロセッサに保存します
、各プロセッサに保存します 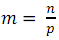 配列要素。 2段階に分類します。
配列要素。 2段階に分類します。
- 各プロセッサアレイの長さで並べ替え
 。 各プロセッサは、他のプロセッサとは独立して、配列の要素を配置するプロセスを実行します。 ソートは、利用可能な最高の順次アルゴリズムによって実行されます。
。 各プロセッサは、他のプロセッサとは独立して、配列の要素を配置するプロセスを実行します。 ソートは、利用可能な最高の順次アルゴリズムによって実行されます。 - 使用されるソートネットワークで指定されたスケジュールに従って、ソートされた各配列をマージします
 要素、つまりこの段階で、グローバルソートが実行されます。
要素、つまりこの段階で、グローバルソートが実行されます。
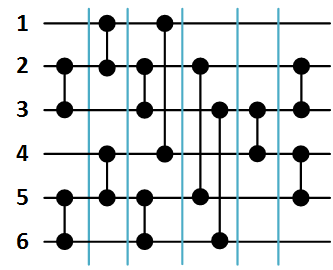
第2段階をより詳細に検討してください。 下の図4では、各データ行が1つのプロセッサに対応し、各コンパレーターがマージコンパレーターに対応しています。
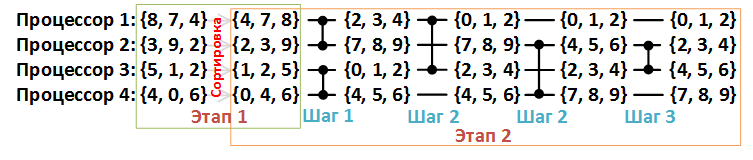
図4.配列の並べ替えの例{8、7、4、3、9、2、5、1、2、4、0、6}、n = 12、p = 4。
マージコンパレータは、入力と同じ長さの2つの配列を取得し、最初の要素に小さい値の要素が含まれ、2番目の要素に大きい値の要素が含まれるように、要素を2つの新しい配列に再分配します。
分散メモリを使用する場合、プロセッサ間でデータを転送するステップが追加されます。
- 各プロセッサは、配列の独自のフラグメントを、コンパレータの別の入力に接続されたプロセッサに送信します。
- 番号の小さいプロセッサは2つのフラグメントと区別されます
 最小要素、および多数のプロセッサ-
最小要素、および多数のプロセッサ- 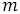 最大の要素。
最大の要素。
必要に応じて、配列にダミーのゼロ要素を追加して、ソートされたプロセッサの長さがプロセッサ数の倍数になるようにします。
したがって、最初の段階は次のように記述できます。
最初の段階のソースコード
簡単にするために、組み込みのqsort()ソート関数を使用します。 各プロセッサのソートされた配列のサイズは、次のように定義されます。
次に、最初の段階は1行のコードのみで構成されます。
githubで。
int proc_count; // int elems_count; // int elems_count_new = elems_count + (elems_count % proc_count ? proc_count - elems_count % proc_count : 0); int elems_per_proc_count = elems_count_new / proc_count;
次に、最初の段階は1行のコードのみで構成されます。
qsort(elems_result, elems_per_proc_count, array_item_size(elems_result), compare_uint32);
githubで。
2番目:
第二段階のソースコード
すでに述べたように、この段階は、コンパレーターの配列から各コンパレーターを順次処理することで構成されます。 コンパレーターの最初の入力からのプロセッサーは、その配列を2番目の入力に送信します。他のプロセッサーは同じことを行います。その結果、各プロセッサーは2つの配列を持ちます。
次に、3番目の配列( elems_temp )が各プロセッサー上に形成され、最小要素(最初のプロセッサーの場合)または最大要素(2番目のプロセッサーの場合)で構成されます。
その後、 elems_temp配列がelems_result配列の場所に書き込まれます。
githubで。
次に、3番目の配列( elems_temp )が各プロセッサー上に形成され、最小要素(最初のプロセッサーの場合)または最大要素(2番目のプロセッサーの場合)で構成されます。
その後、 elems_temp配列がelems_result配列の場所に書き込まれます。
for (int i = 0; i < array_size(comparators); i++) { pair_t comparator = comparators[i]; if (rank == comparator.a) { MPI_Send(elems_result, elems_per_proc_count, MPI_UNSIGNED, comparator.b, 0, MPI_COMM_WORLD); MPI_Recv(elems_current, elems_per_proc_count, MPI_UNSIGNED, comparator.b, 0, MPI_COMM_WORLD, &status); for (int res_index = 0, cur_index = 0, tmp_index = 0; tmp_index < elems_per_proc_count; tmp_index++) { uint32_t result = elems_result[res_index]; uint32_t current = elems_current[cur_index]; if (result < current) { elems_temp[tmp_index] = result; res_index++; } else { elems_temp[tmp_index] = current; cur_index++; } } swap_ptr(&elems_result, &elems_temp); } else if (rank == comparator.b) { MPI_Recv(elems_current, elems_per_proc_count, MPI_UNSIGNED, comparator.a, 0, MPI_COMM_WORLD, &status); MPI_Send(elems_result, elems_per_proc_count, MPI_UNSIGNED, comparator.a, 0, MPI_COMM_WORLD); int start = elems_per_proc_count - 1; for (int res_index = start, cur_index = start, tmp_index = start; tmp_index >= 0; tmp_index--) { uint32_t result = elems_result[res_index]; uint32_t current = elems_current[cur_index]; if (result > current) { elems_temp[tmp_index] = result; res_index--; } else { elems_temp[tmp_index] = current; cur_index--; } } swap_ptr(&elems_result, &elems_temp); } }
githubで。
I / O機能
入力には、 MPI_File_read_ordered()関数を使用します。この関数は、各プロセッサーのファイルから配列の等しいフラグメントを順番に読み取ります。 ファイルのデータが不十分な場合、配列を初期化したダミーのゼロは上書きされません。
出力には、同様の関数MPI_File_write_ordered()を使用しますが、各プロセッサーについて、ファイルに書き込む要素の数を計算する必要があります。 ソートされた配列の長さがプロセッサーの数の倍数でない場合、このような必要が生じます。
さらに詳しく考えてみましょう。
出力ソースコード
その考え方は次のとおりです。 プロセッサごとに3つの要素( elems_per_proc_count変数)の15個の要素の配列があると仮定します(下の図5)。 最初の5つの要素をスキップする必要があります(変数をスキップ )。

図5.プロセッサー間でのアレイの分散の例。 青で囲まれた要素を表示する必要があります。
各プロセッサについて、出力を開始する配列の先頭からのオフセット( print_offset変数)と、 印刷する要素の数( print_count変数)を計算します。
3つのケースが考えられます。
オフセットの計算を検討してください。 スキップされたアイテムの数で終わるプロセッサを除き、明らかにオフセットは常にゼロです。 そのようなプロセッサーの数は、 スキップされたelems_per_proc_countに対する比率と、小数部が破棄された比率、およびこの比率で除算の残りとしてこのプロセッサーに出力する必要のない要素の数として計算されます。
したがって、すべての条件をグループ化した後、 print_offsetの式を取得します。
以下のコードを使用すると、要素の数を計算するための式を簡単に計算できます。
githubで。

図5.プロセッサー間でのアレイの分散の例。 青で囲まれた要素を表示する必要があります。
各プロセッサについて、出力を開始する配列の先頭からのオフセット( print_offset変数)と、 印刷する要素の数( print_count変数)を計算します。
3つのケースが考えられます。
- プロセッサは何も出力しません。つまり、オフセットはゼロで、 出力の数はゼロです。
- プロセッサはその要素の一部を表示します。つまり、オフセットはスキップする要素の数であり、出力の数はelems_per_proc_countとオフセットの差です。
- プロセッサは配列内のすべての要素を表示します。つまり、オフセットはゼロで、 出力の数はelems_per_proc_countです。
オフセットの計算を検討してください。 スキップされたアイテムの数で終わるプロセッサを除き、明らかにオフセットは常にゼロです。 そのようなプロセッサーの数は、 スキップされたelems_per_proc_countに対する比率と、小数部が破棄された比率、およびこの比率で除算の残りとしてこのプロセッサーに出力する必要のない要素の数として計算されます。
したがって、すべての条件をグループ化した後、 print_offsetの式を取得します。
以下のコードを使用すると、要素の数を計算するための式を簡単に計算できます。
// , . int skip = elems_count_new - elems_count; // , . int print_offset = (skip / elems_per_proc_count == rank) * (skip % elems_per_proc_count); // . int print_count = (skip / elems_per_proc_count <= rank) * elems_per_proc_count - print_offset; // 0. MPI_File_write_ordered(output, &elems_count, rank == 0, MPI_UNSIGNED, &status); // . MPI_File_write_ordered(output, (unsigned char *)elems_result + print_offset * array_item_size(elems_result), print_count, MPI_UNSIGNED, &status);
githubで。
32ビットアプリケーションのテスト
異なる要素数のランダムな符号なし整数を含むファイルが生成された後、プログラムの結果が、標準のqsort()関数を使用して取得された標準的な回答と比較されました。
次の表では、シーケンシャルアルゴリズムの速度と、異なる数のプロセッサでのブッチャーソートを比較しています。
固定マシン(Intel Core i7-3770(4コア、8スレッド)、8 GB RAM):
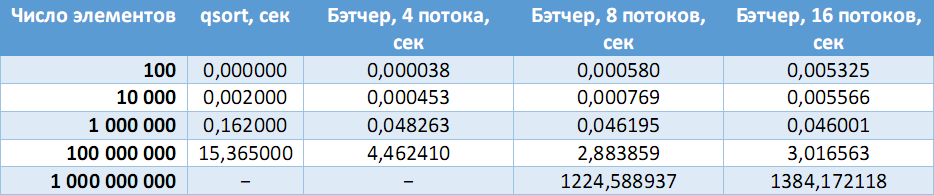
(ダッシュ-必要なメモリ量の割り当てエラー)。
ソースコード
この種類のソースコードは、GitHubのリンクhttps://github.com/zodinyac/batcher-sortから入手できます 。 README.mdで説明されているテストジェネレーターおよびその他の補助ユーティリティがあります。
中古文学
- Yakobovsky M.V.大量のデータをソートするための並列アルゴリズム。
- Yakobovsky M.V.問題を解決するための並列手法の紹介。
- Tyutlyaeva E.O. Butcher並列ソートアルゴリズムとアクティブデータストレージシステムの統合。