IEEE754の代替

IEEE754規格の機能を熟考した結果、この規格の基になっている規定の多くは誤った方法論的アプローチに基づいているという結論に達しました。 つまり、標準の作成者は推論の基礎として機械語の所定の形式を採用しました。 次に、所定の形式に基づいて、この形式で表現できる一連の数値の要件が策定されました。 多数の未確認の判断が下されました。 たとえば、コンピューターの算術演算で小数仮数を使用する場合の設定について。 または、異常な形式で数値を表現する場合の正確性の強制的な損失、および指数形式での実数のあいまいな表現の許容不能について。



したがって、各算術演算後の数値の義務的な正規化の要件が生まれ、その結果、ゼロに近い数値の表現に関する大きな問題と、明示的な形式でゼロを取得することが不可能になります。 これはすべて、正規化のためのコンピューティングリソースの不当な費用につながり、その結果との闘いにつながります。



ここで提供される作業は、Habréに関する私の2つのトピックの論理的な継続です。 私の推論では、数字の自然な表現と、数字が書かれている媒体の有限性のために、数字に適用される制限から自分自身を押し進めました。 このアプローチにより、多くの非常に重要な結論に至りました。 主なものは、算術演算のすべての段階で正規化プロセスが必須ではないということです。 さらに、特別なクラスの非正規化数を導入する必要が生じたのは必須の正規化であり、ハードウェアとソフトウェアのコストが大幅に増加しました。



提案されたアプローチにより、機械語にカテゴリを1つだけ追加することにより、 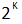時間は、浮動小数点形式で表現可能な数値の範囲を拡張します。ここで、Kはマシン仮数の桁数です。



この記事では、マシンコードでの浮動小数点数の表現を改めて見直すことができる、重要な結論を多数見つけることができます。