2つのセグメントの交差を決定する別のアルゴリズム

最近、 「2つのセグメントの交差を決定するための簡単なアルゴリズム」という出版物がありました。 2つのセグメントを少しずつ、より幾何学的に交差させる問題を解決することにしました。



2つのセグメントの交点を見つける。



2つのセグメント{P0、P1}および{P2、P3}があります。P0、P1、P2、P3は平面内の点です。 点Pのxy座標をPxおよびPyとして表します

ポイント（x float、y float）構造のP（0..3）配列に4つのポイントの座標があります。







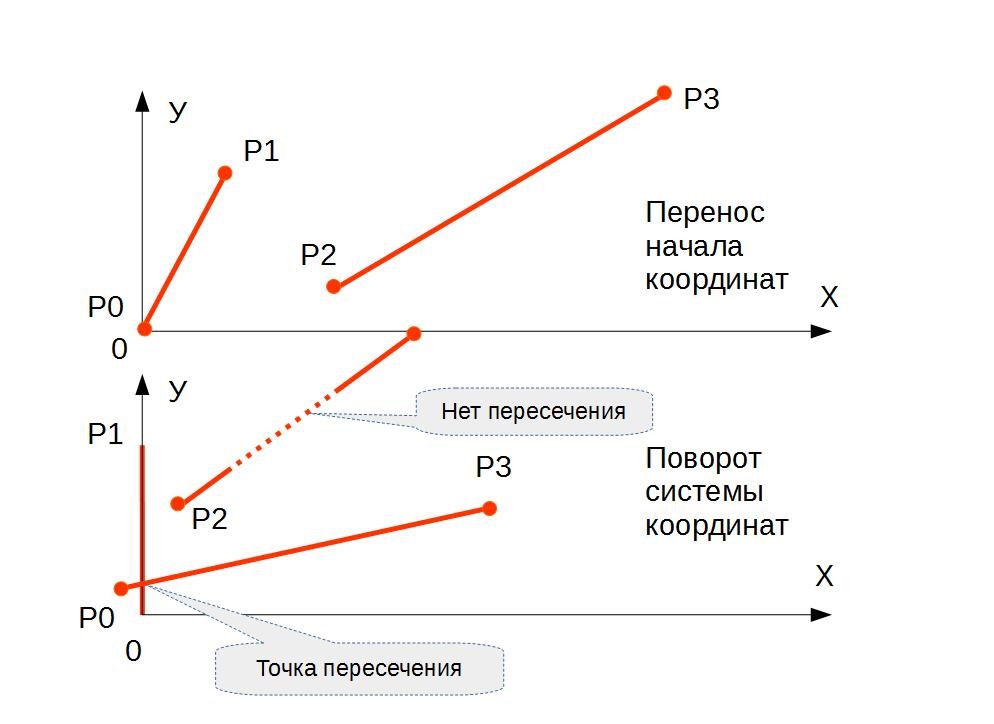
ステップ1-オリジンを転送します。



追加の配列P_copyの点Pの座標を覚えておいてください。 座標系の原点をポイントP0に転送し、ポイントの座標を再計算します。

P_copy = P P(0).x = 0 ; P(0).y = 0 for ii = 1 to 3 P(ii).x = P(ii).x - P_copy(1).x ; P(ii).y = P(ii).y - P_copy(1).y next
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ2-原点の回転

セグメント{P0、P1}が垂直位置（Y軸上にある）になるように座標系を回転します。 セグメントの長さ{P0、P1}を次のように計算します。

L1 = SQRT ( (P(1).x)^2 + (P(1).y)^2 )







座標軸の回転角の正弦と余弦：

   L1 > 0 sin_alf = sin(alfa) = P(1).x / L1 cos_alf = cos(alfa) = P(1).y / L1  L1 = 0 //    sin_alf = 0 cos_alf = 1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでも、ポイントP1、P2、P3の座標を再計算します。

  P(0).x = 0 ; P(0).y = 0 //  P0  ,     P(1).x = 0 ; P(1).y = L1 P(2).x = P(2).x * cos_alf - P(2).y * sin_alf P(2).y = P(2).y * cos_alf + P(2).x * sin_alf P(3).x = P(3).x * cos_alf - P(3).y * sin_alf P(3).y = P(3).y * cos_alf + P(3).x * sin_alf
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ3-セグメントの交点を検索します。



セグメント{P2、P3}の方程式を書き、Y軸との交点CRを見つけます。



P23X = P(2).x + ( P(3).x - P(2).x ) * beta







P23Y = P(2).y + ( P(3).y - P(2).y ) * beta







ここで、0 <= beta <= 1



セグメント{P2、P3}とY軸の交差点CRで：

P(2).x + ( P(3).x - P(2).x ) * beta =0







P（3）.x-P（2）.xの値に応じて、さらに2つのオプションが可能です。



1つのオプション：

   ( P(2).x - P(3).x ) <> 0 //  {P2,P3}   beta = P(2).x / ( P(2).x - P(3).x )  beta >= 0  beta <= 1 //  {P2,P3}   Y CR.x = 0 CR.y = P(2).y + ( P(3).y - P(2).y ) * beta //  : 0 <= CR.y <= L1
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2オプション：



P（2）.x = P（3）.xの場合、これはセグメント{P2、P3}が垂直であり、セグメント{P0、P1}に平行であることを意味します。 セグメントの交差は、2番目のセグメント{P2、P3}もY軸上にあり、その端の1つが最初のセグメント{P0、P1}（またはタッチ）にあるか、セグメント{P2、P3}が{P0、P1}を覆う場合にのみ可能 結果のために必要なポイントは1つだけであると仮定します。 これはポイントP0..P3の1つになります。



条件：

  P(2).x = P(3).x = 0 //   {P2,P3}  b    Y.  //  : P(2).y >= 0  P(2).y <= L1 // P2   {P0,P1} -> CR = P_copy(2) //    P2  P(3).y >= 0  P(3).y <= L1 // P3   {P0,P1} -> CR = P_copy(3) //    P3  P(2).y < 0  P(3).y > L1 //  {P0,P1}   {P2,P3}  P(3).y < 0  P(2).y > L1 -> CR = P_copy(0) // //    P0 ( P1) )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ4



ステップ3のオプション1に従ってCR交点が見つかった場合、その座標は元の座標系に対して再計算されます。 手順1と2で保存された変数を使用します。 回転角-アルファ：

  CR.x = CR.x * cos(-alfa) + CR.y * sin(-alfa) = CR.x * cos_alf + CR.y * sin_alf CR.y = CR.y * cos(-alfa) - CR.x * sin(-alfa) = CR.y * cos_alf - CR.x * sin_alf
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

返送：

  CR.x = CR.x + P_copy(0).x CR.y = CR.y + P_copy(0).y
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ3の条件2で CR交点が見つかった場合 、座標の再カウントは必要ありません。 catの下のサンプルgolangコード。 Golang ohmちょっと手を出しただけなので、コードに優しくしてください。 コードはgolang.orgで実行できます。