現在の画像を標準と比較する従来の「エントリレベル」の手法は、画像を2次元の輝度関数（離散2次元強度マトリックス）として考慮することに基づいています。 この場合、画像間の距離またはそれらの近接度のいずれかが測定されます。



原則として、画像間の距離を計算するには、モジュールの合計または強度差の平方である式が使用されます。

d（X、Y）= SUM（X [i、j]-Y [i、j]）^ 2

2つの画像の単純な比較に加えて、1つの画像のフラグメントの位置を別の画像で検出する問題を解決する必要がある場合、すべての座標を列挙し、上記の式を使用して距離を計算する古典的な「エントリレベル」方法は、通常、必要な数が多いために実用に失敗しますコンピューティング。



計算数を大幅に削減できる方法の1つは、フーリエ変換と離散フーリエ変換を使用して、2つの画像間の異なる変位での一致の測定値を計算することです。 この場合の計算は、互いに対する画像シフトのさまざまな組み合わせに対して同時に行われます。



（高速バージョンのさまざまなバージョンで）フーリエ変換を実装する多数のライブラリが存在するため、画像比較アルゴリズムの実装はプログラミングにとってそれほど難しくありません。

問題の声明

• 2つの画像XとYが与えられたとしましょう-それぞれサイズ（N1、N2）と（M1、M2）の画像とサンプル、そしてNi> Mi
• 完全な画像XでサンプルYの座標を見つけ、推定値（近接性の尺度）を計算する必要があります。

たとえば、次を見つけます。

サンプル

画像で

画像間の尺度としての相関

定義によれば、2つの関数FとGの相関<F、G>は量です：

<F、G> = SUM F（i）* G（i）

この値は、スカラー積と呼ばれる線形空間専用の数学および幾何学のコースでよく知られています。 式を画像間の尺度として使用します。

m（X、Y）= SUM（X [i、j] * Y [i、j]）/（SQRT（SUM X [i、j] ^ 2）* SQRT（SUM Y [i、j] ^ 2） ）

または

m（X、Y）= <X、Y> /（SQRT（<X、X>）* SQRT（<Y、Y>））

この値は、ベクトルのスカラー積演算から取得されます（画像を多次元空間のベクトルと見なします）。 さらに-同じ式は、2つの確率分布の一致の仮説の基準の標準統計式を表します。



注：

画像の断片間の相関を計算するときに、1つの画像が他の画像よりも小さい場合、交差する部分のノルムの値で除算します。

2つの関数の畳み込み

定義により、2つの関数FとGの畳み込みは関数FxGです。

FG（t）= SUM F（i）* G（j）| i + j = t

G '（t）= G（-t）およびF'（t）= F（-t）とすると、等式は明らかです。

• FF '（0）= SUM F（i）^ 2-ベクトルF自体のスカラー積
• GG '（0）= SUM G（j）^ 2–ベクトルG自体のスカラー積
• FG '（0）= SUM F（i）* G（i）-2つのベクトルFとGのスカラー積

また、FxG '（t）は、ステップtで1つのベクトルを別のベクトルに対してシフトすることによって得られる相関に等しいことも明らかです（これは、相関式の値を明示的に置き換えることで簡単に検証できます）。

フーリエ変換

フーリエ変換（ℱ）は、実変数の1つの関数を別の関数（実変数）にマッピングする演算です。 この新しい関数は、元の関数を基本成分（異なる周波数の調和振動）に分解する際の係数（「振幅」）を記述します。



実変数の関数fのフーリエ変換は積分であり、次の式で与えられます。







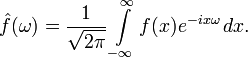
異なるソースは、整数の前の係数と指数の「-」記号を選択することにより、上記のものとは異なる定義を与える場合があります。 ただし、一部の数式の外観は変わる可能性がありますが、すべてのプロパティは同じです。



さらに、この概念にはさまざまな一般化があります。

多次元フーリエ変換

空間ℝ^ nで定義された関数のフーリエ変換は、式によって決定されます。







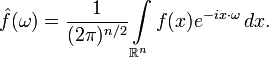
この場合の逆変換は次の式で与えられます。







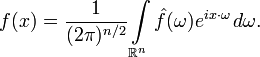
前と同じように、異なるソースでは、多次元フーリエ変換の定義は、積分の前の定数の選択が異なる場合があります。

離散フーリエ変換

離散フーリエ変換（英国文学DFT、離散フーリエ変換）は、デジタル信号処理アルゴリズム（その変更はMP3へのオーディオ圧縮、JPEGでの画像圧縮など）で広く使用されているフーリエ変換の1つです。離散（たとえば、デジタル化されたアナログ）信号の周波数分析に関連する領域。 離散フーリエ変換には、入力として離散関数が必要です。 このような関数は、多くの場合、離散化（連続関数からの値のサンプリング）によって作成されます。 離散フーリエ変換は、偏微分方程式を解き、畳み込みなどの演算を実行するのに役立ちます。 離散フーリエ変換は、時系列の分析の統計でも積極的に使用されます。 多次元離散フーリエ変換があります。

離散変換式

直接変換：







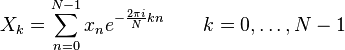
逆変換：







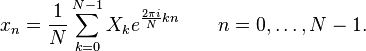
離散フーリエ変換は、時間サンプルのベクトルを同じ長さのスペクトルサンプルのベクトルに変換する線形変換です。 したがって、変換は、対称正方行列にベクトルを乗算することで実装できます。

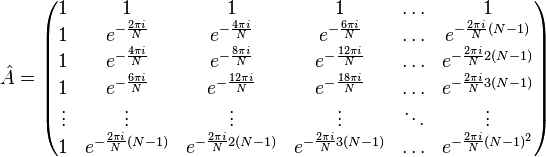
畳み込み計算のためのフーリエ変換

フーリエ変換の注目すべき特性の1つは、定義された2つの関数の相関を、実引数（古典的な式を使用する場合）または有限リング（離散変換を使用する場合）で迅速に計算できることです。



同様の特性は多くの線形変換に固有のものですが、実際の使用では畳み込み演算を計算するために、定義に従って式が使用されます

FxG = BFT（FFT（F）* FFT（G））

どこで

• FFT-直接フーリエ変換操作
• BFT-逆フーリエ変換操作

フーリエ変換式を明示的に置き換えて、結果の式を減らすことにより、等価性の正当性を検証することは非常に簡単です

相関を計算するためのフーリエ変換

<F、G>（t）を、あるベクトルを別のベクトルに対してステップtだけシフトした結果として得られた相関と等しくする

次に、すでに示したように、

<F、G>（t）= FxG '（t）= BFT（FFT（F）* FFT（G'））

複素数によるフーリエ変換アルゴリズムの実装が使用される場合、そのような変換にはもう1つの注目すべき特性があります。

FFT（G '）=共役（FFT（G））

CONJUGATE（FFT（G））は、マトリックスFFT（G）の共役要素で構成されるマトリックスです。

したがって、

<F、G>（t）= BFT（FFT（F）*共役（FFT（G）））

問題を解決するためのフーリエ変換

相互に（i、j）をシフトするときに画像間の距離を推定する式を使用する場合

m（X、Y）（i、j）= <X、Y>（i、j）/（| X |（i、j））* | Y |（i、j））、

私たちはそれを得る

• <X、Y> = XxY '= BFT（FFT（X）*共役（FFT（Y）））
• | X | ^ 2 = <X、X> = XxX'xE '= BFT（FFT（X）*コンジュゲート（FFT（X））*コンジュゲート（FFT（E）））= BFT（SQUAREMAGNITUDE（FFT（X））） *共役（FFT（E）））
• | Y | ^ 2 = <Y、Y> = YxY'xE '= BFT（FFT（Y）*コンジュゲート（FFT（Y））*コンジュゲート（FFT（E）））

どこで

• <X、Y>（i、j）-相互の画像XおよびYに対して（i、j）をシフトすることにより得られた2つの画像のスカラー積
• Eは、XとYの最小寸法に等しいサイズの画像で、単位値で埋められます（つまり、XとYが比較される「フレーム」）
• | X |（i、j）は、シフト（i、j）の下の画像Xの一般部分のノルムです。
• | Y |（i、j）は、（i、j）をシフトするときのイメージYの共通部分のノルムです。
• FFT-直接2次元離散フーリエ変換の操作
• BFT-逆2次元離散フーリエ変換の操作
• CONJUGATE-共役要素の行列を計算する操作
• SQUAREMAGNITUDE–要素振幅の二乗行列を計算する操作

問題を解決するための式の簡素化

1つのサンプルを検索する問題を解決する場合、サンプルの追加の正規化は不要であり、共通部分のノルムの計算は、この共通部分のピクセルの輝度の合計またはこの共通部分の輝度の2乗の合計で置き換えることができます。

相互に（i、j）をシフトするときに画像間の距離を推定する式を使用する場合

m（X、Y）（i、j）= <X、Y>（i、j）/ | X | ^ 2（i、j）、

私たちはそれを得る

• <X、Y> = BFT（FFT（X）*共役（FFT（Y）））
• <X、X> = BFT（正方形（FFT（X））*共役（FFT（E）））

どこで

• <X、Y>（i、j）-相互の画像XおよびYに対して（i、j）をシフトすることにより得られた2つの画像のスカラー積
• Eは、XとYの最小寸法に等しいサイズの画像で、単位値で埋められます（つまり、XとYが比較される「フレーム」）
• <X、X>（i、j）は、シフト（i、j）での画像Xの全部分のノルム（ピクセルの輝度の合計）です。
• FFT-直接2次元離散フーリエ変換の操作
• BFT-逆2次元離散フーリエ変換の操作
• CONJUGATE-共役要素の行列を計算する操作
• SQUAREMAGNITUDE–要素振幅の二乗行列を計算する操作

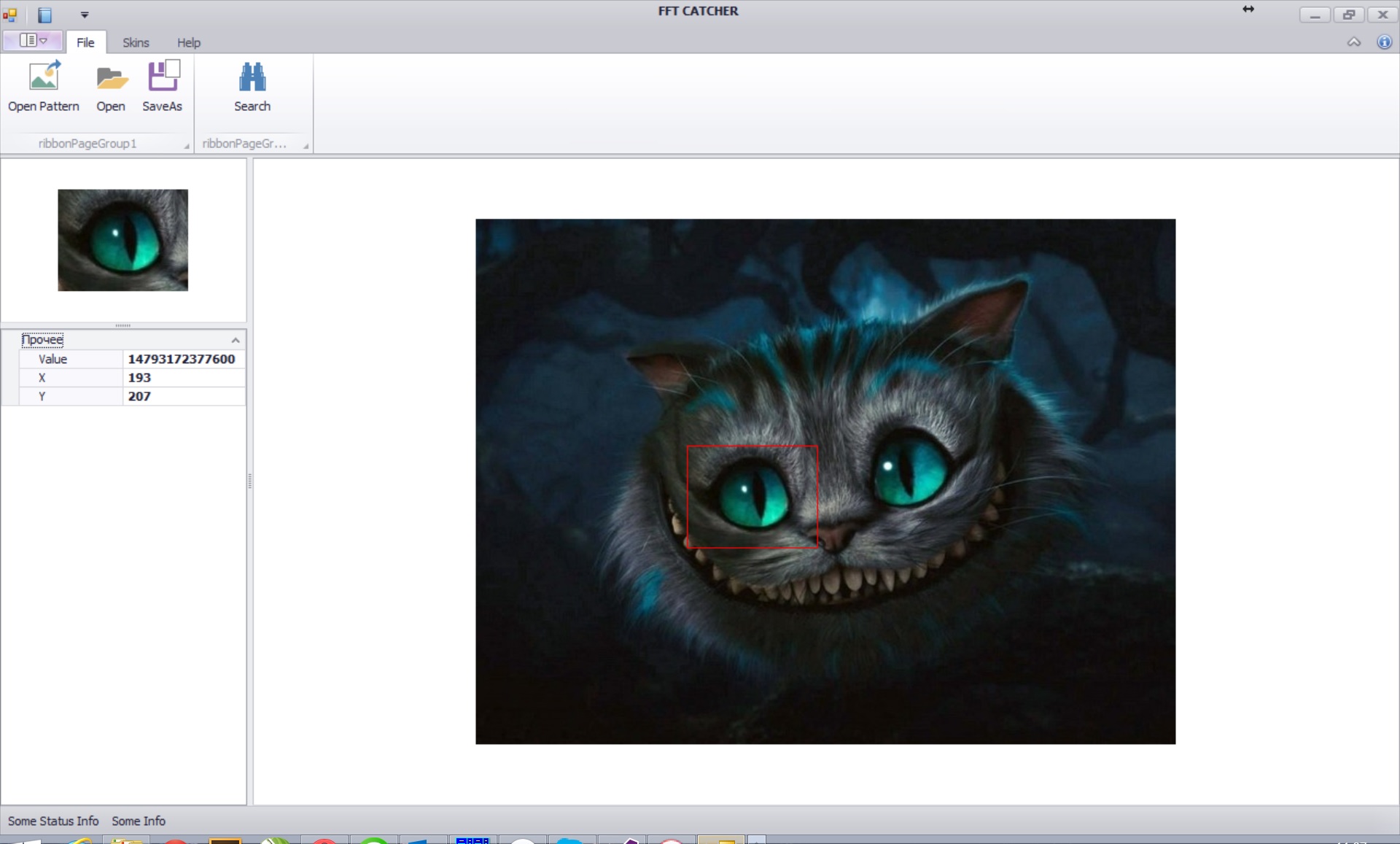
フルイメージでのフラグメント検索アルゴリズム

• 2つの画像XとYが与えられたとしましょう-それぞれサイズ（N1、N2）と（M1、M2）の画像とサンプル、そしてNi> Mi
• 完全な画像XでサンプルYの座標を見つけ、推定値（近接性の尺度）を計算する必要があります。

1. 画像Yをサイズ（N1、N2）に拡張し、ゼロでパディングします
2. サイズの単位（M1、M2）からイメージEを形成し、サイズ（N1、N2）に拡張し、それにゼロを追加します
3. 計算<X、Y> = BFT（FFT（X）* CONJUGATE（FFT（Y）））
4. 計算<X、X> = BFT（SQUAREMAGNITUDE（FFT（X））* CONJUGATE（FFT（E）））
5. 計算M [i、j] =（f + <X、Y> [i、j]）/（f + <X、X> [i、j]）
6. 行列Mで、最大値を持つ要素を見つけます。この要素の座標は、フルイメージ内のサンプルの目的の位置であり、値は比較測定の推定値に等しくなります。

注：

離散フーリエ変換を使用する場合、行列Mには、画像自体の循環シフトからの要素も含まれます。 したがって、フレームの循環シフトを分析する必要がない場合、行列Mの最大要素の検索は、領域（0,0）-（N1-M1、N2-M2）に制限する必要があります。

実装例

実装されたアルゴリズムは、オープンソースライブラリFFTToolsの一部です。 インターネットアドレス： github.com/dprotopopov/FFTTools



使用したソフトウェア

• Microsoft Visual Studio 2013 C＃-環境とプログラミング言語
• EmguCV / OpenCV-画像処理のための構造とアルゴリズムのC ++ライブラリ
• FFTWSharp / FFTW-高速離散フーリエ変換アルゴリズムを実装するC ++ライブラリ

/// <summary> /// Catch pattern bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Matrix of values</returns> private Matrix<double> Catch(Image<Gray, double> image) { const double f = 1.0; int length = image.Data.Length; int n0 = image.Data.GetLength(0); int n1 = image.Data.GetLength(1); int n2 = image.Data.GetLength(2); Debug.Assert(n2 == 1); // Allocate FFTW structures var input = new fftw_complexarray(length); var output = new fftw_complexarray(length); fftw_plan forward = fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Forward, fftw_flags.Estimate); fftw_plan backward = fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Backward, fftw_flags.Estimate); var matrix = new Matrix<double>(n0, n1); double[,,] patternData = _patternImage.Data; double[,,] imageData = image.Data; double[,] data = matrix.Data; var doubles = new double[length]; // Calculate Divisor Copy(patternData, data); Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); Complex[] complex = output.GetData_Complex(); Buffer.BlockCopy(imageData, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); input.SetData(output.GetData_Complex().Zip(complex, (x, y) => x*Complex.Conjugate(y)).ToArray()); backward.Execute(); IEnumerable<double> doubles1 = output.GetData_Complex().Select(x => x.Magnitude); if (_fastMode) { // Fast Result Buffer.BlockCopy(doubles1.ToArray(), 0, data, 0, length*sizeof (double)); return matrix; } // Calculate Divider (aka Power) input.SetData(doubles.Select(x => new Complex(x*x, 0)).ToArray()); forward.Execute(); complex = output.GetData_Complex(); CopyAndReplace(_patternImage.Data, data); Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); input.SetData(complex.Zip(output.GetData_Complex(), (x, y) => x*Complex.Conjugate(y)).ToArray()); backward.Execute(); IEnumerable<double> doubles2 = output.GetData_Complex().Select(x => x.Magnitude); // Result Buffer.BlockCopy(doubles1.Zip(doubles2, (x, y) => (f + x*x)/(f + y)).ToArray(), 0, data, 0, length*sizeof (double)); return matrix; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 /// <summary> /// Copy 3D array to 2D array (sizes can be different) /// Flip copied data /// Reduce last dimension /// </summary> /// <param name="input">Input array</param> /// <param name="output">Output array</param> private static void Copy(double[,,] input, double[,] output) { int n0 = output.GetLength(0); int n1 = output.GetLength(1); int m0 = Math.Min(n0, input.GetLength(0)); int m1 = Math.Min(n1, input.GetLength(1)); int m2 = input.GetLength(2); for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] = input[i, j, 0]; for (int k = 1; k < m2; k++) for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] += input[i, j, k]; } /// <summary> /// Copy 3D array to 2D array (sizes can be different) /// Replace items copied by value /// Flip copied data /// Reduce last dimension /// </summary> /// <param name="input">Input array</param> /// <param name="output">Output array</param> /// <param name="value">Value to replace copied data</param> private static void CopyAndReplace(double[,,] input, double[,] output, double value = 1.0) { int n0 = output.GetLength(0); int n1 = output.GetLength(1); int m0 = Math.Min(n0, input.GetLength(0)); int m1 = Math.Min(n1, input.GetLength(1)); int m2 = input.GetLength(2); for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] = value; } /// <summary> /// Find a maximum element in the matrix /// </summary> /// <param name="matrix">Matrix of values</param> /// <param name="x">Index of maximum element</param> /// <param name="y">Index of maximum element</param> /// <param name="value">Value of maximum element</param> public void Max(Matrix<double> matrix, out int x, out int y, out double value) { double[,] data = matrix.Data; int n0 = data.GetLength(0); int n1 = data.GetLength(1); value = data[0, 0]; x = y = 0; for (int i = 0; i < n0; i++) { for (int j = 0; j < n1; j++) { if (data[i, j] < value) continue; value = data[i, j]; x = j; y = i; } } } /// <summary> /// Catch pattern bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Array of values</returns> public Matrix<double> Catch(Bitmap bitmap) { using (var image = new Image<Gray, Byte>(bitmap)) return Catch(image); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

噛んだ

文学

1. A.L. ドミトリエフ。 情報処理の光学的方法。 学習ガイド。 SPb。 SPYUGUITMO 2005.46 p。
2. A.A. Akayev、S.A. Mayorov「情報処理の光学的方法」M .: 1988
3. J.グッドマン「フーリエ光学入門」M。：世界1970