unsigned long long BasicRandGenerator() { unsigned long long randomVariable; // some magic here ... return randomVariable; }
離散値を使用すると、すべてがより直感的になります。 離散ランダム変数分布関数:
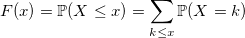
離散確率変数の分布は単純ですが、連続変数よりも生成するのが難しい場合があります。 前回同様、ささいな例から始めましょう。
ベルヌーイ分布
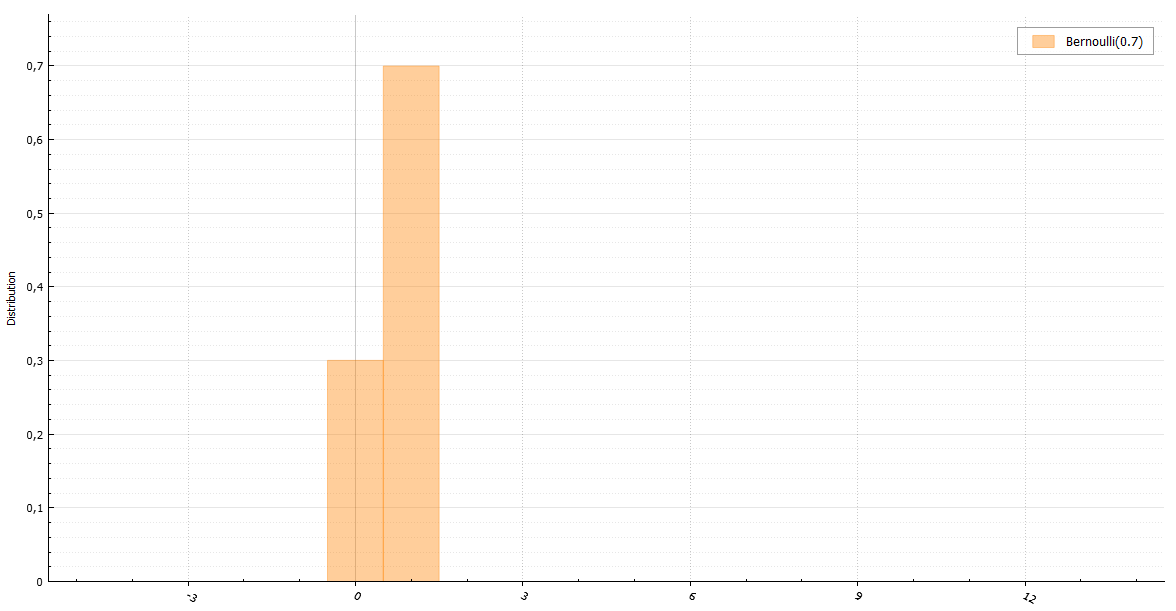
おそらく、ベルヌーイ分布でランダム変数を生成する最も速い明白な方法は、この方法で行うことです(すべてのジェネレーターは、単一のインターフェースのためにdoubleを返します)。
void setup(double p) { unsigned long long boundary = (1 - p) * RAND_MAX; // we storage this value for large sampling } double Bernoulli(double) { return BasicRandGenerator() > boundary; }
時にはそれをより速くすることができます。 「時々」とは「パラメータpが1/2のべき乗の場合」を意味します。 実際、BasicRandGenerator()関数によって返された整数が均一に分布したランダム変数である場合、そのすべてのビットが等しく分布します。 これは、バイナリ表現では、数がベルヌーイによって分散されたビットで構成されることを意味します。 これらの記事では、ベースジェネレーターの関数がunsigned long longを返すため、64ビットがあります。 p = 1/2に対してできるトリックは次のとおりです。
double Bernoulli(double) { static const char maxDecimals = 64; static char decimals = 1; static unsigned long long X = 0; if (decimals == 1) { /// refresh decimals = maxDecimals; X = BasicRandGenerator(); } else { --decimals; X >>= 1; } return X & 1; }
BasicRandGenerator()関数のランタイムが十分に短くなく、暗号の安定性とジェネレーター期間のサイズを無視できる場合、そのような場合には、ベルヌーイ分布のサンプルサイズに対して一様に分布したランダム変数を1つだけ使用するアルゴリズムがあります:
void setup(double p) { q = 1.0 - p; U = Uniform(0, 1); } double Bernoulli(double p) { if (U > q) { U -= q; U /= p; return 1.0; } U /= q; return 0.0; }
なぜこのアルゴリズムが機能するのですか? 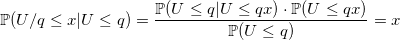
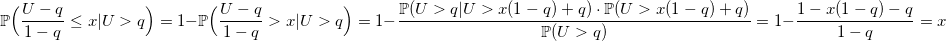
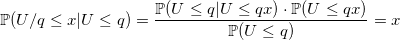
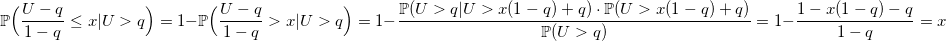
均一な分布
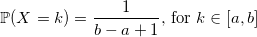
誰でも、aからbまでの彼の最初のランダムな整数ジェネレータが次のようになったことを覚えているでしょう。
double UniformDiscrete(int a, int b) { return a + rand() % (b - a + 1); }
まあ、それは正しい決断です。 常に真ではないという唯一の仮定で、優れたベースジェネレーターが得られます。 古いC-shny rand()のように欠陥がある場合、毎回奇数の後に偶数を取得します。 ジェネレーターを信頼していない場合は、次のように記述する方が適切です。
double UniformDiscrete(int a, int b) { return a + round(BasicRandGenerator() * (b - a) / RAND_MAX); }
また、RAND_MAXが区間b-a + 1の長さで完全に分割されていない場合、分布は完全に均一ではないことに注意してください。 ただし、この長さが十分に小さければ、差はそれほど大きくありません。
幾何分布


パラメーターpの幾何分布を持つ確率変数は、パラメーター-ln(1-p)の指数分布を持つ確率変数で、最も近い整数に切り捨てられます。
証明
Wを-ln(1-p)パラメーターを使用して指数関数的に分布するランダム変数とします。 次に:
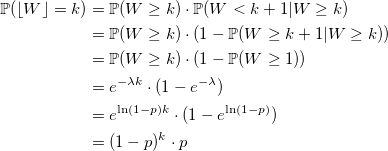
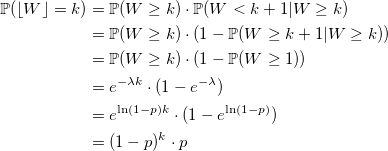
void setupRate(double p) { rate = -ln(1 - p); } double Geometric(double) { return floor(Exponential(rate)); }
より速くすることは可能ですか? 時々。 分布関数を見てみましょう。
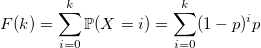
そして、通常の反転方法を使用します。標準的な一様分布のランダム変数Uを生成し、この合計がUより大きいkの最小値を返します。
double GeometricExponential(double p) { int k = 0; double sum = p, prod = p, q = 1 - p; double U = Uniform(0, 1); while (U < sum) { prod *= q; sum += prod; ++k; } return k; }
このような順次検索は、幾何分布を持つランダム変数の値がゼロ付近に集中している場合、非常に効果的です。 ただし、p値が小さすぎると、アルゴリズムの速度がすぐに失われます。この場合、指数ジェネレーターを使用することをお勧めします。
秘密があります。 p、(1-p)* p、(1-p)^ 2 * p、...の値は、事前に計算して記憶できます。 問題はどこに泊まるかです。 そして、指数関数から継承した幾何学的分布の特性であるメモリ不足がシーンに現れます。
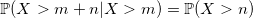
このプロパティにより、(1-p)^ i * pの最初の数個の値のみを記憶し、再帰を使用できます。
// works nice for p > 0.2 and tableSize = 16 void setupTable(double p) { table[0] = p; double prod = p, q = 1 - p; for (int i = 1; i < tableSize; ++i) { prod *= q; table[i] = table[i - 1] + prod; } } double GeometricTable(double p) { double U = Uniform(0, 1); /// handle tail by recursion if (U > table[tableSize - 1]) return tableSize + GeometricTable(p); /// handle the main body int x = 0; while (U > table[x]) ++x; return x; }
二項分布

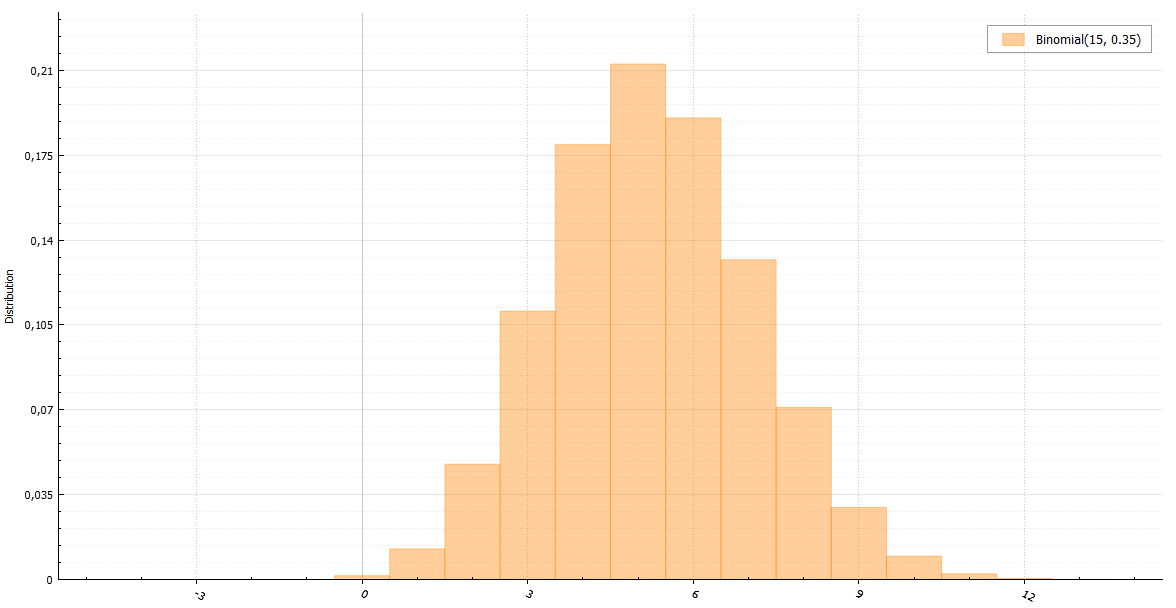
定義では、二項分布の確率変数は、ベルヌーイ分布のn個の確率変数の合計です。
double BinomialBernoulli(double p, int n) { double sum = 0; for (int i = 0; i != n; ++i) sum += Bernoulli(p); return sum; }
ただし、回避する必要があるnには線形の依存関係があります。 定理を使用できます。Y_1、Y_2、...がパラメーターpの幾何分布を持つランダム変数であり、Xが次のような最小整数の場合:
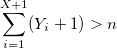
Xには二項分布があります。
証明
定義により、Yの幾何分布を持つ確率変数は、最初の成功までのベルヌーイ実験の数です。 別の定義があります:Z = Y + 1-最初の成功までのベルヌーイ実験の数。 したがって、独立したZ_iの合計は、X + 1成功までのベルヌーイ実験の数です。 そして、この合計がnよりも大きいのは、最初のn個のテストのうち、成功したテストがX個以下である場合だけです。 したがって:

qed

qed
次のコードのランタイムは、n * pの増加とともにのみ増加します。
double BinomialGeometric(double p, int n) { double X = -1, sum = 0; do { sum += Geometric(p) + 1.0; ++X; } while (sum <= n); return X; }
それでも、時間の複雑さは増大しています。
二項分布には1つの特徴があります。 nが大きくなると、正規分布になるか、p〜1 / nの場合はポアソン分布になる傾向があります。 これらの分布用のジェネレーターがあるので、そのような場合は二項ジェネレーターに置き換えることができます。 しかし、これで十分でない場合はどうでしょうか? Luc Devroyeの本、Non-Uniform Random Variate Generationには、大きなn * p値に対して同等に高速に動作するアルゴリズム例があります。 アルゴリズムの考え方は、正規分布と指数分布を使用して偏差でサンプリングすることです。 残念ながら、このアルゴリズムの操作に関する話はこの記事には大きすぎますが、指定された本では徹底的に説明されています。
ポアソン分布
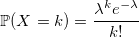
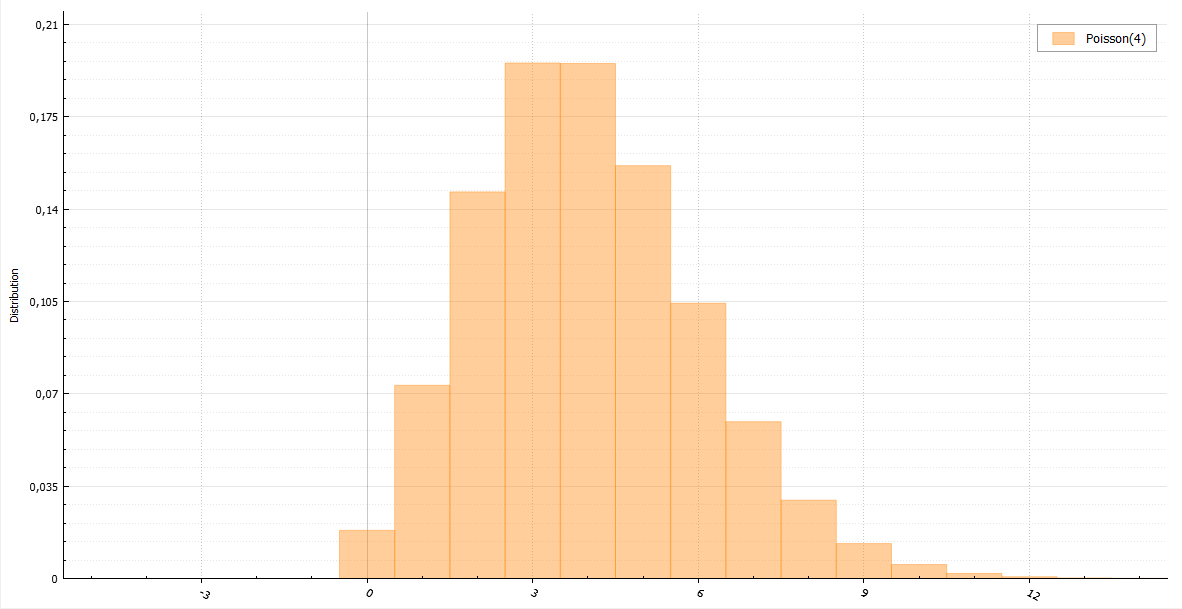
W_iが密度ラムダの標準的な指数分布の確率変数である場合、次のようになります。
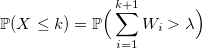
証明
f_k(y)を標準アーラン分布の密度(k個の標準的な指数分布ランダム変数の合計)とする:
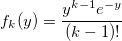
それから
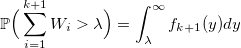
およびkを取得する確率:
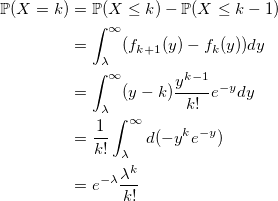
ポアソン分布と一致します。 qed
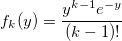
それから
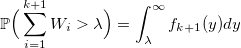
およびkを取得する確率:
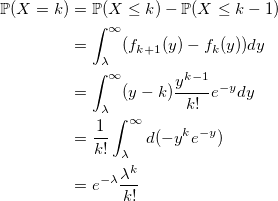
ポアソン分布と一致します。 qed
このプロパティを使用して、指数関数的に分布した量の合計を密度率で生成することができます。
double PoissonExponential(double rate) { int k = -1; double s = 0; do { s += Exponential(1); ++k; } while (s < rate); return k; }
人気のあるKnuthアルゴリズムは、このプロパティに基づいています。 指数変数の合計の代わりに、それぞれが-ln(U)を介した反転法で取得できるので、均一なランダム変数の積を使用します。

そして:

exp(-rate)の値を事前に記憶し、積がそれを超えるまでU_iを連続的に乗算します。
void setup(double rate) expRateInv = exp(-rate); } double PoissonKnuth(double) { double k = 0, prod = Uniform(0, 1); while (prod > expRateInv) { prod *= Uniform(0, 1); ++k; } return k; }
1つのランダム変数の生成と反転メソッドのみを使用できます。

このような条件を満たすkの検索は、最も可能性の高い値、つまりフロア(レート)から開始するのが最善です。 UをX <floor(rate)である確率と比較し、Uが大きい場合は上昇し、別の場合は下降します。
void setup(double rate) floorLambda = floor(rate); FFloorLambda = F(floorLamda); // P(X < floorLambda) PFloorLambda = P(floorLambda); // P(X = floorLambda) } double PoissonInversion(double) { double U = Uniform(0,1); int k = floorLambda; double s = FFloorLambda, p = PFloorLambda; if (s < U) { do { ++k; p *= lambda / k; s += p; } while (s < U); } else { s -= p; while (s > U) { p /= lambda / k; --k; s -= p; } } return k; }
3つのジェネレーターすべての問題は1つです。密度パラメーターに応じて複雑さが増します。 しかし、救いがあります-高密度の値では、ポアソン分布は正規分布になります。 上記の「非一様ランダム変量生成」の複雑なアルゴリズムを使用することもできますし、単に近似するだけで、速度の名前の精度を無視することもできます(タスクによって異なります)。
負の二項分布
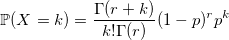
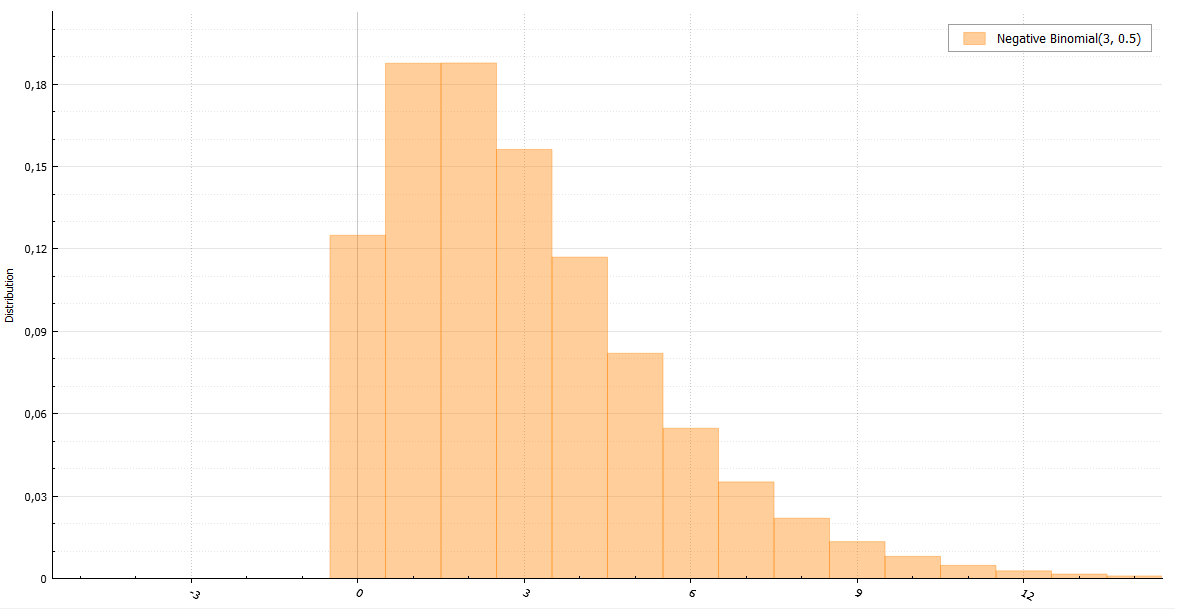
負の二項分布は、パスカル分布(rが整数の場合)およびフィールド分布(rが実数の場合)とも呼ばれます。 特性関数を使用すると、パスカル分布がパラメーター1-pのrの幾何学的分布量の合計であることを簡単に証明できます。
double Pascal(double p, int r) { double x = 0; for (int i = 0; i != r; ++i) x += Geometric(1 - p); return x; }
このようなアルゴリズムの問題は、rに対する線形依存性です。 どのパラメーターでも同等に機能するものが必要です。 そして、優れたプロパティがこれに役立ちます。 確率変数Xにポアソン分布がある場合:

密度はランダムで、ガンマ分布があります:
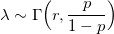
Xは負の二項分布を持ちます。 したがって、ポアソンガンマ分布と呼ばれることもあります。
証明 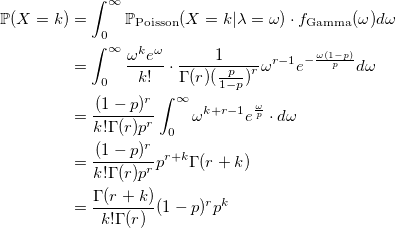
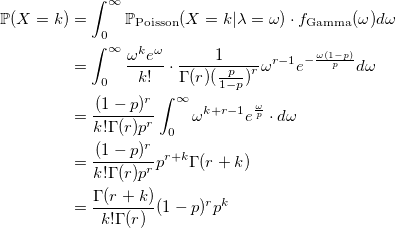
これで、パラメータrの大きな値に対してPascal分布を持つランダムジェネレーターをすばやく作成できます。
double Pascal(double p, int r) { return Poisson(Gamma(r, p / (1 - p))); }
超幾何分布
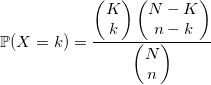
投票箱にN個のボールがあり、そのうちK個が白であると想像してください。 n個のボールを引いています。 それらの間の白の数は、超幾何分布を持ちます。 一般に、この定義を使用するアルゴリズムを使用することをお勧めします。
double HyperGeometric(int N, int n, int K) { double sum = 0, p = static_cast<double>(K) / N; for (int i = 1; i <= n; ++i) { if (Bernoulli(p) && ++sum == K) return sum; p = (K - sum) / (N - i); } return sum; }
または、パラメータ付きの二項分布による偏差のあるサンプルを使用できます。
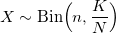
および定数M:
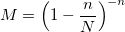
二項分布アルゴリズムは、nが大きい場合やNが大きい場合(n << Nなど)の極端な場合にうまく機能します。 それ以外の場合は、入力パラメーターの増加に伴って複雑さが増しているにもかかわらず、以前のものを使用することをお勧めします。
対数分布

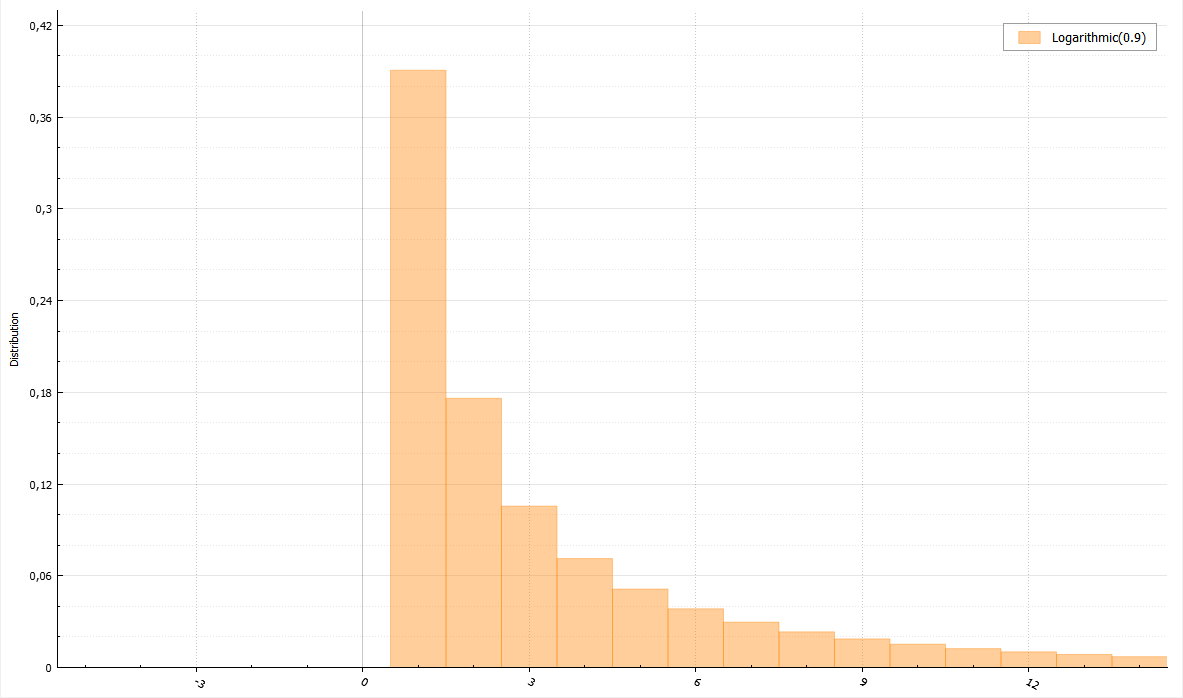
この分布には有用な定理があります。 UとVが0から1までの一様分布のランダム変数である場合、量
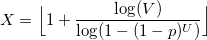
対数分布になります。
証明
指数分布と幾何分布の生成元を思い出すと、上記の式で与えられたXが次の分布を満たすことが簡単にわかります。
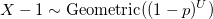
Xが対数分布を持っていることを証明しましょう:
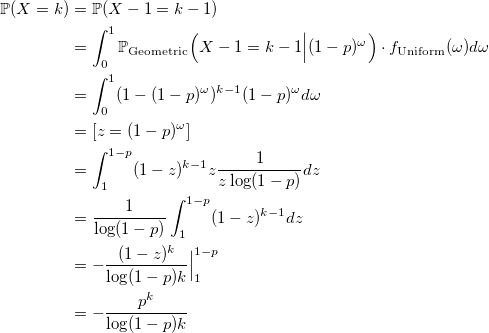
qed
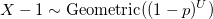
Xが対数分布を持っていることを証明しましょう:
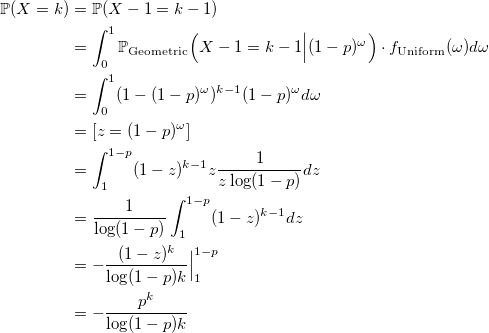
qed
アルゴリズムを高速化するには、2つのトリックを使用できます。 最初:V> pの場合、X = 1 p> = 1-(1-p)^ U 2番目:q = 1-(1-p)^ U、次にV> qの場合、X = 1、V> q ^ 2の場合、X = 2など したがって、対数を頻繁にカウントすることなく、最も可能性の高い値1と2を返すことができます。
void setup(double p) { logQInv = 1.0 / log(1.0 - p); } double Logarithmic(double p) { double V = Uniform(0, 1); if (V >= p) return 1.0; double U = Uniform(0, 1); double y = 1.0 - exp(U / logQInv); if (V > y) return 1.0; if (V <= y * y) return floor(1.0 + log(V) / log(y)); return 2.0; }
ゼータ分布
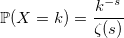
分母にはリーマンゼータ関数があります:
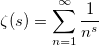
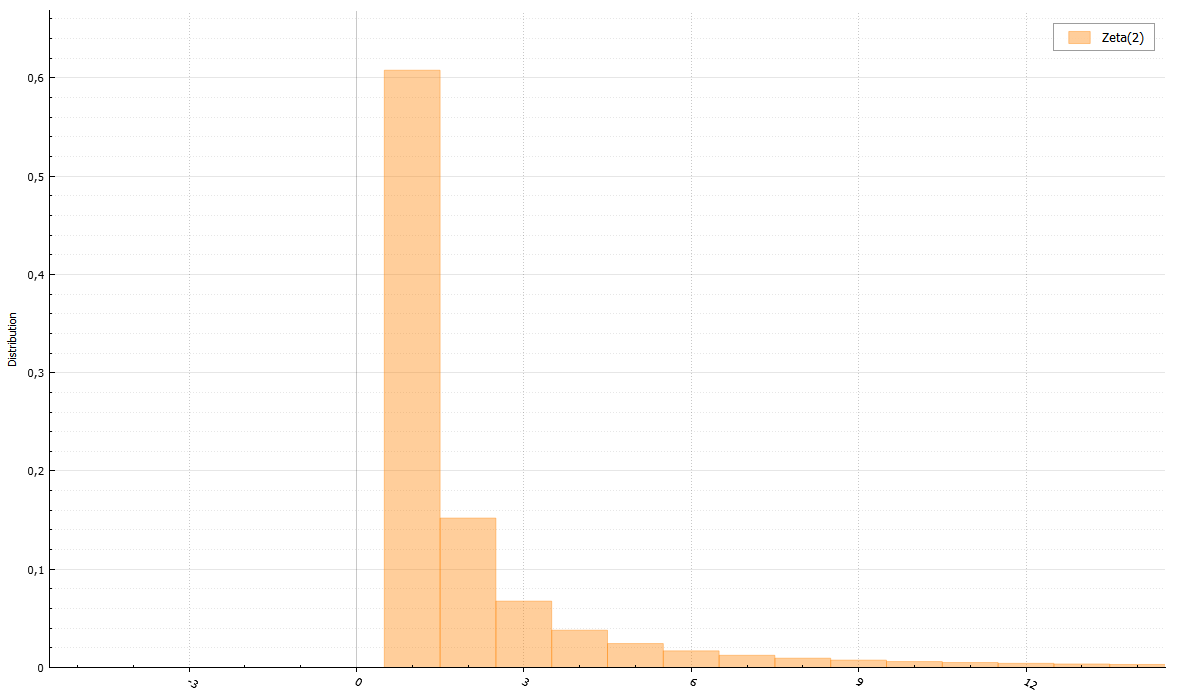
ゼータ分布には、リーマンのゼータ関数を計算しないようにするアルゴリズムがあります。 パレート分布を生成することができる必要があるだけです。 読者のリクエストに応じて証明を添付できます。
void setup(double s) { double sm1 = s - 1.0; b = 1 - pow(2.0, -sm1); } double Zeta(double) { /// rejection sampling from rounded down Pareto distribution int iter = 0; do { double X = floor(Pareto(sm1, 1.0)); double T = pow(1.0 + 1.0 / X, sm1); double V = Uniform(0, 1); if (V * X * (T - 1) <= T * b) return X; } while (++iter < 1e9); return NAN; /// doesn't work }
最後に、他の複雑な分布のための小さなアルゴリズム:
double Skellam(double m1, double m2) { return Poisson(m1) - Poisson(m2); } double Planck(double a, double b) { double G = Gamma(a + 1, 1); double Z = Zeta(a + 1) return G / (b * Z); } double Yule(double ro) { double prob = 1.0 / Pareto(ro, 1.0); return Geometric(prob) + 1; }
C ++ 17でこれらおよび他のジェネレーターを実装する