はじめに
このビデオは繰り返し実験を示しています-「子羊」の代わりに自家製のナンセンスが使用されています
これは1985年、サリュート7軌道ステーションで、宇宙飛行士V. A.ジャニベコフとV. P.サビニクからなるソユーズT-13宇宙船の乗組員が訪れた際に起こりました。多数のネットワークソース
宇宙飛行士が軌道に運ばれた貨物を開梱したとき、彼らはいわゆる「子羊」、つまり耳のついたナットを外さなければなりませんでした。 子羊の耳を打つ価値があり、彼は自分で回転します。 その後、最後まで回転してねじ付きロッドから飛び降りると、ナットは回転し続け、無重力状態で慣性で飛行します(ほぼ回転するプロペラのように)。 そのため、ウラジミール・アレクサンドロヴィッチは、耳を前方に向けて約40センチメートル飛んだ後、ナットが突然180度反転し、同じ方向に飛び続けますが、耳は後ろに向き、反対方向に回転することに気付きました。 その後、再び、40センチメートルを飛行し、ナットは再び180度の宙返りを行い、初めてなど、耳を前にして再び飛行を続けます。 Dzhanibekovは実験を繰り返し繰り返し、結果は常に繰り返されました。 一般に、無重力で飛行する回転ナットは、43センチメートルごとに鋭い180度の周期的なフリップを行います。 彼はまた、ナットの代わりに他のオブジェクト、たとえば、通常のナットが付いたプラスチシンボールを使用しようとしました。これは、一定の距離を飛んだ後、同じ突然のフリップを行いました。
これで種は十分だと思います。 実際、「ジャニベコフ効果」には異常なものは何もありません(ただし、彼は12000年ごとの地球の極の変化、およびその他の世界的な大変動を信じています)。 テンソル代数の装置と機械的運動の安定性の理論を使用して、神秘的なナットに何が起こるかを理解しようとします。
1.ナット「ラム」-質量慣性特性
図は、調査の対象を示しています。 確かに読者のそれぞれは、生涯に少なくとも一度はそのようなナットを見ました。 オリジナルとの類似性を保証することはできません、私からのアーティストは同じですが、それにもかかわらず。
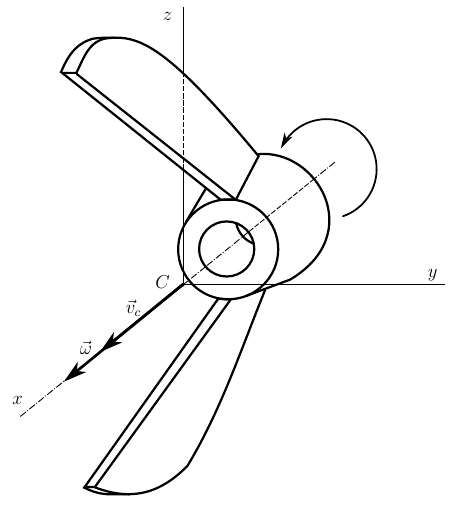
まず、ナットの動き(モデリングは計画中ですが、今のところ)定性的に勉強します。 したがって、この製品の特定の寸法には興味がありません。 このナットの形状は私たちにとって重要であり、実際には何も計算せずにいくつかの結論を引き出すことができます。
ナットは自由に動くため、重心をポールとして選択すると便利です。 さらに、適切な座標系(体に関連付けられている)をデカルト座標にし、その軸を慣性の主軸と一致させます。 このような軸は常に見つけることができ、直交します 。 これについては、 前の記事で厳密に証明しました。 したがって、中心のナット慣性テンソルは対角行列で表されると仮定できます。
明らかに、最大の主軸慣性モーメントは
そして以来
この場合、中心慣性テンソルは次の形式を取ります。
2.安定したナット運動の微分方程式
ナットはスレッドから離れると自由なボディのように移動するため、運動方程式を記述する形式は明らかです。
ナットは、地球に自由に落下する非慣性参照システム(宇宙船キャビン、無重力)で移動するため、空気抵抗がわずかであり、他の摂動を無視すると仮定して、システム(5)の右側をゼロと見なします
初期条件が与えられると、極の運動方程式は簡単に統合され、重心の均一で直線的な運動が得られます。 2番目の方程式のすべての塩も簡単に統合できます。これは、その左側が、重心に対するナットの運動量の絶対微分であるためです。
どこで
したがって、2番目の方程式は積分を与えます
MKDの不変性について語っています。 初めに角速度が厳密に軸に沿って向けられていることを考えると
3.摂動ナット運動の微分方程式
短い小さな摂動の作用下で、ナットの角速度が方程式(6)がわずかに与える法則から逸脱すると仮定します。
2番目の式(6)をテンソル形式に書き換えます
そこに置き換えます(7)
(8)の括弧を展開します
しかし
式に従って角速度の成分を再計算します
(10)を(9)に置き換えて、共通の要素を取り出します
クロネッカーデルタのプロパティを使用し、慣性テンソルのインデックスを省略すると、次のようになります。
または
どこで
結果として得られる方程式系(11)は、摂動運動の線形方程式系と呼ばれ、最初の近似で定常運動の安定性を調べるのに役立ちます。
テンソルを使用して動作することに注意してください。式(6)には、ひどい行列乗算とベクトル積さえあることを完全に忘れていました。 ベクトル行列形式の変換に対するテンソルアプローチの力の別の図。
4.最初の近似(最初のリアプノフ法)におけるヤニベコフナットの運動の安定性の研究
再び式(11)の行列形式に戻り、角速度の偏差の導関数に関してそれを解決します。
ナットの動きの安定性を評価するために使用する最初のリアプノフ法には、行列の固有値の研究が含まれます
ただし、まずはマトリックスを取得する必要があります
まず、デカルト座標で作業することを思い出してください。これは、メトリックテンソルが単位行列で表され、Levi-Civitaテンソルが既に説明したVeblenシンボルで表され、慣性テンソルがランクであることを意味します
式(13)の畳み込みには、SKAを使用できますが、MaximaとMapleのテンソルのコンポーネント単位の動作をまだ理解していないため、線形代数ツールを使用してMapleで次のコードをすばやくスケッチしました
restart; with(LinearAlgebra): # - levi_civita := proc(i, j, k) local E := IdentityMatrix(3,3); local A := Matrix(3, 3); local i1 := 0; A[1] := E[i]; A[2] := E[j]; A[3] := E[k]; return Determinant(Transpose(A)); end proc: # J := Matrix( [ [I[xx], 0, 0], [0, a*I[xx], 0], [0, 0, b*I[xx]] ]); g := IdentityMatrix(3, 3); Omega := Vector([omega, 0, 0]); L := J . Omega; # G G := Matrix(3, 3); for r from 1 to 3 do for l from 1 to 3 do G[r, l] := 0; for k from 1 to 3 do summ := 0; for m from 1 to 3 do summ := summ + levi_civita(r, k, m)*Omega[k]*J[m, l] + levi_civita(r,k,m)*g[k,l]*L[m]; end do: G[r, l] := G[r, l] + summ; end do: end do: end do:
ソースデータをMapleに渡すと、出力は行列になります
どこで
行列を取得することは難しくありません
与えられた行列の固有値を計算するための特性方程式の形式は
それを解いて固有値を取得します
次元のない慣性モーメントが条件を満たす場合、固有値は実数値を取ります
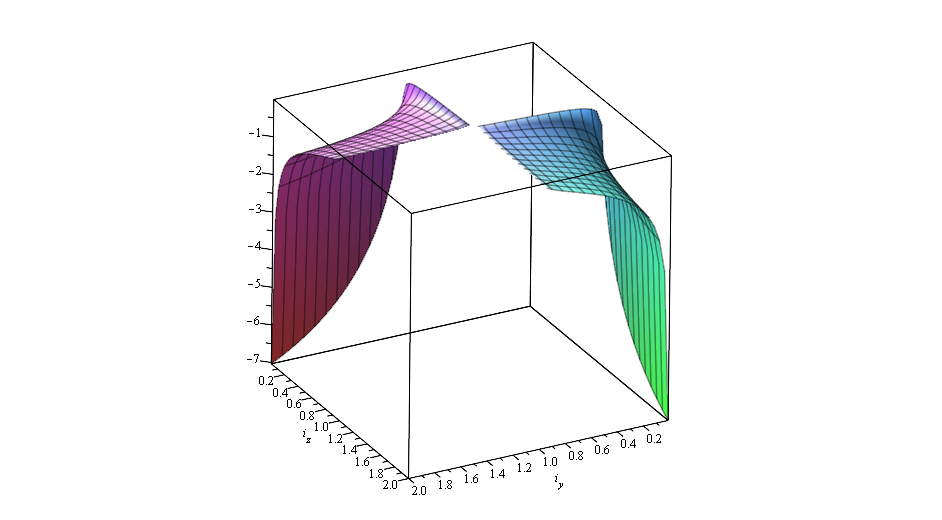
それ以外の場合、2つの固有値は純粋に虚数になります。 固有値の依存関係をプロットする場合
特性多項式の正根

特性多項式の負の根
結論
物質的な部分が正である少なくとも1つの固有値は、確立された運動レジームの不安定性を示します。
条件(15)が最初に採用した条件(3)を満たしているので、見てみましょう。 慣性モーメント間の比で、
つまり、最初は慣性モーメントの最大値と最小値の中間で軸を中心にねじれているため、ナットは不安定に動作し、反転してから再び安定した位置を見つけようとし、再び反転します。 自由体の安定した回転は、最大および最小慣性モーメントを持つ軸の周りでのみ可能であることが知られています。
もし
次に、特性方程式の純粋に虚数の根を取得します。最初のリアプノフ法は、この場合の運動が安定しているかどうかの質問に明確に答えません。 しかし、力学が今日では知らないことと、特性方程式の虚根をもつ線形方程式を解く振動性の性質から出発すると、歳差運動と章動のプロセスに対応する定常状態近くの角速度ベクトルの周期的変動を仮定することができます。
この点で、条件を満たす地球(16)は、ヤニベコフの影響を受けません。 したがって、極の変化を伴う世界的な大惨事は私たちを脅かすものではありません。
この記事はいくつかのトレーニングでした。 おそらく「子羊」の実に戻りますが、今のところは、読者の皆さんの注意に感謝します。
>継続する...