エントリー
この投稿では、友達が他の投稿を読むのを手伝いたいと思っています。 これは、プログラミング言語の理論(TNL)で使用される表記法の加速コースです。 トピックのより良い研究のために、Felleisen、Findler、およびFlattによるPLT Redexを使用したBenjamin C. PierceおよびSemantic Engineeringによる型とプログラミング言語をお勧めします。 読者は経験豊富なプログラマーであると仮定しますが、数学とTNLはそれほど優れていません。 基本的な定義から始めて、すぐに理解できるようにします。
セット、タプル、関係、およびルール定義
多くの読者はセット、タプル、および関係に精通していると思いますが、帰納的定義に精通していない場合は、以下の「ルールによる定義」というセクションをお読みください。
多くの
TNCで使用する主な構成要素は多数です。 オブジェクト(または要素)のコレクション。 たとえば、最初の3つの自然数で構成されるセット:{0、1、2}。
重要なのは、オブジェクトがセットに属しているかどうかだけです。 重複があるかどうか、またはセット内のオブジェクトの外観の順序は関係ありません。 たとえば、セット{0、2、1}、上記と同じセット。 表記εは「c」を意味します。 したがって、1∈{0、1、2}は真であり、3∈{0、1、2}は偽です。 セットには、無限の数の要素を含めることができます。 たとえば、 Nで示されるすべての自然数(負でない整数)のセット。
タプル
別のビルディングブロックはタプルです。 オブジェクトの順序付けられたコレクション。 T.O. (0、1、2)は3つの要素のタプルであり、タプル(0、2、1)とは異なります。 線形間表記t iは、タプルtのi番目(インデックスi)の要素を意味します。 たとえば、t =(0、2、1)、t 1 = 0、t 2 = 2、t 3 = 1の場合、タプルには常に有限数の要素が含まれ、通常はかなり多くの要素が含まれます。 タプルを指定するために、丸括弧の代わりに山括弧が使用される場合があります。
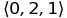 。
。
関係
タプルとセットを組み合わせると、関係が得られます。 関係は多くのタプルです。
{(0、1)、(1,2)、(2、3)、(3、4)、...}
多くの場合、入力値を週末にマッピングするために関係を使用します。 たとえば、上記の関係は、自然数からそのフォロワーへのマッピング、つまり 次に大きい自然数に。 上記の定義は(...)を使用しているため、かなり不正確です。 幸いなことに、無限のセットと関係を記述するためのより正確な表記法があります。
ルールによる定義
TNCで無限セットを定義する主な方法は、セットに含まれる要素を記述するルールのセットを提供することです。 上記のセットに名前Rを使用しましょう。 次に、次の2つのルールにより、Rの正確な定義が得られます。2番目のルールは、それ自体を参照するという意味で再帰的であることに注意してください。 これは、通常のかなり一般的な状況です。
- (0、1)∈R
- 任意の自然数nおよびmについて、(n、m)∈Rの場合、(n + 1、m + 1)∈R
ルールを使用してセットを定義する場合、これらのルールを使用してセット内のこの要素の検出を正当化する方法がない場合、セットに要素が含まれないことを意味します。 したがって、(0、0)はRに含まれません。これは、上記の規則を使用すると、(0、0)が含まれることを正当化することができないためです。
一部のルールセットは無意味であり、多くを定義していません。 たとえば、次のように、ルールは互いに矛盾しないようにする必要があります。
- (0、1)∈R
- (0、1)∉R.
TNLの教科書では、「良い」ルールセットの制限について説明していますが、これについては説明しません。 少なくとも1つのルールは非再帰的でなければならず、同様の論理的矛盾は存在しないはずです。
上記のルールの一般的な表記では、「if」と「then」の間の水平バーを使用します。 たとえば、Rの同等の定義は次のようになります。
ルール2から「正の整数nおよびmについて」を省略しました。ルールに現れるnやmなどの変数は、正しいタイプのオブジェクトで置き換えることができるという規則を使用します。 この場合、自然数。 多くの場合、「正しいタイプ」は、会話のコンテキストから推測できるものです。 この場合、自然数。
ある要素がRにあると主張するとします。(2、3)∈Rと言います。あなたは私を信じていないと答えることができます。 納得させるために、ルールが(2、3)∈Rという事実をどのように正当化するかを示す必要があります。結論を示さなければなりません。 推論は、nやmなどの変数が特定の値に置き換えられ、(n、m)∈Rなどの前提がより具体的な結論に置き換えられる一連のルールです。
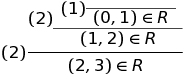
出力の各ステップにルール番号を付けました。 私が「ルール定義」と呼ぶものの仮名は帰納的定義です。
言語と文法の構文
上記で行ったように、セットを定義するためのルールの使用は、プログラミング言語の構文を定義するのにも適していることがわかります。 整数演算用の単純な言語を定義する必要があるとします。 それをアリスと呼びましょう。 1 + 3や-(5 + 2)などの式が含まれます。 Zは整数のセットであることを思い出してください。 次に、Arithを説明する多くのルールは次のようになります。
- i∈Zの場合、i∈Arithであることは事実です。
- 任意のeについて、e∈Arithの場合、-e∈Arith。
- 任意のe1およびe2について、e1∈Arithおよびe2∈Arithの場合、e1 + e2∈Arith。
- 任意のeについて、e∈Arithの場合、(e)∈Arith。
Backus-Naura Form(BNF)は、言語の構文を定義するルールを書き留めるためのもう1つの一般的な表記法であり、これは同じことを意味します。 (BNFにはいくつかのオプションがあります。ここでどれを使用するか忘れました。)ルールのセットは文法と呼ばれます。
アリス:: =整数 アリス:: = "-"アリス Arith :: = Arith "+" Arith アリス:: = "("アリス ")"
構文を簡潔にするために、縦棒(「または」を意味する)がよく使用されます。
アリス:: =整数| 「-」アリス| アリス "+"アリス| 「( "アリス")」
TNLでは、定義された言語(この場合はArith)の名前を、Arith要素を通過するために使用される変数に置き換える、BPFの特殊なバリアントを使用します。 ここで、変数iを整数のプレースホルダーとして使用し、eをArith要素のプレースホルダーとして使用するとします。 その後、次のように文法を書くことができます。
e :: = i ∣ −e ∣ e + e
括弧を省略していることに注意してください。 一般に、どの言語でも括弧が許可されていると理解されています。 出力の概念は、解析ツリーと同じです。 どちらも、特定の要素が多数に含まれている理由を示しています。
操作上のセマンティクス
言語を記述するとは、その言語でプログラムを起動したときに何が起こるかを記述することです。 これはまさに操作上のセマンティクスが行うことです。 Arithの場合、プログラムごとに整数の結果を指定する必要があります。 前述のように、リレーションシップを使用して入力を結果にマッピングできます。 通常、これはTNPで行います。 いくつかの異なる関係スタイルがあります。 最初に検討するのは、プログラムをその結果に直接マップする大きなステップのセマンティクスです。
ビッグステップのセマンティクス
Arith要素を整数にマッピングするEvalリレーションを定義します。 たとえば、条件(-(2 + -5)、3)∈Evalを満たさなければなりません。 この関係は無限になります(Arithには無限の数のプログラムがあるため)。 繰り返しますが、一連のルールを使用してEvalを決定します。 しかし、始める前に、略語を紹介します。
 は(e、i)∈Evalを意味します。 以下に、水平表記を使用してEvalを定義するルールを説明します。 1つのプログラムを見逃さないように、各Arith構文ルールに対して1つのルールを作成します(3つあります)。 1つのルールが言語の各構文ルールに対応する場合、ルールは構文指向であると言います。
は(e、i)∈Evalを意味します。 以下に、水平表記を使用してEvalを定義するルールを説明します。 1つのプログラムを見逃さないように、各Arith構文ルールに対して1つのルールを作成します(3つあります)。 1つのルールが言語の各構文ルールに対応する場合、ルールは構文指向であると言います。
「-」で「-」、「+」で「+」を定義したのは少し奇妙に思えるかもしれません。 これは循環依存ですか? 答えはノーです。 プラスとマイナスは、誰もが学校で経験する整数の通常の算術演算です。 この意味で、Arithが32ビットまたは64ビットの算術演算を使用しないのはさらに奇妙です。 Arithを実装するプログラマは、パッケージを使用してBigIntegerを操作し、算術を処理できます。
小さなステップのセマンティクス
操作セマンティクスの2番目の最も一般的なスタイルは、小さなステップのセマンティクスです。 このスタイルでは、態度は結果にプログラムを表示しません。 代わりに、プログラムを若干単純化されたプログラムにマップします。このプログラムでは、部分式が結果に置き換えられます。 このスタイルはテキストの置換と考えることができます。 このスタイルの例を挙げるには、Stepリレーションを定義します。 この関係には、他の多くの要素と同様に、次の要素が含まれます。
(-(2 + -5)、-(-3))∈ステップ
(-(-3)、3)∈ステップ
略語を再度紹介します。
 は(e1、e2)∈ステップを意味します。 そして、ステップをまとめると、
は(e1、e2)∈ステップを意味します。 そして、ステップをまとめると、  意味する
意味する  そして
そして  。 stepの同義語は、reduceという用語です。 前の2ステップの例は、次のように記述できます。
。 stepの同義語は、reduceという用語です。 前の2ステップの例は、次のように記述できます。
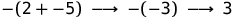
次に、Stepを定義するルールに進みましょう。 以下で説明する5つのルールがあります。
\ frac {e \ longrightarrow e '} {\ mathtt {-} e \ longrightarrow \ mathtt {-} e'} \ qquad(4)\ frac {e_1 \ longrightarrow e '_1} {e_1 \ mathtt {+} e_2 \ longrightarrow e'_1 \ mathtt {+} e_2} \ qquad(5)\ frac {e_2 \ longrightarrow e'_2} {i \ mathtt {+} e_2 \ longrightarrow i \ mathtt {+} e'_2} \ end {gather *}](https://habrastorage.org/getpro/habr/post_images/a72/c78/416/a72c784165e744663f825b7c38e0e676.png)
ルール(1)と(2)は最も興味深いものです。 彼らは算術を行います。 それらを「計算上の削減ルール」と呼びます。 ルール(3〜5)を使用すると、部分式に移動して計算を実行できます。 それらは、私たちが今に入ってこない理由でしばしば合同規則と呼ばれます。 ルール(5)で変数iを使用すると、縮小が左から右に行われることを意味します。 特に、左の式が整数になるまで、右の式を+記号から減らすことはできません。
余談:ここで検討している左から右の順序は、言語デザイナーとして選択されています。 順序を決定できず、あいまいになりました。 私たちの言語には副作用がないので、順序は関係ありません。 ただし、ほとんどの言語には副作用があり、順序を決定します(すべてではありません)。そのため、順序が通常決定される方法の例を検討する必要があると考えました。
例の時間。 ステップの出力を見てみましょう。
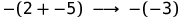
計算の1ステップ、つまり 関係ステップ。 しかし、まだ完了していません。 完了前にプログラムを実行することの意味をまだ決定する必要があります。 これを行うには、ステップ関係の観点からEvalを定義します。 言い換えれば、式eがゼロ以上のステップで整数iに還元される場合、Eval '関係には任意のペア(e、i)が含まれます。 以下に説明する新しい表記法があります。
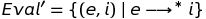
表記{... ∣ ...}はセットコンストラクタを定義します。 垂直バーの左側の式は、セットの典型的な要素のテンプレートを定義し、右側の式は、セットの要素の制限を定義します。 表記法
 ゼロ以上のステップを意味します。 ルールを使用して、これらのマルチステップリレーションシップを定義します。
ゼロ以上のステップを意味します。 ルールを使用して、これらのマルチステップリレーションシップを定義します。
(私はLispのようなリストの観点からそれについて考える。だから、最初のルールはnilであり、2番目のルールはconsである。)
型システム(例としてラムダ計算を使用)
多くのプログラミング言語は静的に型付けされています。 コンパイラーは、実際のコンパイルを実行する前にいくつかの検証チェックを実行します。 通常、チェック中に、コンパイラーはオブジェクトが適切に使用されていることを確認します。 例えば、誰も整数を関数として使用しようとしていないということです。 言語設計者がどの特定のチェックを実行する必要があるかを示す方法は、言語の型システムを定義することです。 Arithは非常に単純なので、興味深い型チェックはありません。 TNLで繰り返し使用されるより複雑な言語-ラムダ計算(技術的には、単純化されたタイプのラムダ計算)を検討してください。 ラムダ計算は、匿名関数のみで構成されます。 ラムダ計算を拡張して、算術式が含まれるようにします。 その後、私たちの言語は次の文法によって決定されます。
e :: = i ∣ −e ∣ e + e ∣ x ∣ ee ∣λx:Te
変数xは、fooやgなどのパラメーター名をリストします。 右側の次の2つの式(ee)は、関数の適用(または関数呼び出し)を意味します。 Cに精通している場合、e1 e2をe1(e2)と読むことができます。 ラムダ計算では、関数はパラメーターを1つだけ取るため、関数を呼び出すには1つの引数しか必要ありません。 構文λx:Teは、タイプTの1つのパラメーターx(すぐにタイプを決定します)と式eで構成される本体を持つ関数を作成します。 (多くの場合、xは関数の名前であると誤解されます。実際には、関数は匿名であるため、つまり名前がないため、これはパラメーターの名前です。)関数の戻り値は式eの結果になります。 次に、プログラムの実行中にどのオブジェクトが存在するかを考えてみましょう。 これらは整数と関数です。 Tを使用してさまざまなタイプを列挙し、さまざまなオブジェクトを記述するために多くのタイプを作成します。

機能タイプ
 、T 1はパラメーターのタイプ、T 2は戻り値のタイプです。
、T 1はパラメーターのタイプ、T 2は戻り値のタイプです。
型システムの仕事は、式の結果が持つ値の型を予測することです。 たとえば、式-(5 + 2)はInt型である必要があります。これは、結果-(5 + 2)が数値-3(整数)であるためです。 言語の構文または操作上のセマンティクスを決定する場合と同様に、TNC理論家は関係と規則を使用して型システムを決定します。 WellTypedリレーションを定義します。これは、最初の近似では、式を型にマッピングします。 たとえば、(-(5 + 2)、Int)∈WellTyped。
ただし、 ラムダ計算には変数が含まれます。どの変数がどのタイプを持つかを追跡するには、何らかの種類のシンボルテーブルアナログ、タイプ環境と呼ばれる関係が必要です。 ギリシャ文字のΓ(ガンマ)は、この目的で一般的に使用されます。 外部スコープから変数を隠す機能を備えた、古いものから新しいタイプの環境を作成できる必要があります。 これらの可能性の数学的装置を決定するために、xで始まるタプルが除外されることを除き、Γ∖xはΓと同じ関係になると仮定します。 (型システムの定義方法によっては、xで始まる0または1タプルがあり、型の環境を部分関数と呼ばれる特別な種類の関係にする場合があります。)型環境を変数xで拡張し、場合によっては以前の定義をオーバーライドし、次のように定義します。
と仮定する
それから
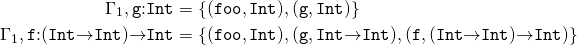
型環境は、コンパイラーのグローバルシンボルテーブルとは異なり、スコープごとに複数の型環境がある場合があります。 さらに、タイプ環境を更新せず、代わりに、古い環境とわずかに異なる新しい環境を作成します。 プログラミングの観点から、ここで使用する数学的メタ言語は純粋に機能的です。 副作用は含まれていません。 読者はこれが非効率につながるのではないかと心配するかもしれませんが、ここでプログラムを書いているのではなく、仕様を書いていることを思い出してください! 明快さは私たちにとって最も重要です。 そして、清潔に保つことで、より理解しやすいものを書くことができます。
WellTypedリレーションに戻ると、2つの要素のタプル(2タプル、ペア)を含む代わりに、3つの要素のタプル(3タプル、トリプル)の形式(Γ、e、T)が含まれます。 したがって、型環境のコンテキストで型を式に割り当てます。 もう1つの略語を紹介します(TNL理論家は略語が大好きです!)。 書きます
 (Γ、e、T)∈WellTypedの代わりに。 これで、WellTypedを定義するルールをリストする準備ができました。
(Γ、e、T)∈WellTypedの代わりに。 これで、WellTypedを定義するルールをリストする準備ができました。
![\ begin {gather *} \ frac {} {\ Gamma \ vdash i:\ mathtt {Int}} \ qquad \ frac {\ Gamma \ vdash e:\ mathtt {Int}} {\ Gamma \ vdash \ mathtt {-} e:\ mathtt {Int}} \ qquad \ frac {\ Gamma \ vdash e_1:\ mathtt {Int} \ quad \ Gamma \ vdash e_2:\ mathtt {Int}} {\ Gamma \ vdash e_1 \ mathtt {+} e_2 :\ mathtt {Int}} \\ [3ex] \ frac {(x、T)\ in \ Gamma} {\ Gamma \ vdash x:T} \ qquad \ frac {\ Gamma、x {:} T_1 \ vdash e :T_2} {\ Gamma \ vdash(\ lambda x {:} T_1。E):(T_1 \ to T_2)} \ qquad \ frac {\ Gamma \ vdash e_1:T \ to T '\ quad \ Gamma \ vdash e_2 :T} {\ Gamma \ vdash e_1 \、e_2:T '} \ end {gather *}](https://habrastorage.org/getpro/habr/post_images/491/925/cc3/491925cc3120afcc0dcce1e0829ca1d3.png)
上記のルールを要約します。 算術演算子は整数で機能します。 変数は環境からタイプを取得します。 ラムダは、パラメーターのタイプと結果の出力タイプに基づいた機能タイプです。 ラムダ本体は、このラムダのパラメーターを使用して展開され、作成ポイントからの環境を使用してチェックされます(字句スコープ)。 また、関数の使用は、引数の型がパラメーターの型と一致する限り、言語のロジックに違反しません。
おわりに
これで、プログラミング言語の理論で使用されている表記法でこのクラッシュコースが終了します。 この投稿では基本のみを説明していますが、必要な追加の表記法の多くは、ここで説明した表記法のバリエーションです。 お読みいただき、コメントで質問してください。