内容

1. テンソルとは何ですか、なぜ必要ですか？
2. ベクトル演算とテンソル演算。 テンソルランク
3. 曲線座標
4. テンソル博覧会のポイントのダイナミクス
5. テンソルのアクションとその他の理論的な質問
6. 自由固体の運動学。 角速度の性質
7. ソリッドの最終回転。 回転テンソルのプロパティとその計算方法
8. Levi-Civitaテンソルの畳み込みについて
9. 最終回転のパラメーターによる角速度テンソルの導出。 頭とマキシマを適用
10. 角速度ベクトルを取得します。 欠点に取り組む
11. 自由な動きでの体のポイントの加速。 ソリッドの角加速度
12. 固体運動学におけるロドリゲハミルトンパラメーター
13. テンソル式の変換の問題におけるSKA Maxima。 ロドリゲ・ハミルトンのパラメーターにおける角速度と加速度
14. 剛体のダイナミクスの非標準的な紹介
15. 非自由な固体運動
16. 固体の慣性テンソルの特性
17. ナットジャニベコバのスケッチ
18. ヤニベコフ効果の数学的モデリング

はじめに

前回、ダランベール原理に基づいて剛体の運動の微分方程式を取得する方法の1つを検討しました。 運動方程式の一般的な形に決めました









しかし、これらの方程式を注意深く見て、私は批判されるべきです-事実は、これらの方程式では未知数の数が多すぎるということです。 不明な点には、極の加速度が含まれます。 体の角加速度 結合反応と同様に 。 体の動きが少なくとも1つの接続によって制限されている場合、（1）および（2）の未知の量の数は方程式の数を超えます。



これは、方程式（1）および（2）の左辺に、身体の自由な動きの場合に計算された加速度が含まれている、つまり、過剰な座標があるためです。 したがって、システム（1）、（2）は、身体上の点の座標、速度、および加速度に対する制約によって課せられる制約を記述する制約方程式によって補足される必要があります。



これが今やろうとしていることです-制約の方程式を追加したときに方程式（1）と（2）がどのようになるか、そして得られた方程式が実際的な意味で私たちに与えるものを見てください

1.自由固体の運動方程式

フリーボディは、その動きが結合によって制限されないボディと呼ばれます。 したがって、方程式（1）および（2）では、余分な未知数が消えて、









また、自由体の場合、任意の極を使用することは意味がありません-慣性系の減少の中心を体の重心に変更して、運動方程式をより簡単な形式で書き留める方がよい









方程式（5）および（6）は、剛体の自由運動の微分方程式です。 それらは、加速度に関して解決され、与えられた初期条件下で数値的に統合されます。

2. 1つの固定点を持つ剛体の運動方程式

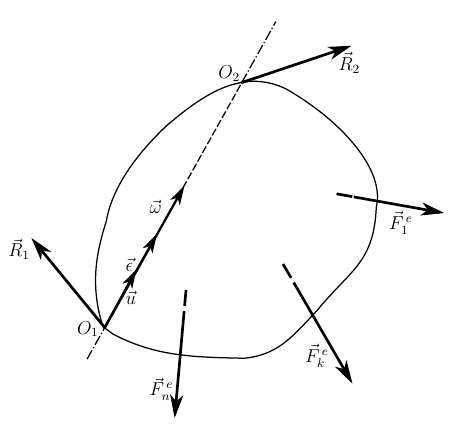
ここで、身体の動きが、次の場所にある球面ヒンジによって制限されているとします。 。 次に、この固定点で極を選択することにより、制約方程式を追加できます













1つの力で表される球面関節の反作用 したがって、（7）を考慮して、式（1）および（2）は次の形式で書き直すことができます。









さらに 強さから ポイントで適用 、ついに









方程式（8）では、問題の初期条件と身体に加えられる既知のアクティブな力に基づいて身体の角加速度を決定できます。方程式（9）では、角加速度を知ることで、球形ヒンジの反作用を見つけることができます。 したがって、球運動の微分方程式を取得します。

3.体の回転運動。 軸を中心とした物体の慣性モーメント

回転とは、ある時点で2つのポイントが動かないままになっているときの身体の動きです。 方程式を使用してこの事実を表現すると、次の関係方程式を書くことができます。













条件（10）は体の点の1つの不動性を表し、条件（11）は体の回転軸の方向の不変性を表します。 （11）に基づいて、最終回転のパラメーターを使用して、体の角速度と角加速度を書き出すことができます。









式（2）に（12）と（10）を代入します









2つの結合があり、それに応じて、ボディが回転するベアリングからの2つの反応があると仮定します。 そして、あなたはすぐにそれを考慮することができます 最初の反応がその時点で適用されるため 。 さらに、回転軸の単位ベクトルによる最後の方程式のスカラー乗算を実行します









二次反応の瞬間は次のように計算できることを考慮します。 ながら 、つまり、









この方程式の両側の2番目の項は、共面ベクトルの混合積であり、ゼロに等しいため、結果として、









-固定軸の周りの身体の回転の微分方程式、ここで









回転軸に対する固体の慣性モーメントと呼ばれ、









-この点を通過する軸上の固定点に対するベクトルモーメントの投影、または- 軸に対する力のモーメント 。



式（14）は非常に興味深いものです。 テンソル形式で書き換えると、式が得られます









固体のよく知られた慣性テンソルに従って、対象の回転軸に対する慣性モーメントを決定できます。空間の方向は、単位ベクトルによって与えられます 。 慣性モーメント（16）は、回転軸の周りの体重の分布を特徴付けるスカラー量です。 この量と式（13）は、理論力学の一般的なコースからよく知られています。

4.体の進行性の動き

並進運動中、身体に加えられた結合は、その回転を妨げます。 この場合、明らかな平等を書き留めることができます









債券が理想的であると仮定すると、彼らの反応に課せられた条件を書き留めることができます









どこで 体の点の軌跡に接するベクトルです。 並進運動の場合、そのすべての点の軌道は同じであるため、軌道への接線のベクトルはすべての点で同じです。 （17）と（18）を考慮して、式（1）を書き換えることができます。









または









-その点の軌跡への接線への投影における物体の並進運動の微分方程式。

おわりに

この記事では、剛体（1）および（2）の一般的な運動方程式を、拘束方程式で補足した場合にどのように変換されるかを調べました。 同時に、理論力学によって研究された身体運動のすべての特別な場合について、運動の微分方程式を簡単かつ自然に構築しました。

謝辞

この記事を準備する際に、 SeptiMユーザーによって提案された方法は使用されました 。 仕事の明らかな利便性に関連して、著者に感謝します。



継続するには...