
クリストファー・カールソンの「 ツイスト・アーキテクチャー 」投稿の翻訳。
翻訳に協力してくれたKirill Guzenko KirillGuzenkoに感謝します。
ノーマンフォスターのハーストタワーをメビウスのテープにねじ込んで宇宙に送ったり、 メアリー・エックスと一緒にタンゴを踊らせたりするタスクを自分で設定したわけではありませんでした。 これはMathematicaを使用する専門的なリスクの1つです。
それはすべて、ロフトにおける無実の実験から始まりました-造船から来たスキニングとしても知られている技術です。 私の研究の目的はいくつかの3次元形式であり、ロフトは迅速に結果を得るための素晴らしい方法のように思えました。 3次元の等高線の順序付けられたセットを取り、それを多角形に適合させるロフト関数を作成しました。
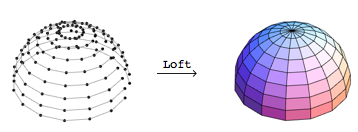
トポロジからポリゴンのジオメトリを分解するために、 ロフトはMathematicaの GraphicsComplexプリミティブを使用します。 輪郭点の座標は、最初の引数で収集されます。 2番目の引数はポリゴンのリストであり、その座標値は座標リスト内の整数インデックスに置き換えられます。 ロフト関数を記述することは難しくありませんでしたが、目的のポイントに関連付けられたポリゴンにインデックスを付けるには少し想像力が必要でした。

マニピュレート機能を介してロフトと協力し、私の研究でいくつかの新しい興味深い形式を発見できたことを非常に喜んでいます。 デモをダウンロードして、自分で試すことができます。

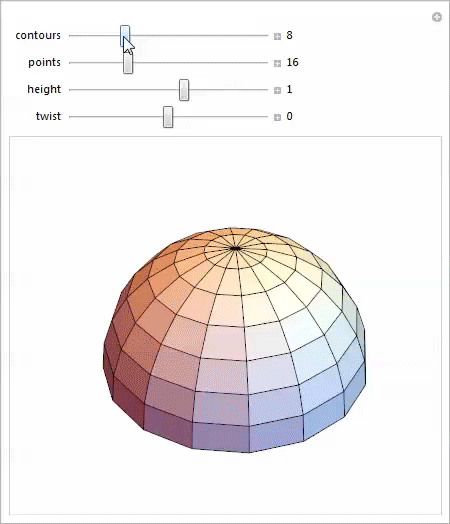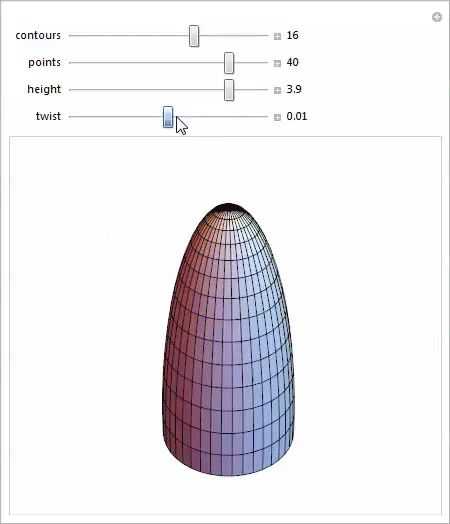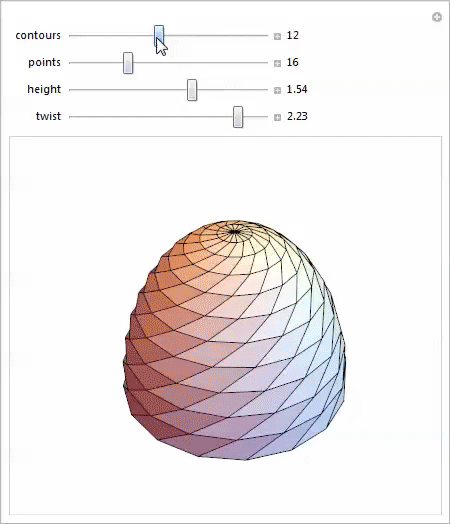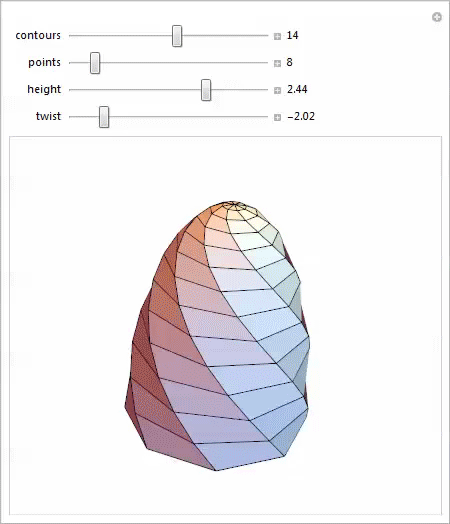
スケーラブルなツイスト半球のこの些細なパラメータ化でさえ、驚くべき多様な形状を与え、それぞれが興味深い研究の可能性を提供します。
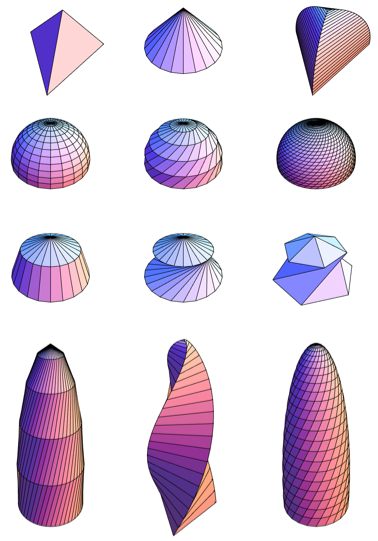
これらの最後のフォームは、地元の人々がキュウリ(以下、Mary-Exと呼ぶ)と呼ぶロンドンのノーマン・フォスター・スイス・リーの建物を考えるきっかけになりました。

Mathematicaで Mary-Exモデルがどれほど妥当であるかに驚いた。 私の単純なロフト関数は、Mary-Ex対角線グリッドの作成に対応できないことがすぐに明らかになったため、最初にこの関数を一般化することにしました。
ステップバイステップで、Mary-Exだけでなく、パネルとそのフレームの組み合わせに基づいた他の多くの建築形態をシミュレートする機会がありました。
私のBuild関数はLoftのように機能しますが、チューブやポリゴンなどの要素、および等高線グリッド上に配置するためのアルゴリズムをより柔軟に指定できます。 Loftと同様に、 Buildの最初の引数はパスのセットです。 2番目の引数は、等高線グリッド上の配置のアルゴリズムを定義する追加の引数を含むGraphics3Dプリミティブのリストです。
下から上に番号が付けられた輪郭と左から右に輪郭の点を想像すると、インデックス{point、contour}は整数座標系の座標に対応します。
これは、 ポリゴンプリミティブ[{{0,0}、{1,2}、{1,0}}]がグリッドに配置される方法です。
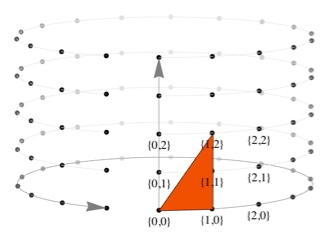
追加の繰り返し引数を含まないプリミティブは、グリッド上に自動的にコピーされます。 要素のコピーの配置のタイプを明示的に指定する方法は、Polygon [{{0,0,0、{1,2}、{1,0}}、{{2,0}、{1,1}}のように、転送ベクトルのペアを定義することによって行われます]。 このポリゴンがグリッドにどのように収まるかを以下に示します。
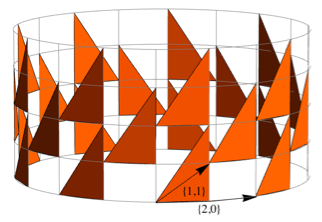
LineやTubeなどの線形プリミティブでは、繰り返し引数はプリミティブが水平方向にブロードキャストされる頻度を指定し、水平プリミティブの場合は垂直方向にブロードキャストされます。 Buildは、ポリゴン、チューブ、ラインの繰り返しを組み合わせることで、パネルとフィーチャのアセンブリを定義する際の柔軟性を高めます。 ここに、 Buildプリミティブの使用を示すために作成した抽象的な構造を示します。


Buildができたので、次のタスクはMary-Exプロファイルの形状を決定し、対応する等高線グリッドを構築することです。 いつものように、最初に簡単な方法を見つけようとして、まず扁平な楕円体を試しました。その結果、メアリーアックスの頂点が楕円体に対して鋭すぎることがわかりました。 他の単純な数学的形式は思いつかなかったので、スプラインを通して任意の形状の輪郭を設定することにしました。
任意の形状の回転体をシミュレートするために、同僚のユ・ソンチャンによって書かれたこのPotter's Wheel Demonstrationデモを思い出しました。 それがまさに必要なものでした。
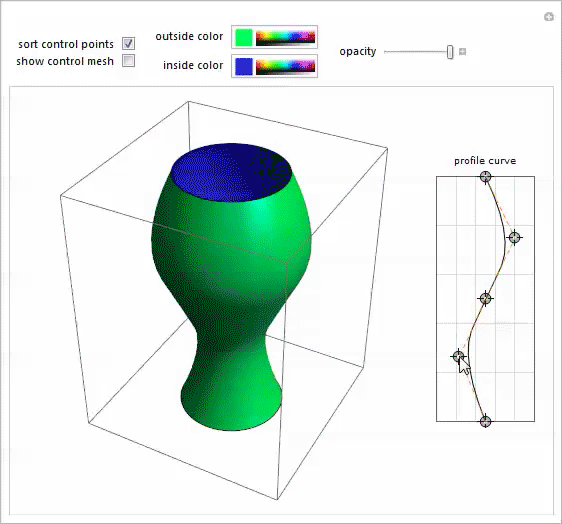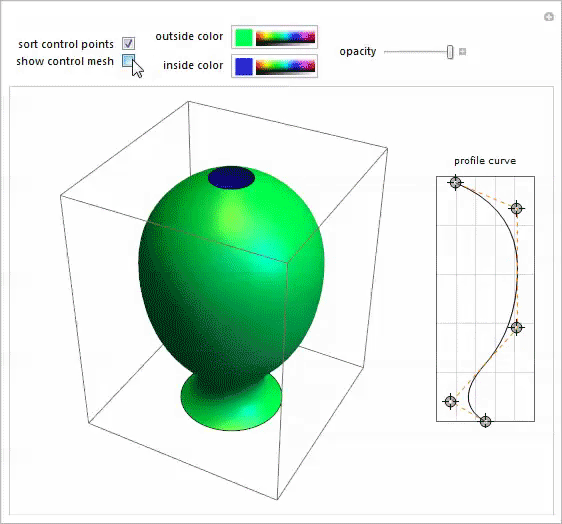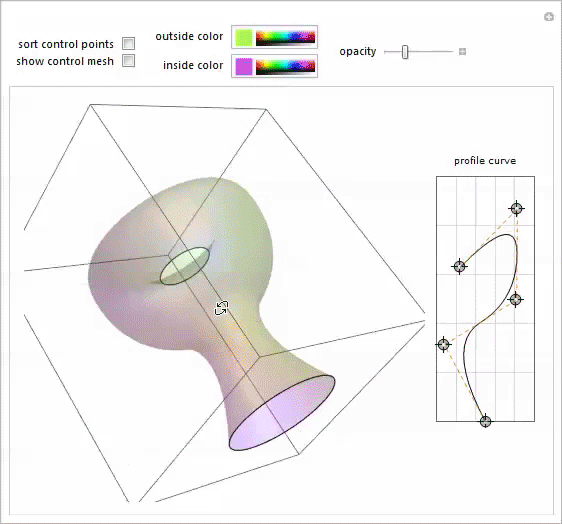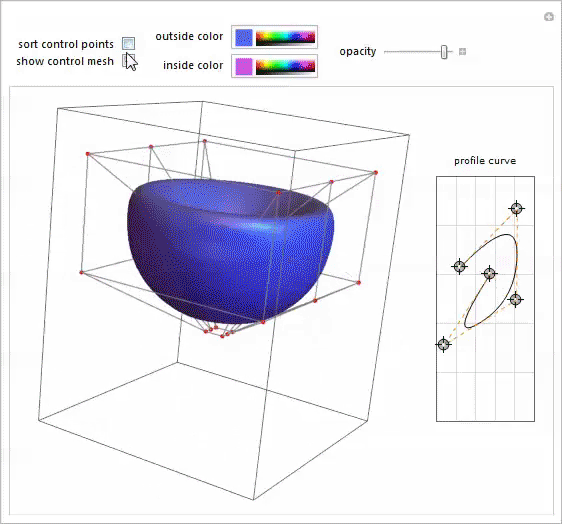
Mary-Exの写真を別のノートブックで開き、スプラインプロファイルのポイントを移動して、その形状の許容可能な近似値を取得しました。
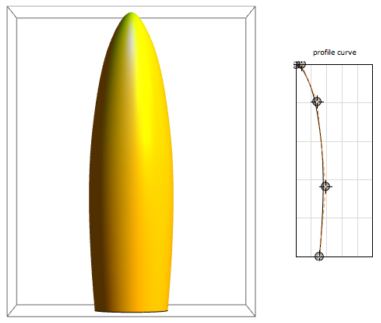
結果に満足したら、 Maniulateの 「Paste Snapshot」を使用して、この形状のソースコードを取得しました。 ソースコードから、スプラインコントロールポイントの座標を取得し 、プロファイルを設定するBSplineFunctionに挿入しました。

最後のステップは、曲線プロファイルを等間隔の水平セクションに分割することでした。 Mathematicaの多目的なメッシュ作成機能により、これを行うことができます。


プロット結果からグリッドポイントの座標を抽出し、プロファイル境界ポイントを追加し、座標をyでソートして、Mary-Ex等高線グリッドを作成できるポイントのリストを取得しました。

輪郭自体は回転体に対応し、さらに、プロファイルポイントの半径方向の座標はx 、高さ座標はy 、輪郭の周りのポイントの数はMary-Exガラスパネルの数の2倍です。

Buildをテストして、輪郭点の正しい表示を確認しました。 必要なものが判明しました。
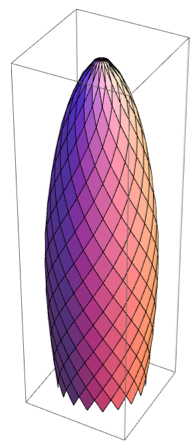
最後の手順として、Mary Axの上部にある境界リングの輪郭点の座標を見つけて追加しました。
Buildを使用して既製のモデルを作成するのに非常に多くの骨の折れる作業が必要であることは否定しません。 Mary Exの建物、屋根、上部ドーム、リング、境界、および個々のパーツ間の移行-すべてに個別のアプローチが必要でした。 マテリアルとライティングのプロパティを選択するには、目的の値が得られるまでスライダーを操作してねじります。 そして、これが結果です。

完成したモデルを入手した後、調査を開始できました。 Mathematicaのユニークな長所の1つは、置換ルールを使用して構造を後処理できることです。 Mary-Exの最終モデルは、建物の暗いパネルと明るいパネルに設定した色で表示されました。 これらの色を新しい色に置き換えて、イギリス国旗に基づいてこのカラーバリエーションを作成しました。



置換ルールを使用した後処理は、オブジェクトの外観属性だけでなく、そのジオメトリにも適用できます。 そして、私のモデルのすべての座標がGraphicsComplexの最初の引数にあるという事実は、座標変換を特に簡単にします。 また、すべてのグラフィックプリミティブは同じ座標にアタッチされているため、変換中にプリミティブは座標とともに自動的に移動します。
この手法を使用して、Mary-Exの放射状ジオメトリのバリエーションを調べるためにこのManipulateを作成しました。


今、私はいくつかの興味深い質問に対する答えを得る機会があります。 しかし、Mary-Exが丸ではなく両面だったらどうなるでしょうか? 三方? 四つ?

メアリーアックスの暗い部分が建物に沈んだらどうなるでしょうか? しかし、窪地が彼らに反対した場合はどうでしょうか? しかし、ロンドンが本当に強力な地震にショックを受けた場合はどうでしょうか?

これらすべての質問に対する答えは、 Mathematicaの Manipulateを使用して簡単に取得できます。 シュルレアリスム-スライダーが「現実」に対応する位置から移動する距離として単に定義されます。 私の研究は、この周りのどこかで(ダリスタイルで)Mary-Exが自分自身と踊るところで終わりました。

Mary-Exとの仕事の結果に触発され、私は別の斜めのメッシュフォスタービル-ニューヨークのハーストタワーに注目しました。

Mary Exと比較すると、Hearst Towerのシミュレーションはささいなものでした。 唯一の困難な瞬間は、交互に突出したポリゴンとdrれたポリゴンでコーナー領域を作成することでした。 残りは、 ビルド機能を簡単に使用するためのものでした。 これがMathematicaのデフォルトの照明で視覚化されたタワーの基本構造の私のモデルです。

塔の構造は、ポリゴンの定期的なブロードキャストによって作成されます。 楽しみのために、放送を回転に置き換え、いくつかのフロアを追加した後、この湾曲したタワーを作成し、トーラスに変えました。

さらに進むことに決めて、数秒をかけて、最初の軸に垂直な軸の周りに2番目の回転を追加し、そのような「メビウス」の建物を作成しました。 斜めのグリッドと曲がりくねったメビウスの表面の組み合わせによって生成されるこの美しいリズムが好きです。

おそらく地球上では、メビウスの建物を売るのは難しいでしょう。 しかし、私はそれが宇宙に浮かぶことを想像します-美術の宇宙ギャラリー-訪問者が次のようなことを言うようなひねりを加えた一種のグッゲンハイム軌道ギャラリー:
2001:A Space Odysseyのベルクロスリッパとソフトヘルメットを着用し、右側の壁に掛かっている作品に注意してください。 ギャラリーの周りを一周したら、天井にぶら下がって、反対側の壁を見ます。もちろん、それは同じ壁です-ギャラリーにあるのはそれだけだからです。 天の川の景色、そしておそらくどこか遠くを飛んでいる地球をお楽しみください。

