
きっとあなたも疑問に思いました:地獄はここに何と書かれていますか? この引用からの式は、高等数学教育を受けた人にとって、この質問が好奇心seventh盛な7年生と同じくらいに生じるという点で興味深い。 好奇心Non盛な7年生は、この記事の範囲を超えるわずかに異なる範囲の興味を持っています。 しかし、彼らでさえ「これらのクレイジーなオタク」を笑い回る喜びを否定することはありません。
次のテキストでは、この神秘的なキャラクターの組み合わせの秘密を明らかにします。 カットの下に来てください、しかし、バザールでバナッハ=タルスキーのパラドックスについて話された好奇心Bar盛なバーバリアン、彼女が心を失った理由、彼女の鼻を有限個のパーツに切り分け、そこからアレクサンダーの角のある球を接着した興味深い物語を覚えています。
これらの人々は誰ですか?
履歴情報に興味がない場合は、 次のセクションに進んでください。
それで、ポアンカレを引用し、順番に特定のブラリ・フォルティを引用している匿名著者のテキストからの引用です。 このすべてのポストモダニズムを理解するために、トップレベルの引用の著者から始めましょう。 彼の名前はヴィクトル・フィリッポヴィッチ・シュラヴレフであり、物理科学と数理科学の博士、教授、ロシア科学アカデミーの学者であり、「理論力学の基礎」というタイトルで本の著者でもあります。 上記の式が発生するのは、ページ番号8(2008年版を見た場合)の中でです。 ここでは、その目的を明確にするために少し説明します。
力学の過程での古典力学の形式的公理化の提示は不適切であることに注意してください。これは実際には数学的論理の頭であり、適切な力学ではないからです。
同様に、算術の公理化は算術自体の対象ではありません。 <同じ引用が続きます。再入力しません>
そのため、力学では、読者が十分な物理的直観を持っていると仮定して、基礎の説明が過度の形式主義で過負荷にならないようにすることは理にかなっています。
ポアンカレとは誰なのか、説明する必要はないと思います。 最近の出来事に照らして、テリーの人道主義者でさえ、この姓を「仮説」という単語と別の姓「Perelman」と組み合わせて覚えておく必要があります。 非常に簡単な場合(19世紀半ばから現在まで、石の袋に座っていた人たちにとって)、ジュールアンリポアンカレは史上最高の数学者の1人であり、百科事典の科学者、トポロジーの作成者、相対性理論の数学的基礎、あらゆる種類の面白い有用なものです。 引用された引用は、1910年版のScience and Methodから引用したものです。 この作品は、さまざまな数学的、科学的、哲学的および教訓的なトピックに関するエッセイのコレクションです。 非常に好奇心が強く、読みやすく、まだ関連性のあるもので、引用よりも完全に少ないものです。
ここに、例えば:
多くの心が数学を理解することを拒否していることをどのように説明するのですか? これは逆説的ですか? 実際、ここにあるのは、論理の基本原則にのみ訴える科学、例えば矛盾の原則に訴える、いわば私たちの理解の骨格を構成するものに訴える科学であり、それ自体を同時に拒否することなく放棄することのできないものに訴えるそれでも、この科学を暗いと感じる人がいます! そして、これらの人々のほとんど! 彼らが発明できないようにしましょう-これはまだ許されています。 しかし、彼らは提供されている証拠を理解していません。彼らは、きれいで明るい炎で燃える光を彼らにもたらすとき、彼らは盲目のままです-それは非常に奇妙です。
または一方で:
ここで4年生。 教師は、「円は、中心と呼ばれる1つの内部点から同じ距離にある平面上の点の幾何学的位置です」と指示します。 良い生徒はこのフレーズをノートに書きます。 貧しい学生は彼女に「小さな男」を描きますが、誰も何も理解しませんでした。 その後、教師はチョークを取り、黒板に円を描きます。 「ええ、学生たちは、「なぜ彼はすぐに言わなかったのですか。円は円であり、すぐに理解できるでしょう」と考えています。」
ただし、特定の引用に興味があります。 次のように始まる「数学と論理」の章にあります。
最初に数学に特有の原則に頼らずに数学を論理に還元することは可能ですか? 数学者の学校があり、大義に対するすべての情熱と信仰をもって、これを証明しようとしています。 彼女は特別な言語を開発しました。この言語では、言葉はなく、標識のみがあります。 この言語は少数のイニシエーターによってのみ理解されるため、冒とく者は熱心な信奉者のカテゴリー的な声明に屈する傾向があります。
読者は、さらに議論されることをすでに理解していると思います。 いくつかの激しさを伴うポアンカレは、理解できない表記法と基本の修正によって「新しい学校」の数学者を攻撃します。 その後の出来事が示したように、この問題で彼は逆行者であることが判明しました-しかし、彼にはこの理由がありました。 厳しい1890年代に数学で起こったことは、この熱狂的なフランス人よりも無関心な人を驚かせた。
それで、チェーンの終わり、内部引用符を含まない引用符に到達しました。 著者はチェサレ・ブラリ・フォルティです。数学者はそれほど偉大ではありませんが、いくつかのパラドックスのおかげで歴史に名前を書くことができました。 彼に関する情報はかなり不足しており、彼の姓のストレスがどれほどあるかを見つけることさえできませんでした。 この記事を書くように勧めた公式は、彼の記事「The Transfinite Numbersの質問」に含まれていました。 この記事は、有名なトロツキストのジャン・ファン・ハイエノルトの著書「From Frege ToGödel:A Math Book in Mathematical Logic」(以下、5月の英語はノートとノートからのものであるため、名前を翻訳するリスクはありません)で本を見つけました。 Peanoの記事「算術の原理、新しい方法によって提示された」が彼女の本に含まれていたので、これは大成功でした。 この記事では、「少数のイニシエーターのみが理解できる指定」が紹介されましたが、それなしでは、ブラリ・フォルテの記事は中国語と同じでした。
ちなみに
同じPeanoの記事の内容の簡単な改作が私のハブの1つにあります
叙情的な余談
面白いクラッカーを見たくない場合は、 次のセクションに直接進んでください。
van Heyenortの本のPeanoとBurali-Fortiの記事の前に、Fregeの記事「概念の計算、または算術を模倣した純粋な思考の形式言語」がありました。 数学者で哲学者であるフリードリッヒ・ルートヴィッヒ・ゴットロブ・フレーゲは、原則として、述語計算の作成者と見なすことができます。 彼はこのhabrapostのトピックとはかなり間接的な関係にあります(ポアンカレは本の中でそれを言及していませんでしたが、実際、数学を論理に還元することでこの混乱をすべて醸造したのはフレーゲでした)。 しかし、私はその最もファッショナブルな指定を共有するのを助けることができませんでした。 幸いなことに(または不幸なことに)、彼らはその複雑さのために現代の数学的論理に根を下ろしませんでした。 もちろん、フレーゲは「印刷会社のタイプセッターの利便性は間違いなく最高の利益ではない」と述べましたが、見てわかるように、この要因も一定の役割を果たしました。 しかし、かなり序文。
見よ! 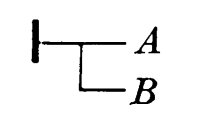
「AからBに続く」

「AからBに続き、これからGに続く」
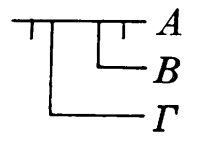
「Aの否定からBに続き、Gに続くことは真実ではない」

「地獄のhを民族の恐怖で分けた」

「Ph'nglui Mglv'nafh Cthulhu R'laih vgah'nagl fhtagn!」 アギアクトゥルフ、アギアダゴン!」
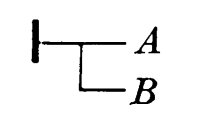
「AからBに続く」

「AからBに続き、これからGに続く」
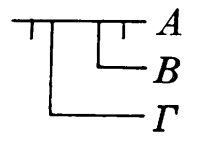
「Aの否定からBに続き、Gに続くことは真実ではない」

「地獄のhを民族の恐怖で分けた」

「Ph'nglui Mglv'nafh Cthulhu R'laih vgah'nagl fhtagn!」 アギアクトゥルフ、アギアダゴン!」
もちろん、「これですべて」とはほど遠い人にとって、述語論理式の現代の表記法はもう少し明確に見えることを認めなければなりません。
理論情報
序数が何であり、ブラリフォルティパラドックスが何であるかを知っている場合は、すぐに最終セクションに進むことができます。
ドイツの数学者ゲオルク・カントールは、無限の多様性を理解し始めた最初の一人です。 彼の前には、これらの品種のうち、 潜在的な無限大と実際の無限 大の 2つしかありませんでした。 これらの概念は次のように説明できます。
- 潜在的な無限大。 リンゴの束があり、毎日別のリンゴをそこに置いたとします。 遅かれ早かれ、山の中のリンゴの数は、事前に与えられた数よりも多くなります。
- 実際の無限。 リンゴの数が無限にある束があるとします。
数学のある時点まで、潜在的な無限大にのみ遭遇し、神学者だけが実際の無限大に作用して、神のさまざまなカテゴリーを説明しました。 数学に実際の無限大を大まかに導入したカントールは、前述のポアンカレを含む宗教的人物と現代の数学者の間でbothりの波を引き起こした。 さらに、慎重に検討すると、実際の無限大は異なることが判明しました。 自然数の数は1つの無限大であり、実数の数は別であり、2番目の無限大は1番目の無限大よりも大きくなります。 そして、実引数の関数の数は3番目の無限大であり、最初の2つの組み合わせを超えています!
自然数は有限量を示すために使用されますが、無限量はどうですか? これを行うために、自然系列は多くのいわゆる基数に拡張されました。 基数は、特定のセットの要素の数(広義の意味)です。 単位-1つの要素のセット内の要素の数。 2-2つの要素のセット内の要素の数。 さらに、自然数の場合、自然数の数に等しい数N 0が織られます。 一般的に、文字Nの代わりにヘブライ語の文字「Aleph」があるはずですが、適切なUnicode文字を挿入しようとすると、
したがって、N 0には特定のN 1 が続きますが、どのセットがそれに対応するかという問題は自明ではないことが判明しました( 連続体の仮説を参照)。 「次の数」の概念では、有限から無限への移行に問題が生じました。
しかし、他の「無限数」があります-いわゆる序数 、それらは序数であり、カントールによって発明されました。 それらの定義はかなり複雑ですが、簡単に説明します。 基数が単純なセットに対応する場合、序数は順序付きセットに対応します。 示されている2つの要素のいずれかについて。 どちらが大きいか、小さいか。 順序関係はいくつかの明白な基準を満たさなければなりません。 さらに、序数を構成するために、順序付きセットに追加の条件が課され、その下で完全に順序付きと呼ばれます。 2つの完全に順序付けられたセット間で順序関係を保持する明確な対応を確立できる場合、これらのセットは同じ順序を持ちます。
有限の序数は自然数にマッピングできます。 たとえば、セット{1、2、3}の序数は自然数3に関連付けることができます。序数は一緒に加算できます。有限の序数の場合、加算は自然数の加算と一致します(たとえば、Ord {1、2} + Ord {1 、2、3} = Ord {1、2、3、4、5})。 2つの序数を追加するには、それらに対応するセットを取得し、それらを1つのセットに結合して、次の順序関係を設定する必要があります。
- 同じソースセットの2つの要素を比較する場合、そのセットにあった順序関係を使用します
- 異なるソースセットの2つの要素を比較すると、2番目のセットの要素は常に大きくなります
このような多数の序数は、序数の合計になります。 したがって、次の序数の決定に問題はありません。前の序数を取り、それに序数1を追加するだけです。
自然数のセットの序数は、文字ωで示されます。 その後に順序ω+ 1が続きます。これは、他のどの数値よりも大きい「最後の」数値を追加した自然数のセットに対応します。 次に、序数ω+ 2が来ます。これは、「最後」と「最後から2番目」の数を持つ自然な系列に対応します。 また、2ω(自然数列、その後に別の自然数列)、3ω、4ω、ω2、ωωなどの序数があります...
ご覧のとおり、Cantorは大きなジョーカーでした。 皮肉なことに、彼の理論の終わりの始まりをマークしたのは序数であり、後に「単純集合論」と呼ばれることになります。 序数を使用して、Burali-Fortiはパラドックスになりました。 彼の推論の過程は次のようなものでした:多くの序数を取り、それがかなり秩序立っていることを証明します。 だから、彼自身はいくつかの序数に対応しています。 この序数が他の序数以上であることを証明しましょう。 それに1つ追加します。 びっくりした目をしてください。
今、知識と熱意を持って、私たちは底に行き、ハブラポストの一番初め、はるか上にあるこの式が何を意味するのかを理解する準備ができています。
エッセンス
ブラーリ・フォルティの指定を理解することは容易ではありませんでした。 ペアノによって導入された記法に、彼は彼自身の記法をいくつか追加しました。 Peanoとは異なり、彼は記事の冒頭で彼の革新について詳しく説明していませんでした。 おそらくこれらの説明は他の場所に含まれていますが、残念ながら(または幸いなことに)インターネット上でブラリフォルティの完全な作品を見つけることができませんでした。 したがって、いくつかの場所で、文脈に基づいて意味を考えなければなりませんでした。 このプロセスは、 有名な NSA パズルの解を連想させます。
そもそも、ポアンカレ(そして次にズラヴレフ)の式は間違っています。 オリジナルでは、次のようになります。

2つのオーバーレイに注意してください;それらの存在は基本です。
ここでの文字「イプシロン」は帰属を意味し、それから現代の記号「ε」が始まりました。 Unは、1つの要素のみを含むすべてのセットのセットです。 したがって、「uεUn」という表記は、uが1つの要素を持つセットであることのみを意味します。 このような自明ではない表記法は、表記法u = {a、b、c ...}による個々の要素のセットの「構築」がまだ採用されていないという事実によって引き起こされているようです。
下線を引くことにより、Burali-FortiはPeanoによって「反転の兆候」として導入された角括弧を置き換えます。 ペアノは、かなり幅広いケースでそれを使用しました。 たとえば、その中のb [+ a]はbaを意味し、式[sin](x)はarcsin(x)を象徴していました。 表記[xε](特定の条件)は、この条件を満たす多くのXを意味しました。 したがって、表記[(u、v)ε](uεUn)は、「uが1つの要素のセットであるようなペア(u、v)のセット」を意味します。 Habra Editorでマークアップを追加する便利な方法が見当たらないため、おそらくPeanoの表記を使用します。
Koは、順序付きセットのセットです。 Burali-Forti順序セットは、ペア(セット、順序関係)として定義されます。 したがって、表記{Ko⋂[(u、v)ε](uεUn)}は、単に「順序付けられたシングルトンセットのセット」を意味します。
「T '」文字の組み合わせを使用して、Burali-Forteは序数を取る操作を示します。 より厳密には、式T '(u、v)は、順序vの関係が与えられているセットuの序数を意味します。 ただし、ここでいくつかの矛盾があります。検討中の式では、関数T 'はペア(セット、順序関係)ではなく、そのようなペアのセットに適用されます。 コンテキストに基づいて、そのような場合に関数が各要素に適用される特定の合意があり、出力はすべての要素の値で構成されるセットであると仮定することができます。 この読みでは、T '{Ko⋂[(u、v)ε](uεUn)}は、すべてのシングルトン順序セットの序数のセットです。 すべてのシングルトン順序セットは同等であるため、この順序のセットには要素が1つだけ含まれます。これは順序単位です。
ダッシュで波打つことに関しては、彼女の理解で、私はほとんどの問題を抱えていました。 ブラーリ・フォルティの他の作品を探す必要がありました。 それらの1つである「Logica Matematica」(明らかに教科書ですが、イタリア語で書かれているので完全にはわかりません)では、L関数が見つかりました(小文字の「l」がありましたが、杖のように見えますが、したがって、明確にするために、大文字を使用します)。 次のように機能します。引数を取り、それをセットに変換します。その唯一の要素はこの引数です。 現代の表記では:L(x)= {x}。
波線をLとして識別し、ダッシュを逆として識別した場合、[L]はセットから唯一の要素を抽出する逆変換であることがわかります。 この場合、[L] T '{Ko⋂[(u、v)ε](uεUn)}は実際には単位です。 通常のユニットですが、これらは些細なことです。
次回、誰かがこの式で写真を見せたとき(そしてこれが起こると、これはインターネットです)、この式の意味を彼に伝えることができます。 もっと正確に言えば、あなたは語り始めることができます。 彼が最後に耳を傾けることはまずありません。 そして、彼は原則として正しいでしょう。これは全く普通の、目立たない式です。 ブラーリ・フォルティの議論では、彼女は中心的な場所を占めることはなかったが、パラドックスの定式化のほんの一瞬でした。 彼女の罪悪感はすべて、ポアンカレの目を引いたという事実にあります。ポアンカレは、彼女の中に「ブレースの延長」という望ましくない哲学的意味を見ました。 地獄のような外観については、フレーゲの表記法は100ポイントのハンディキャップを与えます。
参照資料
ここでは、言及された本へのリンクを掲載したいのですが、義人の努力のおかげで、あらゆる種類の不明瞭な場所、疑わしいファイルホスティングサービス、ed2kネットワークからそれらをダウンロードしなければなりませんでした...そして興味深い読書。 ファン・ヘイノルトによる「フレーゲからゲーデルへ」も非常に好奇心が強いが、理解するのは難しく、ロシア語では存在しないようだ。
ポストスクリプト
最近のイベント(「鉄」ハブのティックタイムへの移行)に照らして、ハブハブのトピックに直接関連しない小さな調査を実施したいと思います。 この自由を許してください。