内容
- テンソルとは何ですか、なぜ必要ですか?
- ベクトル演算とテンソル演算。 テンソルランク
- 曲線座標
- テンソル博覧会のポイントのダイナミクス
- テンソルのアクションとその他の理論的な質問
- 自由固体の運動学。 角速度の性質
- ソリッドの最終回転。 回転テンソルのプロパティとその計算方法
- Levi-Civitaテンソルの畳み込みについて
- 最終回転のパラメーターによる角速度テンソルの導出。 頭とマキシマを適用
- 角速度ベクトルを取得します。 欠点に取り組む
- 自由な動きでの体のポイントの加速。 ソリッドの角加速度
- 固体運動学におけるロドリゲハミルトンパラメーター
- テンソル式の変換の問題におけるSKA Maxima。 ロドリゲ・ハミルトンのパラメーターにおける角速度と加速度
- 剛体のダイナミクスの非標準的な紹介
- 非自由な固体運動
- 固体の慣性テンソルの特性
- ナットジャニベコバのスケッチ
- ヤニベコフ効果の数学的モデリング
はじめに

今回の紹介は「アクティブ」です。 すぐに作業を開始し、前の記事6および9の結果を使用して、固体の角速度の擬似ベクトルを取得し、最終回転のパラメーターで表現します。
そのため、Maximaでの長い手動の苦痛と短いが骨の折れる変換によって、ランク2の非対称角速度テンソルは次のように見えるという結論に達しました。
Levi-Civitaテンソルで(1)を折り畳むことにより角速度の擬似ベクトルを取得する方法について話しました。
しかし、さらなる研究により、式(2)には誤った結果につながるエラーが含まれていることが示されました。 解決策は、文献を研究し、Levi-Civitaテンソルの畳み込みに関する記事の結果をさらに理解することで見つかりました。
その結果として起こったことに興味のある人を猫に招待します。
ペーパーワークに煩わされることはありません。Maximaを使用し、バッチファイルに「設定」します
omega.mac
kill(all); load(itensor); imetric(g); idim(3); <p>depends([u,phi],t);</p> <p>Omega:ishow( (1-cos(phi))*(diff(u([m],[]),t)*u([k],[]) - u([m],[])<em>diff(u([k],[]),t)) + sin(phi)</em>(1-cos(phi))<em>u([],[i])</em>('levi_civita([i,l,k],[])*diff(u([],[l]),t)*u([m],[]) - 'levi_civita([i,j,m],[])*diff(u([],[j]),t)*u([k],[])) + sin(phi)<em>cos(phi)<em>diff(u([],[p]),t)</em>'levi_civita([m,p,k],[]) + diff(phi, t)</em>'levi_civita([m,q,k],[])*u([],[q]))$</p> <p>Omega2:ishow(expand(lc2kdt('levi_civita([],[m,k,r])*Omega)))$</p> <p>Omega3:ishow(canform(contract(expand(Omega2))))$</p>
結果を得る

この式を手動で確定した後、真実に非常に類似した結果が得られます
ここでのみ(3)正確に2倍以上の真実-回転軸を動かさずに置くと、
つまり、角速度は回転軸に沿って向けられますが、回転角の微分の2倍です。 これはどのようにできますか? これは不可能であり、不正確は定義(2)で行われます。 この不正確さの理由、反対称テンソルと擬似ベクトルに関するアイデアの改良が、この記事の目標です。
1.再びランク2の反対称テンソルの付随するベクトルについて
角速度テンソルを考慮します(1)。 それは反対称なので、誰も私たち自身でそれを分解することを気にしません
結果(4)は、角速度テンソルの反対称性に基づいています(
そして今注目-ベクトルを導入します
そして、このベクトルから再びテンソルを取得できることは明らかです(1)
(4)に完全に従っています。 そして今、(6)、はじめに(1)で行ったことを行います-レビ-チビタ反変テンソルでロールアップします
それで、デュースがありました-実際、角速度テンソルをLevi-Chevita反変テンソルで折り畳むと、1つではなく2つの角速度が得られます。 5番目の記事では、付随するベクトルを取得するために関係(2)が与えられ、Levi-Civitaテンソルの乗算と畳み込みの規則が無視されたため、導入で得られた結果は誤りです。 計量テンソルの場合のように、逆変換の場合、式の右側と左側に逆テンソルを掛けるだけで十分です。 しかし、それとは逆のインデックスのペアで畳み込むときのメトリックテンソルのみがクロネッカーデルタを与えますが、インデックスのペアのペアで畳み込むときのLevi-CivitaテンソルはTWOクロネッカーデルタを与えます。 これがエラーの理由であり、結果の表示は2倍でした。
付随する擬似ベクトルを取得するには、関係(5)を使用する必要があります。 次に、角速度の正しい結果に到達します
さて、(8)を取得するには、少し時間を費やす必要がありました。 したがって、 8番目の記事では、Levi-Civitaテンソルの特性にそのような注意が払われました。 5番目と6番目の記事はそれに応じて修正されます。
間違いを犯すことは、私の出版物をフォローしている聴衆を考えると、非常に迷惑です。 ただし、このサイクルの記事では、テンソル計算とそれを実際の問題の解決に適用する方法の説明に加えて、私の特定の例を使用して認知のプロセスも説明しています。 そして、ご存知のように、認知のプロセスは多くの反復で構成されています。
最終的に、目標に到達しました-さらに、非縮退メトリックを持つ任意の座標について、最終回転のパラメーターに関して角速度の式を取得しました。
2.なぜまだ擬似ベクトルなのですか?
それで、角速度を取得しました。 簡単にするために、体の回転軸がその方向を変えないと仮定します。 次に、式(8)は自明な形式になります
角速度ベクトルの古典的な定義を示しています
角速度ベクトルは、回転軸に沿って、反時計回りに回転が発生するように見える方向に向けられます。
なぜ反時計回りですか? 理論力学、物理学、数学のコースを設定するとき、デフォルトの座標系がデフォルトで使用されるためです。 反時計回りに正の回転方向を持っています。
(9)に目を向けます。 回転角の導関数の正の値は、角度が時間とともに増加することを示しています。 これは、回転が正方向であることを意味します。つまり、
そしてここでも-速度ベクトルは、角速度から半径ベクトルへの最短回転が正方向、つまり反時計回りに発生するように見える方向に向けられます(図1)。

図 1.剛体の回転-正しい座標系
次に、座標系を左に変更します(図2)
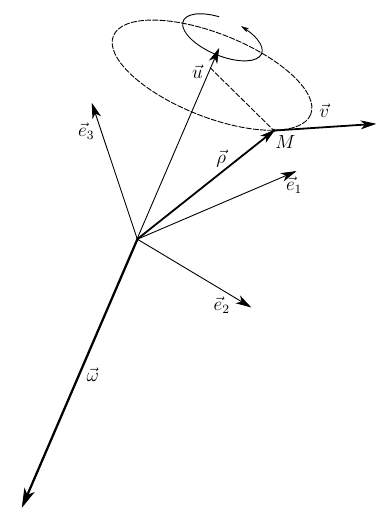
図 2.剛体の回転-左座標系
身体は、どの座標系でそれを考慮するかを気にしません。 回転した場所で回転します。 ただし、新しいシステムの基準回転角の正方向は時計回りです。 したがって、身体の既存の回転方向では、回転角度が減少し、
体の先端の速度はどうなりますか? しかし、何もありません-(10)によれば、ベクトルは、角速度から半径ベクトルへの最短回転が時計回りに発生するように見える場所に向けられます。これは、新しい座標系でそのような正の方向が選択されているためです。 これは、ボディポイントの速度ベクトルの方向が同じままであることを意味します。
右の座標系から左へ、またはその逆に移動するとき、つまり基底の向きを変更すると、角速度ベクトルの方向が変わることがわかります。 したがって、不可欠な幾何学的オブジェクトとして、基底の変更に対して不変ではありません。 そのようなベクトルは、 疑似ベクトルと呼ばれます 。 それらは軸ベクトルとも呼ばれ、事実を強調します。ベクトルの方向は、この座標系で選択された正の回転方向によって決まります。
反対に、速度ベクトルは、基底の向きを変更しても方向を変えず、 真または極ベクトルと呼ばれます 。
真のベクトルのベクトル積の結果は、軸ベクトルです。 しかし、なぜ(10)は真のベクトルを与えるのでしょうか? ただし、引数の1つは軸方向ベクトルであり、左の座標系に移動するときに方向を変更すると、ベクトル積の方向の変更がなくなります。 したがって、疑似ベクトルと真のベクトルのベクトル積は、真のベクトルを生成します。
この意味で、角速度ベクトルはやや不便です。 したがって、固体力学のテンソル関係を導出するときは、座標系の任意の変換に関して不変の角速度テンソルに依存する方が適切です。
3.少しの練習-角速度テンソルからのオイラーの運動方程式の導出
読者が面倒な公式に飽きさせず、得られた関係の実際的な価値を理解できるように、体の回転の任意のパラメーターを通じて角速度の成分の表現を取得する方法の例を示します。 たとえば、オイラー角を通して。
デカルト右座標系で作業します。 オイラー角を使用すると、図3に示すように、空間内の剛体の任意の方向を指定できます。

図 3.オイラー角-軸z、x、zの周りの接続された座標系の順次回転
身体の任意の方向は、3つの連続した回転によって取得できます。
これは、デカルト座標の回転行列が、z、x、z軸の周りの回転の線形変換の合成のように見えることを意味します
次に、(11)それらの式の1つに適用して、回転テンソルを取得します。
デカルトベースで作業するため、計量テンソルは単位行列で表されます。 SKAを使用した微分と行列乗算の実行(このようなコマンドを使用したMapleなど)
restart; <p>with(LinearAlgebra):</p> <p>A01 := Matrix( [ [cos(psi(t)), -sin(psi(t)), 0], [sin(psi(t)), cos(psi(t)), 0], [0, 0, 1] ]);</p> <p>A12 := Matrix( [ [1, 0, 0], [0, cos(theta(t)), -sin(theta(t))], [0 ,sin(theta(t)), cos(theta(t))] ]);</p> <p>A23 := Matrix( [ [cos(phi(t)), -sin(phi(t)), 0], [sin(phi(t)), cos(phi(t)), 0], [0, 0, 1] ]);</p> <p>B := A01 . A12 . A23;</p> <p>dBdt := map(diff, B, t);</p> <p>Omega := map(simplify,B^(-1) . dBdt, trig);</p>
回転テンソル行列を取得します
(12)から、身体に関連付けられた座標系の角速度の成分を取得するのは簡単です
力学の専門家は、(13)-(15)で、角速度ベクトルを体の回転のパラメーターと関連付けるオイラー運動方程式を確実に学習します。
同様に、角速度は任意の回転パラメーターに関連付けることができます。 角速度を最終回転のパラメーターに関連付けることにより、一般的な方法で式(8)を得るためにすべての変換を行いました。 ただし、表現(8)も表現(13)-(15)も、剛体の運動の動的解析には便利ではありません。上記の式はパラメータの特定の値に対して縮退するためです。 将来的には、(8)を使用して、縮退の影響を受けない四元数成分で表される角速度に移動します。 そして、この例はテストであり、実例です。
おわりに
この注記の大部分は、以前の出版物で行われたエラーおよび不正確性に関する作業です。 しかし、結果は達成されました-最終回転のパラメーターを介して体の角速度ベクトルの定義を得て、角速度が擬似ベクトルであることを明確に示しました。
ご清聴ありがとうございました!
継続するには...