Clever Geek Handbook

ミュラーの再発率：浮動小数点数の丸めに関する問題

少し前に、それほど難しくない運動に出くわしました。



シーケンスx nを次のように定義します。



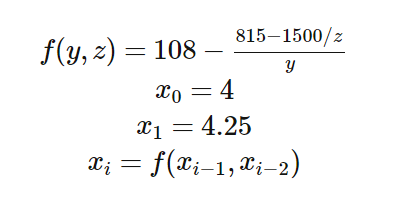
カウントx 30 。



コーディングはそれほど難しくなく、おそらくx iを再帰関数として実現します。 通常の倍精度浮動小数点数では、 iが増加すると、結果は100にうまく収束します。



残念ながら、100は正解ではありません。 実際、シーケンスは5に収束します。



問題



このシーケンスはミュラー回帰比として知られており、特に浮動小数点エラーが適切な（まあ、間違った）条件で悲惨な結果をもたらすことをいかに迅速かつ劇的に丸めるかを示すために合成されました。 このペーパー（pdf）では、丸めのさまざまな危険性、特にこのシーケンス（p。14）について詳しく調べています。 問題の別の説明はこちら（pdf）にあります。



私を含む多くのプログラマーは、状況によっては浮動小数点数の数学が間違っている可能性があることを認識していると思いますが、計算に非常に大きな数または非常に小さな数が関係している場合にのみ発生する可能性があると信じて問題を却下します膨大な数のエラーが蓄積されます。 無邪気な見た目の定数と少数の反復によるこの演習は、丸め誤差が極端な数に加えて重大な影響を与える可能性があることを完全に示しています。 この場合、固定点5の不安定性は、小さなエラーでさえ結果を大きく変えるという事実につながります。



他には何も追加できませんが、この問題は共有する価値があると思います。



正しい結果の計算



Mathematicaの短いプログラムを使用して、通常の浮動小数点数と任意精度の演算の間でシーケンスの最初の100個の値を比較できます。 便利な数学メモ化構文を使用しているため、100回以上反復しても計算は非常に高速です。



f [ y_ 、z _ ] ：= 108- （ 815-1500 / z） / y;



xExact [ 0 ] = 4 ;

xExact [ 1 ] = 17/4 ;

xExact [n _ ] ：= xExact [n] = f [ xExact [n - 1 ]、 xExact [n - 2 ]];



xFloat [ 0 ] = 4 ;

xFloat [ 1 ] = 4.25 ;

xFloat [n _ ] ：= xFloat [n] = f [ xFloat [n - 1 ]、 xFloat [n - 2 ]];



TableForm [

テーブル [{i、 N [ xExact [i]、 20 ]、 N [ xFloat [i]、 20 ]}、{i、 0、100 }]、

TableHeadings- >

{ なし 、{ "i" 、 "x [i] \" exact \ "" 、 "x [i]浮動小数点" }}

結果： 
 ix [i] "exact" x [i]浮動小数点
 -------------------------------------------------- -
 0 4.0000000000000000000 4.0000000000000000000
 1 4.2500000000000000000 4.25
 2 4.4705882352941176471 4.47059
 3 4.6447368421052631579 4.64474
 4 4.7705382436260623229 4.77054
 5 4.8557007125890736342 4.8557
 6 4.9108474990827932004 4.91085
 7 4.9455374041239167248 4.94554
 8 4.9669625817627005987 4.96696
 9 4.9800457013556311613 4.98004
 10 4.9879794484783922601 4.98791
 11 4.9927702880620680975 4.99136
 12 4.9956558915066340266 4.96746
 13 4.9973912683813441129 4.42971
 14 4.9984339439448169190 -7.81676
 15 4.9990600719708938678 168.943
 16 4.9994359371468391480 102.04
 17 4.9996615241037675378 100.1
 18 4.9997969007134179127 100.005
 19 4.9998781354779312492 100。
 20 4.9999268795045999045 100。
 21 4.9999561270611577381 100。
 22 4.9999736760057124446 100。
 23 4.9999842055202727079 100。
 24 4.9999905232822276594 100。
 25 4.9999943139585595936 100。
 26 4.9999965883712560237 100。
 27 4.9999979530213569080 100。
 28 4.9999987718123113300 100。
 29 4.9999992630872057846 100。
 30 4.9999995578​​522583059 100。
 31 4.9999997347113315242 100。
 32 4.9999998408267904691 100。
 33 4.9999999044960712411 100。
 34 4.9999999426976416502 100。
 35 4.9999999656185845961 100。
 36 4.9999999793711506158 100。
 37 4.9999999876226903184 100。
 38 4.9999999925736141727 100。
 39 4.9999999955441684970 100。
 40 4.9999999973265010958 100。
 41 4.9999999983959006566 100。
 42 4.9999999990375403937 100。
 43 4.9999999994225242361 100。
 44 4.9999999996535145416 100。
 45 4.9999999997921087250 100
 46 4.9999999998752652350 100。
 47 4.9999999999251591410 100。
 48 4.9999999999550954846 100。
 49 4.9999999999730572908 100。
 50 4.9999999999838343745 100。
 51 4.9999999999903006247 100。
 52 4.9999999999941803748 100。
 53 4.9999999999965082249 100。
 54 4.9999999999979049349 100。
 55 4.9999999999987429610 100。
 56 4.9999999999992457766 100。
 57 4.9999999999995474659 100。
 58 4.9999999999997284796 100。
 59 4.9999999999998370877 100
 60 4.9999999999999022526 100。
 61 4.9999999999999413516 100。
 62 4.9999999999999648110 100。
 63 4.9999999999999788866 100。
 64 4.9999999999999873319 100。
 65 4.9999999999999923992 100。
 66 4.9999999999999954395 100。
 67 4.9999999999999972637 100。
 68 4.9999999999999983582 100。
 69 4.9999999999999990149 100。
 70 4.9999999999999994090 100。
 71 4.9999999999999996454 100。
 72 4.9999999999999997872 100。
 73 4.9999999999999998723 100。
 74 4.9999999999999999234 100。
 75 4.9999999999999999540 100。
 76 4.9999999999999999724 100。
 77 4.9999999999999999835 100。
 78 4.9999999999999999901 100。
 79 4.9999999999999999940 100
 80 4.9999999999999999964 100。
 81 4.9999999999999999979 100。
 82 4.9999999999999999987 100。
 83 4.9999999999999999992 100。
 84 4.9999999999999999995 100。
 85 4.9999999999999999997 100。
 86 4.9999999999999999998 100。
 87 4.9999999999999999999 100。
 88 4.9999999999999999999 100。
 89 5.0000000000000000000 100。
 90 5.0000000000000000000 100。
 91 5.0000000000000000000 100。
 92 5.0000000000000000000 100。
 93 5.0000000000000000000 100。
 94 5.0000000000000000000 100。
 95 5.0000000000000000000 100。
 96 5.0000000000000000000 100。
 97 5.0000000000000000000 100。
 98 5.0000000000000000000 100。
 99 5.0000000000000000000 100。
 100 5.0000000000000000000 100。




More articles:


All Articles