HRV分析は、ECR RR間隔のシーケンスの決定に基づいています。 2つの連続した心臓収縮の間。 また、NN間隔(正常から正常へ)の概念も使用します。つまり、ここでは正常な収縮の間隔のみが考慮されます(分析では、心臓のリズム障害の場合に記録された間隔、および外部干渉から生じる間隔は考慮されません)。

図の上のグラフは、ECGによってRR間隔の期間を検出するプロセスを示しています。
検査後、患者は心間隔図(CIG)を受け取ります。これはRR間隔のセットです(図の下のグラフ、次々に表示されます。ここで、パルスの高さはmsでの対応するRR間隔の持続時間に等しく、次のパルスが現れる瞬間はその検出時間に対応します)
現在、HRVを評価する方法はいくつかあります。 次の3つのグループが区別されます。
- 時間領域法-統計的手法に依存し、一般的な変動性の研究を目的としています。
- 自己相関分析と相関リズモグラフィー-HRVの不可欠な指標。
- 周波数領域法-HRVの周期成分の研究。
この点で、HRVの分析のためのさまざまな方法は、異なる定性的および定量的評価基準を使用します。 心拍数を評価するためのさまざまな方法に基づいて取得されたデータの解釈に矛盾がある場合があります。 したがって、関連する方法は、HRV指標の総合評価です。 R. つまり HRVの定性分析は3つすべての方法で実行する必要があり、取得したデータを使用してPARSインジケーターを計算します。
分析の初期データは、次のR波の出現の連続する瞬間の記録です。 5分間の記録は分析によく使用されますが、異なる期間の記録を分析するオプションがあります。
CIGを構築するには、ECGにR波が現れる瞬間だけでなく、2つの隣接するR波の間の時間の長さも知る必要があります。 この期間を計算するには、最終的な差異を計算するMATALAB diff関数を使用します。
RR = diff(D_times); % RR-. D_times – R-, times = D_times(2:(length(D_times))); % .
次に、正常ではない可能性のあるRR間隔を決定します(NN間隔を取得します)。 これを行うには、最初に各RR間隔のフラグ値の単位ベクトルを作成します。
flags = ones(max(size(RR)),1); % RR-.
ここで、「異常な」RR間隔に対応するフラグベクトル(フラグ)の要素をゼロで置き換えます。 さらに、異常な間隔を手動で特定する必要があります。
これを行うには、stem関数を使用して、調査対象の信号のCIGを作成します。
stem (RR, 'Marker','.', 'color', [0 0 0]), title (' ', 'FontSize', 12); xlabel(' ','FontSize',12); ylabel(', .','FontSize',12);

この図は、異常な(洞調律に関係しない)間隔を持つ構造の断片を示しています。この値は、以降の計算では考慮できません。
このような間隔はCIGから削除され、それらの削除の領域は、隣接する間隔のサイズに応じて線形法によって補間されます。 このアプローチにより、信号の全体的なダイナミクスを乱すことなくNNシーケンスを作成できます。 ただし、CIG分析の結果は、誤った間隔の値が5〜6以下で十分であることに注意する必要があります。
削除された間隔を復元するには、MATLAB関数を使用して1次元のテーブル内挿を行います。 構文:
RRinterp = interp1(x、y、xi、 '<method>')。
この場合、x-偽(または偽のグループ)間隔の近傍の発生時間、y-持続時間、xi-フラグでマークされた偽の間隔の発生時間、 '<method>'-'linear'を取ります。 その結果、RRinterp変数は、補間された間隔の期間を返します。

次のステップで、図を取得する必要があります 3スムーズ補間法を使用して均一にサンプリングされた信号。 これを行うには、3次スプライン補間を使用することをお勧めします。 均一サンプリングの推奨サンプリングレートは4 Hzです。
fInt = 4; % / xSpline = min(times): 1/fInt: max(times); % / RRspline = interp1(times, RRint, xSpline, 'spline'); % . times – , RRint – NN-.
処理されたRIGspline CIG信号の周波数分析を行うには、その定数成分を取り除く必要があります。 線形トレンドを削除します。 これは、サンプルからRRspline信号の算術平均を減算することにより実現されます。
RRdetrend = RRspline-平均(RRspline);
結果を図に示します。

周波数分析(パワースペクトル密度の計算)を実行するには、離散フーリエ変換(DFT)手順を実行する必要があります。 この場合、スペクトル漏れとくし形歪みを最小限に抑える必要があります。 これを行うには、ウィンドウ計量方法を適用します。 25%のスムージングでTukeyウィンドウを使用することをお勧めします。
w = tukeywin(length(rrdetrend), 0.25); % 25% . rrdetrend = (w'.*rrdetrend).*1000; % .
また、ゼロの補数を実装します。
Pspectr = fft(rrdetrend, 2048); % 2^11.
FFTアルゴリズムに基づいて計算された調査対象のCIG信号のPSDの計算結果を図に示します。
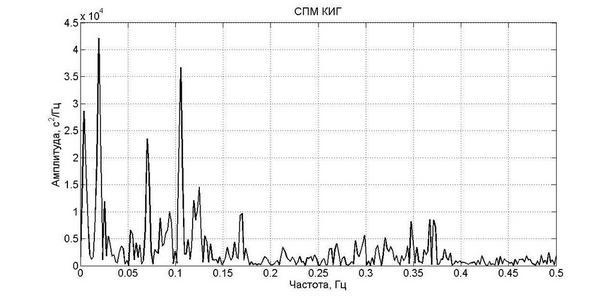
ここでは、FFTを使用するピリオドグラム法について説明します。 それに加えて、ウェルチ法、自己回帰などがあります。
取得したデータに基づいて、HF、LF、VLF信号成分のパワー、およびTRの合計パワーを計算します。 推奨事項に従って、範囲は次の周波数に制限されます。
BW = [0.003 0.04; ... % , VLF 0.04 0.15; ... % , LF 0.15 0.4]; % , HF
コンポーネントのパワーを計算するには、trapz関数を使用します。 関数I = trapz(y)は、積分ステップが一定でユニティに等しいと仮定して積分を計算します。 ステップhがユニティではなく一定である場合、計算された積分にhを掛けます。 この場合、h =(fInt / N)、ここでfInt = 4 Hzはサンプリング周波数、Nは計算されたFFTビンの数です。
得られたデータは、よく知られた式に従ってPARSの周波数パラメータを計算するのに十分です。
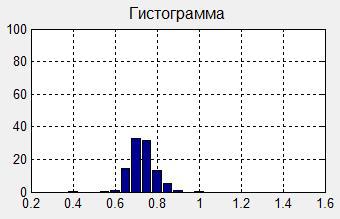
ヒストグラムの幾何学的パラメーターを定義します。 これを行うには、推奨事項に従って、心臓間隔のグループ化の範囲が示され、histコマンドが使用されます。
dRR = 0.4: 0.05: 1.3; % [ampRR, dRR] = hist (RRspline, dRR); % ampRR_proc = (ampRR.*100)./length(rrspline); % [yMo, yi] = max (ampRR); Mo = dRR(yi); % - AMo = (yMo*100)/length(RRspline); % MxDMn = (max(RRspline) - min(RRspline)); % bar (dRR, ampRR_proc), grid on % . title ('', 'FontSize', 12); ylabel('%','FontSize',12); axis ([0.2 1.6 0 100])
構築の結果を図に示します。
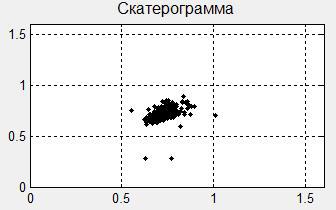
スキャッタグラムを作成しています。
rr1 = RRspline (1 : 2:end); % () RR(n) rr2 = RRspline (2 : 2: end); % () RR(n+1) if length(rr1) ~= length(rr2) if length(rr1) > length(rr2) rr1 = rr1 (1: end - 1); else rr2 = rr2 (1: end - 1); end end plot (rr1, rr2,'Marker','.','LineStyle','none','Color',[0 0 0]) title ('', 'FontSize', 12), grid on axis ([0 1.6 0 1.6])
PS:私は医療の専門家ではないので、不正確な点を認めます。
説明された分析原理は、私が発見した情報源に基づいて登場し、すでにパブリックドメインで利用可能になっています。
このジャンルの特性により、マテリアルは簡潔であり、MATLABのいくつかの技術的な側面を省略しようとしました。
私は建設的な批判に喜んで、可能な質問に答えようとします。 この資料が誰かに役立つことを願っています。 ご清聴ありがとうございました!
ソース
十分にアクセス可能で、研究方法に関する主なもの
バエフスキーRM et al。さまざまな心電図システムを使用した心拍変動の分析
HRV分析の測定基準と推奨事項
PhysioNet RR間隔データベース
すぐに使用できるMATLAB機能:心拍数変動のためのソフトウェア