ソフトウェアレンダラー-2：属性のラスタライズと補間

こんにちは 前の記事で、グリッドの形式で画面上に3次元のシーンを表示するために必要な数学について説明しました。 スクリーン空間の頂点の座標を取得した時点で停止しました。 次のステップは、オブジェクトを構成するポリゴンを「塗りつぶす」ことです。 画面上のオブジェクトの画像に含まれるピクセルを検索します。 これらのポイントを見つけるプロセスは、ラスタライズと呼ばれます。 また、オブジェクトをテクスチャリングおよび照明できるようにしたいため、頂点で指定された属性（テクスチャ座標、法線、色など）を補間できる必要があります。



入力は多角形のセットです（三角形のみを考慮します）：頂点の座標（座標系はアルゴリズムに依存します）およびこれらの各頂点の属性値は、三角形の表面に沿ってさらに補間されます。 この記事では、いくつかの落とし穴について説明します。

• ピクセル塗りつぶしルール
• 精度
• 属性補間中の遠近補正（遠近補正内挿）

ラスタライズへの3つのアプローチを検討します。

• 顔の傾きを使用する「標準」アルゴリズム
• 多角形の面の方程式（トラバーサルアルゴリズム）の使用に基づく多数のアルゴリズム
• 均一なラスター化アルゴリズム

また、最後に、実装例であるプロジェクトへのリンクがあり、そこからコード例もあります。

基本

したがって、ラスタライズは、特定のポリゴンに「含まれる」ピクセルを見つけるプロセスです。 まず、ポリゴンを単色で塗りつぶすだけで十分だと仮定します。



画面に表示するための次の三角形があると想像してください（すべての座標は既に画面スペースに表示されています）。







どのピクセルを塗りつぶす必要がありますか？ ピクセルは、完全にポリゴンの外側、部分的にポリゴン内、完全にポリゴン内にあります。







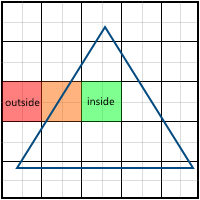
次の2つの場合、すべてが簡単です。

• ピクセルはポリゴン全体に含まれていません（写真の赤い色）-塗りつぶさないでください
• ピクセルはポリゴン全体に含まれています（図の緑色）-塗りつぶします

3番目のケース（ピクセルは部分的にポリゴンの内側にあります）はより複雑です。 頭に浮かぶ最初の決定は、そのようなピクセルがすべてポリゴンに含まれるかどうかを想定することです。 しかし、それは間違った結果につながります。 描画する3次元モデルは多くの三角形で構成されており、通常は互いに重ならないようにします。 互いに重なり合う三角形は、既存の情報を複製するだけなので、意味がありません。 したがって、多くのポリゴンには共通の面があります。 最も簡単な例は長方形です：







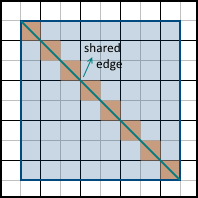
両方のポリゴンに部分的に収まるピクセルは、オレンジ色でマークされています。 これら両方のポリゴンをラスタライズするとします。 ポリゴンに部分的に含まれるすべてのピクセルを塗りつぶす必要があると判断した場合、同じピクセルを2回取得します（3つ以上のポリゴンに共通の頂点がある場合はさらに多くなります）。 これは一見問題に思えないかもしれませんが、実際には、アルファブレンディング（透明度をシミュレートするためにアルファチャネルを使用してレンダリング）などのいくつかの手法を使用すると、さまざまなアーティファクトが発生します。 これは生産性の低下にもつながります。なぜなら、 属性値を計算する必要があるピクセルの数は増加しています。 反対に、そのようなピクセルが最終画像に含まれておらず、塗りつぶしてはならないと判断した場合、ポリゴン間に「穴」ができますが、これは受け入れられません。



したがって、隣接するポリゴンを描画するとき、各ピクセルを1回だけ塗りつぶす必要があるということがわかりました。 これは、Direct3DとOpenGLの両方が準拠する要件です。



問題は、連続（画面の座標系）から離散（モニター上のピクセル）に表示する必要があるために発生します。 従来のラスタライズアルゴリズム（スムージングなしでレンダリングする場合）は、これを次のように解決します。各ピクセルは、ポリゴンに入るピクセルの原因となる特定のポイント（サンプルポイント）に関連付けられます。 また、この時点で、必要なすべての属性の値が考慮されます。 言い換えれば、画面の座標系でピクセルが占めるすべての空間は、1つの点で「表されます」。 原則として、これは中心です：（0.5、0.5）：







理論的には、ピクセルの中心ではなく、ピクセル内の任意のポイントを取ることができます。 他の値は、画像を一方向に1ピクセルずつ「シフト」できるという事実につながります。 また、隣接するポリゴンがある状況では、三角形の頂点が配置されていないピクセルの場合、ポイント（0.5、0.5）の使用には良い特性があります：このポイントは、ピクセルを表す長方形の面積の50％以上をカバーするポリゴンに含まれます。



したがって、ピクセルの中心がポリゴンに入る場合、ピクセルはポリゴンに属すると見なされます。 しかし、次の問題が発生します。2つのポリゴンにピクセルの中心を通る共通の面がある場合はどうでしょうか。 ピクセルは2つの三角形のうちの1つだけに属している必要があることにすでに気付きましたが、どちらが三角形ですか？ 以下の図では、そのようなピクセルは赤でマークされています。







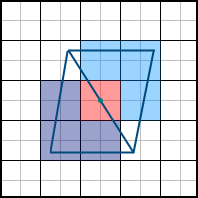
この問題は、いわゆる「充填規則」によって解決されます。

充填契約

したがって、上記の状況に直面していると仮定します。2つのポリゴンは、ピクセルの中心を正確に通過する面を共有します。 私たちのタスクは、このピクセルがどのポリゴンに属しているかを調べることです。



事実上の標準は、いわゆる左上ルールです。DirectXおよびほとんどのOpenGL実装に従います。 このルールの本質は次のとおりです。ポリゴンの面がピクセルの中心を通過する場合、このピクセルは2つの場合にポリゴンに属します-左側または上面の場合（名前の由来）。



左、右、上面、および下面の概念を明確にする必要があります。 これまでのところ、正確な定義は行いません（トラバーサルアルゴリズムに到達したらこれを行います）が、より単純な言語でそれらを説明します。

• 上面は、他のすべての面の上にある水平面です
• 下-他のすべての面の下にある水平面
• 左側-三角形の左側にあり、水平ではない面
• 右側は、三角形の右側にあり、水平ではない面です

例：







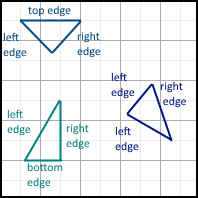
次に、隣接するポリゴンの場合を考えます。 面が隣接し、1つのポリゴンに残っている場合、この面をこのポリゴンと共有するすべてのポリゴンに対して同じ面が正しいです。 同様の規則は、上面と下面に対して機能します。







このプロパティを使用して、ピクセルが隣接するポリゴンのどれに属するかを判断できます。 中心が共通の面にあるピクセルが、この面が残っているポリゴンのみに属することに同意する場合、この面は正しいため、隣接するポリゴンには自動的に属しません。 上限についても同じです。



上面と左側の面の規則が最も頻繁に見つかるという事実にもかかわらず、適切な組み合わせを使用できます。 たとえば、下側と左側、上側と右側などのルール。 Direct3Dでは左上のルールを使用する必要がありますが、OpenGLはそれほど厳密ではなく、ピクセル所有権の問題を解決するルールを使用できます。 引き続き左上のルールを使用することを想定します。

精度

次の2つのポリゴンを検​​討してください。







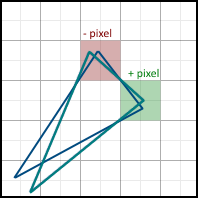
特定の角度での回転の結果として、最初のポリゴンから2番目のポリゴンを取得できます。 結果として、いくつかのピクセルが最終画像に追加で含まれ（そのようなピクセルは緑色でマークされます）、反対に、いくつかはピクセルから消えます（赤色でマークされます）。 したがって、頂点座標の小数部分を考慮する必要があります。 それらを破棄すると、静的でないシーンを描画するときに問題が発生します。 たとえば、ポリゴンを非常にゆっくりと回転させると、中間結果を正しく処理する代わりに、エッジがある位置から別の位置に急激に「ジャンプ」するため、動きがぎくしゃくします。 これらの2つの動画を比較すると、違いを簡単に理解できます。









もちろん、静的なシーンの場合、このような問題は発生しません。

属性補間

ラスタライズアルゴリズムに直接進む前に、属性の補間について詳しく見てみましょう。



属性は、オブジェクトに関連付けられた情報です。これは、特定のアルゴリズムに従って正しいレンダリングを行うために必要です。 何でもそのような属性になり得ます。 最も一般的なオプションの1つは、色、テクスチャ座標、法線座標です。 属性値は、オブジェクトグリッドの頂点で設定されます。 ポリゴンをラスタライズする場合、これらの属性は三角形の表面に沿って補間され、各ピクセルの色を計算するために使用されます。



最も単純な例（および「hello world」の独特な類似物）は、三角形の描画であり、各頂点に1つの属性が与えられています-色：







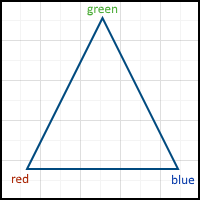
この場合、3つの頂点の色の線形補間の結果であるポリゴンの各ピクセルに色を割り当てると、次の画像が得られます。







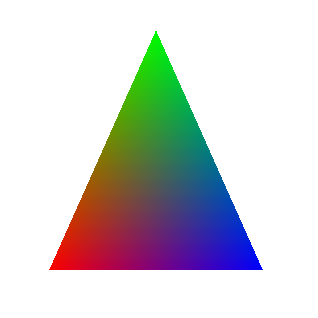
補間が行われる方法は、レンダリングプロセスで操作するデータに依存し、それらは、ラスタライズで使用されるアルゴリズムに依存します。 たとえば、「標準」アルゴリズムを使用する場合、2つのピクセル間の値の単純な線形補間を使用できます。また、トラバーサルアルゴリズム-重心座標を使用する場合も使用できます。 したがって、アルゴリズム自体の説明まで延期します。



ただし、前もって対処する必要がある重要なトピックがまだあります。遠近補正による属性補間です。



最も単純な補間方法は、画面空間での線形補間です。ポリゴンが投影面に投影された後、三角形の表面に沿って属性を線形補間します。 この補間は実行される投影を考慮しないため、この補間は正しくないことを理解することが重要です。



投影面d = 1に線を投影することを検討してください。 開始ピークと終了ピークで、カメラ空間（および世界）で線形に変化する特定の属性が設定されます。 投影が行われた後、これらの属性は画面空間で直線的に成長しません。 たとえば、カメラ空間の中間点（ v = v0 * 0.5 + v1 * 0.5 ）を取得した場合、投影後、この点は投影された線の中央にありません。







これは、オブジェクトをテクスチャリングするときに最も簡単に気付きます（以下の例では、フィルタリングせずに単純なテクスチャリングを使用します）。 テクスチャリングプロセスについては詳しく説明していません（これは別の記事のトピックです）ので、ここでは簡単な説明に限定します。



テクスチャリングの際、ポリゴンの各頂点で、テクスチャ座標の属性の値が設定されます（多くの場合、対応する軸の名前でuvと呼ばれます）。 これらは、テクスチャのどの部分を使用するかを決定する正規化された座標（ 0〜1 ）です。

ここで、テクスチャ化された長方形を描画し、テクスチャ全体が使用されるようにuv属性の4つの値を設定することを想像してください。







すべてがうまくいくようです：







確かに、このモデルは投影面に平行に配置されているため、遠近法による歪みはありません。 上の2つの頂点をz軸に沿って1つずつシフトしようとすると、問題がすぐに明らかになります。







したがって、属性を補間するときはパースペクティブを考慮する必要があります。 これの重要な事実は、 zを画面空間で正しく補間することはできませんが、 1 / zはできることです。 繰り返しますが、線の投影を検討してください。











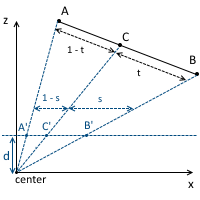
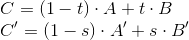
また、同様の三角形によってそれをすでに知っています。







スクリーン空間でxを補間すると、次のようになります：







カメラ空間でxを補間すると、次のようになります。







これらの3つの等式が重要であり、それらに基づいてすべての後続の式が導出されます。 私はこれを自分で簡単に行うことができるため、完全な結論を出すことはせず、結果に焦点を当てて簡単に説明します。



これらの2つの等式を三角形のアスペクト比から取得した方程式に代入し、すべての式を単純化すると、最終的にz座標の逆数を画面空間で線形補間できることがわかります。







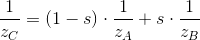
この式では、チャンバー空間のz座標の逆数の間で補間が行われることが重要です。



さらに、特定の属性の値が頂点AおよびBに設定されていると仮定し、それらをT1およびT2で示します。これらはカメラ空間でも線形補間できます。







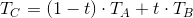
上記の出力の中間結果を使用して、 Tc / Zcの値もスクリーン空間で正しく補間できることを記述できます。







まとめると、 1 / ZcおよびTc / Zcはスクリーン空間で線形補間できることがわかりました。 これで、 Tcの値を簡単に取得できます。







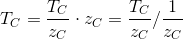
実際、前向きに正確な補間のコストは主にこの区分にあります。 あまり必要でない場合は、使用する属性の数を最小限に抑え、可能であれば画面空間での単純な線形補間を行わない方が良いでしょう。 正しいテクスチャリング結果を以下に示します：







遠近補正を実装するには、カメラ空間の頂点の深さ（ z座標）に逆の値が必要です。 射影行列を掛けると何が起こるか思い出してください：







カメラ空間からの頂点はクリッピング空間に入ります。 特に、 z座標は特定の変更（将来的に深度バッファに必要となる）を受け、カメラ空間の頂点のz座標と一致しないため、使用できません。 そして、一致するのはw-座標です。これは、カメラ空間から明示的にzを配置するためです（マトリックスの4列目を見てください）。 実際、 z自体でなく1 / zが必要です。 NDCに切り替えると、すべての頂点がz （w座標にある）で除算されるため、実際には「無料」で取得できます。

float const w_inversed{ 1.0f / vw }; vx *= w_inversed; vy *= w_inversed; vz *= w_inversed; // NDC to screen // ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、これを単純に反対の値に置き換えることができます。

 float const w_inversed{ 1.0f / vw }; vx *= w_inversed; vy *= w_inversed; vz *= w_inversed; vw = w_inversed; // NDC to screen // ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ラスタライズアルゴリズム

以下では、ポリゴンをラスタライズする3つのアプローチについて説明します。 コード例の多くは実装に依存しているため、完全なコード例はありません。これは、支援するよりも混乱を招くでしょう。 記事の最後にプロジェクトへのリンクがあり、必要に応じてプロジェクトの実装コードを見ることができます。

「標準」アルゴリズム

このアルゴリズムは、ソフトウェアレンダラーで最も一般的に説明されているラスタライズアルゴリズムであるため、このアルゴリズムを「標準」と呼んでいます。 トラバーサルアルゴリズムや均一な座標でのラスタライズよりも理解しやすく、したがって、実装も容易です。



それでは、ラスタライズしたい三角形から始めましょう。 まず、これが水平な底面を持つ三角形であるとします。







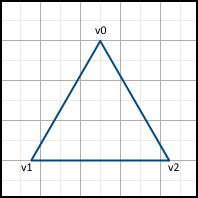
このアルゴリズムの本質は、側面に沿って順次移動し、側面間のピクセルを埋めることです。 このため、 X軸に沿った変位値は、Y軸に沿った単位ごとの変位ごとに最初に計算されます。











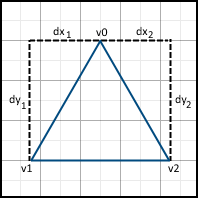
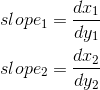
次に、側面に沿った動きが始まります。 ピクセルvはこれらの点で表されるため、移動は頂点v0の Y座標からではなく、最も近い中心から開始することが重要です。 Y座標v0が既に中心にある場合、 v0は左と右の両方の面にあるため、この軸の次の中心に移動します。つまり、このピクセルは画像に含まれません。







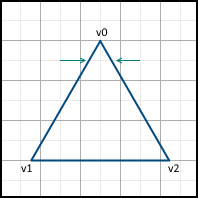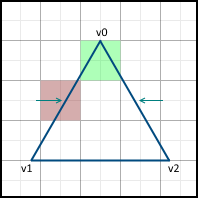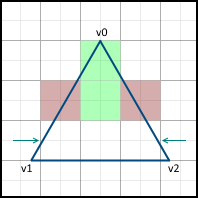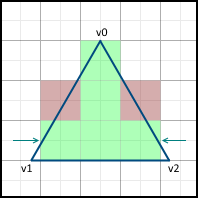
次の行に移動すると、X軸に沿って次の中心からのみ移動を開始します。顔がピクセルの中心を通過する場合、右側ではなく左側の画像にピクセルを含めます。



同様に、アルゴリズムは、上部が水平の三角形に対しても機能します。 水平辺を持たない三角形は、単純に2つの三角形に分割されます。1つは水平の上部、もう1つは水平の下部です。 これを行うために、三角形の頂点の1つ（ Y座標の平均）を通る水平線と他の面の交点を探します。







その後、これらの三角形はそれぞれ上記のアルゴリズムに従ってラスタライズされます。 また、新しい頂点でz座標とw座標の値を正しく計算する必要があります-たとえば、それらを補間します。 同様に、属性を補間するときにこの頂点の存在を考慮する必要があります。



属性は、次のように遠近補正なしで補間されます-側面に沿って移動するとき、ラスタライズするラインの開始点と終了点で補間された属性値を計算します。 次に、これらの値はこの線に沿って線形補間されます。 属性に遠近感の補正が必要な場合は、代わりにポリゴンの面に沿ってT / zを補間します（単にT-属性値のみを補間するのではなく） 1 / z 。 次に、線の始点と終点のこれらの値はそれに沿って補間され、上記の式に従って視点を考慮して最終的な属性値を取得するために使用されます。 私が言及する1 / zは、実際にすべての変換が行われた後のベクトルのw座標にあることに注意してください。

トラバーサルアルゴリズム

これは、多角形の面の方程式に基づいて同じアプローチを使用するアルゴリズムのグループ全体です。



面の方程式は、その面が存在する線の方程式です。 つまり、これはポリゴンの2つの頂点を通る直線の方程式です。 したがって、各三角形は次の3つの線形方程式で特徴付けられます。







まず、2つのポイントを通る直線の方程式について説明します（これらは三角形の頂点のペアです）。







次のように書き換えることができます。















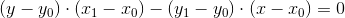
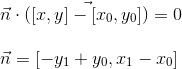
最後の式から、ベクトルnはベクトルv0-v1に垂直であることがわかります（座標は交換され、X座標はマイナス記号で取得されます）。 したがって、nは2つの頂点によって形成される線の法線です。 これはすべて線の等式であり、したがって、ポイント（x、y）をそこに代入してゼロにすると、このポイントが線上にあることがわかります。 残りの値はどうですか？ ここでは、法線のある録音フォームが役立ちます。 2つのベクトルのスカラー積が、2番目のベクトルの長さで乗算された2番目のベクトルへの最初のベクトルの投影の長さを計算することを知っています。 法線は最初のベクトルとして機能し、最初の頂点からポイント（x、y）までの2番目のベクトルとして機能します。







また、次の3つのオプションがあります。

• 値は0-ポイントは直線上にあります。
• 0より大きい値-ポイントは正の半平面にあります
• 0より小さい値-ポイントは負の半平面にあります

それらはすべて以下に示されています。











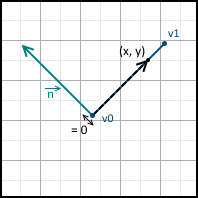
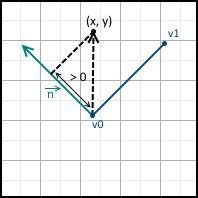
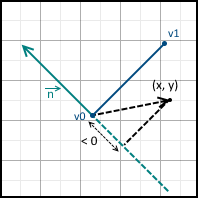
法線が反対方向を指すように線の方程式を設定することもできます-マイナス1を掛けるだけです。 将来、方程式は三角形の内側の法線が指すように設計されると仮定します。



これらの方程式を使用して、3つの正の半平面の交点として三角形を定義できます。



したがって、トラバーサルアルゴリズムの一般的な部分は次のとおりです。

• ポイントの面の方程式の値を計算します
• すべての値が正の場合、ピクセルは塗りつぶされます。 それらのいずれかがゼロの場合、ピクセルは面の1つにあり、左上ルールを使用してピクセルがポリゴンに属するかどうかを決定します
• 次のピクセルに移動

左上のルールの実装について詳しく見てみましょう。 面の法線を操作しているので、左面と上面のより厳密な定義を行うことができます。

• 左側は、法線が正のx座標を持つ（つまり、右を指す）面です。
• 上面は、Y軸が上向きの場合、法線が負のy座標を持つ面です。 Y軸が下を向いている場合（このオプションに固執します）、上面のy座標は正です

また、法線座標が線の正準方程式の係数aおよびbと一致することに注意することも重要です： ax + by + c = 0 。



以下は、ピクセルが面の1つに対して正の半平面にあるかどうかを決定する関数の例です（左上の規則を使用）。 入力に対して3つの引数をとるだけで十分です。ポイントでの顔の方程式の値と法線の座標です。

コード例

 inline bool pipeline::is_point_on_positive_halfplane_top_left( float const edge_equation_value, float const edge_equation_a, float const edge_equation_b) const { //     ,  top-left rule // if (std::abs(edge_equation_value) < EPSILON) { if (std::abs(edge_equation_a) < EPSILON) { // edge.a == 0.0f,    ,  ,   // //  y-  ,     //    return edge_equation_b > 0.0f; } else { //  x-  ,     //    return edge_equation_a > 0.0f; } } else { //  ,      return edge_equation_value > 0.0f; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

方程式の値を計算するときの単純で便利な最適化：座標（x、y）を持つピクセルの値がわかっている場合、ポイント（x + 1、y）で値を計算するには、係数aの値を追加するだけで十分です。 同様に、 （x、y + 1）の値を計算するには、係数bを追加するだけで十分です。







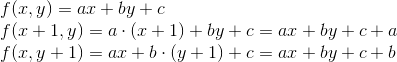
次のステップは、属性補間と遠近補正です。 このために、重心座標が使用されます。 これらは、三角形の点が頂点の線形結合として記述される座標です（正式には、その点が三角形の質量の中心であり、対応する頂点の重みがあることを意味します）。 正規化されたバージョンを使用します-つまり 3つの頂点の合計重みは1に等しくなります。











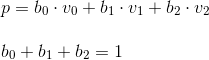
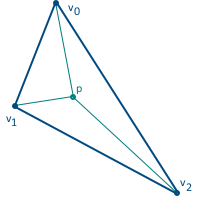
この座標系には、計算を可能にする非常に便利なプロパティもあります：重心座標は、上の図で形成された三角形の面積と三角形の総面積の比に等しい（このため、面積座標とも呼ばれます）：











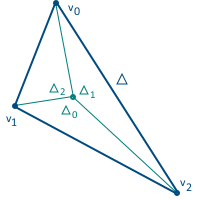
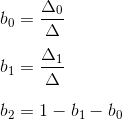
3つの座標の合計は1に等しいため、3番目の座標は三角形の面積を介さずに計算できます。実際、2つの自由度しかありません。



これで、すべてが線形属性補間の準備ができました。三角形の指定された点の属性値は、対応する頂点の重心座標と属性値の線形結合に等しくなります。







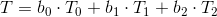
パースペクティブを修正するには、別の式を使用します。まず、補間値T / zを計算し、次に補間値1 / zを計算し、それらを互いに分割してパースペクティブを考慮したTの最終値を取得します。







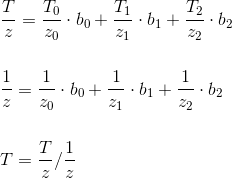
さまざまなトラバーサルアルゴリズムの違いは、検証用のピクセルの選択方法です。 いくつかのオプションを検討します。

AABBアルゴリズム

名前が示すように、このアルゴリズムは単純にポリゴンの軸に合わせた境界ボックスを構築し、ポリゴン内のすべてのピクセルを通過します。 例：

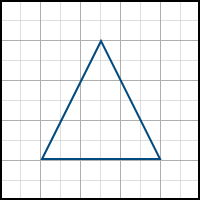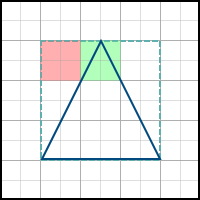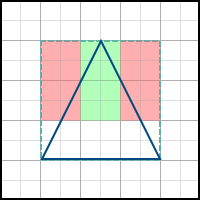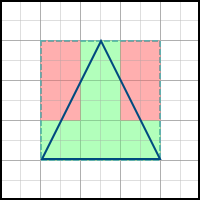
バックトラッキングアルゴリズム

このアルゴリズムは、次の手順で構成されます。

• 最上部の頂点の下の最上部のピクセルから開始します
• ポリゴンの左側のピクセルに達するまで左に移動します（バックトラッキング）
• 右に移動し、ポリゴンの右のピクセルに出会うまでピクセルをペイントします
• 下の行に移動して、2番目のステップからやり直してください。

これは次のように表すことができます。







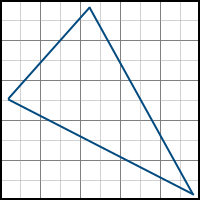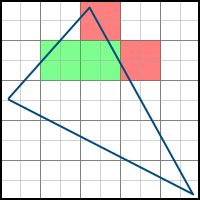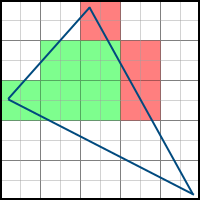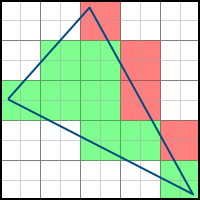
ピクセルがポリゴンの左にあることを次のように確認できます-法線が右を指す（つまりa> 0）少なくとも1つの面では、この面の方程式の値は負です。

ジグザグアルゴリズム

このアルゴリズムは、バックトラッキングアルゴリズムの改良版と見なすことができます。 右に移動できるピクセルができるまで行のピクセルを「アイドリング」する代わりに、行の移動を開始したピクセルに関する情報を覚えてから、ピクセルを左右に移動します彼。

• 最上部の頂点の下の最上部のピクセルから開始します
• 位置を覚えて
• 左に移動して、ポリゴンの左側のピクセルに出会うまで、ポリゴンに入るピクセルの上にペイントします（バックトラッキング）
• 開始したピクセルに戻り（手順2で記憶しました）、右に移動して、ポリゴンの外側のピクセルに達するまで、ポリゴンに入るピクセルを埋めます。
• 下の行に移動して、2番目のステップからやり直してください。

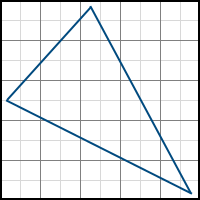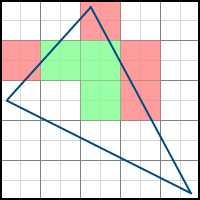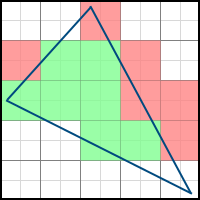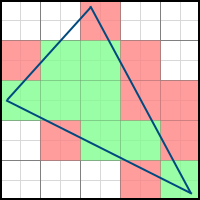
同次座標のラスタライズアルゴリズム

このアルゴリズムは元々 、2D同次座標を使用した三角形スキャン変換、Marc Olano＆Trey Greerの出版物で説明されていました。 その主な利点は、頂点の変換中にw座標によるクリッピングと除算の必要がないことです（いくつかの予約を除きます-それらについては後で説明します）。



まず、ラスタライズの開始時に、頂点のx座標とy座標に、対応するw座標で単純に除算することにより、画面上の座標にマッピングされる値が含まれていると仮定します。 これは、W座標による除算を含まないため、いくつかのラスタライズアルゴリズムがサポートされている場合、頂点変換コードをわずかに変更できます。 同種の2次元空間の座標は、ラスタライズを実行する関数に直接転送されます。



ポリゴンに沿った属性の線形補間の問題をより詳細に検討してみましょう。 属性の値（これをpと呼びましょう）は線形に増加するため、次の方程式を（3次元空間で）満たす必要があります。







点（x、y、z）は同次座標（x、y、w）を使用して平面に投影されるので（ w = z ） 、同次座標でこの方程式を書くこともできます。







係数a 、 b、およびcを知っていると想像してください（少し後で見つけることを検討します）。 ラスタライズ中、画面空間内のピクセルの座標を処理します。これは、次の式に従って均一空間内の座標に関連付けられます（これは最初の仮定でした）。







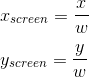
wで割ることにより、画面空間の座標のみを使用してp / wの値を表現できます。







スクリーン座標を使用して正しいp値を取得するには、この値を1 / wで除算するだけです（または、同じことで、 wで乗算します）。







同様に、 1 / wは同様のアルゴリズムで計算できます。すべての頂点で同じパラメーターp = [1 1 1]があると想像するだけで十分です。



次に、係数a 、 b、およびcを見つける方法を検討します。 各属性の値はポリゴンの頂点で設定されるため、実際には次の形式の方程式系があります。







このシステムをマトリックス形式で書き換えることができます。







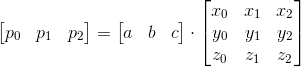
そして解決策：







ポリゴンごとに1つの逆行列のみを計算する必要があることに注意することが重要です。これらの係数を使用して、画面上の任意のポイントで正しい属性値を見つけることができます。 また、行列の行列式を逆算するために計算する必要があるため、行列式は原点に頂点を持ち、多角形の点に2を掛けた四面体の体積も計算するため、補助情報を取得します（これはベクトルの混合積の定義から得られます）。 行列式がゼロの場合、これはポリゴンが描画できないことを意味します。ポリゴンは縮退しているか、カメラに対してエッジによって回転しているためです。 また、四面体の体積にはプラス記号とマイナス記号を付けることができます。これを使用して、カメラに「戻る」ポリゴン（「背面カリング」）を切り取ることができます。 頂点を反時計回りに並べることが正しいと考える場合、行列式の値が正であるポリゴンはスキップする必要があります（左手座標系が使用されている場合）。



このように、属性補間の問題はすでに解決されています-画面上の特定のポイントで任意の属性の正しい値を計算できます（視点を考慮に入れて）。 ポリゴンが画面上のどのポイントに属するかを決定するためだけに残ります。



トラバースアルゴリズムでポリゴンへのピクセルの所属がどのように検証されたかを思い出してみましょう。 面の方程式を計算し、画面上の目的のポイントで値を確認しました。 それらがすべて正（またはゼロであるが、左面または上面に属している）である場合、ピクセル上にペイントしました。 三角形の表面に沿って属性を補間する方法をすでに知っているので、反対の頂点（実際にはこれは平面です）に沿ってゼロに等しい擬似属性と正の値（最も便利なのは1）を補間すると仮定して、まったく同じアプローチを使用できますこれらの面を通過する）：







したがって、各面のこれらの擬似属性の値：







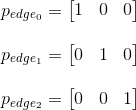
それらを使用して、各面に対応する係数a 、 b、およびcを計算し、それらの方程式を取得できます。







これで、三角形の表面に沿って同様に値を補間し、必要なポイントで値を計算できます。 正であるか、ゼロであるが、左端と上端にある場合、ピクセルはポリゴンの内側にあり、塗りつぶす必要があります。 また、小さな最適化を適用することもできます-面の方程式の正確な値はまったく必要なく、その符号だけで十分です。 したがって、 1 / wによる除算は回避でき、 p / wと1 / wの符号をチェックするだけでよく、一致する必要があります。



同じフェース方程式を操作するため、トラバーサルアルゴリズムのセクションで述べた内容の多くは、このアルゴリズムにも適用できます。 たとえば、左上のルールは同様の方法で実装でき、面の方程式の値は増分的に計算できます。これは便利な最適化です。



このアルゴリズムを導入するときに、このアルゴリズムは均一な座標で動作するため、クリッピングを必要としないと書きました。 これは、1つのケースを除き、ほぼ完全に真実です。 原点に近い（または一致する）ポイントのw座標を操作する場合があります。 この場合、属性の補間中にオーバーフローが発生する可能性があります。 そのため、このようなエラーを回避するために、 xy平面に平行で、原点に近い距離zにある別の「面」を追加することをお勧めします。



トラバーサルアルゴリズムを説明するときに、三角形をチェックするピクセルのセットを選択するためのいくつかのオプションについて言及しました（軸整列境界ボックス、バックトラッキング、ジグザグアルゴリズム）。 ここで適用できます。 これは、境界値（たとえば、バウンディングボックスの座標）を計算するために頂点をw座標で除算する必要がある状況です。w<= 0の場合のみ状況を予測する必要があります 。 もちろん、他の方法もあります。 画面のすべてのピクセルを通過することは、パフォーマンスの観点から明らかに失敗します。 また、タイルラスタ化を使用することもできますが、その説明はこの記事の範囲外です。

それだけです

実装の例を見ることができるプロジェクト： github.com/loreglean/lantern 修正などのプルリクエストを歓迎します。コードのエラーまたはPMに関する質問について書いてください。