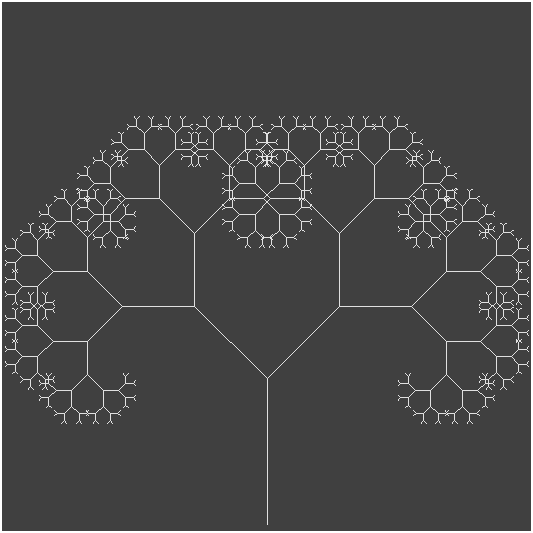
論文の研究部分で心電図のイベントを検出するためのアルゴリズムを研究すると、心電図のRR間隔の持続時間は小数点以下2桁まで計算され、特定の人の心血管系を非常に正確に特徴付けていることがわかりました。 私はかなり長い間フラクタル幾何学が好きだったので、単純なフラクタルオブジェクトに「個人的な」資質を与える方法がすぐに頭に浮かびました。
そこで、「ピタゴラスの心電図ツリー」がありました。
理論部分-1.心電図について
興奮中に心筋のさまざまな部分の間に作成された電位差のグラフィック記録は、心電図(ECG)と呼ばれます。 心電図上のこれらの心電位の向きと大きさは、歯の振幅と等電線に対する向き(極性)で表されます。 また、0.3〜3 mVの信号レベルで0.15〜300 Hzの範囲をカバーします。
通常のECGは、歯とそれらの間の水平方向の線分(セグメント)で構成されます(図1)。
図1-通常の心電図の概略図。

臨床診療では、体表のさまざまな部分からのリードが使用されます。 これらのリードは表面的と呼ばれます。 ECGを登録する際には、通常、手足から6本、胸部から6本、一般に受け入れられている12本のリードが使用されます。 最初の3つの標準リードは、Einthovenによって提案されました。 心拍数(HR)は、1心周期の持続時間によって決まります。 間隔R-Rの期間で
Einthovenによると、心拍数を決定するための標準で最も便利なのはIIリードです。 その中でR波は最大の振幅を持っています。
実用部-1
計算には、生理学的信号のデータベースから取得したEinthovenによるIIリードの健康な人の実際のECGを使用します[1]。
ECGパラメーター:
•ADCの解像度は12ビットです。
•サンプリング周波数100 Hz。
•持続時間10秒。
図2-データベースからの通常のECGの画像。
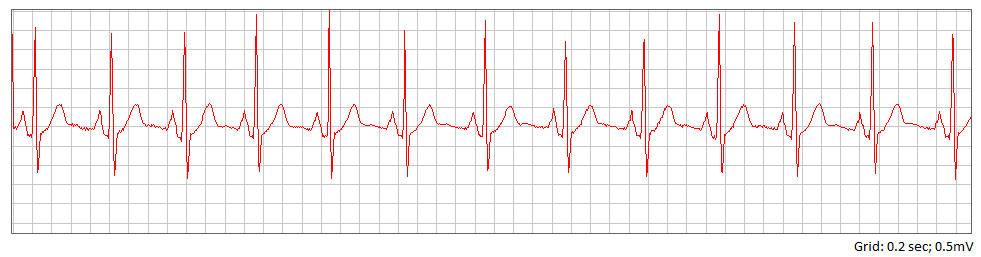
次に、R波を抽出できるようにQRS複合体を定義します。これを行うには、1次導関数の加重二乗演算子と移動平均フィルターに基づくアルゴリズムを使用します[2]。
見た目よりも難しい音:
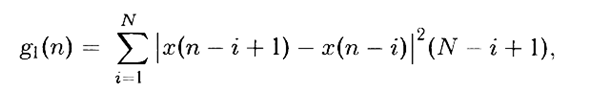
ここで、 x(n)はECG信号、 Nはウィンドウ幅です。その中で、1次差が計算され、係数(N-i + 1)を使用して2乗および重み付けされます。
重み係数は、現在の差から始まり、時間的に早いN個のサンプルによって計算された差まで直線的に減少し、平滑化効果を提供します。
さらに平滑化は、 Mポイントの移動平均フィルターを使用して実行されます。

100 Hzのサンプリング周波数では、フィルターウィンドウの幅はM = N = 8に設定されます。 このアルゴリズムは、各QRS複合体に単一のピークを与え、P波とT波を抑制します処理の結果、次のタイプのECGが得られます(図3)。
図3-ろ過後のECGの画像。

処理された信号のR波の検索は、単純なピーク検索アルゴリズムを使用して実行できます。
1.ピークが予想される信号g(n)のフラグメントをスキャンし、最大値gmaxを決定します。
2.最大値の分数としてのしきい値の定義、 Th = 0.8gmax 。
3.すべてのg(n)> Thについて、g(n)の対応する値が前または後のサンプルg(n)の特定の数Mよりも大きいサンプルが選択されます。
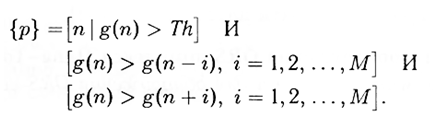
この方法で定義されたセット{p}には、信号g(n)で見つかったすべてのピークのインデックスが含まれます。
アーティファクトに起因するピークは、追加条件(たとえば、2つの隣接するピーク間の最小間隔)によって拒否される可能性があります。
図4-R歯がマークされたECGの画像。
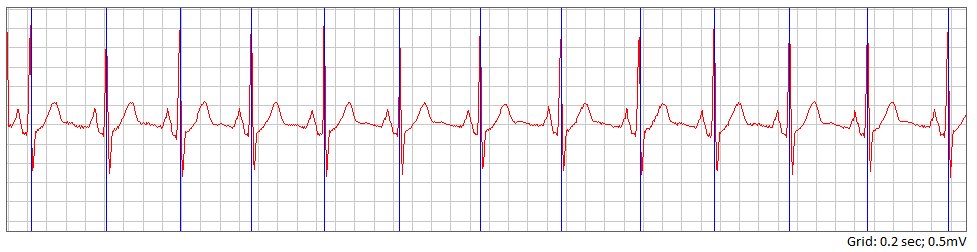
次は、単純なタスク自体です-所定のECGのRR間隔の平均長を決定します。 そして、この場合、それは733msに等しいです。 「ファン別」では、心拍数を計算します: 60 / 0.733 = 81.85拍/分。 今、特定の人の心の働きを特徴付ける価値があります。
少し説明:
心臓はメトロノームではありません;ビート間の等時間間隔でビートをタップすることはできません。 健康な人のRR間隔は小さな制限内で異なります。 間隔の変動が大きい場合-これは不整脈やその他の障害の存在を示しています。 振動メカニズムは、特定の心臓の電気伝導率に関連するプロセスの非常に複雑なセットです。
ピタゴラスの木を構築するときにパラメータとして平均RR間隔の値を使用して、「一意」(「個人」)機能を与えることができます。
理論部分-2.フラクタルについて
フラクタルは幾何学的オブジェクトと呼ばれます:線、表面、空間体、強く頑丈な形状を持ち、自己相似性の特性を持ちます。 フラクタル理論の創始者である仏米数学者ブノワマンデルブロは、ラテン分詞フラクタスからフラクタルという用語を形成しました。 対応する動詞frangereは、破壊、破壊、つまり 不規則な形状の断片を作成します。 自己相似性は、フラクタルオブジェクトの基本的な幾何学的特徴のスケール不変性(スケーリング)、スケールの変化による不変性を決定します。 フラクタルオブジェクトの破線の再現性は完全である場合があり(この場合、通常のフラクタルと呼ばれます)、ランダム性の要素が観察される場合があります(このようなフラクタルはランダムと呼ばれます)。 小さなスケールでのランダムフラクタルの構造は、オブジェクト全体とまったく同じではありませんが、統計的特性は一致しています。
ピタゴラスの木は、ピタゴラスパンツ[3]として知られる図に基づいた、幾何学的な規則的なフラクタルの一種です。
幾何学的フラクタルを構築する原理は再帰です。
実践編-2
ピタゴラスの木の構築アルゴリズム:
1)垂直セグメントを構築しています。
2)このセグメントの上端から、互いに90°の角度で短い長さの2つのセグメントを再帰的に構築します。
3)ツリーの各ブランチに対して2つの後続のセグメントを構築する関数を呼び出します。
Cでピタゴラスの木を構築する機能。
void Draw(double x, double y, double L, double a) { if(L > max) { L*=0.7; moveto(x,y); lineto((int)(x+L*cos(a)),(int)(yL*sin(a))); x=x+L*cos(a); y=yL*sin(a); Draw(x,y,L,a+Pi/n); Draw(x,y,L,a-Pi/m); } }
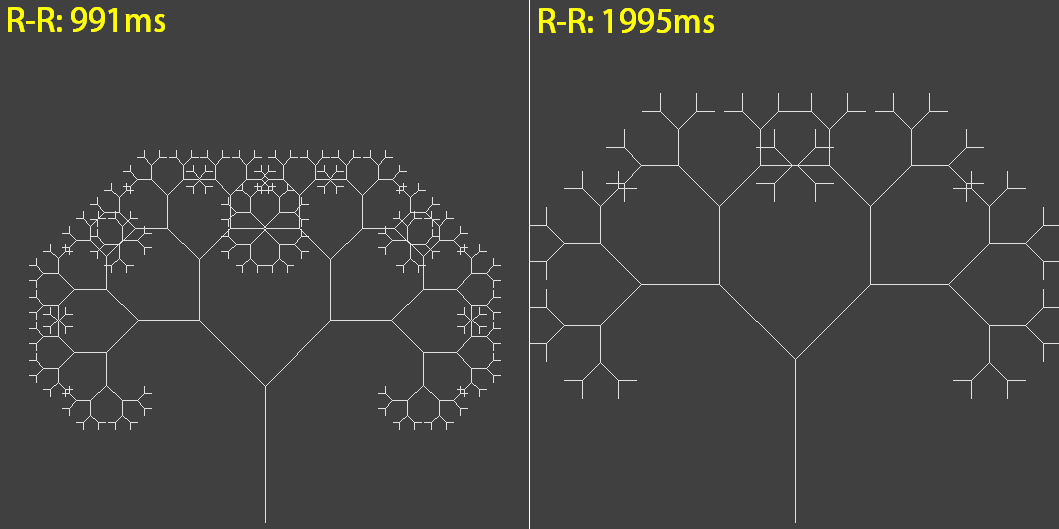
図5-RRでのECGのピタゴラスツリー:733ms。

変更する必要があるのは、計算されたECGの平均RR間隔の長さをプログラムの変数Lとして使用することだけです。
したがって、身体活動、枝の長さ、およびそのねじれに応じて「呼吸する」「個人的な」ピタゴラスの木を手に入れることができます-「あなたの性格をできるだけ正確に記述してください」。

参照資料
1.複雑な生理学的信号の研究リソース: physionet.org ;
2. Rangayyan R.M. 生物医学信号の分析。 実践的アプローチ/あたり 英語から エド。 A.P. ネミルコ。 -M。:Fizmatlit、2010 .-- 220 p。 -ISBN 978-5-9221-0730-3;
3. ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%9F%D0%B8%D1%84%D0%B0 %D0%B3%D0%BE%D1%80%D0%B0