最新のコンパイラは、コードの最適化に非常に優れています。 実行されない条件付き遷移を削除し、定数式を計算し、無意味な算術演算(1の乗算、0の加算)を取り除きます。 コンパイル時に既知のデータを操作します。
処理されたデータに関する情報の実行時には、はるかに多くなります。 それに基づいて、追加の最適化を実行し、プログラムを高速化できます。
特定のケース用に最適化されたアルゴリズムは、普遍的なアルゴリズムよりも常に高速に動作します(少なくとも遅くはありません)。
入力データの各セットに対して、このデータを処理するための最適なアルゴリズムを生成するとどうなりますか?
明らかに、実行時間の一部は最適化に費やされますが、最適化されたコードが頻繁に実行される場合、コストは利子で返済されます。
これは技術的にどのように行いますか? 非常に簡単です-必要なコードを生成するプログラムにミニコンパイラが含まれています。 このアイデアは新しいものではなく、この技術は「ランタイムコンパイル」またはJITコンパイルと呼ばれます。 JITコンパイルは、仮想マシンおよびプログラミング言語のインタープリターで重要な役割を果たします。 頻繁に使用されるコード(またはバイトコード)のセクションがマシン命令に変換されるため、パフォーマンスが大幅に向上します。
Java、Python、C#、JavaScript、Flash ActionScriptは、使用される言語の不完全な(完全に不完全な)リストです。 この技術を使用して特定の問題を解決し、何が起こるかを提案します。
挑戦する
タスクは、数式のインタープリターの実装を取得することです。 入力には次の形式の行があります
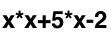
数値はxの値です。 出力は数値である必要があります-このxの値の式の値。 簡単にするために、「+」、「-」、「*」、「/」の4つの演算子のみを処理します。
この段階では、文字列はそれを表現するのに最も便利な方法ではないため、この式をどのようにコンパイルできるかはまだ明確ではありません。 分析と計算には、解析ツリー、この場合はバイナリツリーの方が適しています。
元の式の場合、次のようになります。
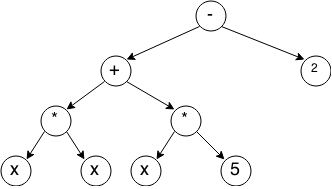
ツリーの各ノードは演算子であり、その子はオペランドです。 ツリーの葉は定数と変数です。
このようなツリーを構築するための最も簡単なアルゴリズムは、再帰降下です。各段階で、優先度が最も低い演算子を見つけ、式を2つの部分に分割します。この演算子の前と後に、これらの部分の構築操作を再帰的に呼び出します。 アルゴリズムの段階的な説明:
ここでは、単純な理由でアルゴリズムの実装を説明しません-それは非常に膨大であり、記事はそれについてではありません。
ツリーはノードで構成され、各ノードはTreeNode構造で表されます
typedef struct TreeNode TreeNode ;
struct treeNode
{
TreeNodeTypeタイプ; //ノードタイプ
TreeNode *左; //左の子にリンクします
TreeNode * right ; //正しい子のリンク
float値; //値(定数ノード用)
} ;
考えられるすべてのタイプのノードは次のとおりです。
typedef 列挙型
{
OperatorPlus 、 // Operator Plus
OperatorMinus 、 //演算子マイナス
OperatorMul 、 //演算子の乗算
OperatorDiv 、 //演算子分割
OperandConst 、 //オペランド-定数
OperandVar 、 //オペランド-変数
OperandNegVar 、 //オペランド-マイナスでとられた変数(単項マイナスの処理用)
} TreeNodeType ;
与えられたxの式の値は非常に簡単に計算されます-深さのウォークを使用して。
これも再帰を使用して実装されます。
float calcTreeFromRoot ( TreeNode * root 、 float x )
{
if ( root- > type == OperandVar )
return x ;
if ( root- > type == OperandNegVar )
return - x ;
if ( root- > type == OperandConst )
ルート->値を返します。
スイッチ ( root- > type )
{
ケース OperatorPlus :
return calcTreeFromRoot ( root- > left 、 x ) + calcTreeFromRoot ( root- > right 、 x ) ;
case OperatorMinus :
return calcTreeFromRoot (ルート->左、 x ) -calcTreeFromRoot (ルート->右、 x ) ;
ケース OperatorMul :
return calcTreeFromRoot ( root- > left 、 x ) * calcTreeFromRoot ( root- > right 、 x ) ;
ケース OperatorDiv :
return calcTreeFromRoot ( root- > left 、 x ) / calcTreeFromRoot ( root- > right 、 x ) ;
}
}
現時点では何ですか?
- 式のツリーが生成されます
- 式の値を計算する必要がある場合、再帰関数calcTreeFromRootが呼び出されます
アセンブリ段階で式を知っていた場合、コードはどのようになりますか?
float calcExpression ( float x )
{
return x * x + 5 * x - 2 ;
}
この場合、式の値の計算は、1つの非常に単純な関数の呼び出しに削減されます-再帰的なツリートラバーサルよりも何倍も高速です。
コンパイル時間!
IA32に類似したアーキテクチャのプロセッサに基づいて、x86プラットフォーム用のコードを生成することに注意してください。 さらに、フロートのサイズは4バイト、intのサイズは4バイトであると想定します。
理論
したがって、私たちのタスクは、必要に応じて呼び出すことができるC言語の通常の機能を取得することです。
まず、プロトタイプを定義しましょう。
typedef float _cdecl ( * Func ) ( float ) ;
これで、Funcデータ型は、float型の値を返す関数へのポインタになり、float型の引数を1つ受け取ります。
_cdeclは、C宣言の呼び出し規約が使用されていることを示します。
これは、Cの標準的な呼び出し規則です。
-引数は、スタックを右から左に渡されます(スタックの最上部で呼び出される場合、最初の引数は次のようになります)
-整数値はEAXレジスタを介して返されます
-浮動小数点値はレジスタst0を介して返されます
- 呼び出し関数は、レジスタeax、edx、ecxの安全性を担当します。
-残りのレジスタは、呼び出された関数によって復元する必要があります
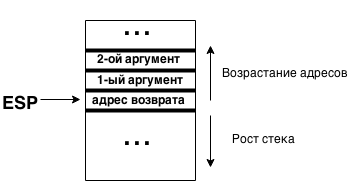
関数呼び出しは次のようになります。
push ebp //スタックフレームポインターを保存します
push arg3 //右から左の順にスタックに引数を引きます(最後の最初の引数)
arg2をプッシュ
arg1をプッシュ
call func //呼び出し自体
add esp 、 0xC //スタックへのポインタを復元します(4バイトの3つの引数は0xCバイトを占有します)
pop ebp //スタックフレームポインターを復元する
呼び出し時のスタックの状態:
式を評価するコードをどのように生成しますか? スタック計算機のようなものがあることを思い出してください。 彼はどのように働いていますか? 入力番号と演算子。 仕事のアルゴリズムは基本的です:
-定数または変数を満たしました-スタックに配置します
-演算子に適合-スタック2オペランドから削除、操作を実行、結果をスタックに配置
ただし、特定の方法でスタック計算機に入力する必要があります。これは、逆ポーランド記法で提示された式で機能します。 その特異性は、オペランドが最初にレコードにあり、次に演算子にあるという事実にあります。 したがって、元の式は次のようになります。

式に対応するスタック計算機のプログラム:
xを押す
xを押す
マル
プッシュ 5
xを押す
マル
加える
プッシュ 2
サブ
アセンブラープログラムに非常に似ていますか?
式を逆ポーランド表記に変換し、基本規則に従ってコードを作成すれば十分であることがわかります。
変換は非常に簡単です-解析ツリーがすでに構築されているので、深さを調べるだけで、頂点を出るときに対応するアクションを生成します-必要な順序でコマンドのシーケンスを取得します。
このアクションの擬似コード:
static void generateCodeR ( TreeNode * root 、 ByteArray * code )
{
if ( root- > left &amp ;&amp ; root- > right )
{
generateCodeR (ルート->右、コード) ; //最初に生成する必要があります
generateCodeR (ルート->左、コード) ; //子要素の計算コード
}
//親要素のコードを生成します
if ( root- > type == OperandVar )
{
コード+ = "プッシュx" ; //引数(変数)の値をスタックに配置します
}
else if ( root- > type == OperandNegVar )
{
コード+ = "push -x" ; //符号を変更して引数の値をスタックに配置します
}
else if ( root- > type == OperandConst )
{
code + = "push" + root- > value ; //定数をスタックに配置します
}
他に
{
コード+ = "ポップ" ; //スタックから削除
コード+ = "ポップ" ; // 2つの値
スイッチ ( root- > type )
{
ケース OperatorPlus :
コード+ = "追加" ; //追加を実行します
休憩 ;
case OperatorMinus :
コード+ = "sub" ; //減算
休憩 ;
ケース OperatorMul :
コード+ = "mul" ; //乗算を実行します
休憩 ;
ケース OperatorDiv :
コード+ = "div" ; //分割を行います
休憩 ;
}
code + = "push result" //算術演算の結果をスタックに保存します
}
}
実装
まず、スタックを決定しましょう。すべてがシンプルです-espレジスタには最上部へのポインタが含まれています。 そこに何かを置くには、コマンドを実行するだけです
プッシュ {値}
または、ESPから数値4を減算し、受信したアドレスに目的の値を書き込みます
sub esp 、 4
mov [ esp ] 、 {値}
スタックから削除するには、popコマンドまたはespに4を追加します。
以前は呼び出し規約について言及していました。 そのおかげで、関数の単一の引数がどこになるかを正確に知ることができます。 espアドレス(先頭)には戻りアドレスが含まれ、esp-4アドレスには引数の値のみが含まれます。 比較的頻繁にアクセスされるため、eaxレジスタに配置できます。
mov eax 、 [ esp - 4 ] ;
次に、浮動小数点数の操作について少し説明します。 x87 FPU命令セットを使用します。
FPUには、スタックを形成する8つのレジスタがあります。 それぞれが80ビットを保持します。 このスタックの最上部には、レジスタst0を介してアクセスします。 したがって、レジスタst1は、このスタック内のこの頂点に続く値、st2-次の値、などをst7にアドレス指定します。
FPUスタック:

値を一番上にロードするには、fldコマンドを使用します。 このコマンドのオペランドは、メモリに保存された値のみです。
fld [ esp ] // espに含まれるアドレスに格納されている値をst0にロードします
算術演算を実行するコマンドは非常に簡単です:fadd、fsub、fmul、fdiv。 引数にはさまざまな組み合わせがありますが、次のようにのみ使用します。
fadd dword ptr [ esp ]
fsub dword ptr [ esp ]
fmul dword ptr [ esp ]
fdiv dword ptr [ esp ]
これらすべての場合、[esp]からの値がロードされ、必要な操作が実行され、結果がst0に格納されます。
スタックから値を削除するのも簡単です。
fstp [ esp ] // FPUスタックの最上部から値を削除し、espのアドレスのメモリ位置に保存します
式では、単項マイナスを持つx変数が発生する可能性があることを思い出してください。 それを処理するには、記号を変更する必要があります。 FCHSコマンドはこのゲームに役立ちます-レジスタ符号st0のビットを反転します
これらの各コマンドについて、必要なオペコードを生成する関数によって決定します。
void genPUSH_imm32 ( ByteArray * code 、 int32_t * pValue ) ;
void genADD_ESP_4 ( ByteArray * code ) ;
void genMOV_EAX_PTR_ESP_4 ( ByteArray * code ) ;
void genFSTP ( ByteArray * code 、 void * dstAddress ) ;
void genFLD_DWORD_PTR_ESP ( ByteArray * code ) ;
void genFADD_DWORD_PTR_ESP ( ByteArray * code ) ;
void genFSUB_DWORD_PTR_ESP ( ByteArray * code ) ;
void genFMUL_DWORD_PTR_ESP ( ByteArray * code ) ;
void genFCHS ( ByteArray * code ) ;
計算機コードが正常に機能し、値を返すためには、その前後に適切な指示を追加する必要があります。 全体はgenerateCodeラッパー関数によってまとめられます:
void generateCode ( Tree * tree 、 ByteArray * resultCode )
{
ByteArray * code = resultCode ;
genMOV_EAX_ESP_4 (コード) ; //引数の値をeaxに入れます
generateCodeR (ツリー->ルート、コード) ; //計算機コードを生成します
genFLD_DWORD_PTR_ESP (コード) ;
genADD_ESP_4 (コード) ; //スタックから余分なダブルワードを削除します
genRET (コード) ; //関数を終了します
}
式の値を計算するコード生成関数の最終形式:
void generateCodeR ( TreeNode * root 、 ByteArray * resultCode )
{
ByteArray * code = resultCode ;
if ( root- > left &amp ;&amp ; root- > right )
{
generateCodeR (ルート->右、コード) ;
generateCodeR (ルート->左、コード) ;
}
if ( root- > type == OperandVar )
{
genPUSH_EAX (コード) ; //関数の引数はeaxにあります
}
else if ( root- > type == OperandNegVar )
{
genPUSH_EAX (コード) ; //スタックにロードします
genFLD_DWORD_PTR_ESP (コード) ; //変更
genFCHS (コード) ; //サイン
genFSTP_DWORD_PTR_ESP (コード) ; //スタックに戻る
}
else if ( root- > type == OperandConst )
{
genPUSH_imm32 ( code 、 ( int32_t * ) &amp ; root- > value ) ;
}
他に
{
genFLD_DWORD_PTR_ESP (コード) ; //左のオペランドをFPUにロードします..
genADD_ESP_4 (コード) ; // ...そしてスタックから削除します
スイッチ ( root- > type )
{
ケース OperatorPlus :
genFADD_DWORD_PTR_ESP (コード) ; //加算を実行します(結果はst0に保存されます)
休憩 ;
case OperatorMinus :
genFSUB_DWORD_PTR_ESP (コード) ; //減算(結果はst0に保存されます)
休憩 ;
ケース OperatorMul :
genFMUL_DWORD_PTR_ESP (コード) ; //乗算を実行します(結果はst0に保存されます)
休憩 ;
ケース OperatorDiv :
genFDIV_DWORD_PTR_ESP (コード) ; //除算を行います(結果はst0に保存されます)
休憩 ;
}
genFSTP_DWORD_PTR_ESP (コード) ; //結果をスタックに保存します(st0-> [esp])
}
}
コードを保存するためのバッファといえば。 これらの目的のために、ByteArrayコンテナータイプを作成しました。
typedef 構造体
{
intサイズ; //割り当てられたメモリのサイズ
int dataSize ; //保存されたデータの実際のサイズ
char * data ; //データへのポインター
} ByteArray ;
ByteArray * byteArrayCreate ( int initialSize ) ;
void byteArrayFree ( ByteArray * array ) ;
void byteArrayAppendData ( ByteArray * array 、 const char * data 、 int dataSize ) ;
データを最後に追加することができ、メモリの割り当てについて考える必要はありません-動的配列の一種です。
generateCode()を使用してコードを生成し、それに制御を渡すと、ほとんどの場合、プログラムがクラッシュします。 理由は単純です-実行する権限がありません。 私はWindowsで書いているので、WinAPI VirtualProtect関数はここで役立ちます。これにより、メモリ領域(またはメモリページ)のアクセス許可を設定できます。
MSDでは、次のように記述されます。
BOOL WINAPI VirtualProtect (
_In_ LPVOID lpAddress 、 //メモリ内の領域の先頭のアドレス
_In_ SIZE_T dwSize 、 //メモリ内の領域のサイズ
_In_ DWORD flNewProtect 、 //リージョン内のページの新しいアクセス設定
_Out_ PDWORD lpflOldProtect //古いアクセスパラメータを保存する変数へのポインタ
) ;
メインコンパイラ関数で使用されます。
CompiledFunc compileTree (ツリー*ツリー)
{
CompiledFunc結果;
DWORD oldP ;
ByteArray *コード;
code = byteArrayCreate ( 2 ) ; //コンテナの初期サイズは2バイトです
generateCode (ツリー、コード) ; //コードを生成します
VirtualProtect (コード->データ、コード-> dataSize 、 PAGE_EXECUTE_READWRITE 、 および oldP ) ; //実行権を付与します
結果。 code = code ;
結果。 run = ( Func )結果。 コード ->データ;
結果を返す ;
}
CompiledFunc-コードと関数へのポインターを便利に保存するための構造:
typedef 構造体
{
ByteArray *コード; //コード付きコンテナ
Func run ; //関数ポインタ
} CompiledFunc ;
コンパイラは書かれており、その使用は非常に簡単です。
ツリー*ツリー;
CompiledFunc f ;
フロート結果;
tree = buildTreeForExpression ( "x + 5" ) ;
f = compileTree (ツリー) ;
結果= f。 実行 ( 5 ) ; //結果= 10
速度のテストを実施するだけです。
テスト中
テスト中に、コンパイルされたコードのランタイムと、再帰的なツリーベースの計算アルゴリズムを比較します。 標準ライブラリのclock()関数を使用して時間を測定します。 コードセクションの作業時間を計算するには、プロファイルされた部分の前後に呼び出しの結果を保存するだけで十分です。 これらの値の差を定数CLOCKS_PER_SECで除算すると、コードランタイムを数秒で取得できます。 もちろん、これは非常に正確な測定方法ではありませんが、より正確にする必要はありませんでした。
エラーの強い影響を避けるために、関数の繰り返し呼び出しの時間を測定します。
テスト用のコード:
double measureTimeJIT ( Tree * tree 、 整数 )
{
int i ;
二重結果;
clock_t start 、 end ;
CompiledFunc f ;
start = clock ( ) ;
f = compileTree (ツリー) ;
for ( i = 0 ; i & lt ; iters ; i ++ )
{
f。 run ( ( float ) ( i % 1000 ) )) ;
}
end = clock ( ) ;
result = ( end - start ) / ( double ) CLOCKS_PER_SEC ;
compileFuncFree ( f ) ;
結果を返す ;
}
double measureTimeNormal ( Tree * tree 、 整数 )
{
int i ;
clock_t start 、 end ;
二重結果;
start = clock ( ) ;
for ( i = 0 ; i & lt ; iters ; i ++ )
{
calcTree ( tree 、 ( float ) ( i % 1000 ) ) ;
}
end = clock ( ) ;
result = ( end - start ) / ( double ) CLOCKS_PER_SEC ;
結果を返す ;
}
テスター自体のコードは、リポジトリで表示できます。 彼は、調整可能な制限内で入力データのサイズを連続的に増やし、上記のテスト関数を呼び出し、結果をファイルに書き込むだけです。
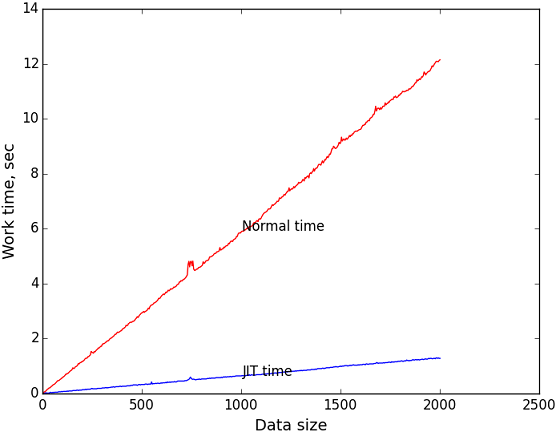
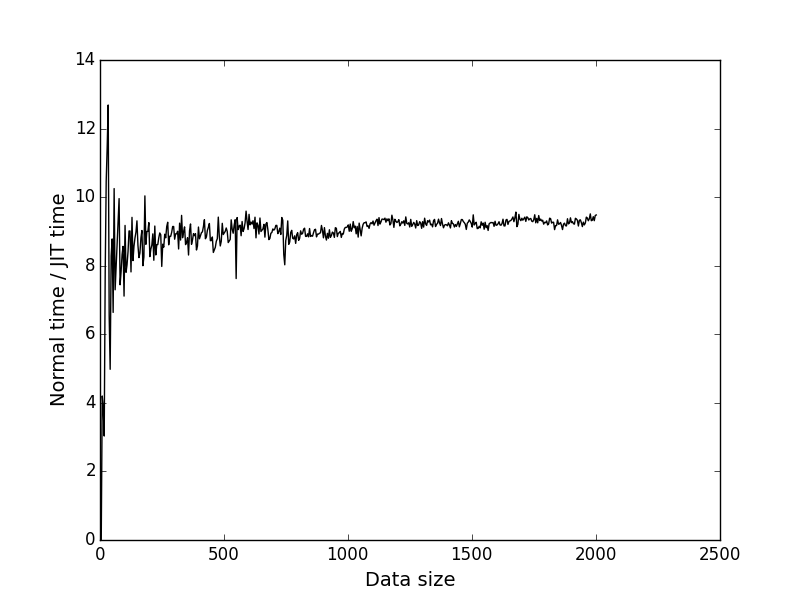
これらのデータに基づいて、入力データのサイズ(式の長さ)に対してランタイムをプロットしました。 測定の反復回数として100万を採用しました。 そのように。 ストリングの長さは、0から2000まで順次増加しました。
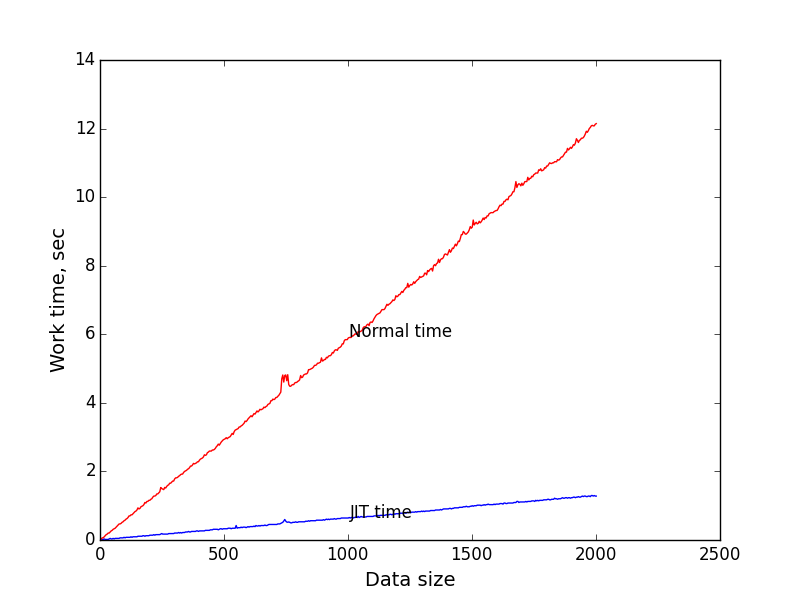
青いグラフは、コンパイルされたコードの実行時間のタスクのサイズへの依存性です。
赤いグラフは、タスクのサイズに対する再帰アルゴリズムの実行時間の依存性です。
黒いグラフは、1番目と2番目のグラフの対応するポイントのy座標です。 タスクのサイズに応じてJITが高速化される回数を示します。
入力データサイズ= 2000の場合、JITが約9.4倍勝つことがわかります。 これはかなり良いと思います。
JITの方が速いのはなぜですか?
コンパイルされたコードは完全に線形であり、単一の条件付きジャンプではありません。 このため、実行中にプロセッサパイプラインの単一のリセットが発生することはありません。これはパフォーマンスにとって非常に有益です。
より良い方法はありますか?
コンパイラの最大の問題は、FPUのすべての機能を使用しないことです。 FPU 8レジスタでは、強制的に2つ使用します。 スタックの一部をFPUスタックに転送できた場合、計算速度が大幅に向上するはずです(さらに、これはテストする必要があります)。
別の欠点は、コンパイラが非常に愚かであることです。 彼は定数式を計算せず、不必要な計算を避けません。 最大限のリソースを消費するように式を作成するのは非常に簡単です。 式の基本的な単純化を追加すると、コンパイラは理想に近づきます。
実装自体の問題は、別のプラットフォーム(コード生成機能で特定のコマンドが使用される)およびオペレーティングシステム(それでもVirtualProtect)への単純な移植の不可能性と考えることができます。 完全に明白でかなり単純なソリューションは、プラットフォーム固有の部分とOS固有の部分を抽象化し、それらの実装を個別のモジュールに配置することです。
読んでくれてありがとう、コメントとヒントを本当に楽しみにしています。
リポジトリ: bitbucket.org/Informhunter/jithabr
この記事は、「Perfect Code」という本、つまり「画像処理のためのコードの動的生成」という章に触発されました。