マイケルトロットの投稿「翻訳式...すべてのために— Piからピンクパンサー、アイザックニュートンirまで 」の翻訳。
Sylvia Torosyanの翻訳にご協力いただきありがとうございます。
この記事で使用されているすべてのコードを含むMathematicaドキュメントの形式で翻訳をダウンロードしてください （アーカイブ、約7 MB）。
Wolfram ResearchとWolfram | Alphaでは、数学とコンピューティングが大好きです。 私たちのお気に入りのトピックは、式と方程式から生じるアルゴリズムです。 たとえば、 Mathematicaは数百万の積分（より正確には、実際に遭遇する無限数）を計算でき、Wolfram | Alphaは数十万の数式を知っています（ オイラーの式とPiのBBP 式からsin（x）を含む複素定積分まで） （から例えば、式物理複数のポアズイユの法則に矩形で古典力学ソリューションスポット粒子又は超球面座標における4次元における逆距離容量 、ならびに式Dとしてあまりよく知られている式） 私は濡れた揺れ犬レート 、 砂の城の最大の高さ 、または七面鳥の調理時間を 。
最近、さまざまな形状やオブジェクトの数式を追加しました。 Wolfram | Alphaブログは、数学の方程式と不等式を使用して定義された形状形成の例を示しました。 作成された曲線の中には、 架空の人物の画像の曲線があります：
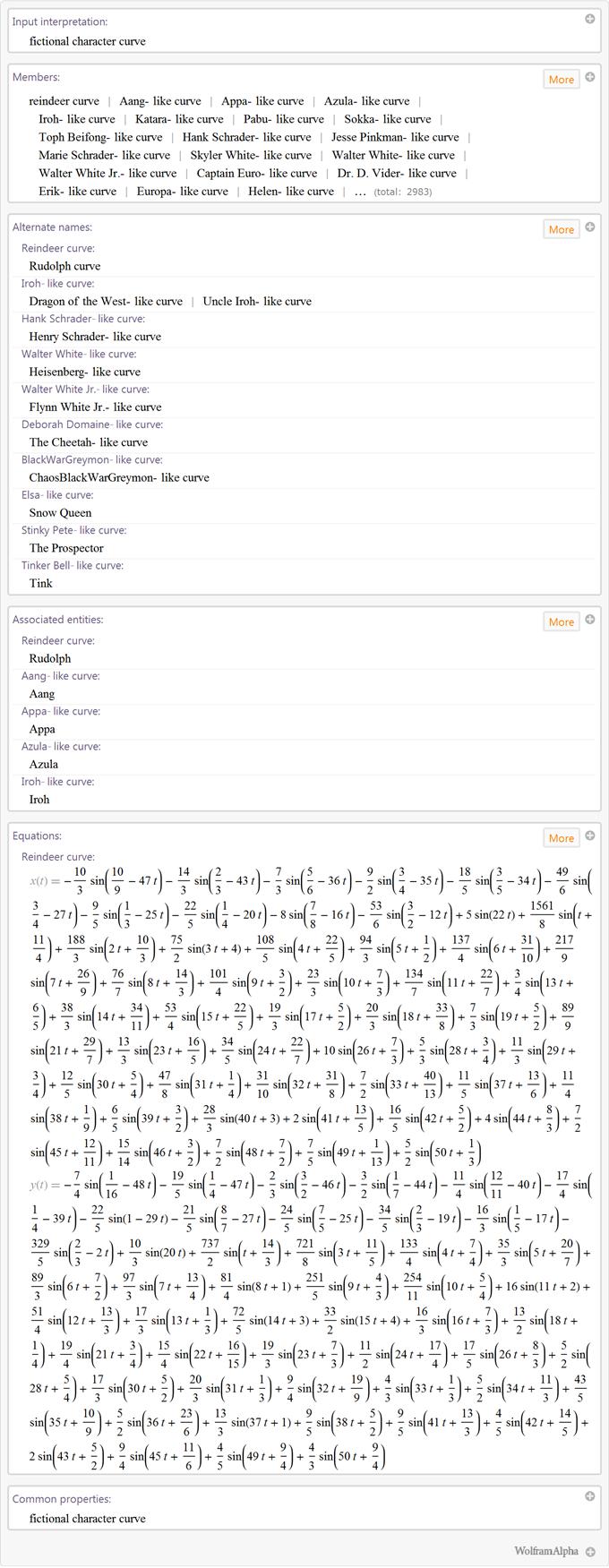
オブジェクトの輪郭の曲線 ：
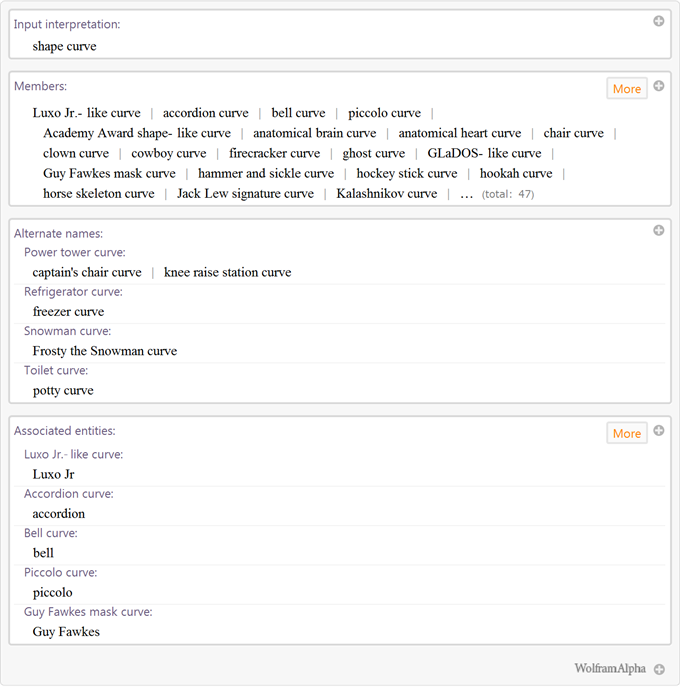
そして、私たちのユーザーの間で最も人気のある、実際の人々のイメージ曲線 ：
これらの曲線は、数学的な意味で、 レムニスケートまたはデカルトシートに似ているため、数学的な特性よりもグラフィック表現の観点からより興味深いものです。
リチャードのブログの記事が公開された後、同僚から「スティーブン・ウルフラムの顔を表す方程式をどのように作成しますか？」と尋ねられました。この質問について少し考えた後、私はそれが本当にすごいことに気づきました。式：デジタル画像（簡単にするために白黒であると想定）は、グレー値の長方形の配列です。 このような配列を使用して、補間関数、さらには多項式を構築できます。 しかし、そのような明示的な関数は非常に巨大で、数百ページの長さがあり、実際のアプリケーションには適していません。 実際、難しいのは、人の顔に似た分析表現を取得して、1ページに収まり、構造が単純になるようにすることです。 スティーブン・ウルフラムの顔を表す曲線の分析表現は約1ページの長さで、立方体の重力ポテンシャルなどの複雑な物理公式のサイズに匹敵します。
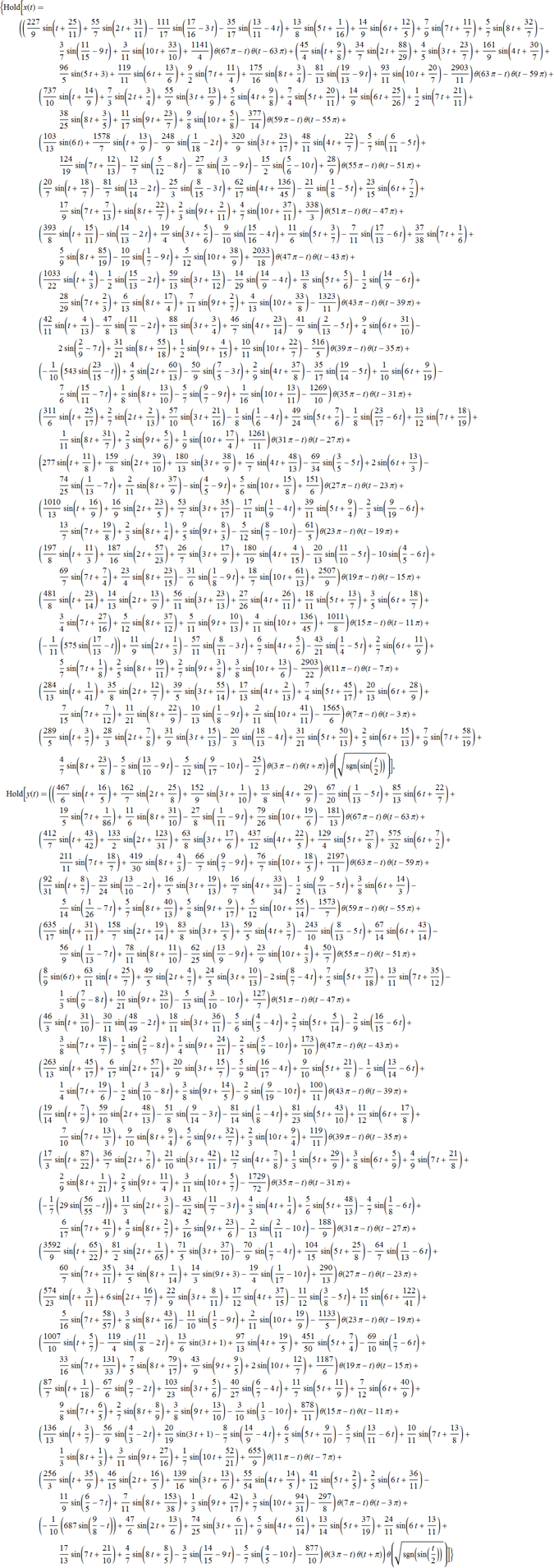
この記事では、この種の方程式を生成する方法を示したいと思います。 「計算の実行方法...」という記事で大量のMathematicaコードが表示されることは驚くことではありませんが、簡単な入門説明から始めます。
紙の上に鉛筆で絵の線を描き、線だけを描くと仮定します。 シェーディングや塗りつぶしはありません。 次に、曲線の複数のセグメントで図が作成されます。 フーリエ級数などの数学的概念により、これらの線形セグメントのそれぞれについて有限の数式を書き留めることができます。
簡単な例として、いくつかの機能を考えてみましょう
、
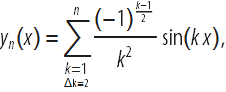
これは、さまざまな周波数と振幅の正弦波の合計です。 この関数シーケンスの最初のいくつかのメンバーは次のとおりです。
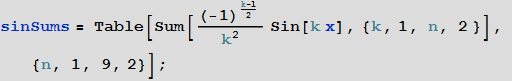
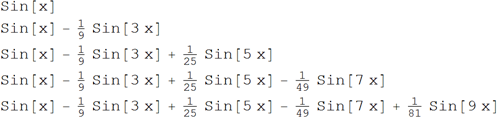
この関数シーケンスのグラフィカルな構造は、 nが増加するにつれて、関数が
三角関数になる傾向があります。
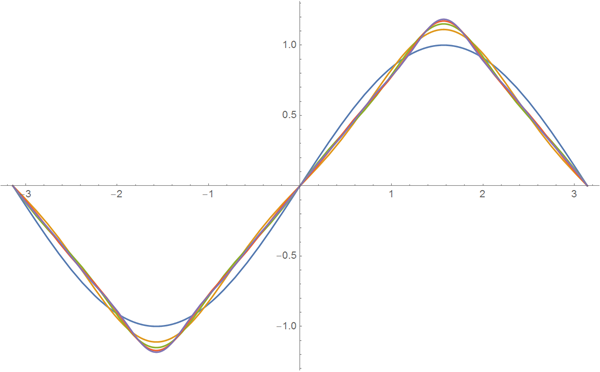
正弦関数は奇数関数であり、その結果、sin （ kx ）形式の関数の合計も奇数関数です。 コサイン関数を使用する場合、代わりに偶数の関数を取得します。 サインとコサインの値の構成により、より一般的な曲線の形を近似することができます。
上記を要約すると、問題の系列の乗算を
、また、それぞれサインとコサインから2つの行を設定します。
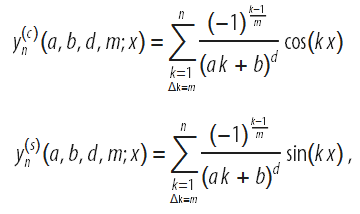
これらの関数を使用すると、より広範なクラスの関数を近似できます。
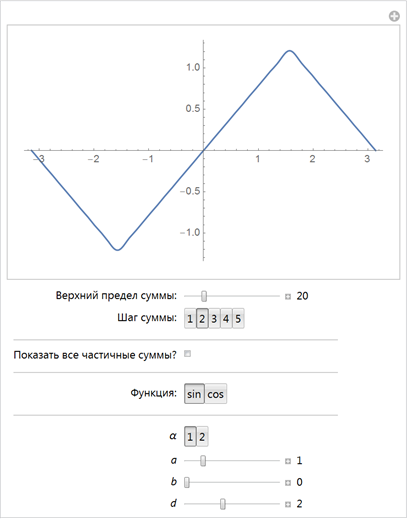
滑らかな曲線y （ x ）は、任意の区間で任意にうまく近似できることが示されます。
フーリエ級数を使用します。 さらに、滑らかな曲線の場合、係数sin（kx）およびcos（kx）の値は、 kの値が大きいとゼロになる傾向があります。
さて、パラメトリック曲線を考えます
、水平方向に独立した正弦と余弦の関数のこのような重ね合わせを使用できます 
そして垂直 
コンポーネント。
各コンポーネントで3つのサインと3つのコサインの合計を使用すると、円や楕円など、さまざまな形状がすでにカバーされています。
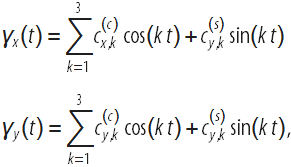
次のインタラクティブなデモでは、可能なフォームのスペースを探索できます。 2Dスライダーは、コサインおよびサイン関数の前の対応する係数を変更します。
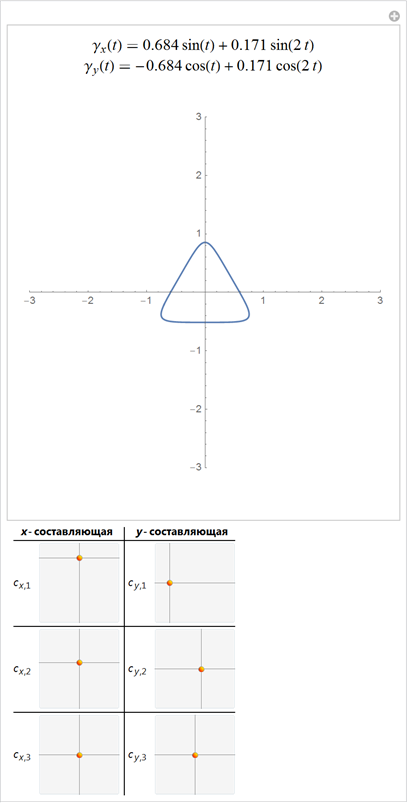
曲線のフーリエ級数の展開をカットした場合、たとえば系列の最初のn個のメンバーで、 4 n個の自由パラメーターが得られます。 考えられるすべての曲線の空間では、ほとんどの曲線はおもしろくないように見えますが、係数の一部の値では、分解は見慣れた形状を見ることができる図のように見えます。 ただし、分解係数のわずかな変更でさえ、図を大きく変更します。 次のインタラクティブな例では、曲線のフーリエ級数の最初の4×16 = 64係数を変更できます。 フーリエ級数の係数の特別なセットを使用して、さまざまな認識可能な数字を取得できます。
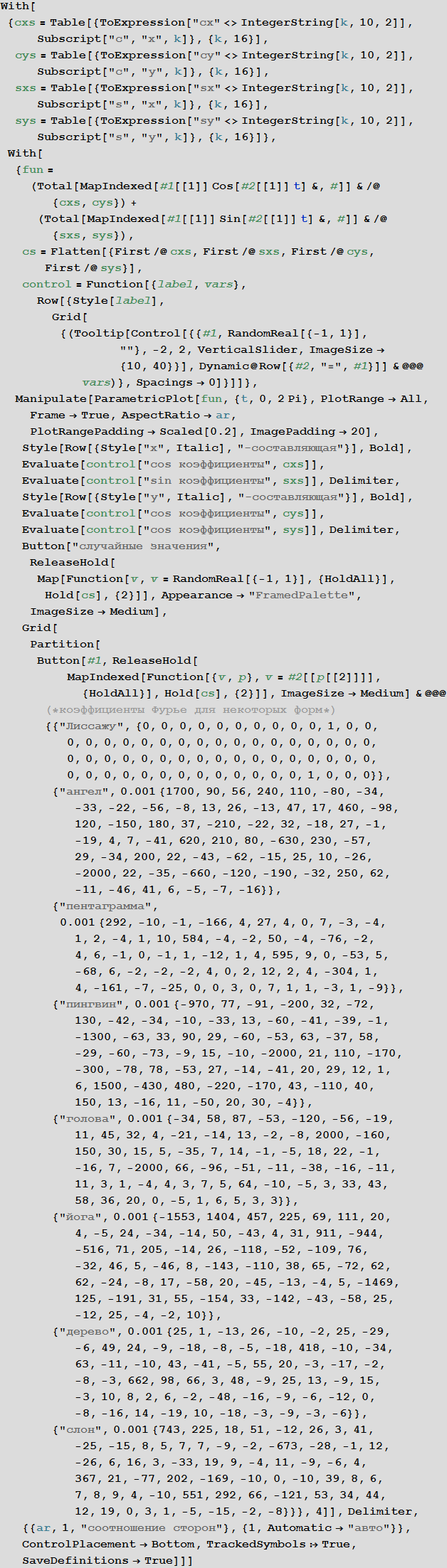
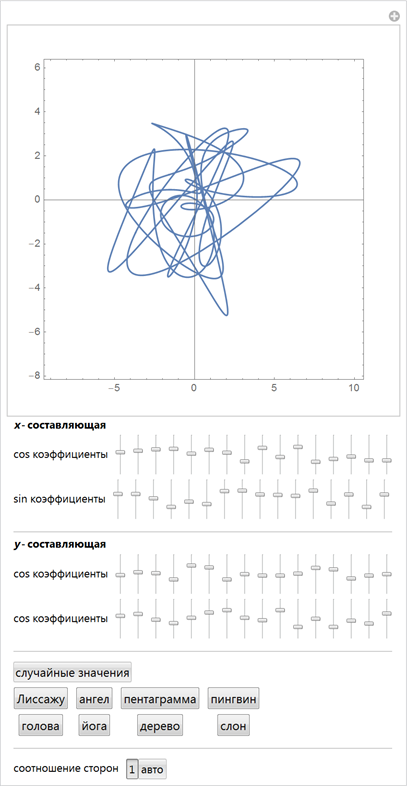
ここで複数の曲線を使用すると、顔のような画像を作成するために必要なすべてのコンポーネントが得られます。 次のインタラクティブデモでは、2つの目、2つの生徒、鼻と口を使用します。
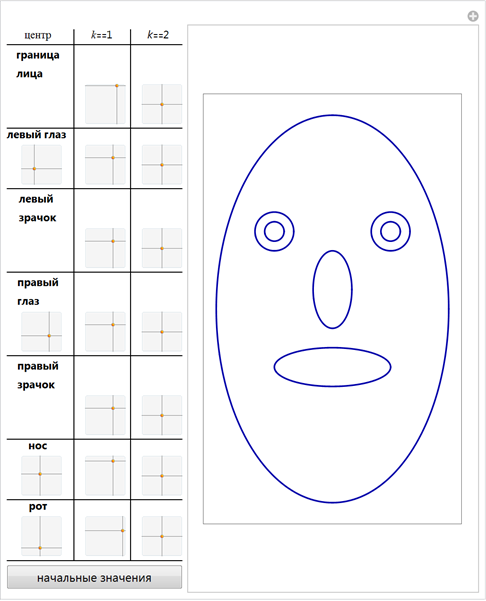
反対のことをしましょう：一連の点（青い十字）を配置して、変更可能な線を形成し、フーリエ級数で与えられた曲線に近似する曲線を作成します。
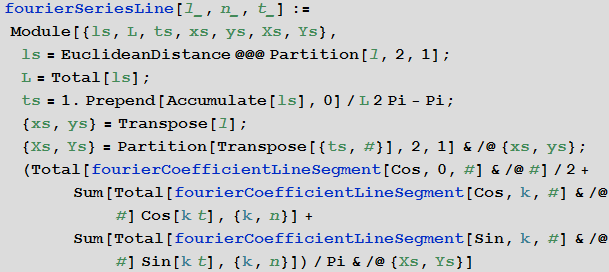
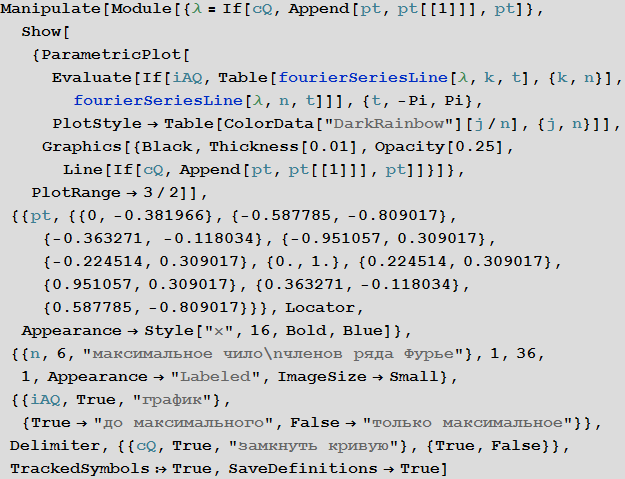
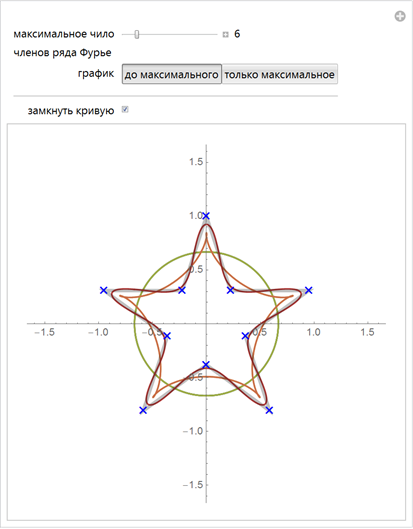
注：近似曲線を定義する方法は、フーリエ級数だけではありません。 ウェーブレットまたはスプラインを使用したり、曲線をセグメントごとに区分的にエンコードしたりできます。 または、十分な忍耐で、 リーマンゼータ関数の 普遍性の助けを借りて、 クリティカルストリップ内に任意の図形を見つけることができました 。 （驚いたことに、トーストのイエスのような可能な（かなり滑らかな）画像は、ストリップ0≤Re（s）≤1 のリーマンゼータ関数ζ （ s ）のいくつかの値に対して存在しますが、彼を見つけてください。）
これらの数値を近似するフーリエ級数に基づいた簡単な公式を見つける方法を示すために、例から始めます。正確で明確に定義された境界を持つ数値は、短い公式です。 より具体的には、よく知られている公式であるピタゴラスの定理を使用します。
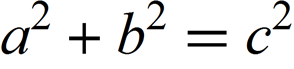
方程式をラスタライズすると、元の画像が得られます。これを使用します。
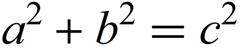
EdgeDetect関数を使用して、文字のエッジを記述するすべてのポイントのセットを簡単に取得できます。
エッジを定義するポイントができたので、それらを直線（または曲線）セグメントで接続できます。 次のpointListToLines関数は、この操作を実行します。 ランダムに選択されたポイントから開始し、それに最も近いポイントをすべて見つけます（高速な最近傍関数を使用）。 十分に近いポイントがすべて見つかるまで、このプロセスを続けます。 また、180度回転しないようにします。 曲線がどのように形成されるかを観察するには、 モニター機能を使用します。
ピタゴラスの定理の記録の画像では、境界点から11個の特定の曲線が得られます。
点のセットを組み合わせて、結果の曲線に色を付けると、文字の外側の境界線、文字aとbの内側の境界線、3つの正方形、プラス記号と等号の予想される曲線のセットが表示されます。
次に、曲線の各セグメントに対して、セグメントを近似するフーリエ級数（xおよびy成分）を見つける必要があります。 関数f（x）のフーリエ級数の通常の定義に導かれると、級数の係数は関数f（x）×cos（kx）およびsin（kx）の積分であることがわかります。 しかし今のところ、機能ではなく多くのポイントがあります。 それらを統合可能な関数に変換するために、各セグメントの曲線のBラインを作成します。 曲線のBスプラインのパラメータ化された変数は、積分変数になります。 （ポイント間の区分的線形補間の代わりにB-スプラインを使用すると、強く壊れた曲線を近似するときに追加の利点が得られます。）
数値積分を使用してフーリエ係数を取得するために必要な積分を見つけることができますが、より高速な方法は、高速フーリエ変換（ FFT ）を使用してフーリエ係数を取得することです。
より均質な曲線を取得するには、もう1つの手順を実行します。新しいパラメーター（円弧の長さ）を使用して、曲線セグメントのセットで構成される補間スプライン曲線を再パラメーター化します。 fourierComponents関数は、曲線のBスプラインの作成、円弧長のパラメーター化の繰り返しを実装し、FTTを計算してフーリエ係数を取得します。 また、 ギブス現象を回避するために曲線セグメントが開いているか閉じているかを検討します。 （上記の五角形の近似のデモンストレーションは、「曲線を閉じる」チェックボックスがオフの場合、ギブス現象をよく示しています。）
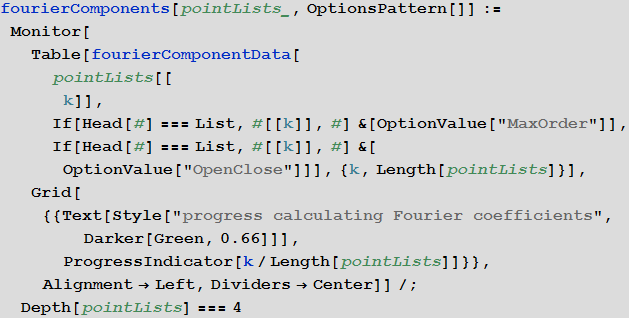
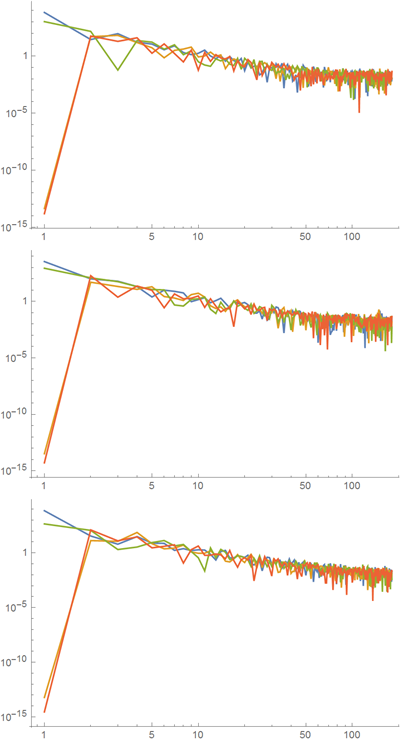
連続関数の場合、減少率の平均値を期待します
フーリエ級数のk番目の係数。 この効果は、当社が計算したフーリエ級数の係数に対しても保持される必要があります。 つまり、平均して、10番目のフーリエ係数は、最初のフーリエ係数と比較して絶対値の1％しか占めません。 これにより、大きすぎる式を取得したくないため、フーリエ級数をそれほど高次ではなくトリミングすることができます。 以下の式は、上記の曲線のフーリエ成分の平均減少率を計算します 
。 （2をわずかに下回る値は、Bスプライン曲線の点の離散化によるものです。）
以下は、最初の3つの曲線のフーリエ級数の係数の絶対値を使用した、両方の軸に沿った対数目盛のグラフです。 同時に、たとえばフーリエ係数の2次減衰に関する一般的な傾向は、隣接する係数の値が、全体として係数の減少の平均値よりも大きく変動することを示しています。
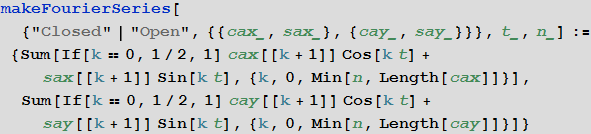
フーリエ係数にcos（kt）とsin（kt）を乗算し、これらの式を合計すると、曲線の望ましいパラメーター化が得られます。
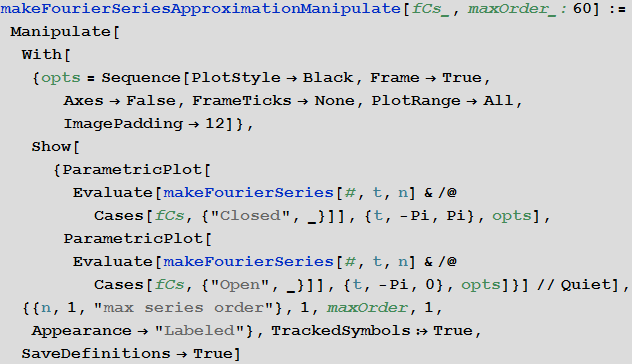
makeFourierSeriesApproximationManipulate関数は、シリーズのメンバーの数に応じて、曲線の近似を視覚化します。
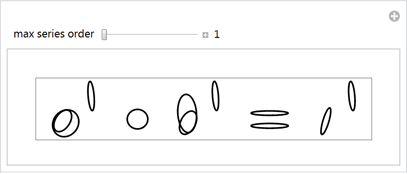
12個の楕円から始まるピタゴラスの定理に対応する図の場合、元の画像をすばやく形成し、フーリエ級数のメンバーの数を増やします。
この式が曲線の交差しないセグメントで構成される場合でも、方程式全体に対して分析式を定義します。 これを達成するために、 2πの周期を持つフーリエ級数のメンバーの周期性を使用して、対応するセグメント上の各セグメントを描画します。[0.2π]、[4π、6π]、[8π、10π]、 ...、および間隔（2π、4π）、（6π、8π）、...では、純粋に虚数の曲線の座標が得られます。 これらのセグメントでは、曲線を描くことができません。つまり、曲線の交差しないセグメントのセットを取得できます。 この構造は、2つの円のセットについて以下に示されています。
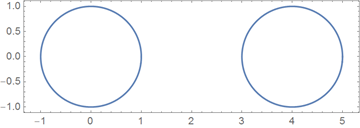
以下のグラフは、上記で構築された複素数値パラメーター化の実部と虚部を別々に示しています。 赤い線は、区間[2π、4π]からの純粋に虚数のパラメーター値を示しています。
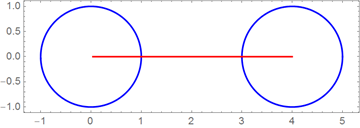
曲線の最終的な式をできる限り短くシンプルにしたいので、 sinAmplitudeForm関数を使用して、式の合計をa cos（kt）+ b sin（kt）をA sin（k t +φ）に置き換えます。フーリエ級数の近似係数を最も近い有理数に丸めます。 Piecewiseの代わりに、最終式でUnitStep関数を使用して、曲線の異なるセグメントを分離します。 実際のセグメントを明示的にリストし、描画してはならないすべてのセグメントを式で指定します
。
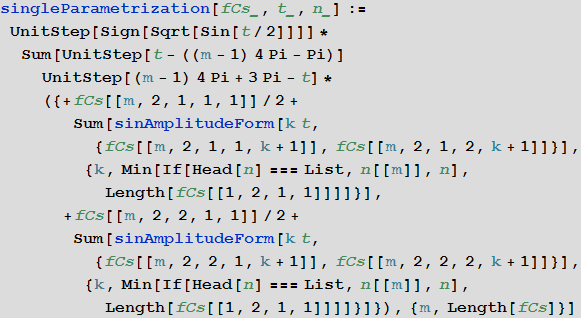
これで、ピタゴラスの定理を定義する等式を示す、写真の最終的なパラメーター化{x（t）、y（t）}を書くためのすべてができました。
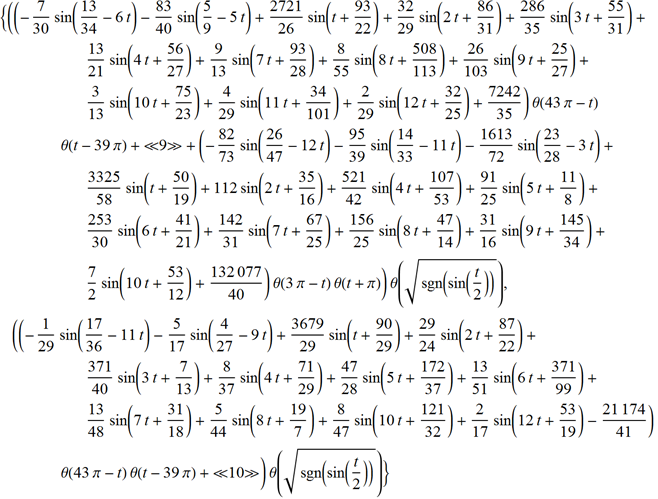
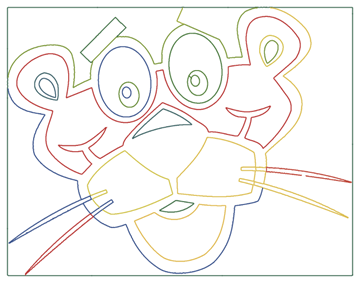
パラメータ化の基本的な考え方を説明した後、おもしろい例、 Pink Pantherを見てみましょう。 Bing検索エンジンで画像検索結果を調べると、「 閉じた形式 」の形式でパラメーター化に適した画像がすぐに見つかります。
次の画像を使用してみましょう。
パンサーの顔のすべての境界を見つけるために、 EdgeDetect関数を使用します。
曲線のエッジを接続すると、約20のセグメントが得られます。 （オプションの2番目と3番目の引数をpointListToLinesに変更することにより、より少ないまたはより多いセグメントを取得します。）
. , ; pointListToLines . .
, , .
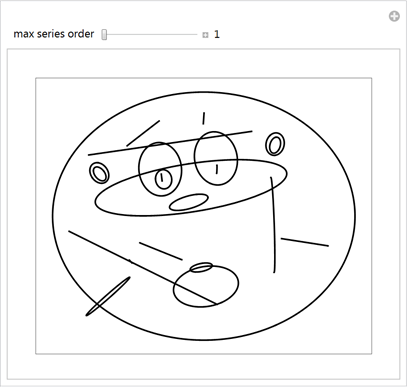
, , 20 , , .
, , .
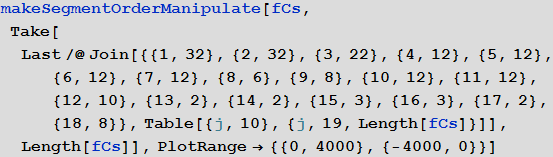
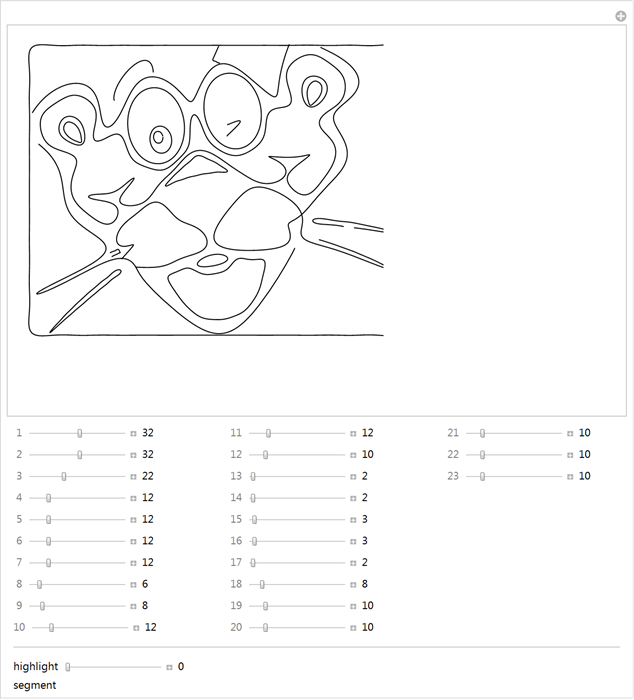
. makeSilhouetteFourierResult . : 1) ; 2) , . .
. 4 : ; -; , .
. . , . , , . ( . .) , :
, , , .
, .
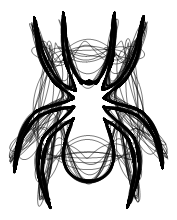
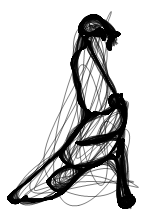
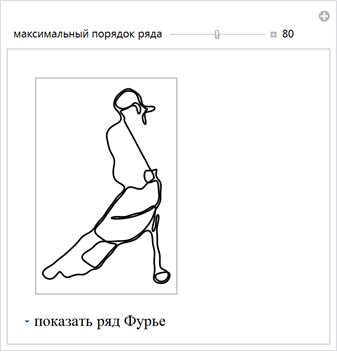
, 16 . .
, :
. , , . , .
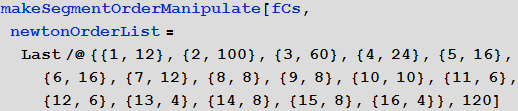
50 :
, , :
:
これで、人間の顔、架空の人物、動物、またはその他の形に似た曲線を作成する方法についての今日の議論は終わりです。次回は、上記の式から生じる無限のグラフィカルな可能性と、さまざまな画像にこの種の方程式を使用する方法について説明します。