Bresenhamのアルゴリズムは、コンピューターグラフィックスで最も古いアルゴリズムの1つです。 家庭用はんだ付け炉を作成するときに、ラスタラインを構築するアルゴリズムをどのように適用できますか？ あなたができることがわかり、非常にまともな結果が得られました。 将来的には、このアルゴリズムは低電力の8ビットマイクロコントローラーによって非常にうまく機能すると言います。 しかし、まず最初に。
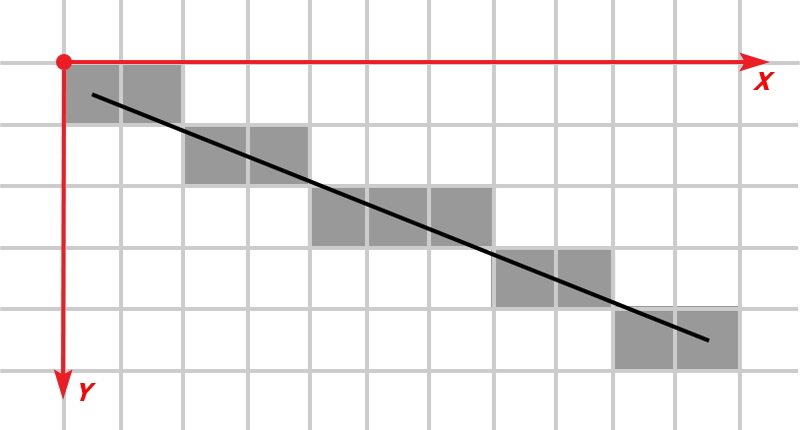
Bresenhamアルゴリズムは、2次元ラスタのどのポイントに色を付ける必要があるかを決定するアルゴリズムであり、2つの与えられたポイント間の直線を厳密に近似します。 アルゴリズムの本質は、各列X （図を参照）について、どの行Yが線に最も近いかを決定し、点を描くことです。
次に、同様のアルゴリズムが電気炉の発熱体の制御にどのように役立つかを見てみましょう。
ヒーターには220V / 50Hzの電圧が供給されます。 チャートを見てください。
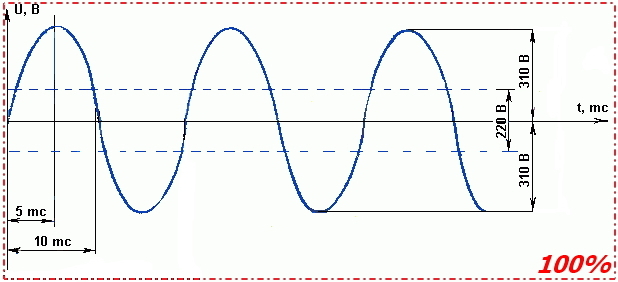
このような電圧を純粋な形で電気ヒーターの入力に印加すると、100％の加熱出力が得られます。 すべてがシンプルです。
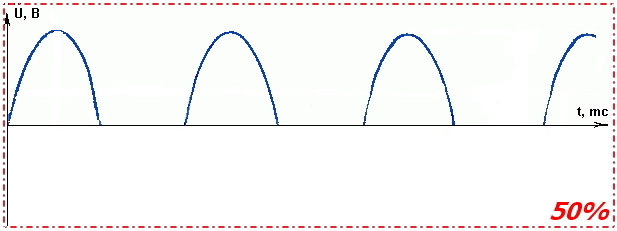
電源電圧の正の半波のみが発熱体の入力に印加されるとどうなりますか？ そうです、我々は加熱出力の50％を取得します。
3分の1ごとに半波を与えると、33％の電力が得られます。
例として、出力電力の10％のグラデーションと100msの時間スパンを考えます。これは、電源電圧の10半波に相当します。 10x10のグリッドを描き、 Y軸が出力電力値の軸であると想像します。 0から必要な電力値までの直線を描きます。
中毒を追跡しますか？
期間を1秒に増やすと、1％の出力電力のグラデーションを得ることができます。 それは、100x100のグリッドを意味します。
そして、心地よいものについて：
Bresenhamアルゴリズムは、 X軸に沿った各ステップで、現在のy値と現在のxの正確なy値との間の垂直距離を意味するエラー値を追跡できるように、ループで構築できます。 xを増やすたびに、傾きの量だけエラー値を増やします。 エラーが0.5を超える場合、ラインは次のyに近くなります。そのため、エラーを1減らしながら、 yを1つ増やします（読み取り-電圧の半波を1つスキップします）。
このアプローチは、周期的な整数加算に簡単に縮小できます（これについては、次の記事でMK演算アルゴリズムを説明するときに詳しく説明します）。
私は意図的に数式をロードしませんでした。 アルゴリズムは初歩的で、グーグルに簡単です。 回路での適用性を示したいだけです。 負荷を制御するには、ゼロ検出器を備えた一般的なMOC3063トライアック光結合配線図を使用します。
このアプローチには、多くの利点があります。
- 大きな負荷の頻繁な切り替えによるネットワークへの干渉は最小限であり、電圧がゼロを通過した瞬間にオン/オフの切り替えが発生します。
- 非常に単純なアルゴリズム-すべての計算は整数の処理になります。これはマイクロコントローラーに適しています。
- ゼロ電圧遷移検出器（hello MOC3063）をフェンスする必要はありません。 MKが単にタイマーを引き、フォトカプラーを開いたとしても、エラーは重大ではありません。
継続する。