少し前まで、同志メークマン は 、スペクトル分析が音響信号をその成分音に分解する方法を説明しました。 音から少し抽象化して、デジタル化された信号があり、そのスペクトル構成を決定し、非常に正確であると仮定します。
カットの下には、デジタルヘテロダインと少し特別なフーリエマジックを使用して、任意の信号から高調波を抽出する方法の簡単な概要があります。
私たちが持っているもの。
デジタル化された信号のサンプルを含むファイル。 信号は、正弦波とその周波数、振幅、初期位相、そして場合によってはホワイトノイズの合計であることが知られています。
何をしますか。
スペクトル分析を使用して以下を決定します。
- 信号構成の高調波の数、およびそれぞれの場合:振幅、周波数(以下、信号長あたりの波長数の文脈で)、初期位相。
- ホワイトノイズの有無、およびその標準偏差(標準偏差)の存在;
- 信号の定数成分の有無。
- これらすべてを
、ブラックジャックとイラスト付きの美しいPDFレポートで整理します。
Javaでこの問題を解決します。
マテリエル
すでに述べたように、信号の構造は既知です。これは、正弦波と何らかのノイズ成分の合計です。 エンジニアリングの実践における周期的信号の分析には、一般に「フーリエ分析」と呼ばれる強力な数学的装置が広く使用されています。 どんな動物なのか簡単に分析しましょう。
少し特別な、フーリエ魔法
少し前の19世紀に、フランスの数学者ジャンバプティストジョセフフーリエは、特定の条件(時間連続性、周期性、ディリクレ条件を満足する)を満たす関数を、一連の名前に拡張できることを示しました。
工学の実践では、フーリエ級数の周期関数の展開は、たとえば回路理論の問題で広く使用されています:非正弦波入力アクションは正弦波のアクションの合計に分解され、回路の必要なパラメーターは、たとえば重ね合わせ法によって計算されます
フーリエ級数の係数を書くためのいくつかの可能なオプションがあります、私たちは本質を知る必要があります。
フーリエ級数展開により、連続関数を他の連続関数の合計に展開できます。 そして一般的に、シリーズには無数のメンバーが含まれます。
フーリエアプローチのさらなる改良点は、彼自身の名前の積分変換です。 フーリエ変換 。
フーリエ級数とは異なり、フーリエ変換は、離散周波数(一般に、分解が離散的であるフーリエ級数の周波数のセット)ではなく連続で関数を分解します。
フーリエ級数の係数が、実際にスペクトルと呼ばれるフーリエ変換の結果にどのように関係しているか見てみましょう。
小さな余談:フーリエ変換のスペクトルは、一般的な場合、対応する高調波の複素振幅を記述する複素関数です。 つまり、スペクトルの値は複素数であり、そのモジュールは対応する周波数の振幅であり、引数は対応する初期位相です。 実際には、 振幅スペクトルと位相スペクトルは別々に考慮されます。

図 1.振幅スペクトルの例でのフーリエ級数とフーリエ変換の対応。
フーリエ級数の係数は、離散時刻におけるフーリエ変換の値に過ぎないことが容易にわかります。
ただし、フーリエ変換は、時間的に連続する無限関数を、周波数が連続する別の無限関数、つまりスペクトルにマッピングします。 時間的に無限の関数はなく、一部の離散部分のみが時間内に記録されている場合はどうなりますか? この質問に対する答えは、フーリエ変換のさらなる発展、すなわち離散フーリエ変換(DFT)によって与えられます。
離散フーリエ変換は、信号の時間における連続性と無限性の必要性の問題を解決するように設計されています。 実際、無限信号の一部を切り取ったと考えており、残りの時間領域では、この信号をゼロと見なします。
数学的には、これは研究対象の関数f(t)が無限にあることを意味し、それに何らかのウィンドウ関数w(t)を掛けます。
古典的なフーリエ変換の「出力」がスペクトル-関数である場合、離散フーリエ変換の「出力」は離散スペクトルです。 また、離散信号のサンプルも入力に送られます。
フーリエ変換の残りのプロパティは変更されません:それらは関連文献で読むことができます。
正弦波信号のフーリエ変換についてのみ知る必要があり、それをスペクトルで見つけようとします。 一般的な場合、これは、周波数領域のゼロ周波数に関して対称なデルタ関数のペアです。
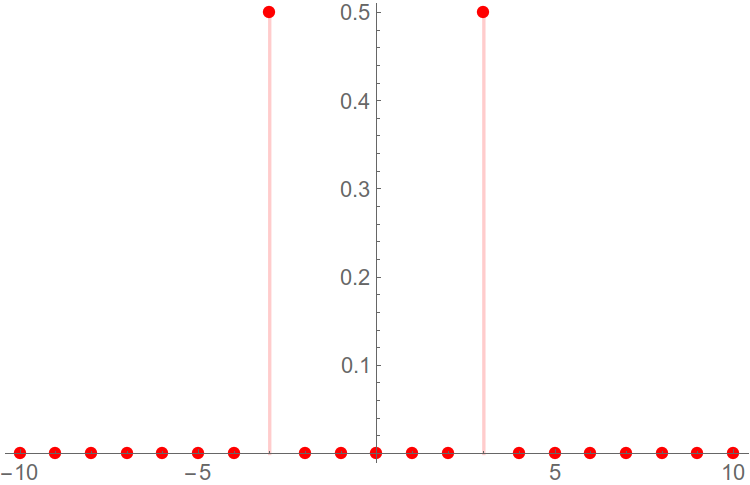
図 2.正弦波信号の振幅スペクトル。
一般的に言えば、私たちは元の関数ではなく、ウィンドウ関数を備えた製品の一部を検討していることを既に述べました。 次に、元の関数のスペクトルがF(w)で、ウィンドウがW(w)の場合、積スペクトルはこれら2つのスペクトルの畳み込み(F * W)(w)(畳み込み定理)のような不快な操作になります。
実際には、これは、デルタ関数の代わりに、スペクトルで次のようなものが表示されることを意味します。
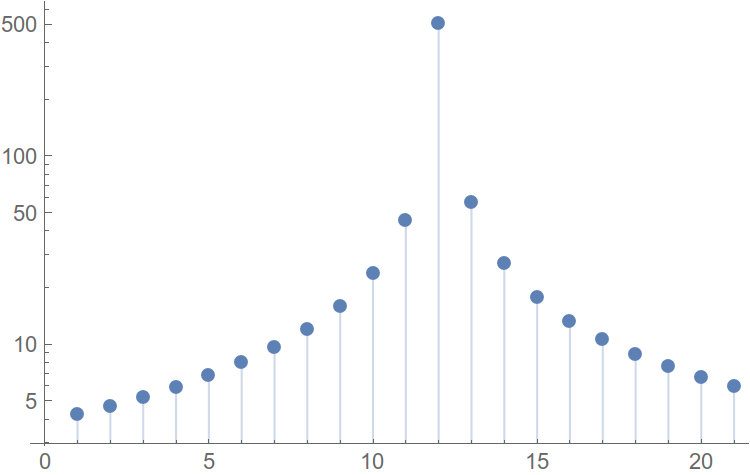
図 3.スペクトル拡散の効果。
この効果は、 スペクトル拡散 (Eng。Spectral Leekage)とも呼ばれます。 そして、それぞれサイドローブ (英語のサイドローブ)によるスペクトルの拡散により現れるノイズ。
サイドローブと戦うために、他の非長方形のウィンドウ関数が使用されます。 ウィンドウ関数の「効率」の主な特徴は、サイドローブのレベル (dB)です。 一般的に使用されるいくつかのウィンドウ関数のサイドローブレベルの概要表を以下に示します。
| ウィンドウ機能 | サイドローブレベル(dB) |
| ディリクレ窓(長方形窓) | -13 dB |
| 窓ハンナ | -31.5 dB |
| ハミングウィンドウ | -42 dB |
問題の主な問題は、サイドローブが近くにある他の高調波をマスクできることです。
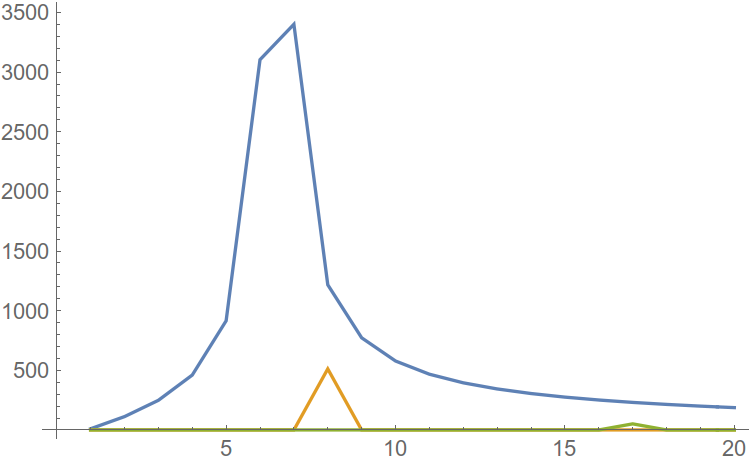
図 4.個別の高調波スペクトル。
スペクトルを加算すると、弱い高調波が強い高調波に溶解することがわかります。
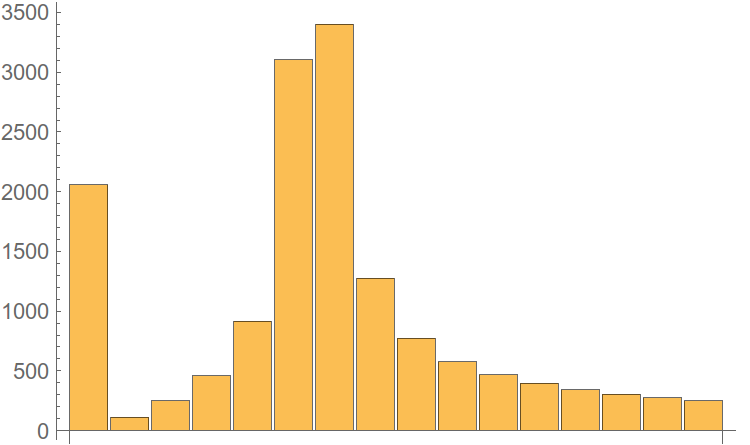
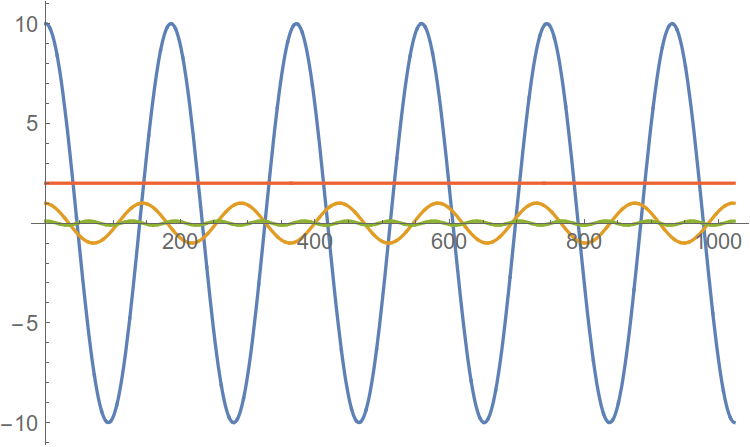
図 5. 1つの高調波のみがはっきりと見えます。 良くない
スペクトルの拡散を制御する別のアプローチは、この拡散を引き起こす高調波を信号から減算することです。
つまり、高調波の振幅、周波数、初期位相を設定することで、信号からそれを差し引くことができ、それに対応する「デルタ関数」と、それによって生成されるサイドローブを削除します。 もう1つの質問は、目的の高調波のパラメーターをどのように正確に知るかです。 複素振幅から必要なデータを取得するだけでは十分ではありません。 スペクトルの複素振幅は整数周波数で形成されますが、高調波が分数周波数を持つことを妨げるものは何もありません。 この場合、複素振幅は2つの隣接する周波数に分散しているようで、その正確な周波数は他のパラメーターと同様に確立できません。
目的の高調波の正確な周波数と複素振幅を確立するために、工学の実践の多くの分野で広く使用されている手法- ヘテロダインを使用します。
入力信号に複素調波Exp(I * w * t)を掛けるとどうなるか見てみましょう。 信号スペクトルはwを右にシフトします。
高調波がさらにデルタ関数に似るまで(つまり、特定のローカルS / N比が最大に達するまで)、信号のスペクトルを右にシフトすることにより、このプロパティを使用します。 次に、w 0 -w getとして目的の高調波の正確な周波数を計算し、元の信号から減算して、スペクトルの拡散効果を抑制します。
局部発振器の周波数に応じたスペクトルの変化の図を以下に示します。
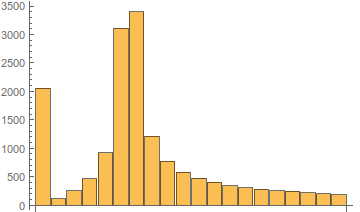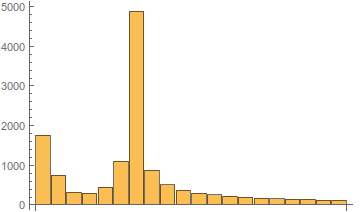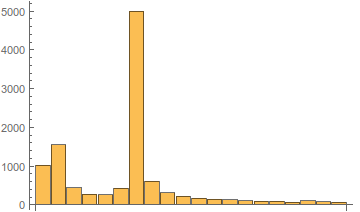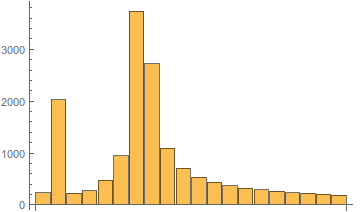
図 6.局部発振器の周波数に応じた振幅スペクトルのタイプ。
存在するすべての高調波を切り取るまで説明した手順を繰り返しますが、スペクトルはホワイトノイズのスペクトルを思い出させません。
次に、ホワイトノイズの標準偏差を評価する必要があります。 ここにはトリックはありません。単に式を使用して標準偏差を計算できます。
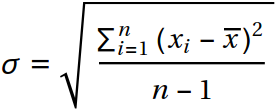
自動化する
高調波抽出を自動化するときが来ました。 アルゴリズムをもう一度繰り返しましょう。
1.特定のしきい値kを超える振幅スペクトルのグローバルピークを探しています。
1.1見つからない場合、終了
2.局部発振器の周波数を変化させることにより、特定の局部信号対雑音比の最大値がピークの特定の近傍で到達する周波数の値を探します
3.必要に応じて、振幅と位相の値を四捨五入します。
4.見つかった周波数、振幅、位相から局部発振器周波数を引いた信号から高調波を減算します。
5.ステップ1に進みます。
アルゴリズムは複雑ではなく、発生する唯一の質問は-高調波を探すしきい値をどこで取得するかです。
この質問に答えるには、高調波をカットする前でもノイズレベルを評価する必要があります。
分布関数(hi、mat。Statistics)を作成します。ここで、高調波の振幅は横軸になり、振幅を超えない高調波の数は、縦軸に沿った引数の値です。 そのような構築された関数の例:
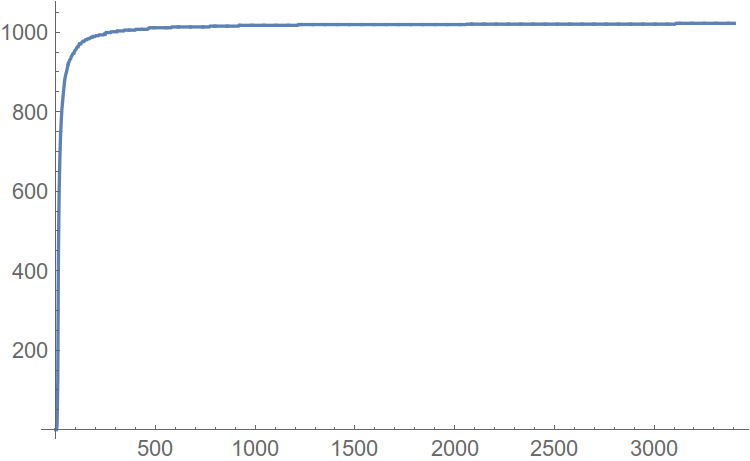
図 7.高調波分布関数。
また、分布密度という関数も作成します。 つまり、分布関数の有限差分の値。
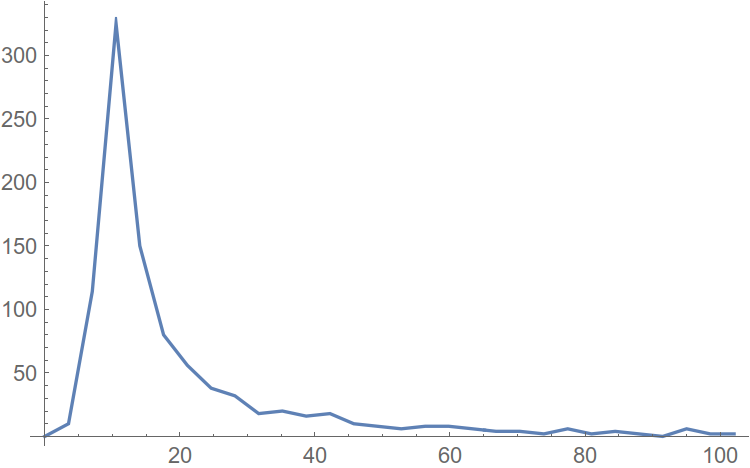
図 8.調和分布関数の密度。
分布密度の最大値の横軸は、スペクトル内で最大回数発生する高調波の振幅です。 ピークから特定の距離だけ右に移動し、この点の横座標をスペクトルのノイズレベルの推定値と見なします。 これで自動化できます。
信号の高調波を検出するコードを見てください
public ArrayList<SynthesizableSignal> detectHarmonics() { SignalCutter cutter = new SignalCutter(source, new Signal(source)); SynthesizableComplexExponent heterodinParameter = new SynthesizableComplexExponent(); heterodinParameter.setProperty("frequency", 0.0); Signal heterodin = new Signal(source.getLength()); Signal heterodinedSignal = new Signal(cutter.getCurrentSignal()); Spectrum spectrum = new Spectrum(heterodinedSignal); int harmonic; while ((harmonic = spectrum.detectStrongPeak(min)) != -1) { if (cutter.getCuttersCount() > 10) throw new RuntimeException("Unable to analyze signal! Try another parameters."); double heterodinSelected = 0.0; double signalToNoise = spectrum.getRealAmplitude(harmonic) / spectrum.getAverageAmplitudeIn(harmonic, windowSize); for (double heterodinFrequency = -0.5; heterodinFrequency < (0.5 + heterodinAccuracy); heterodinFrequency += heterodinAccuracy) { heterodinParameter.setProperty("frequency", heterodinFrequency); heterodinParameter.synthesizeIn(heterodin); heterodinedSignal.set(cutter.getCurrentSignal()).multiply(heterodin); spectrum.recalc(); double newSignalToNoise = spectrum.getRealAmplitude(harmonic) / spectrum.getAverageAmplitudeIn(harmonic, windowSize); if (newSignalToNoise > signalToNoise) { signalToNoise = newSignalToNoise; heterodinSelected = heterodinFrequency; } } SynthesizableCosine parameter = new SynthesizableCosine(); heterodinParameter.setProperty("frequency", heterodinSelected); heterodinParameter.synthesizeIn(heterodin); heterodinedSignal.set(cutter.getCurrentSignal()).multiply(heterodin); spectrum.recalc(); parameter.setProperty("amplitude", MathHelper.adaptiveRound(spectrum.getRealAmplitude(harmonic))); parameter.setProperty("frequency", harmonic - heterodinSelected); parameter.setProperty("phase", MathHelper.round(spectrum.getPhase(harmonic), 1)); cutter.addSignal(parameter); cutter.cutNext(); heterodinedSignal.set(cutter.getCurrentSignal()); spectrum.recalc(); } return cutter.getSignalsParameters(); }
実用部
私はJavaの専門家のふりをしてはいません。提示されたソリューションは、パフォーマンスとメモリ消費の両方、そして一般的にJava哲学とOOP哲学の両方の点で疑わしいかもしれません。 コンセプトの証明として、数晩で書かれました。 興味がある人はGitHubでソースコードを読むことができます。
唯一の難しさは、分析結果に基づいたPDFレポートの生成でした。PDFboxは、キリル文字を使用することを決して望んでいませんでした。 ところで、彼は今それを望んでいません。
プロジェクトはライブラリを使用しました:
JFreeChart-チャート表示
PDFBox-レポート作成
JLatexMath-ラテックス式のレンダリング
その結果、タスクを便利に実装するかなり大規模なプログラム(13.6メガバイト)を手に入れました。
高調波を手動で切り取り、このタスクをアルゴリズムに任せることができます。
ご清聴ありがとうございました!
プログラムによって作成されたレポートの例 。
文学
Sergienko A. B.-デジタル信号処理