CPUとGPUを使用したMSTアルゴリズムのハイブリッド実装

はじめに

最小全域木（MST-最小全域木）の検索の問題を解決することは、さまざまな研究分野における一般的なタスクです：さまざまなオブジェクトの認識、コンピュータービジョン、ネットワークの分析と構築（電話、電気、コンピューター、道路など）、化学そして生物学と他の多くの。 この問題を解決する少なくとも3つの有名なアルゴリズムがあります：Boruvki、KruskalおよびPrima。 大きなグラフ（数GBを占める）の処理は、中央処理装置（CPU）にとってかなり時間がかかるタスクであり、現時点では需要があります。 CPUよりもはるかに優れたパフォーマンスを発揮できるグラフィックアクセラレータ（GPU）が普及しています。 しかし、多くのグラフ処理タスクと同様に、MSTタスクはGPUアーキテクチャにうまく適合しません。 この記事では、GPUでのこのアルゴリズムの実装について説明します。 また、CPUを使用して、1つのノード（GPUと複数のCPUで構成される）の共有メモリ上でこのアルゴリズムのハイブリッド実装を構築する方法も示します。

グラフ表示形式の説明

将来的に言及され、変換されるため、無向加重グラフのストレージ構造を簡単に検討します。 グラフは、圧縮CSR（圧縮スパース行） [1]形式で設定されます。 この形式は、疎行列とグラフの保存に広く使用されています。 N個の頂点とM個のエッジを持つグラフの場合、X、A、およびWの3つの配列が必要です。サイズN + 1の配列X、他の2つは2 * Mです。頂点の任意のペアの無向グラフでは、直接アークと逆アークを保存する必要があるためです。 配列Xは、配列Aに格納されているネイバーのリストの最初と最後を格納します。つまり、頂点Jのネイバーのリスト全体は、インデックスX [J]からX [J + 1]までの配列Aにあります。 頂点Jからの各エッジの重みは、同様のインデックスによって保存されます。説明のために、下の図は、隣接行列と右側のCSR形式を使用して記述された6つの頂点のグラフを示しています（簡単にするため、各エッジの重みは示していません）。

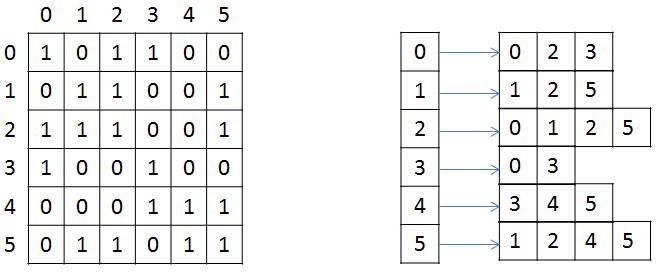
テスト済みグラフ

変換アルゴリズムとMSTアルゴリズムの説明には問題のグラフの構造の知識が必要になるため、テストが行​​われたグラフについてすぐに説明します。 実装パフォーマンスを評価するために、RMATグラフとSSCA2グラフの2種類の合成グラフが使用されます。 R-MAT-グラフは、ソーシャルネットワーク、インターネット[2]からの実際のグラフをうまくモデル化します。 この場合、頂点32の平均連結度を持つRMATグラフを検討し、頂点の数は2のべき乗です。 このようなRMATグラフには、1つの大きな連結コンポーネントと、多数の小さな連結コンポーネントまたは垂れ下がった頂点があります。 SSCA2-graphは、エッジで互いに接続された独立したコンポーネントの大きなセットです[3] 。 SSCA2グラフは、頂点の平均接続度が32に近く、その頂点の数も2のべき乗になるように生成されます。 したがって、2つの完全に異なるグラフが考慮されます。

入力変換

アルゴリズムのテストは、ジェネレーターを使用して取得されたグラフRMATおよびSSCA2で実行されるため、アルゴリズムのパフォーマンスを改善するにはいくつかの変換が必要です。 すべてのコンバージョンはパフォーマンス計算に含​​まれません。

1. 頂点のリストをローカルで並べ替える
   
   各頂点について、重みの隣接リストを昇順で並べ替えます。 これにより、アルゴリズムの各反復での最小エッジの選択が部分的に簡素化されます。 このソートはローカルであるため、問題の完全な解決策を提供しません。
   
   
2. グラフのすべての頂点の番号を付け直す
   
   最も接続された頂点が最も近い番号を持つように、グラフの頂点に番号を付けます。 この操作の結果、接続された各コンポーネントで、最大頂点数と最小頂点数の差が最小になり、小さなグラフィックスプロセスキャッシュを最大限に活用できます。 RMATグラフの場合、この最適化を適用した後でもこのグラフにはキャッシュに収まらない非常に大きなコンポーネントがあるため、RMATグラフの場合、この番号付けの変更は大きな影響を与えません。 SSCA2グラフの場合、このグラフには小さなコンポーネントが多数あるため、この変換の効果はより顕著です。
   
   
3. グラフの重みを整数にマッピングする
   
   この問題では、グラフの重みに対して操作を実行する必要はありません。 2つのrib骨の重量を比較できる必要があります。 これらの目的には、GPUでの単精度数値の処理速度が2倍よりはるかに速いため、倍精度数値の代わりに整数を使用できます。 この変換は、一意のエッジの数が2 ^ 32（符号なしintに収まる異なる数の最大数）を超えないグラフに対して実行できます。 各頂点の平均接続度が32 mの場合、この変換を使用して処理できる最大のグラフは2 ^ 28個の頂点を持ち、メモリで64 GBを占有します。 現在まで、アクセラレータNVidia Tesla k40 [4] / NVidia Titan X [5]およびAMD FirePro w9100 [6]の最大メモリ量は、それぞれ12GBおよび16GBです。 したがって、この変換を使用する単一のGPUで、非常に大きなグラフを処理できます。
   
   
4. 頂点圧縮
   
   この変換は、構造が原因でSSCA2グラフにのみ適用されます。 このタスクでは、すべてのレベルのメモリパフォーマンスが決定的な役割を果たします。グローバルメモリから1次キャッシュまでです。 グローバルメモリとL2キャッシュ間のトラフィックを減らすために、頂点情報を圧縮形式で保存できます。 最初に、頂点に関する情報は2つの配列の形式で表示されます。配列Xは、配列Aの隣接リストの開始と終了を格納します（1つの頂点のみの例）。
   
   
   
   頂点Jには10個のネイバー頂点があり、各ネイバーの数がunsigned int型を使用して格納される場合、J頂点のネイバーのリストを格納するには10 * sizeof（unsigned int）バイトが必要で、2 * M * sizeof（グラフ全体に対して符号なし） int）バイト。 sizeof（unsigned int）= 4バイト、sizeof（unsigned short）= 2バイト、sizeof（unsigned char）= 1バイトと仮定します。 次に、この頂点について、隣接リストを保存するために40バイトが必要です。
   
   このリストの頂点の最大数と最小数の差が8であり、この数を格納するために必要なのは4ビットだけであることに気付くのは難しくありません。 頂点の最大数と最小数の差がunsigned intより小さい可能性があるという考慮事項に基づいて、次のように各頂点の数を表すことができます。
   
   base_J + 256 * k + short_endV、
   
   base_Jは、たとえば、隣接リスト全体の最小頂点番号です。 この例では、1になります。この変数はunsigned int型であり、グラフ内の頂点と同じ数の変数があります。 次に、頂点番号と選択したベースの差を計算します。 最小のピークをベースとして選択したため、この差は常に正になります。 SSCA2の場合、この差は符号なしショートに置かれます。 short_endVは、256で除算した残りの部分です。この変数を格納するには、unsigned char型を使用します。 kは 256で割った整数部分です。kの場合、2ビットを選択します（つまり、kは0〜3の範囲にあります）。 問題のグラフには、選択した表現で十分です。 ビット表現では、次のようになります。
   
   
   
   したがって、頂点のリストを格納するには、この例では、40バイトではなく（1 + 0.25）* 10 + 4 = 16.5バイトが必要であり、グラフ全体では（2 * M + 4 * N + 2 * M / 4 ）の代わりに2 * M *4。N= 2 * M / 32の場合、合計音量は
   
   （8 * M）/（2 * M + 8 * M / 32 + 2 * M / 4） = 2.9回
   
   

アルゴリズムの一般的な説明

MSTアルゴリズムを実装するために、Boruwkaアルゴリズムが選択されました。 Boruwkaアルゴリズムの基本的な説明とその反復の説明は、ここ[7]で十分に説明されています。

アルゴリズムによれば、すべての頂点は最初に最小ツリーに含まれます。 次に、次の手順を完了する必要があります。

1. 後続の結合のために、すべてのツリー間の最小エッジを見つけます。 このステップでエッジが選択されていない場合、問題に対する答えが受け取られます
2. 一致するツリーをマージします。 このステップは2つの段階に分かれています。2つのツリーがマージの候補として相互に示すことができるため、サイクルを削除することと、結合されたサブツリーを含むツリーの数が選択された場合のマージステップです。 明確にするために、最小数を選択します。 マージ中にツリーが1つしか残っていない場合、問題に対する答えが返されます。
3. 結果のツリーに番号を付け直して最初のステップに進みます（すべてのツリーに0からkまでの番号が付けられるように）

アルゴリズムの段階

一般に、実装されるアルゴリズムは次のとおりです。



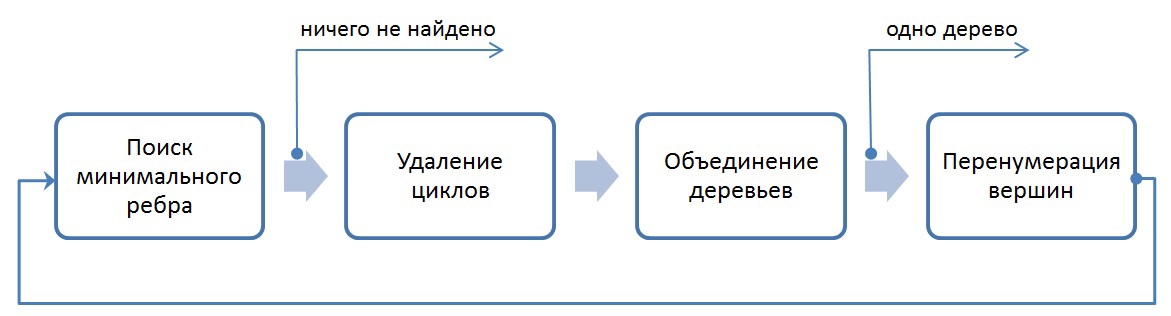
アルゴリズム全体の抜け道は2つの場合に発生します：N回の反復後のすべての頂点が1つのツリーに結合される場合、または各ツリーから最小エッジを見つけることができない場合（この場合、最小スパニングツリーが検出されます）。

1.最小エッジを検索します。

まず、グラフの各頂点が個別のツリーに配置されます。 次に、上記の4つの手順で構成されるツリーを結合する反復プロセスが発生します。 最小エッジを見つける手順により、最小スパニングツリーに含まれるエッジを正確に選択できます。 上記のように、この手順の入力時に、変換されたグラフはCSR形式で保存されます。 エッジは隣接リストの重みで部分的にソートされているため、最小頂点を選択すると、隣接リストを表示し、別のツリーに属する最初の頂点を選択することになります。 グラフにループがないと仮定した場合、アルゴリズムの最初のステップで、最小頂点を選択すると、考慮中の各頂点の隣接リストから最初の頂点が選択されます。これは、隣接頂点のリスト（グラフのエッジと考慮中の頂点を含む）が重みの増加によってソートされるためですエッジと各頂点は別々のツリーに入ります。 他のステップでは、隣接するすべての頂点のリストを順番に表示し、別のツリーに属する頂点を選択する必要があります。



隣接する頂点のリストから2番目の頂点を選択し、このエッジを最小にすることができないのはなぜですか？ ツリーを結合する手順（後で検討します）の後に、隣接するもののリストからいくつかの頂点が検討中の頂点と同じツリーに表示される場合があります。これにより、このエッジはこのツリーのループになり、アルゴリズムの条件により、最小エッジを選択する必要があります他の木に。



Union Implement [8]は 、頂点処理を実装し、検索、マージ、およびマージリストを実行するのに適しています。 残念ながら、すべての構造がGPUで最適に処理されるわけではありません。 このタスクで最も有益なのは（他のほとんどの場合と同様）、リンクリストの代わりにGPUメモリで連続配列を使用することです。 以下では、グラフ内の最小エッジを見つけ、セグメントを結合し、サイクルを削除するための同様のアルゴリズムを検討します。



最小エッジを見つけるアルゴリズムを検討してください。 次の2つの手順で表すことができます。

• 問題のグラフの各頂点（セグメントに含まれる）から出る最小エッジの選択。
• 各ツリーの最小重みのエッジの選択。

CSR形式で記録された頂点情報を移動しないようにするために、2つの補助配列を使用して、隣接リストの配列Aの最初と最後のインデックスを保存します。 指定された2つの配列は、1つのツリーに属する頂点リストのセグメントを示します。 たとえば、最初のステップでは、開始値または下限値の配列の値は配列Xの0..Nになり、終了値の配列または上限値の値は配列Xの1..N + 1になります。そして、ツリーを結合する手順の後）、これらのセグメントは混合されますが、メモリ内のネイバーAの配列は変更されません。



両方のステップを並行して実行できます。 最初のステップを完了するには、各頂点（または各セグメント）の隣接リストを見て、別のツリーに属する最初のエッジを選択する必要があります。 1つのワープ（32スレッドで構成される）を選択して、各頂点の隣接リストを表示できます。 隣接するピークAの配列のいくつかのセグメントが行になく、1つのツリーに属していることを覚えておく価値があります（ツリー0に属するセグメントは赤で強調表示され、ツリー1は緑で強調表示されます）。



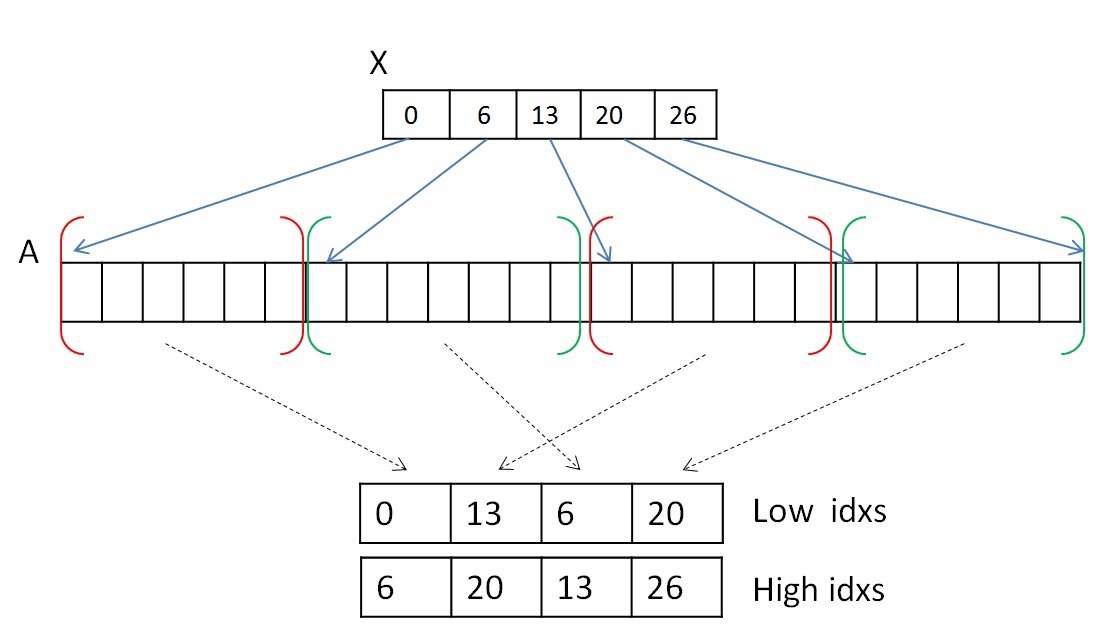
隣接リストの各セグメントはソートされているため、すべての頂点を表示する必要はありません。 1つのワープは32のスレッドで構成されるため、表示は32の頂点の部分で行われます。 32個の頂点を表示した後、結果を結合する必要があり、何も見つからない場合は、次の32個の頂点を表示します。 結果を組み合わせるには、スキャンアルゴリズムを使用できます[9] 。 共有メモリまたは新しいshfl命令[10] （Keplerアーキテクチャから入手可能）を使用して、1つのワープ内にこのアルゴリズムを実装できます。これにより、1つの命令で1つのワープのスレッド間でデータを交換できます。 実験の結果、shfl命令はアルゴリズム全体の作業を約2倍高速化できることが判明しました。 したがって、この操作は、たとえば次のようにshfl命令を使用して実行できます。

unsigned idx = blockIdx.x * blockDim.x + threadIdx.x; //    unsigned lidx = idx % 32; #pragma unroll for (int offset = 1; offset <= 16; offset *= 2) { tmpv = __shfl_up(val, (unsigned)offset); if(lidx >= offset) val += tmpv; } tmpv = __shfl(val, 31); //     .    1,  -   //  ,    .
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このステップの結果、各セグメントについて次の情報が記録されます。最小重みのエッジに含まれる配列Aの頂点の数とエッジ自体の重み。 何も見つからない場合は、たとえば、頂点番号にN + 2の数を書き込むことができます。



2番目のステップは、選択した情報、つまり各ツリーの最小重みを持つエッジの選択を減らすために必要です。 同じツリーに属するセグメントは、並行して独立してスキャンされ、各セグメントに対して最小重みエッジが選択されるため、このステップが実行されます。 このステップでは、1つのワープで各ツリーの情報を（複数のセグメントについて）削減でき、shfl命令も削減に使用できます。 この手順を完了すると、各ツリーが最小エッジ（存在する場合）によってどのツリーに接続されているかがわかります。 この情報を記録するために、さらに2つの補助配列を導入します。1つは、最小エッジが存在するまでのツリーの数を格納します。2つ目は、元のグラフの頂点の数で、ツリーに入る頂点のルートです。 この手順の結果を以下に示します。



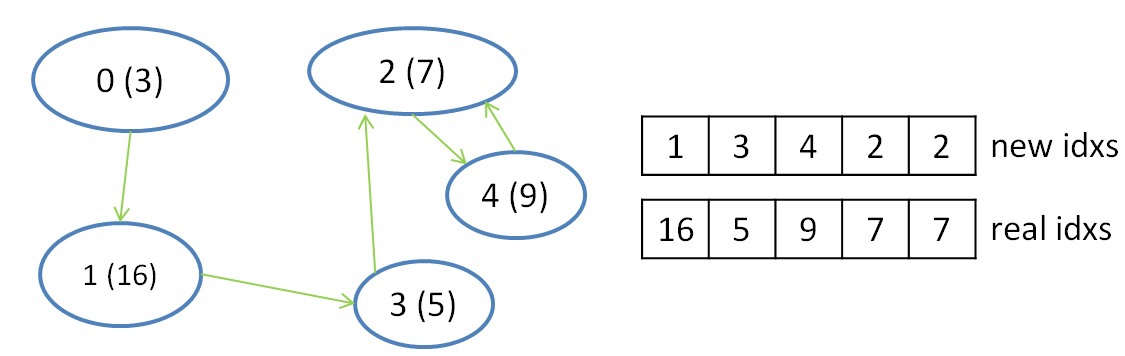
インデックスを操作するには、さらに2つの配列が必要です。これは、元のインデックスを新しいインデックスに変換し、新しいインデックスを使用して元のインデックスを取得するのに役立ちます。 これらのいわゆるインデックス変換テーブルは、アルゴリズムの各反復で更新されます。 初期インデックスによって新しいインデックスを取得するためのテーブルのサイズはN-グラフ内の頂点の数であり、初期インデックスを取得するためのテーブルは各反復で新しい方法で縮小され、アルゴリズムの選択された反復でのツリーの数に等しいサイズを持ちます（アルゴリズムの最初の反復では、このテーブルもサイズN）。

2.サイクルを削除します。

この手順は、2つのツリー間のループを削除するために必要です。 この状況は、ツリーN1の最小エッジがツリーN2にあり、ツリーN2の最小エッジがツリーN1にある場合に発生します。 上の図では、番号2と4の2つのツリー間にのみサイクルがあります。各反復でツリーが少ないため、サイクルを構成する2つのツリーの最小数を選択します。 この場合、2は2を指し、4は2を指し続けます。これらのチェックを使用して、このようなサイクルを決定し、最小数を優先して排除することができます。

  unsigned i = blockIdx.x * blockDim.x + threadIdx.x; unsigned local_f = F[i]; if (F[local_f] == i) { if (i < local_f) { F[i] = i; . . . . . . . } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この手順は、各頂点を独立して処理でき、サイクルのない頂点の新しい配列のレコードが交差しないため、並行して実行できます。

3.木の結合。

この手順では、ツリーをより大きなツリーに結合します。 2つのツリー間のループを削除する手順は、基本的にこの手順の前の前処理です。 ツリーをマージするときのループを回避します。 ツリーの結合は、リンクを変更して新しいルートを選択するプロセスです。 たとえば、ツリー0がツリー1を指し、ツリー1がツリー3を指している場合、ツリー0のリンクをツリー1からツリー3に変更できます。このリンクの変更は、リンクを変更しても2つのツリー間のループが発生しない場合に価値があります。 上記の例を考慮すると、サイクルの削除とツリーの結合後、2番のツリーが1つだけ残ります。結合プロセスは次のように表すことができます。



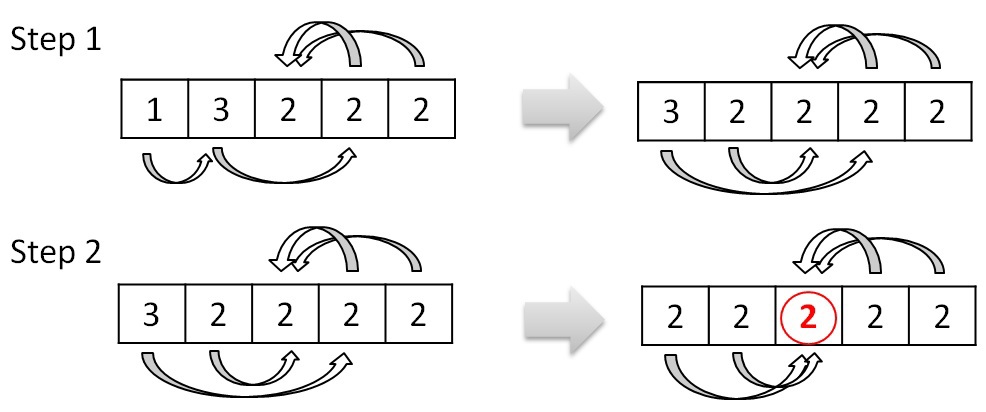
グラフの構造とその処理の原理は、プロシージャがループする状況がなく、並行して実行できるようなものです。

4.ピーク（ツリー）の番号を付け直します。

マージ手順を実行した後、結果のツリーに番号を付け直して番号が0からPになるようにする必要があります。構築により、新しい番号は条件F [i] == iを満たす配列要素を受け取る必要があります（上記の例では、要素のみがこの条件を満たすインデックス2）。 したがって、アトミック操作を使用すると、1 ...（P + 1）の新しい値で配列全体をマークできます。 次に、新しいインデックスの初期インデックスと初期インデックスの新しいインデックスを取得するための表を完成させます。



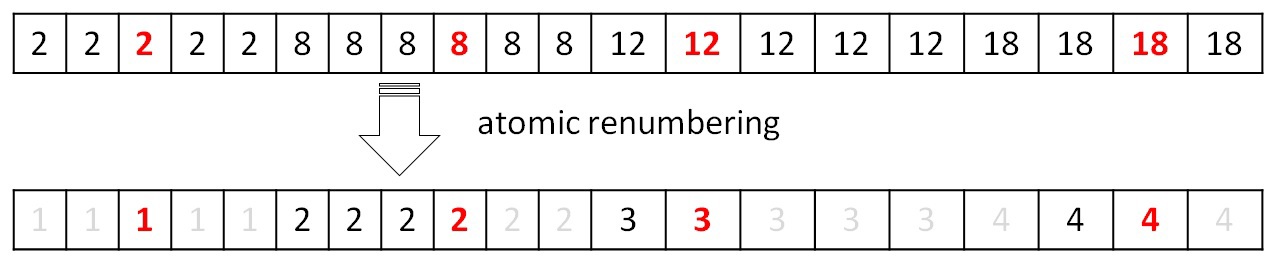
これらのテーブルの操作については、最小エッジを見つける手順で説明しています。 テーブルデータを更新しないと、次の反復を正しく実行できません。 説明されているすべての操作は、GPU上で並行して実行されます。



短い要約を要約する 。 4つの手順はすべて、並行してグラフィックアクセラレータで実行されます。 作業は1次元配列で行われています。 唯一の難点は、これらのすべての手順に間接的なインデックス付けがあることです。 また、このような配列の処理によるキャッシュミスを減らすために、最初に説明したグラフのさまざまな順列が使用されました。 しかし、残念なことに、すべてのグラフが間接インデックス作成による損失を削減するわけではありません。 後で示すように、このアプローチでは、RMATグラフは非常に高いパフォーマンスを達成しません。 最小エッジを見つけるには、アルゴリズム全体が機能する時間の80％までかかり、残りは残りの20％を占めます。 これは、ループの結合、削除、および番号の付け直しの手順で、長さが絶えず減少する配列（反復から反復へ）で作業が行われるという事実によるものです。 考慮されるグラフでは、約7〜8回の反復を行う必要があります。 これは、最初のステップですでに処理される頂点の数がN / 2よりはるかに少なくなることを意味します。最小エッジを見つけるためのメイン手順では、頂点Aの配列と重みWの配列で作業が行われます（特定の要素が選択されます）。

グラフの保存に加えて、長さNの配列がさらにいくつか使用されました。

• 低い値の配列と高い値の配列。 配列Aのセグメントを操作するために使用されます。
• 新しいインデックスの元のインデックスを取得する配列テーブル。
• オリジナルの新しいインデックスを取得する配列テーブル。
• 頂点番号の配列とそれらに対応する重みの配列。これらは最小エッジ検索手順の2番目のステップで使用されます。
• 手順の最初のステップで、このツリーまたはそのセグメントが属するツリーの最小エッジを見つけるための補助配列。

最小エッジ検索手順のハイブリッド実装。

上記のアルゴリズムは、最終的に単一のGPUでパフォーマンスが低下することはありません。 この問題の解決策は、CPU上でもこの手順を並列化できるように編成されています。 もちろん、これは共有メモリでのみ行うことができ、このためにOpenMP標準を使用し、PCIeバスを介してCPUとGPUの間でデータを転送しました。 タイムラインでの1回の繰り返しでのプロシージャの実行を想像すると、1つのGPUを使用するときの図は次のようになります。



最初は、すべてのグラフデータがCPUとGPUの両方に保存されます。 CPUが読み取れるようにするには、ツリーのマージ中に移動したセグメントに関する情報を送信する必要があります。 また、GPUがアルゴリズムの反復を継続するには、計算されたデータを返す必要があります。 ホストとアクセラレータ間で非同期コピーを使用することは論理的です：



CPUのアルゴリズムはGPUで使用されるアルゴリズムを繰り返し、OpenMPのみがループの並列化に使用されます[11] 。 予想どおり、CPUはGPUほど速くカウントされず、コピーのオーバーヘッドも干渉します。 CPUがその部分を計算するには、計算データを1：5の比率で分割する必要があります。つまり、CPUに転送されるのは20％〜25％のみで、残りはGPUで計算する必要があります。 残りの手順は、時間がかからず、オーバーヘッドとCPU速度の低下がアルゴリズム時間を増加させるだけなので、あちこちを読むのに有利ではありません。 CPUとGPU間のコピー速度も非常に重要です。 テストされたプラットフォームは、PCIe 3.0をサポートしており、12GB / sに到達できました。



これまでのところ、GPUとCPUのRAMの量は大きく異なり、後者の方が有利です。 テストプラットフォームでは、6 GB GDDR5がインストールされましたが、CPUでは48 GBもありました。 GPUのメモリ制限により、大きなグラフを計算できません。 そして、CPUとユニファイドメモリテクノロジー[12]は、CPUメモリからGPUにアクセスすることを可能にします。 グラフに関する情報は最小エッジを見つけるための手順でのみ必要であるため、大きなグラフの場合、最初にすべての補助配列をGPUメモリに配置し、次にグラフ配列の一部（隣接配列A、配列Xおよび重みWの配列）をメモリに配置できますGPU、しかし適合しなかったもの-CPUのメモリ内。 さらに、計算中に、GPUに適合しなかった部分がCPUで処理されるようにデータを分割することができ、GPUはCPUメモリへのアクセスを最小限に使用します（グラフィックアクセラレータからCPUメモリへのアクセスはPCIeバスを介して、 15 GB /秒）。 データがどの割合で分割されているかは事前にわかっているため、GPUまたはCPUでアクセスするメモリを決定するには、配列が分離されるポイントを示す定数を入力するだけで十分で、GPUのアルゴリズムを1回チェックするだけでどこで実行するかを決定できますアピール。 これらの配列のメモリ内の場所は、おおよそ次のように表すことができます。



したがって、記載されている圧縮アルゴリズムを使用しても、GPUに最初は収まらないグラフを処理できますが、PCIeのスループットは非常に限られているため、より低い速度で処理できます。

試験結果

テストは、192個のcudaコア（合計2688）を備えた14個のSMXと、3.7 GHzの周波数を備えた6個のコア（12番目）のIntel Xeon E5 v1660プロセッサを備えたNVidia GTX Titan GPUで実行されました。 テストが実行されたグラフは上記のとおりです。 いくつかの特徴のみを示します。

スケール（2 ^ N）	頂点の数	リブの数（2 * M）		グラフサイズ、GB
		RMAT	SSCA2
16	65,536	2,097 152	〜2 100 000	〜0.023
21	2,097 152	67 108 864	〜67,200,000	〜0.760
24	16 777 216	536 870 912	〜537百万	〜6.3
25	33554432	1,073,741,824	〜1,075,000,000	〜12.5
26	67108864	2 147 483 648	〜2 150 000 000	〜25.2
27	134 217 728	4,294,967,296	〜4,300,000,000	〜51.2

スケール16のグラフは非常に小さく（約25 MB）、変換なしでも1つの最新のIntel Xeonプロセッサのキャッシュに簡単に収まることがわかります。 グラフの重みは合計の2/3を占めるため、実際には約8 MBを処理する必要がありますが、これはL2 GPUキャッシュの約5倍にすぎません。 ただし、大きなグラフには十分な量のメモリが必要であり、スケール24のグラフでさえ、圧縮せずにテスト済みGPUのメモリに収まらなくなります。 グラフ表現に基づいて、26番目のスケールは最後のスケールで、エッジの数が符号なし整数に配置されます。これは、さらにスケーリングするためのアルゴリズムの制限です。 この制限は、データ型を拡張することで簡単に回避できます。 これは、単精度（unsigned int）の処理がdouble（unsigned long long）よりも何倍も高速であり、メモリの量がまだ非常に少ないため、これまでのところそれほど関連していないようです。 パフォーマンスは、1秒あたりに処理されるエッジの数で測定されます（1秒あたりの通過エッジ-TEPS）。



コンパイルは、オプション-O3 -arch = sm_35のNVidia CUDA Toolkit 7.0を使用して、オプション-O3のIntel Composer 2015を使用して実行されました。 実装されたアルゴリズムの最大パフォーマンスは、以下のグラフで見ることができます：



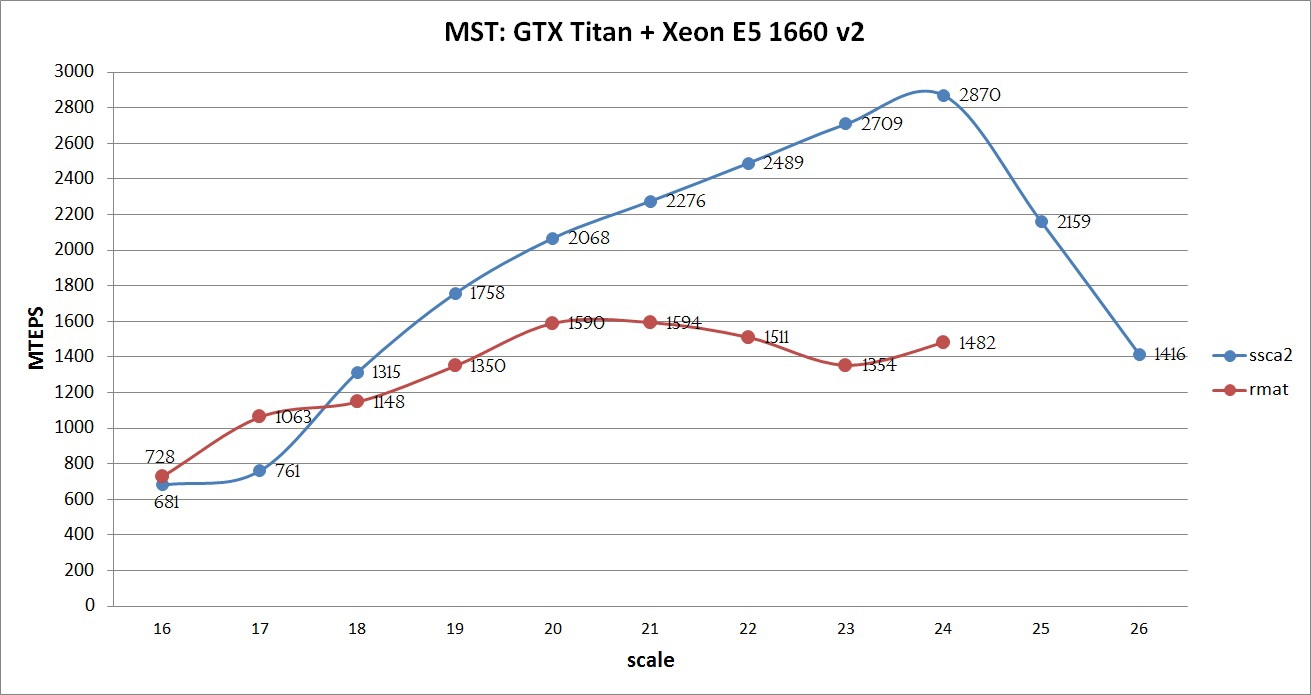
グラフは、すべてのSSCA2最適化を使用して、グラフが良好なパフォーマンスを示していることを示しています。グラフが大きいほど、パフォーマンスが向上しています。 この成長は、すべてのデータがGPUのメモリに配置されるまで維持されます。 25スケールと26スケールでは、Unified Memoryメカニズムが使用されました。これにより、速度は低下しますが、結果を得ることができました（ただし、以下に示すように、CPUのみより高速です）。 12 GBのメモリを搭載し、ECCとIntel Xeon E5 V2 / V3プロセッサを無効にしたTesla k40で計算を実行した場合、スケール25のSSCA2グラフで約3000 MTEPSを達成でき、26スケールのグラフだけでなく、 27.このような実験は、その複雑な構造とアルゴリズムの不十分な適応のために、RMATグラフでは実施されませんでした。

さまざまなアルゴリズムのパフォーマンスの比較

この問題は、GraphHPC 2015カンファレンスのコンペティションの枠組みで解決されましたが、著者によると、このコンペティションで1位になったAlexander Daryinによって書かれたプログラムと比較したいと思います。

一般的な表には、作成者が提供したテストプラットフォームの結果が含まれているため、説明したプラットフォーム（GTX Titan + Xeon E5 v2）のCPUおよびGPUにグラフィックスを配置するのは適切です。 以下は、2つのグラフの結果です。







グラフから、この記事で説明したアルゴリズムはSSCA2グラフに対してより最適化されているのに対し、Alexander Daryinによって実装されたアルゴリズムはRMATグラフに対して最適化されていることがわかります。 この場合、どの実装が最良であるかを明確に言うことは不可能です。それぞれに独自の長所と短所があるためです。 また、アルゴリズムを評価する基準は明確ではありません。 大きなグラフの処理について話す場合、アルゴリズムが24〜26スケールのグラフを処理できるという事実は大きなプラスであり、利点です。 任意のサイズのグラフの平均処理速度について話す場合、どの平均値を考慮するかは明確ではありません。 明確なことは1つだけです。1つのアルゴリズムはSSCA2グラフを適切に処理し、2番目はRMATです。 これら2つの実装を組み合わせた場合、平均パフォーマンスは23スケールで約3200 MTEPSになります。 ここでアレクサンダーダリンアルゴリズムのいくつかの最適化の記述のプレゼンテーションを見つけることができます 。



外国の記事から、次のものを区別することができます。

1） [13]この記事から、説明したアルゴリズムの実装にいくつかのアイデアが使用されました。 古いNVidia Tesla S1070でテストが行​​われたため、著者によって得られた結果を直接比較することはできません。 著者がGPUで達成したパフォーマンスは18〜36 MTEPSの範囲です。 2009年と2013年に公開。

2） [14] GPUでのPrimアルゴリズムの実装。

3） [15] GPUでのk NN-Boruvkaの実装。

CPUにはいくつかの並列実装もあります。 しかし、外国の記事では高いパフォーマンスを見つけることができませんでした。 たぶん、読者の一人が私が何かを見逃したかどうかを知ることができるでしょう。 また、ロシアではこのトピックに関する出版物がほとんどないことも注目に値します（ Vadim Zaitsevを除く）。これは非常に悲しいことです。

競争について、そして結論ではなく

私は、過去について述べ、MSTの最良の実装のための競争について言及したいと思います。 これらのメモを読んで、私の個人的な意見を述べる必要はありません。 誰かが非常に異なった考え方をしている可能性があります。



すべての参加者についてこの問題を解決するための基礎は、実際には同じBoruvkaアルゴリズムに基づいていました。 他のアルゴリズム（KruskalaおよびPrima）の計算は非常に複雑で、GPUなどの並列アーキテクチャにマッピングが遅いか不十分であるため、タスクは少し簡略化されています。 会議の名前から論理的には、メモリ内で1 GB以上を占めるようなグラフ（22以上のスケールを持つグラフなど）のような大きなグラフを適切に処理するアルゴリズムを記述する必要があるということです。 残念なことに、何らかの理由で著者はこの事実を考慮せず、テストプラットフォームには合計50 MBの2つのCPU（最大17スケール<= 50 MBのグラフ）が含まれていたため、競合全体がキャッシュでうまく機能するアルゴリズムを書くことになりました。 受け入れ可能な結果を​​示したのは参加者の1人だけでした-Vadim Zaitsevは、スケールのグラフ22で2つのCPUでかなり高い平均値を受け取りました。 しかし、会議中に判明したように、この参加者はかなり長い間MSTタスクに従事していました。 他の実装されたアルゴリズムの大きなグラフの処理速度は大きくない可能性が高く、コンテストWebサイトで公開されているそれらの数値（さらに悪いことに）とは大きく異なる可能性があります。 また、グラフ構造が非常に異なるという事実、および算術平均も完全に明確ではないため、生産性の平均値を突然考慮する必要がある理由にも注意を払う価値があります。 処理されたグラフのサイズも考慮されませんでした。 提供されたシステムのもう1つの不快な「機能」（2x Intel Xeon E5-2690およびNVidia Tesla K20xを含む）はPCIe 3.0で動作していません（ただし、GPUでサポートされ、サーバーボードに存在します）。 その結果、PCIe 2.0の速度はほぼ3倍低いため、Xeon E5よりも高速な（わずかではありますが）2つのプロセッサーを使用することはできませんでした。



グラフ処理はアーキテクチャ上の機能のためにGPUで並列化するのが難しいため、GPUでこのような問題を解決するのは簡単ではないことに注意してください。 そしておそらく、これらのコンテストは、グラフィックプロセッサ用の非構造グリッドを使用して、アルゴリズムを記述する分野の専門家の開発に貢献するはずです。 しかし、今年の結果と前回の結果から判断すると、残念ながら、そのようなタスクでのGPUの使用は非常に限られています。

参照：

[1] en.wikipedia.org/wiki/Sparse_matrix

[2] www.dislab.org/GraphHPC-2014/rmat-siam04.pdf

[3] www.dislab.org/GraphHPC-2015/SSCA2-TechReport.pdf

[4] www.nvidia.ru/object/tesla-supercomputer-workstations-ru.html

[5] www.nvidia.ru/object/geforce-gtx-titan-x-ru.html#pdpContent=2

[6] www.amd.com/ru-ru/products/graphics/workstation/firepro-3d/9100

[7] en.wikipedia.org/wiki/Bor%C5%AFvka 's_algorithm

[8] www.cs.princeton.edu/~rs/AlgsDS07/01UnionFind.pdf

[9] habrahabr.ru/company/epam_systems/blog/247805

[10] on-demand.gputechconf.com/gtc/2013/presentations/S3174-Kepler-Shuffle-Tips-Tricks.pdf

[11] openmp.org/wp

[12] devblogs.nvidia.com/parallelforall/unified-memory-in-cuda-6

[13] stanford.edu/~vibhavv/papers/old/Vibhav09Fast.pdf

[14] ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5678261&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D5678261

[15] link.springer.com/chapter/10.1007%2F978-3-642-31125-3_6