1.電車の上部の棚に乗るのが好きな理由
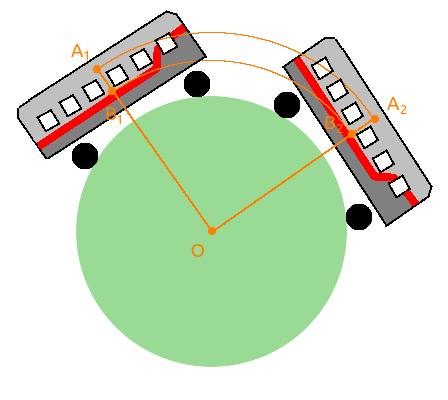
地球がボールであり、私たちがオムスクからモスクワまで円の弧に沿って旅行している場合、下の棚を移動している私の友人は、弧B 1 B 2の長さに等しい経路を移動し、I-弧A 1 Aの長さに等しい経路を移動します2 。
オムスクとモスクワの間は約2500 kmなので、角度A 1 O A 2は約2500/6400 = 0.4 radです。
A 1 A 2 = OA 1・0.4、 B 1 B 2 = OB 1・0.4、および上下フランジ間の距離は約1メートルなので、 A 1 A 2 - B 1 B 2に進みます。 =( OA 1 - OB 1 )・0.4 = 1・0.4 m =同じお金でさらに40センチメートル。
2.友人の三亜の仕事
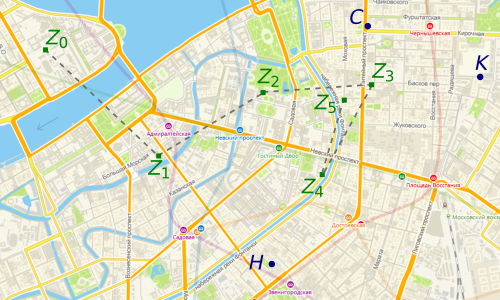
私の友人のアレクサンダーは、同じ夜にナスティア、スヴェタ、カティアという名前の3人の女の子と予約をしました。 彼はフォンタンカ川堤防の90 k5の家の近くのナスティア、リティーニとキロチナヤの交差点のスヴェタ、フォンタナヤ通りの家5のカティアと会うことに同意しました(図の点N 、 C 、 K )。 アレクサンダーはナスティーアと会うために仕事を辞めたが、途中でスヴェタはよりきれいだと思い、彼女と会う場所に行った。 スヴェタへの途中で、彼はカティアとより多くのチャンスがあると思い、彼らが会うことに同意したところに行きました。 しかし、途中で、彼はナスティアがまだ賢いと判断し、ナスティアに向かった。 友人がこのように一晩中歩き続けたら、どこに行きましたか?
解決策
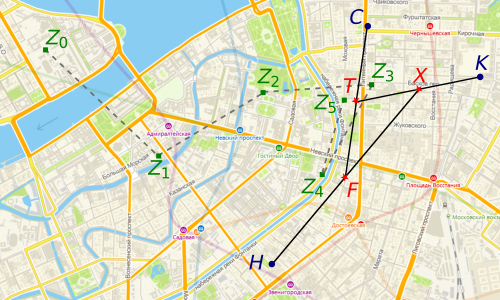
三亜が壁やその他の障害物を歩くことができると仮定します。 サンクトペテルブルクを複雑な平面に置き、 Z 0で機能させます 。 そして、彼が解を変更した点のシーケンスは、 Z 1 =( Z 0 + H )/ 2、 Z 2 =( Z 1 + C )/ 2、 Z 3 =( Z 2 + K )/ 2、 Z 4 =( Z 3 + H )/ 2、...このシーケンスを3つのサブシーケンスに分割します: Z 0 、 Z 3 、 Z 6 、 Z 9 、...; Z 1 、 Z 4 、 Z 7 、 Z 10 、...およびZ 2 、 Z 5 、 Z 8 、 Z 11 、... Let f ( Z )=((( Z + H )/ 2 + C )/ 2 + K ) / 2.次に、最初のサブシーケンスは、 Z 0 、 f ( Z 0 )、 f ( f ( Z 0 ))、 f ( f ( f ( Z 0 )))、...の形式で記述されます。バナッハ不動点定理により、このマップには一意の不動点が存在します。これをXで示します。 さらに、このサブシーケンスはこのポイントに収束します。 他の2つのサブシーケンスについても、同様の理由で、固定点が存在します。これをそれぞれFとTで示します。 これらのポイントはアドレスに対応しています:Nekrasov、26、Rubinstein、5およびBelinsky、11(図を参照)。 最初のアドレスはクロニクルバー、2番目はフィドラーのグリーンバー、3番目はターミナルです。 したがって、アレキサンダーはこれらのバーで一日を過ごし、順番に移動します。
3.どこでもデータを見るための学習
外に出ると、家の柱や壁に、ペアのある紙片がたくさんあります。最初の要素は女性の名前で、2番目の要素は数字のシーケンスです。 以下に例を示します。

これらのペアの2番目の要素にはまったく興味がないので、最初の要素の分布を見てみましょう。
これを行うために、私は8月に一度通りを約6キロ歩いて統計を収集しました。
263件のアナウンスが処理され、TOP-5の名前は次のようになります:アリス、レナ、サビーナ、ダーシャ、ダイアナ:
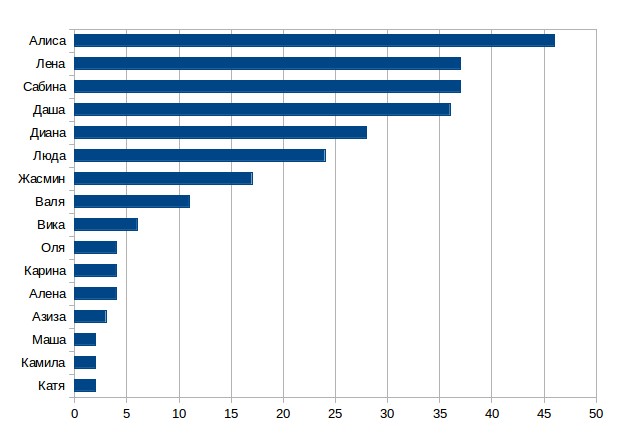
4.友人のコスティアの仕事
友人のコンスタンティンは毎晩7時に仕事を辞め、地下鉄に行きます。 そこで、彼は誤ってブランチと方向を選択し、電車に乗って、1つの駅を通過し、そして再びランダムにブランチと方向を選択し、再び1つの駅を通過し、以下同様に、家に帰ります。 コスティアがレオ・トルストイで働いており、アートの近くに住んでいることを知っています。 m。Belyaevo、仕事の後に家の近くの店でビールを買う場合、ビールを飲む頻度を決めます。
解決策
モスクワメトロは、行列Pを使用してマルコフ連鎖に関連付けることができます(図を参照)。 そして、コスティアが駅に行くので。 m。Belyaevo、この状態Bは吸収されます。
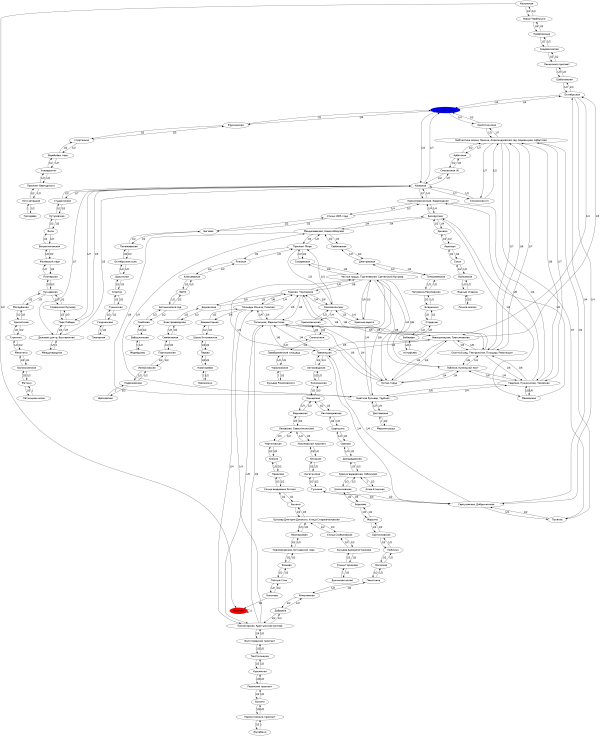
(画像をクリックすると拡大します。)
さらに、1回の運搬に約3分かかると仮定します。 モスクワにいるので、彼らはビールの販売を23:00と(23:00-19:00)/ 3分で止めます。 = 80の場合、80ステップ未満で状態Bになる確率を見つける必要があります。 この確率を見つけるには、行列Pを79の累乗に上げ、カルチャーパークに対応する行とBelyaevoに対応する列の交点の要素を取得する必要があることを理解するのは簡単です。 計算では、望ましい確率が約5.9%であることが示されています(下図を参照)。 そのため、私の友人は17日ごとにビールを飲みます。

5.チプソイド
しばらく前に、Chipsin Pringleが双曲線放物面であるという事実でインターネット上に写真が浮上しました。

彼女を見たとき、私は自分に言いました。 そして、双曲線放物面は支配的な表面であるため、チップシンは直線的なスリットをクロールする必要があります。 そのため、翌日、チップを購入し、段ボール箱のスロットを切り、この実験を行いました。

ルールドサーフェスのもう1つの例は、1枚の双曲面です。 この事実は、ミラクルヨーグルトボトルの助けを借りて確認できます。 ヨーグルトからボトルを取り出し、1枚の双曲面に似たボトルの一部を切り取り、段ボールシートの隙間をもう一度切り、ボトルの一部をスロットに挿入してねじります。

良い一日を!