8250互換USARTのプリスプリッターパラメーターの計算

今夜、プリスプリッターのパラメーターを効率的に計算する方法についてのおとぎ話をお話します。これは通常、USARTポート、特にIntel SoCで使用される8250互換ポートのクロック周波数を設定するために使用されます。





現時点では、分数プリディバイダーを備えたUSARTを使用するIntel SoCのラインが少なくとも2つあります

1. メドフィールド、クローバートレイル、タンジール
2. BayTrail、ブラスウェル

それらの違いは何ですか、少し後で説明します。



以下は、 Fusart -USARTクロック周波数とボー - ボーレートの計算に使用される式です。













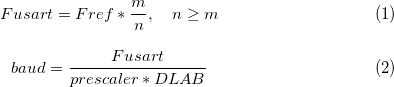
残り

Frefはプリセパレーターの前の周波数、 mは分子、 nはプリセパレーターの有理数の分母、プリスケーラーはフザートを除算した整数、 DLABは8250互換チップで表される16ビット除算器です。



セット全体から、2つの量、つまりFrefとbaudのみがわかります。 プリスケーラーの値は通常16に等しく、一部のチップではそれを変更する可能性がありません（これがIntel SoCラインを互いに区別するものです）

プリスケーラーの計算

本格的なPLLではなく、フラクショナルプリスケーラを使用しているため、 （1）













したがって、すでにプリスケーラ値を計算できます

prescaler = 16 fusart = baud * prescaler if fref < fusart: if fref >= baud: prescaler = fref / baud else: prescaler = 1 fusart = baud * prescaler
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

フザート計算

前の部分は、満たされていない場合にのみ機能します（3） 。 そうしないと、 Fusartは、要求されたかなり低いビットレート（110ボーなど）でFrefに比べて非常に低くなることがあります。



また、通常、分周器の分子と分母は同じ幅（ビット単位）であるため、それらの不一致を制限するとよいでしょう。 これを行うには、 Fusartを可能な限りFrefに持ち込みます。

 fusart <<= int(math.log(fref / fusart, 2))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

なぜこの近似が選択されるのですか？ 問題は、 DLABオーバーフローがあり、それが16ビットしかない場合、2のべき乗を使用すれば、最も単純なビット操作でこれを追跡できるということです。

分母キュー

明らかに、今（1,2）から、単純な割合が続きます











したがって、前除数の有理数の分子と分母を簡単に計算できます。

 divisor = gcd(fref, fusart) n = fref / divisor while n > (2 ** width - 1): divisor <<= 1 n >>= 1 m = fusart / divisor
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、 幅は分子と分母のビット幅です。



それだけです。 Pythonのソースコードは、GitHub Gistで入手できます（既に何度か更新されており、将来更新される可能性があります）。







上記のアルゴリズムは単純で高速ですが、それほど正確ではありませんが、目標を満たしていることに注意してください。