そのため、浮動小数点数の表現に関連する丸めやエラーがないことにすぐに同意します。 整数変数のみを使用します。このため、明らかなトリックに頼ります。 実際には、プログラミングはほとんどなく、多くの数学が必要になります。 この研究では、高校の数学に関する参考資料、または「線形代数と解析幾何学の基礎」[1]の章の1つの段落が使用されました。
まず、タスクのテキストを思い出します。
誰かが突然ドアを開けたとき、冷たいペティアはベッドに横たわっていました。 ペティアは怠けすぎて立ち上がることができず、鏡を見ながら誰が来たのかを確認しました。 入る人の座標はわかっており（重要なポイントと考えることができます）、ピートが鏡に入る人の反射を見ることができるかどうかを調べる必要があります。 ミラーは原点を中心とする円の形をしており、平面ax + by + cz = 0にあります。Petyaも重要なポイントと見なすことができます。 ペティアと見知らぬ人が鏡の平面に横たわることがなく、ペティアが常に鏡の反射面を見ることが保証されています。 画像が鏡の縁に当たると、Petyaは人が入っているのを確認します。 Petyaと入る人の両方が重要なポイントと見なされるため、Petyaは入る人と自分の反射の両方を通して入る人の反射を見ることができます。
まあ、私たちはこのタスクに「額で」アプローチすることはできません;指定されたトピックの解析も、特に「噛む」ことではありません。 したがって、問題を単純化し、2次元空間で解決してから、類推して3次元に移ることを提案します。
もちろん、1次元バージョンでも検討できますが、ミラーは点に変わり、ピーターはミラーの片側にいる場合にのみ入る人を見るため、ほとんど意味がありません。 それらの座標が同じ符号を持っている場合。
問題の図を描いてください：
Petyaが点Sを、見知らぬ人が点Tを、鏡が線分であるとする
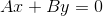
初期データ： R-ミラーの半径、係数AおよびB ;
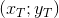-入力された座標;
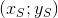-ピーターの座標。
解決アルゴリズムは次のとおりです。
-ポイントTを 通過して 、 PQに垂直な線を引きます。
-この線上で、 PQに対して点Tに対して対称な点T`をマークします。これは、Petyaを見る（または見えない）入った人の画像になります。
-直接のST`を描画します。
-PQとST`の交点を見つけます。
-指定されたポイントがセグメントPQに属しているかどうかを確認します
したがって、点Tを通る直線の方程式は垂直です
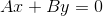次のようになります。
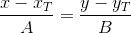または 
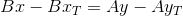
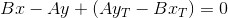
TT`とPQの交点は、連立方程式の解です：
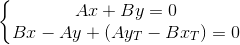
方程式にそれぞれAとBを乗算し、合計します。
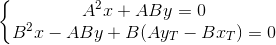
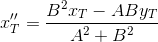
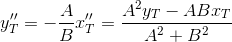
ポイントが見つかりました
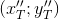点Tの線PQへの投影
ポイントT`の座標を定義します。
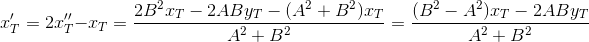
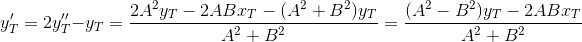
あと2歩。 線ST`の方程式を見つけます。
または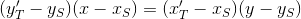 
座標T`の代わりに式を使用します：
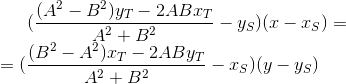
整数計算に任せる-方程式に
：
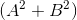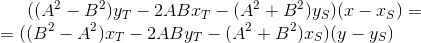
代替品を導入する時が来ました：
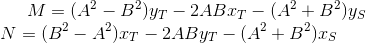
方程式ST`は次の形式を取ります。
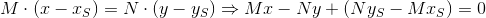
PQとST`の交点は、システムの解決策です。
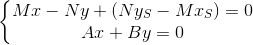
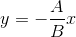
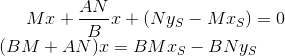
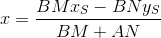
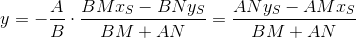
そして最後に、座標の中心から見つかった点までの距離：
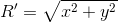
過激派から逃れます。
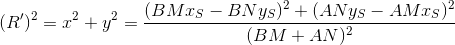
ここで、見つかったR 'が指定されたRを超えない場合、不幸なピーターはまだ入っている見知らぬ人を見ることになります。
比較して
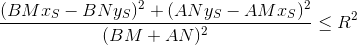不等式の両側に既知の正の値を掛けます（偶数度から）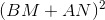 
つまり 表現の真実に興味があります
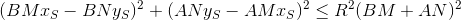
なぜ私はこれをすべてそんなに詳細に書いているのですか？ オリンピアードの参加者がこの問題を解決するためにどれだけの作業を行う必要があるかを示すために、これらの垂直線のすべての式が数学のコースに含まれていませんが、参加者自身が論理的に到達する必要がありますか？ さらに、彼はこのタスクに平均30分割り当てられました。 結局のところ、タスクは実際にはまだ解決されていません。 第一に、3次元空間でも同じことが必要であり、これはさらに面倒であり、第二に、男の子とゲストが鏡の同じ側にいるかどうかはここでは考慮されません...
まあ、私たちは時間的なプレッシャーの危険にさらされていないので、続けます。
「ルッキンググラス」を扱います。
私はそのような解決策を持っています（すぐに頭に浮かびませんでしたが、最初は直接ミラーに関連付けられた座標系に移動することを考えましたが、「ugい」三角関数があります）-ポイントSとTを通して、与えられた
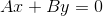。 平行線には、 xおよびyに複数の係数があります。 
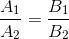、違いは無料会員のみです。 何も発明せず、これらの係数を与えられたAとBに等しくします。
次に、 PQに平行な点Sを通る直線の方程式は次の形式になります。
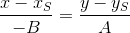または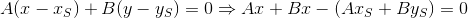 
ここでは、無料会員のサインに応じて
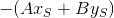線は、指定された線の片側または反対側にあります。
同様にTを通過する行の場合：
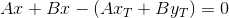
次のことをしましょう：製品の価値を見つける
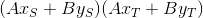ゼロと比較します。ゼロよりも大きい場合、ポイントは線の片側に位置し、それよりも小さい場合は異なり、ペティアは間違いなくゲストを表示しません。 この場合、少なくとも1つのポイントが特定のライン上にあります。
さて、最後に、3次元の世界のプログラムのテキスト、つまり 問題の初期状態の場合：
src
package ru.andrewn; import static java.lang.System.out; public class Program { public static void main(String[] args) { java.util.Scanner sc = new java.util.Scanner(System.in); out.println(" r:"); int R = sc.nextInt(); out.println(" a, b c:"); int A = sc.nextInt(); int B = sc.nextInt(); int C = sc.nextInt(); out.println(" (x, y z):"); int xx = sc.nextInt(); int yy = sc.nextInt(); int zz = sc.nextInt(); out.println(" (x0, y0 z0):"); int x0 = sc.nextInt(); int y0 = sc.nextInt(); int z0 = sc.nextInt(); if ( (A*x0+B*y0+C*z0)*(A*xx+B*yy+C*zz) >= 0 ) { int M = (B*B+C*CA*A)*x0-2*A*B*y0-2*A*C*z0-(A*A+B*B+C*C)*xx; int N = (A*A+C*CB*B)*y0-2*A*B*x0-2*B*C*z0-(A*A+B*B+C*C)*yy; int K = (A*A+B*BC*C)*z0-2*A*C*x0-2*B*C*y0-(A*A+B*B+C*C)*zz; if ( (A*M+B*N+C*K)*(A*M+B*N+C*K)*R*R >= ((B*N+C*K)*xx-B*M*yy-C*M*zz)*((B*N+C*K)*xx-B*M*yy-C*M*zz) + ((A*M+C*K)*yy-A*N*xx-C*N*zz)*((A*M+C*K)*yy-A*N*xx-C*N*zz) + ((A*M+B*N)*zz-A*K*xx-B*K*yy)*((A*M+B*N)*zz-A*K*xx-B*K*yy)) out.println(" "); else out.println(" "); } else out.println(" "); sc.close(); } }
コードが曲がってすみません、私はプログラマーとは程遠いです。
希望する人がいれば、3次元の世界に数学的な計算を添付することもできます。
まとめ
この出版物の教訓は、それでもオリンピックのタスクのコンパイラーは、問題の解決がいかに骨の折れるものであるか、割り当てられた時間内に成功するために必要な知識をより注意深くチェックするべきであるということです。
文学
1.コルニエンコ、V.S。 数学の参考資料：独学のためのマニュアル[電子リソース] / V.S. コルニエンコ; ヴォルゴグラ 状態 S.-kh. Acad。 ヴォルゴグラード、2010.284秒