パート1.実際のデータ
より興味深いものにするために、ストーリーは例に基づいて構築されており、データとして(この記事および以下の記事で)ここから直接Habrから統計を取得しようとします。 つまり、1週間前にHabréに関する最初の記事を書きました (Mathcad Expressについて、すべてを数えます)。 そして今、10日間のビューに関する統計がソースデータとして提供されています。 グラフでは、これは一連のビュー、青い線です。 データの2行目(Regs、係数100)は、読み取り(Mathcad Prime配布キットの登録とダウンロード)後に特定のアクションを実行したリーダーの数を示しています。
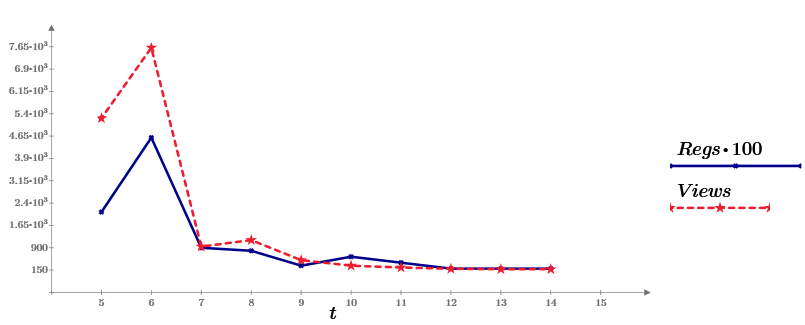
たまたま、私は、記事を表示するための統計(Habrから)に加えて、Mathcadのダウンロードの統計にアクセスできました(記事の本文内で提供したリンクを介して)。 したがって、 コンバージョンなどのインターネットマーケティングの概念に対処するためのすべてが揃っています。 コンバージョンは通常、購入や登録などを完了したサイト訪問者の数の比率と呼ばれます。 訪問者の総数に。 たとえば、公開の初日、私の記事は5,000回閲覧され、20回のダウンロードがありました。 コンバージョンは0.4%でした。
すべての写真はMathcad Expressのスクリーンショットです(計算自体はここで取得し 、繰り返し、必要に応じて変更して使用できます)。 手で初期データ(3つのベクトル)を入力しました。

変換の計算(%)は次のとおりです。「インスタント」(毎日)および「平均」(10日間)。 変換値が時間の経過とともに少し「浮動」すること(最初の日の0.4%から最近の準定常的な1%まで)は、それ自体で議論する価値があります(ランダムプロセスと相関時間については次の記事に延期します) )
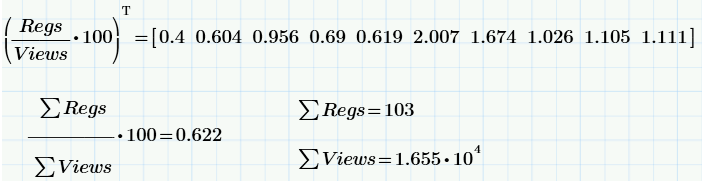
ターゲットアクション(ダウンロード)の数がビューの数に依存するという明らかな事実は、Regs(ビュー)チャートによって明確に示されます。 ビューの数とダウンロードの数はランダムですが、それでも(ほぼ)線形の関係によって関係していることがわかります。
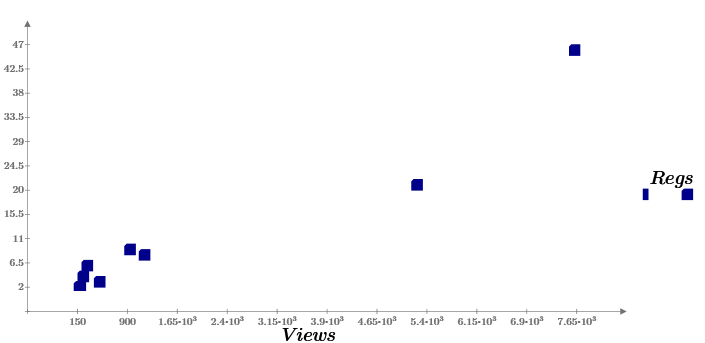
少し「学校」の統計:2つのサンプルビューとRegsの平均値、分散、相関係数の計算(定義による)。
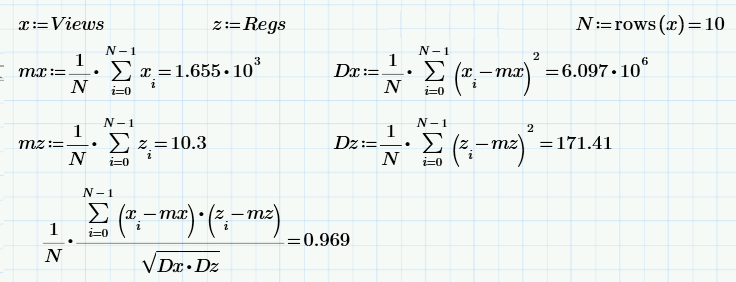
最後の式は、相関係数の計算です。これは、2つの確率変数がどの程度依存しているかの尺度(より正確には、線形依存の尺度)です。 相関係数のサンプル値は0.97です。 これは非常に大きな問題です(偶然にも、問題の声明から驚くことではありません)。
最後に、数学的回帰の問題を解決します。一般的な場合、特定の関数f(x)によるデータサンプリング(x、z)の近似で、特定の方法で誤差f(x)-zのセットを最小化します。 f(x)= A * x + Bの場合、最も単純で最も一般的に使用される回帰タイプは線形です。 係数AとBは通常、二乗誤差の合計を最小化する条件から計算されるため、別の線形回帰は最小二乗法と呼ばれます。
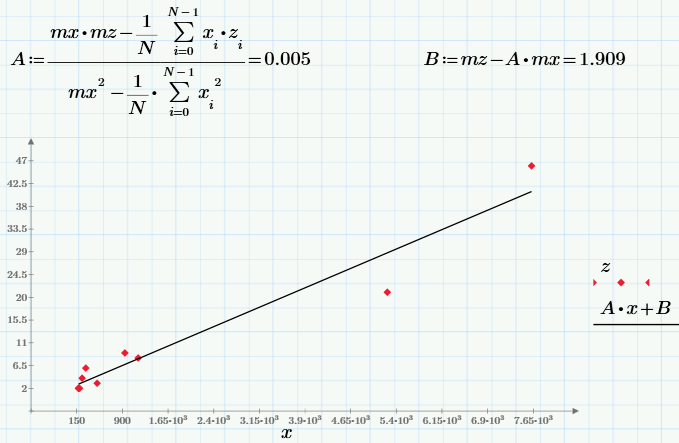
ところで、最小二乗法(二乗誤差の合計を最小化する)は、回帰を構築するための唯一の可能なオプションではありません。 たとえば、中央値と中央値の線形回帰が使用されることがあります。
最後に、問題で回帰が必要な理由について。 ダウンロードのビューへの依存性の線形性を考慮すると、係数Aは変換を特徴付けるだけです。 それから判断すると、コンバージョンは0.005 = 0.5%です。つまり、たとえばマーケティング目標がある場合-ダウンロード数100に到達するために、線形回帰モデルに基づいて、サイトに100 / 0.005を「アップロード」する必要があります= 2万ビュー。
パート2.モンテカルロモデリング
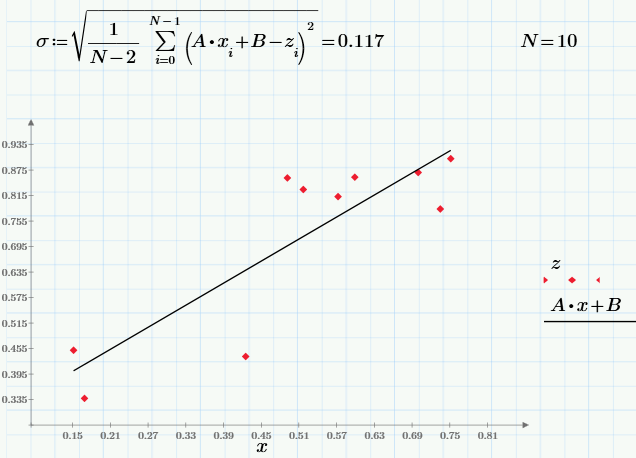
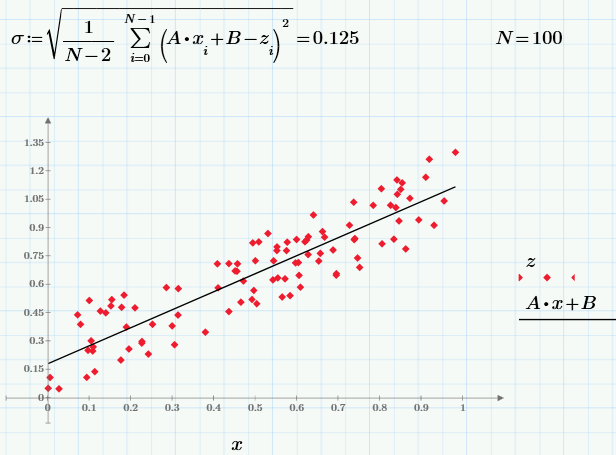
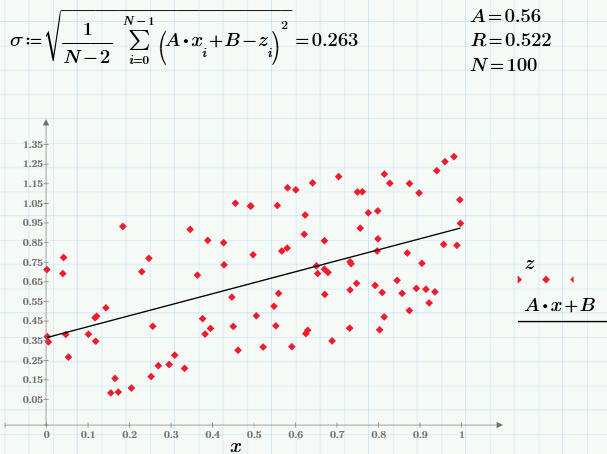
最後の部分では、実験中に取得したランダムデータを操作しましたが、結論として、疑似乱数センサーを使用して同じ計算を繰り返します。 モンテカルロ法では、特定の相関関係を持つ乱数を作成することがしばしば必要です。 最初に、3つの擬似ランダム配列を生成します。xとyは独立しており、zはxに依存しています(相関係数rの「一般的な」値を使用)。
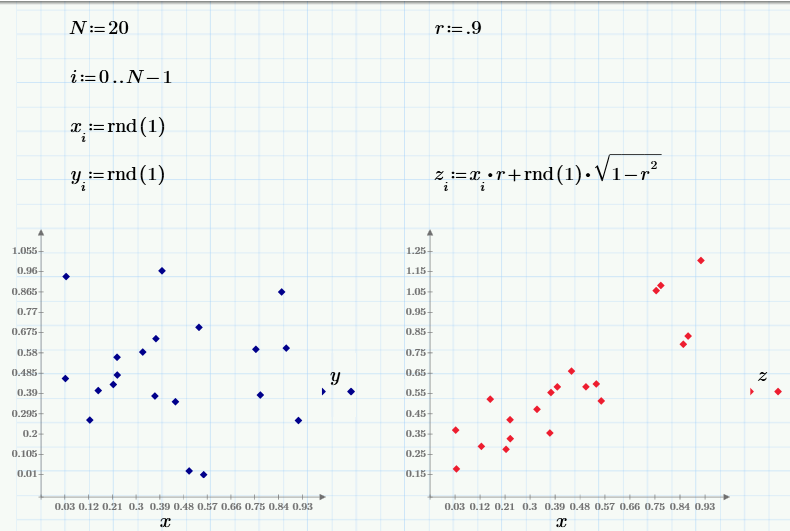
左側のグラフは、xとyの無相関のランダム値の依存関係を示し、右側のグラフは、相関のあるzとxの依存関係を示しています。
前のセクションと同じ式を使用して、サンプルx、y、およびzの統計特性(相関係数のサンプル値を含む)を取得します。
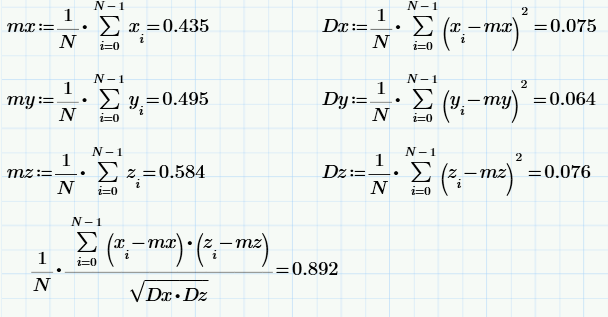
最後に、最小二乗法の式に従って、線形回帰z = A * x + Bを作成します。
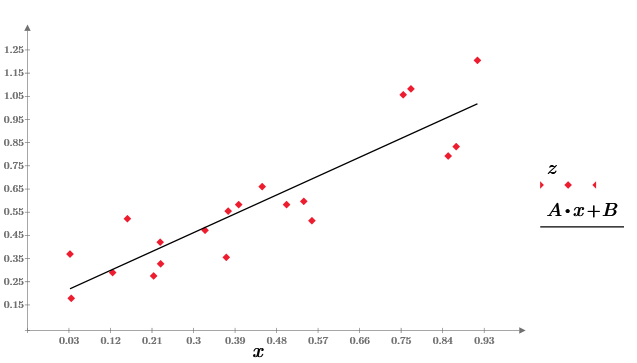
興味のある読者には、パラメータrを実験して、その変更が依存関係z(x)にどのように影響するかを見てもらいます。 サンプルサイズNを変更して、統計的特性を計算した結果に従います。
参照:
- ビデオコース「機械学習」 (Yandex SHAD)
- ガレス・ジェームズ、ダニエラ・ウィッテン、トレバー・ヘイスティ、ロバート・ティブシラニ。 Rの統計学習の概要(PDF)
- トレバー・ヘイスティー、ロバート・ティブシラニ、ジェローム・フリードマン。 統計学習の要素(PDF)