
翻訳者のメモ :ロシア語を話す頭/尾を混乱させないように、頭/尾のコインの側面の元の指定を表/裏に置き換えました。 上の図では、左側が表面(頭)、右側が裏面(尾)です。
救いは不可能ですか?
これは、死刑判決を受けた囚人に関する典型的なパズルの1つであり、看守に精神的な能力を証明した場合にのみ保存できます。 あなたとあなたの友人は投獄されました。 あなたの看守はあなたにテストを提供します。 それに従うと、あなたの両方が解放されます。
ルール:
- 看守は別のセルに連れて行ってくれます。 部屋にはチェス盤と64個のコインが入った缶が入っています。
- 看守は、コインを1枚ずつ取り、ボードの各マスに置きます。 彼はコインをarbitrarily意的に配置します -いくつかは逆さまになり、いくつかは逆になります(またはすべてが表向き、または逆になります、あなたは知らない、すべてが看守の裁量にあります)。 コインを配置するプロセスに介入しようとすると、即座に死に至ります。 何らかの方法で看守を強制、助言、または説得しようとすると、即時に死亡します。 あなただけが見ることができます。
- すべてのコインが配置されると、看守はセルの1つを指し、「これ!」と言います。示されたセル-「魔法」は自由への鍵です。
- 看守は、ボード上のコインを1枚反転させることができます。 1つだけですが、お好みのコインにすることができます。 これは、看守のレイアウトで行うことができる唯一の変更です。
- その後、部屋から連れ出されます。 友達にメッセージやヒントを残そうとすると...はい、あなたはそれを推測しました、即死!
- 看守はあなたの友人を部屋に連れて行きます。
- 友人はボードを調べて(タッチすることは禁じられています)、彼の意見では「魔法の」セルがどこにあるかを判断する必要があります。
- 彼の試みは1つだけです。 コインの位置に基づいて、彼はセルを指して、「これ!」と言わなければなりません。
- 彼が正しく指示した場合、あなたは両方の恩赦とすぐに解放されます。 それが間違っている場合、あなたの両方が実行されます。
- 看守は、これらの規則を事前に両方に説明し、戦略を策定するための時間を与えます。
戦略を立てることは可能ですか?
一見、この問題は解決できません。 私たちは看守に影響を与えることはできません。コインのレイアウトはどのようなものでもかまいません。また、監獄がどのセルを指すのかわかりません(実際、彼は自分がどのセルを選択するかわからないかもしれません)。
彼が指すことができる64のセル。 2 6の可能な答え。 セルを正確に識別するには、6ビットの情報が必要です。 コインを投げると、これはほんの少しの情報です。 ボードの状態を「前」に伝えることができないため、友人には、どのコインが逆さまになっていたかを示す機会がありません。 友人が部屋に入って、表側63と裏1を見ると、裏はあなたが裏返したコインだけか、裏表62と裏2を持っているボードがあり、裏を1枚裏返したことを彼は知ることができません!
1枚のコインを裏返すことで6ビットの情報を送信することは可能ですか?
コインのレイアウトや「魔法の」セルの位置に関係なく、100%の確率で保存できる戦略があります。 このソリューションは、詐欺やトリックを意味するものではなく、純粋に数学的なものです。
開始する
実際、私たちはあなたとあなたの友人の間で送信された1ビット以上の情報を持っているので、問題は解決できます。 残りのコインの場所には情報が保存されており、それを使用できます。 実際、コインレイアウトには十分な(6つの)制御ビットがあり、ボード上の任意のセルを識別できます。
2つのセル
セルが2つしかないボードがあるとします。 コインの場所には4つのオプションがあります(A-表面、P-裏面):PP、AA、RA、AR。

看守は、最初のセルと2番目のセルとして「魔法」を選択できます。
事前に、1つのルールに同意します。看守が最初のセル(白)を指している場合、表側が最初のセルにあることを確認する必要があります。 可能なオプション:
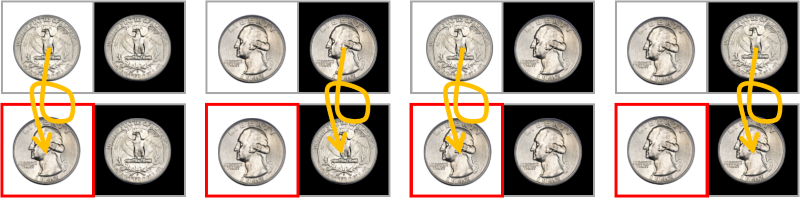
レイアウトがPPの場合、AAの場合、最初のコインを表側で裏返すことができます-最初のコインはすでに表側で裏返されているため、2番目のコインを裏返します(ルールに従って、これは何も変更しませんが、コインを裏返す必要があります)。
上記のすべてのケースで、表面は最初のセルにありました。 ルールによれば、これは看守が最初のセルを選択したことを意味します。
同様に、看守が2番目のセルを指す場合は、最初のセルに表側が存在しないようにします。 これは、「魔法の」セルが最初ではないという私の友人への手がかりです。

すべての場合において、最初のセルには表面はありません。 ルールによれば、これは看守が2番目のセルを選択したことを意味します。
問題は解決しました!
誘導
数学者(および一部のプログラマー)は、問題の解決が可能であることを証明するために必要なのはこれだけであることを教えてくれます。 2つのセルを使用して1ビットの情報をエンコードできれば、数学的帰納法を使用して、4セルに2ビット、64セルに3 in 8 ... 6ビットをエンコードできることを確認できます。
バイナリ表現
バイナリ表現で0(左上)から63(右下)までのセルをマークすると、各セルがどのネストセットの一部であるかを表示できます。
元の記事には、ボードのインタラクティブな画像が含まれています。 左下隅の数字は、セル番号をバイナリ表記で表示します。 各数字は、セルが属するセットを表します。 任意の位置のユニットは、セルがセットの半分にあり、もう一方にゼロがあることを示します。 定義上、各セルは一意であり、個々のビットのセットを持っています。
パリティ
上記の簡単な例のように2つのセルを使用する代わりに、ボードを2つのセットのさまざまな組み合わせに分割します。 単一のセルと同じラベル付けルールをこれらの2つの領域/セットに適用します-最初の領域または2番目の領域に「魔法の」セルがあるかどうかを示します。
リージョンはセルのコレクションであるため、リージョン内のすべてのコインを単純に表向きに回転させることはできません。 代わりに、コインを1枚めくります。 領域内の表面の数を計算することができます-それらの数が奇数の場合、偶数の場合は1とします-ゼロ。 領域内の1枚のコインを裏返すと、表側の数が奇数から偶数に変わり、その逆も同様です(任意の数に単位を加算/減算すると、その偶数/奇数が反転します)。
これがパリティの概念です。 1ビットを加算または減算することにより、ある状態から別の状態に切り替えることは、コンピューターで広く使用されています。
リージョンのパリティを変更するには、1つのコインをフリップするだけです。
2のべき乗のマスクを使用して、ボードをいくつかの方法で領域に分割できます。 以下は、セル番号のビットの状態(2のべき乗)に基づいてボードを分割するさまざまな方法です。 これらのフィルターの組み合わせにより、任意の/すべてのビットのパリティを変更するために裏返すことができる1つのセルを定義できます。

2 0は 、000001、2 1-000010 ... 2 5-100000の論理「AND」(AND)と同等です。
定義上、各セルには一意のビットセットがあります。 これらのフィルターの任意の組み合わせのパリティを変更するためにコインを1枚反転できます。
jailerによって作成されたレイアウトには、独自の(自然な)パリティがあります。 コインはランダムに配置され、各領域のパリティ(表面の数)を計算できます。 これらのパリティビットの組み合わせにより、ランダムな6ビット数が得られます。
「魔法の」セルを識別するために必要なのは6ビットだけで、パリティを使用してエンコードできます。 コインを1枚ひっくり返すことができることはわかっています。これにより、数の1ビットまたは数ビットが変更されます。 必要なのは適切なコインを見つけることです。それを裏返すと、パリティビットの組み合わせが変更され、必要な数(「マジック」セルの数のバイナリ表記)が得られます。
すべて一緒に
ここで、元の記事のインタラクティブモデルに読者を再度送ります。

左のボードでは、「魔法の」セルの場所を選択できます。 右下には選択されたセルの番号(ターゲット= ...)、左にはそのバイナリ表現があります。
右側のボードは、コインのレイアウトを示しています。 表面のみが表示され(わかりやすくするため)、裏面は空のセルで示されます。 「ランダム」ボタンは、新しいランダムなコインのセットでボードを埋めます。 「クリア」ボタンは、すべてのコインを反転させます。
右側のボードの下で、左側の灰色はボード自体のパリティを示し、右側の緑色は裏返すコインの数を示します。 左側の独自のパリティの下に、同じ番号がバイナリ形式で書き込まれます。
これらの値はどこから来たのですか?
左のボードの下で番号がどこから来たかはすでにわかっています。 これは、セルの単なるバイナリの説明です。数字の各ビットは、上記の2つのパワーフィルターにこのコインが存在するかどうかを示します。
右側のボードの下にある灰色の数字は、ボード自体のパリティを示しています。 各フィルターについて、この領域にある偶数または奇数の表面を見つけます。 任意の数字の単位は、領域の表面が奇数であることを示します。
緑色の数字は、ボードのパリティが「マジック」セルの目的の数と一致するように、状態を変更する(コインをフリップする)セルの番号を示します。 ボード自体のパリティと目的の値に対して「OR」(XOR)を除外するビット演算を実行することで計算されます。
排他的OR
XOR演算子は、プログラミングで広く使用されています。 いくつかの興味深い特性があります。 排他的な「OR」が同じ値で2回適用されると、元の状態に戻ります。
(A XOR B)XOR B = A
また、数値と完全なビットセット(1つのユニットのみで構成される数値)にXORを適用すると、元の数値のすべてのビットが反転します。 XORを数値といくつかの(セット)ビットのセットに適用すると、元の数値のこれらのビットが反転し、残りの状態が保存されます。
そのため、XOR演算子を使用してコインの位置を計算しました。 パリティビットごとに、既に正しい値が含まれているかどうかに関係なく、保存する(XOR c 0)か、切り替えるか(XOR c 1)します。
例:
「マジック」セルの番号が101001(41)で、ボードのパリティが010101の場合、セル111100(60)でコインをフリップする必要があります。

XORを使用して、独自のパリティをすばやく計算することもできます。 これを行うには、ボード全体を一周し、表面のセルの各値(シリアル番号)でこの操作を実行します。