私たちの周りの統計
統計とデータ分析は、現代のほとんどすべての知識分野に浸透しています。 現代の生物学、数学、コンピューターサイエンスの間に線を引くことはますます難しくなっています。 経済調査と回帰分析はほとんど分離不可能です。 正規分布を確認する既知の方法の1つは、コルモゴロフ-スミルノフ基準です。 数学言語学の発展に多大な貢献をしたのはコルモゴロフであることをご存知ですか?
サンクトペテルブルク州立大学の心理学部の学生として、私は認知心理学に興味を持ちました。 ところで、インマヌエル・カントは心理学を科学とは考えていませんでした。なぜなら、彼はその中で数学的な方法を使用する可能性を認識していなかったからです。 私の現在の研究は精神プロセスのモデリングに専念しており、計算モデルやコネクティビストモデルなどの現代の認知心理学の分野が彼の態度を和らげることを願っています!
もちろん、統計は科学研究所の境界をはるかに超えて適用されます:広告、マーケティング、ビジネス、医学、教育など。 しかし、最も興味深いことに、データ分析の基本的な知識は日常生活で非常に役立ちます。 たとえば、算術平均の概念はみなさんご存知だと思います。 平均値は、収入、失業など、さまざまな社会経済指標を議論する際にメディアで非常に頻繁に使用されます。 2005年、英国のメディアは、人口の平均所得レベルは前年に比べて増加しただけでなく、0.2%減少したと書いています。 「1990年以来初めて人口の収入が減少した」という見出しがちらつく。 一部の政治家は、現在の政府を批判するためにもこの事実を使用しています。 ただし、属性が対称分布(豊富なものと貧しいものが多い)がある場合、算術平均は良い指標であることを理解することが重要です。 実際の収入の分配は次のとおりです。
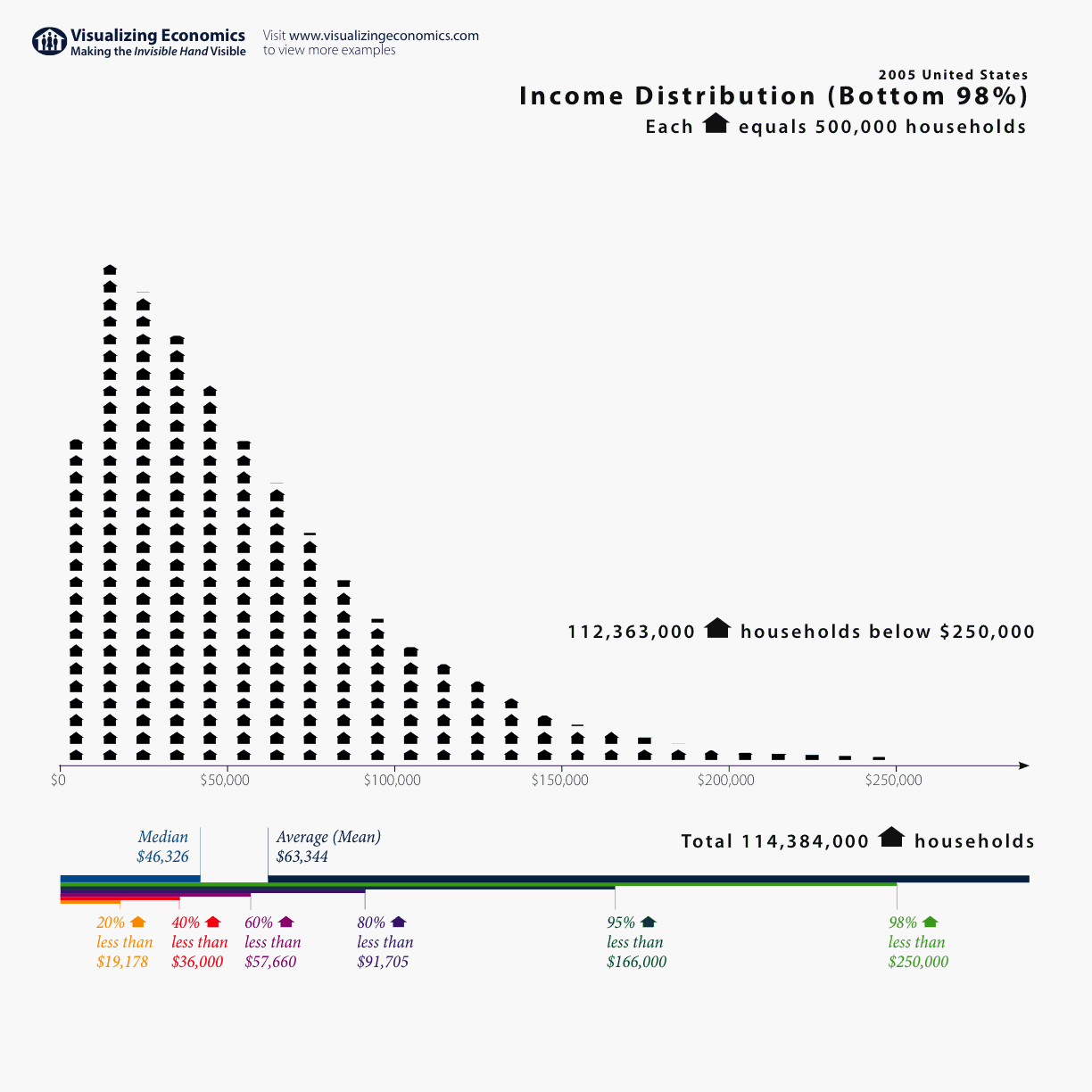
この分布には顕著な非対称性があります。非常に裕福な人々は、中流階級よりも著しく少ないです。 これは、この場合、億万長者の一人の破産がこの指標に大きな影響を及ぼす可能性があるという事実につながります。 中央値を使用してこのようなデータを記述する方がはるかに有益です。 中央値は、収入分布の真ん中にある給与値です(すべての観測値の50%は中央値より小さく、50%多い)。 そして、驚くべきことに、英国の2005年の平均収入とは対照的に、平均収入は増加し続けました。 したがって、さまざまなタイプの分布と中心傾向のさまざまな測定値(平均と中央値)について知っている場合、例で説明されているようなケースで誤解を招くことはそれほど容易ではありません。
統計分析ブラックボックス
すでにわかっているように、あなたが何をしようとしても、「あなたの地域の数学的統計」コースに出会う確率は徐々に近づいています。 ただし、統計の導入に関する授業は、技術を持たない学部の学生の間で喜びをもたらさないことがよくあります。 数回のレッスンの後、たとえば相関などの基本概念は次のようになります。
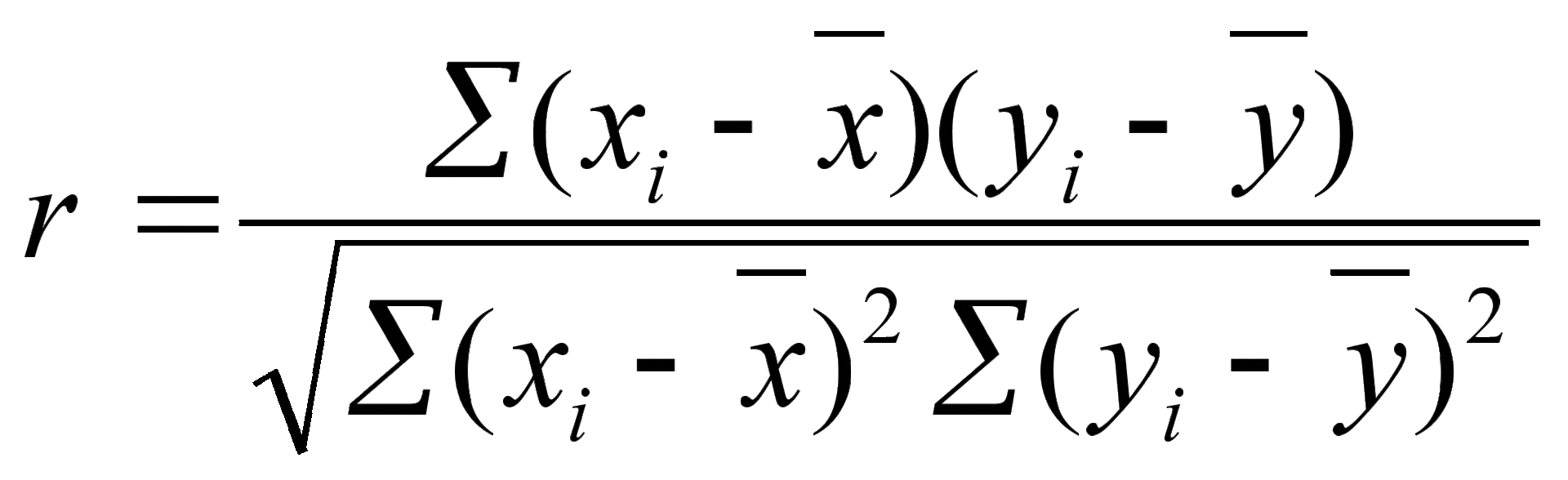
そして、これらの和と平方根の起源を完全に理解するために必死になって、学生は次のように統計を知覚し始めることができます。「r> 0ならば正の接続、0未満なら負の接続」。 「有意水準pが0.05未満である場合、それは良好です。0.05から0.1である場合、あまり良くありませんが、0.1を超える場合、それは悪いです。」 学生が試験の準備をするのを助けて、私はそのような呪文に何度も出くわしました! また、もちろん、これらのすべての指標を手動で計算する人はいません。たとえば、 SPSSを使用すると、「2つの平均を比較する方法」という2番目の段階的な指示を1秒間にgoogleできます
- こちらをクリックしてください
- ここから削除/チェックマーク
- p <0.05->利益
統計分析はブラックボックスに似始めます。データは入力、出力は主な結果とすべてのiにドットを付けるp値(p値)の表です。
実際にp値とは何のことですか?
血まみれのコンピューターゲームへの依存と実生活での攻撃性との間に関係があるかどうかを調べることにしたとします。 このために、それぞれ100人の小学生の2つのグループがランダムに形成されました(グループ1-シューティングゲームのファン、グループ2-コンピューターゲームをプレイしない)。 攻撃的な行為の指標として、例えば、仲間との戦いの数。 私たちの想像上の研究では、学校のゲーマーのグループが本当に非常に頻繁に同志と対立することが判明しました。 しかし、違いがどの程度統計的に有意であるかをどのように知ることができますか? たぶん、偶然に観測された違いが得られたのでしょうか? これらの質問に答えるために、有意性のpレベルの値(p値)が使用されます。これは、一般的な母集団に実際に差がない場合、そのようなまたはより顕著な差を得る確率です。 言い換えれば、実際にはコンピューターゲームが攻撃性に影響を与えない限り、グループ間でこのような差またはさらに強い差が生じる可能性があります。 それほど複雑に聞こえません。 ただし、非常に頻繁に誤って解釈されるのはこの統計指標です。
そして今、p値に関するいくつかの例

そのため、標準的なt検定(またはノンパラメトリックChi基準-この状況でより適切な二乗)を使用して、攻撃性の観点から学童の2つのグループを互いに比較し、切望されている有意水準のpレベルが0.05(たとえば、0.04)未満であることがわかりました。 しかし、結果の有意性のp値は実際に何を教えてくれるのでしょうか? したがって、p値がそのような差またはより顕著な差を得る確率である場合、一般集団に実際に差がない場合、正しい意見は次のようになります。
- コンピューターゲームは攻撃的な行動の原因であり、確率は96%です。
- 攻撃性とコンピューターゲームが無関係である確率は0.04です。
- 0.05より大きいpレベルの有意性が得られた場合、これは攻撃性とコンピューターゲームがまったく関連していないことを意味します。
- このような違いを誤って取得する確率は0.04です。
- すべてのステートメントが間違っています。
5番目のオプションを選択した場合、絶対に正しいです! しかし、多くの研究が示すように、データ分析の経験が豊富な人でさえ、p値を誤って解釈することがよくあります(たとえば、 この興味深い記事を参照できます)。
すべての答えを順番に見てみましょう。
- 最初のステートメントは相関エラーの例です。2つの変数間の重要な関係の事実は、原因と結果については何も伝えません。 たぶん、コンピューターゲームをプレイすることに時間を費やすことを好むのは、より攻撃的な人々であり、コンピューターゲームは人々をより攻撃的にしません。
- これはより興味深い声明です。 問題は、最初にこれを受け入れることです。実際、違いはありません。 そして、これを事実として念頭に置いて、p値を計算します。 したがって、正しい解釈:「攻撃性とコンピューターゲームが何らかの方法で接続されていないと仮定する場合、そのようなまたはさらに顕著な違いを得る確率は0.04でした。」
- しかし、取るに足らない違いを得るとどうなるでしょうか? これは、調査された変数間に関係がないことを意味しますか? いいえ、これは違いがある可能性があることを意味するだけですが、私たちの結果ではそれらを検出することはできませんでした。
- これは、p値の定義自体に直接関連しています。 0.04は、そのような、またはさらに極端な差異を得る確率です。 私たちの実験のように正確にそのような違いを得る確率を評価することは基本的に不可能です!
これらの落とし穴は、このようなインジケーターをp値として解釈する際に隠される可能性があります。 したがって、基本的な統計指標の分析および計算の方法の基礎となるメカニズムを理解することは非常に重要です。
Statistics Essentialsオンラインコース:シンプルな言語による複雑な数式
現在、私はサンクトペテルブルク州立大学心理学部で論文を書いており、バイオインフォマティクス研究所で生物学者に統計を教えています。 講義コースと私自身の研究経験に基づいて、必ずしもバイオインフォマティクスや生物学者でなくても、誰でもロシア語で統計を紹介するオンラインコースを作成するというアイデアが浮上しました。
データ分析と統計に関する優れたオンラインコースは多数あります(たとえば、 such 、 such 、 またはsuch )が、ほとんどすべてが英語です。 このコースが、統計の基礎に精通している人に役立つことを願っています。 その中で、データ分析の基本的な考え方と方法を最もアクセスしやすい形式で分析し、仮説の統計的検定と結果の解釈の考え方に特に注意を払っています。 例には、バイオインフォマティクスから社会学まで、さまざまな分野のタスクが含まれます。 コースは無料で、すべての教材は卒業後2月15日から開いています。
便利な資料
統計の概要に関する有用なコースや資料を知っている場合は、コメントを共有してください!