ロックフリーのデータ構造。 並行マップ：再ハッシュ、再構築なし

C ++ 2015ロシアの軌跡をさらに追ってみましょう。

前回の記事では、ロックフリーの順序付きリストのアルゴリズムを調べ、それに基づいて最も単純なロックフリーハッシュマップを作成しました。 このハッシュマップには欠点があります。ハッシュテーブルのサイズは一定であり、コンテナ内の要素数を増やすプロセスでは変更できません。 事前に必要なコンテナ量をおおよそ表す場合、これは問題ではありません。 そうでない場合は？



ハッシュテーブルのサイズを増やすだけでなく減らす手順（再ハッシュ）は非常に難しい



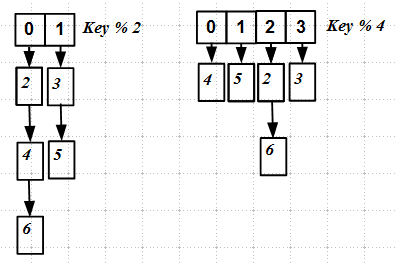
この単純な図からもわかるように、リヘイズ中に、キーは新しいハッシュテーブルの他のスロットに再配布されます-ハッシュマップは完全に再構築されます。 アトミックに、またはロックなしで実装することは非常に困難です。

Nir ShavitはOri Shalevとともに何度も言及しましたが、反対側から問題を見ました：まあ、キーを新しいスロット（バケット）にアトミックに再配布することはできませんが、既存のスロットに新しいバケットを挿入するだけでよい場合があります。それを2つの部分に分割しますか？ このアイデアは、2003年に開発した分割順序リストアルゴリズムの基礎を形成しました。

分割リスト

新しいバケットを取り込んで挿入することはできません -上の図を参照してください：キーを再ハッシュすることがバケット間で再配布される場合、それらの位置を変更しないでおく必要があります。 次のような奇妙なものが必要です。



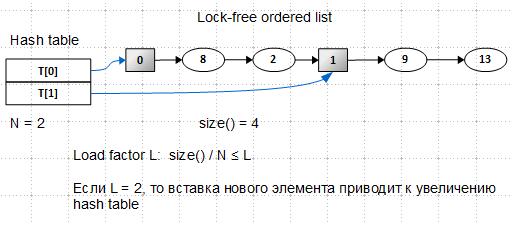
これは、すでに確認したロックフリーの順序付きリストに基づいています。 2つのタイプのノードが登場しました：通常のノード（楕円）と補助（センチネル）ノード（正方形）。 補助ノードはバケット開始ラベルの役割を果たし、削除されることはありません。 ハッシュテーブルには、これらの補助ノードへのポインタがあります。

この写真を見て、あなたは尋ねることができます：リストは順序付けられていますが、これは見えません-キーはランダムに配置されています、問題は何ですか？ 回答：リストは順序付けられていますが、少し後で順序の基準を発明します。

したがって、補助ノードを指す2つのスロットを持つハッシュテーブルがあります。 リストのサイズは4（要素の数をカウントするときに補助ノードは考慮されません）、負荷係数は2です（これは私の自発的な決定です）。 キー10の新しい要素を挿入します。



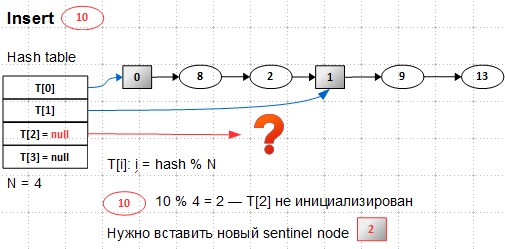
新しい要素を挿入しようとすると、リストがいっぱいであることがわかります。要素の数は5になり、bucket'ovの数は2、5 5/2 > load factor



、-テーブルT[]



を展開する必要があります。 何らかの方法で拡張したとします-4つのバケットがあり、最初の2つは初期化され、最後の2つは初期化されていません。 新しい要素10は、まだ初期化されていないバケット2（ 10 mod 4 = 2



、以降、明確にするためにhash(key) == key



）に入る必要があります。 そのため、最初に補助要素2を挿入する必要があります。つまり、既存のバケットを分割する必要があります。 まず、 親と呼ばれるこの既存のバケットを見つける必要があります。



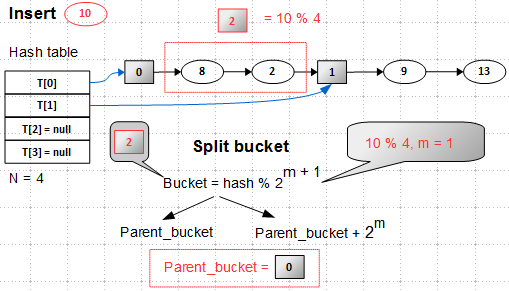
バケットを分割することは、おそらくアルゴリズムの最も細い点です。 親バケットはまだ認識されていませんが、ハッシュテーブルの前半にある必要があります。つまり、この場合はバケット0または1です。

バケットはhash(key) mod 2**(m+1)



で、 2**(m+1)



はハッシュテーブルのサイズです。 新しいバケットは親を分割します。つまり、親バケットの要素を2つのキャンプに分割します。1つは親バケットにあり、もう1つはparent_bucket + 2**m



ます。 したがって、新しいバケット2の場合、親はバケット0です。

C ++では、親バケットを計算する手順は非常に簡単に見えます。

  size_t parent_bucket( size_t nBucket ) { assert( nBucket > 0 ); return nBucket & ~( 1 << MSB( nBucket ) ); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、 MSB



は最上位ビット-最上位シングルビットの数です。



したがって、要素10を挿入するには、まず新しいバケット2を作成し、バケット0に貼り付ける必要があります。 順序付きリスト用の既成のアルゴリズムがあるため、分割順序付きリストの順序を決定するときがきました。

これまでに行ったすべての操作は、2の累乗を法とする算術演算に基づいていることに注意してください。 キーのバイナリ表現を見てみましょう。



そして今-注意：キーのバイナリ値を右から左に読むと、ソートされたリストを取得します：



このような逆ハッシュ値をシャーと呼びます。

したがって、リストをソートするための基準は、キーの反転された（右から左に読み取られる）ハッシュ値に基づいています。



おもしろいことがわかります。bucket'yはキーのハッシュ値によって計算され、逆ハッシュ値でソートされます。 主なことは混乱しないことです。

しかし、それだけではありません。 もう一度図を見ると、キー2のノードが既にリストにあり、通常のノードであり、同じキーを持つ補助ノードを挿入する必要があることがわかります。 補助ノードと通常ノードは、その内部構造においても完全に異なるオブジェクトです。通常ノードにはキーと値（値）が含まれ、補助ノードはbucket'ovの始まりのマーカーとして機能します-ハッシュ値のみ。 通常のノードはリストから削除できますが、セカンダリノードは削除できません。 したがって、これら2つのタイプのノードを何らかの形で区別する必要があります。 著者は、これにハッシュ値の上位ビットを使用することを提案しています（逆ハッシュ値ではこれは下位ビットになります）：通常のノードのハッシュ値では、上位ビットは1に設定され、補助ビットでは0に設定されます：



このビットは、バケット内のキーを検索するときにリミッターの役割も果たします。バケットの境界外に到達することはありません。



上記のすべてを要約します。 キー10は2段階で挿入されます。最初に、新しい補助ノード2が親バケット0に追加されます。



次に、キー10の要素がバケット2に挿入されます。



分割順序リストは、 前の記事で検討したロックフリー順序リストに基づいているため、挿入/削除に問題はありません。 ところで、削除については、分割順序リストからの削除アルゴリズムには特殊性がありません。キーでバケットを計算し、このバケットの補助ノードで開始してロックフリーリストから削除関数を呼び出します。 補助ノードは削除されません。つまり、分割順序リストのハッシュテーブルは動的にのみ拡大できますが、縮小することはできません。



分割順序リストアルゴリズムは、ハッシュテーブルのすべての標準的な概念と矛盾するという点で興味深いものです。 モノグラフのクヌースは、適切なハッシュテーブルを作成するには、そのサイズが素数でなければならないことを証明しているため、すべての算術はモジュロ素数でなければならないことを思い出してください。 分割順序リストの場合、逆のことが当てはまります。このアルゴリズムはハッシュ値のバイナリ表現に大きく依存しており、すべての演算は2のべき乗を法としています。 このような2**N



未満の制限は、大幅な進歩にもかかわらず、整数除算ではまだ愚かである現代のプロセッサに非常によく適合しますが、シフトによる除算の置き換えが本当に好きです。



不明な疑問が1つ残っています-ハッシュテーブルの動的な拡張です。 著者は、ハッシュテーブルのセグメント化された編成を提案します。



単一の配列T[N]



代わりに、セグメントの配列Segment[M]



。これは、分割順序リストオブジェクトが初期化されるときに作成されます。 ここで、 M



は2のべき乗です。 セグメント番号は、ハッシュ値の上位ビットです。 各セグメントはテーブルT[N]



指します。これらのテーブルは、分割順序リストオブジェクトの作成時に初期化されるテーブルSegment[0]



を除き、必要に応じて動的に作成されます（バケット0は常にある必要があることに注意してください）。

このような組織では、リストオブジェクトの作成時に、セグメントM



のテーブルのサイズを計算するために要素の推定数を知る必要があります（この計算には特定のアルゴリズムはありません- Segment[]



と各T[]



両方がサイズに見合った）。 しかし、それでも、このような異常な形式ではありますが、このアルゴリズムはハッシュテーブルの成長を許可します。

まとめ

この記事では、再構築せずに、つまりハッシュテーブルを再構築せずに再ハッシュを実行できる、非常に独創的なロックフリーの分割順序リストアルゴリズムについて説明します。 このアルゴリズムは、基本的に通常のロックフリーの順序付きリストを持ち、順序付きリストのさまざまな実装をデバッグするためのポリゴンとして使用できるという点でも興味深いです。

libcdsでのこのアルゴリズムの実装は非常に良いテスト結果を示していますが、以前の記事で説明した最も単純なハッシュマップよりもやや劣っています。 これには2つの理由があります。

• これは、動的に作成されたバケットの料金です
• ハッシュ値ビットの順序を逆にすることは、プログラムで実装されている場合、依然としてかなり難しい操作です。 この手術を腺で行うことは興味深いでしょう。

アーキテクチャの観点から、このアルゴリズムを開発して、順序付きリストを分割順序リストの戦略として強調するのは非常に楽しかったです。



次の記事では、ロックフリーの順序付きリストの別の生まれ変わりについて説明します。 今回は、ハッシュマップではなく、 順序付けられたマップを作成します。