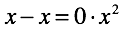パート1.実際、すべてがすでに私たちに分割されています！

パート2.真実は近くにある



最後の部分では、代数を拡張し、算術的にゼロで除算することができました。 おまけとして、この方法だけではありませんでした。 しかし、これらすべての代数は、 「内部には何があるのか​​、なぜ私たちに示されないのか」という質問には答えませんでした。



古代人は結び目を編んだが 、そのような疑問は生じなかった 。 さて、あなたがどこにいても、「何とか、0でない」。 したがって、答えは結節と現在の間にあります。 数学では、すべてが厳密で一貫しているため、答えを失うことはありません。









できる限り答えに近づけるよう努力します。 この部分は、ほぼ完全に算術の哲学に専念しています。 ほとんどの場合、資料の一部は簡単です。 しかし、私たちはここで算数の学校のコースを繰り返していません。



材料は、算術の構造を強調するように設計されています。 私たちはさまざまな側面からそれを噛み、レイヤーをはがします。 目標は、何が嘘であるかを理解することです。

2.真実は近くのどこかにある

2.1なぜわざわざ？

再び荒野に急ぐために、この質問が定期的に発生する理由と、答えを探す価値があるものを理解したいと思います。



私たちが最初に言われたときの学年を思い出してみましょう。「ゼロで割ることはできません。 「それじゃない！」 しかし、数学の前は、すべてが論理的で一貫性がありました。 スイカが積み重ねられ、メロンが差し引かれ、リンゴが転がされました。 どこからともなく、数学の研究のまさに始まりに、最初の禁断の果実が現れました。





しかし、教育システムは誰もspareしみません（ 証明 ）。 さらに進んで新しい知識を学ぶ以外に方法はありません。 「知識の飛躍」は、まるで数学の進化の千年を逃したかのように頭の中で起こります。 そして、これはほんの始まりに過ぎません。

「 ...過度の急ぎを示す必要はありません 。 認知行為の結果として彼に起こる内なる革命に慣れる時間を学生に与える必要があります 」 -F .クライン、「高等教育の観点からの初等数学」

高校では、円と三角形の式、判別式、三角関数のアイデンティティなどがどこからともなく現れます。 それらを結合するものは何ですか？ それらのすべては上から来た、それはどこで完全に不明です。 あなたはそれらを使用する必要があり、最悪の場合、記憶します。



大学に入学すると、大半は、行方不明の資料に戻る代わりに、専門性に偏った「塔」を研究します。 上から来た数式の量はもう気にしません。



はい、教育システムは理解できます。 スペシャリストは、出展者が計算のどこから来たかを知っているという事実ではなく、結果に対して支払われます。



その結果、数学者のように結論に達しません。 「知識の飛躍」の瞬間、つまり論理的連鎖の一部を落とすと、聖sa式が行われます。 私たちは彼らが私たちに語ったことを信じます。 教科書は経典に変わります！









ゼロによる除算の禁止は、数学の最初で最も邪魔な禁止です。 したがって、それは一生記憶されます。 これは、「暗闇に覆われた謎」のように、すべての数学にその痕跡を残す教育学的問題でもあります。 これと比較して、これは複雑な問題であり、欠落している論理チェーンの大部分を見つけることは難しくありません。



聖文を教科書に戻すことができます。 禁止の理由は厳密に定義する必要があります。 それを明確に提示する教育者の仕事。 科学は疑いをsoくべきではありません。

2.2除算とは

キャプテンエビデンスは、ゼロで除算するためには、除算とは何であるかを知る必要があると述べています。 悲しいことに、Googleは「ゼロによる除算の魔法」の支持者の多くは、この地獄の最初の円さえも通過しないことを示唆しています。 つまり、彼らが何をし、何をするのかを理解することです。 ウィキペディアを見てみましょう：

除算（除算）は、4つの最も単純な算術演算の1つであり、乗算の反対です。 除算は、あるものが別のものに含まれる回数をカウントする操作です。

これから何が続きます：

• 除算は独立した操作ではありません。 乗算によって決定されます。 乗算の定義を見ると、加算によって決定されます。 減算も加算により定義されます。 独立して追加し、誰にも依存しません。
  
  
  
  
• 定義にはゼロに関する言及はありません。 ゼロによる除算が広く禁止されているため、これは非常に奇妙です。 ところで、他の算術演算の定義にはゼロについての言及はありません。
  
  
  
  
• 定義の2番目の部分は定義の一部ではなく、単なる説明です。 他の実績のあるソースのアナログと比較することで確認できます 。
  
  

ここで見つけた最も有用なものは、オペレーション間の接続であるようです。 除算は3番目の抽出、乗算と減算-2番目の加算、1番目の加算-のワインであると言えます。 おそらくこの理由で、ゼロで作業しているときに部門が失敗し始めました。

2.3生成操作

したがって、 加算演算のみに、2つの初期引数（項）から演算の結果（合計）を決定する方法に関するルールが含まれています。 他のすべての算術演算は、このルール（一致する数値）を使用しますが、さらに「追加条件」を課します。









「追加条件」に応じて、算術演算は直接および逆に分割できます。

1. 直接操作：これは加算、乗算、累乗です。 追加によってこれらの操作を表現すると、すべての用語が既知のままになります。 いずれかの操作の結果を判断することは難しくありません。
   
   
   
   
   
   
   
   
   
   
   
   
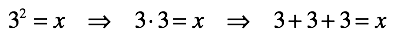
2. 逆演算：減算、除算、ルートの取得（対数）。 これらの操作は、対応する直接操作を基本とし、それを「反転」します。 したがって、加算によって演算を表現する場合、少なくとも1つの用語は不明です。 この用語は、操作の結果です。 量は通常知られています。
   
   
   
   
   
   
   
   
   
   
   
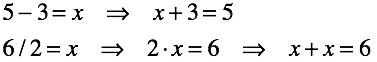
   一般的な場合、操作の結果を決定することは簡単な作業ではありません。
   
   
   
   
   
   
   
   
   
   

すべての直接操作には1つのプロパティがあります。 彼らは閉じています。 つまり、結果のタイプは入力数のタイプによって完全に決定されます（2つの整数の積から小数の結果を取得することは不可能です）。



逆演算は部分的にしか閉じられていません（整数の根の値は整数である場合とそうでない場合があります）。 結果を選択できない場合、操作は定義されません 。 この問題は長い間、簡単な方法で解決されています。操作と数値の結果の記録を新しいタイプの数値と考えてください。 。



したがって、逆演算と新しいタイプの数値を「生成」すると言えます。



数学言語：

一般的な場合、「逆演算」という用語の使用は、演算が新しいタイプの数値を生成する能力を示すために受け入れられません。 たとえば、「追加条件」は次のことができます。

• 操作の結果を1つ以上の用語で記述します（上記の例に示すように）。
• 操作に参加した用語の数（小数、ルートを使用した無理数）の質問に対する答えとして、操作の結果を決定します。
• 無限数の項の合計として演算の結果を決定します。 さらに、すべての用語が知られています（Pi番号とオイラー番号）。

除算は生成操作の1つです。 おそらく、出生過程で何かがおかしくなり、新生児が負傷しました。 この質問に答えるには、部門がどこから来たのか、ゼロがどこから来たのかを理解する必要があります。

2.4算術の進化

算術演算のアイデアと、それによって生成される数値のタイプを構造化してみましょう。 わかりやすくするために、算術の進化がどのように進むかを示すオプションの1つを示します。

2.4.1範囲

私たちは洞窟の中にいます。 数える能力があれば、誰も生まれませんでした。 しかし、「熟考」の過程で、「量」の概念が何であるかについて理解が生まれました。 つまり、2つのマンモスと2つのリンゴには共通点があり、指を曲げることでそれを表現できることがわかっています。 したがって、この段階では自然数しか知りません。









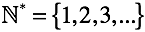
多くの自然数には、明確にするためにアスタリスク「*」が付いています。 以下、「ゼロ」の概念がないことを強調します。



自然数のシーケンスにはいくつかの正式な定義があります。 私たちは、 ペアノの公理を基礎としています。 これらの定義が古代人によって記述されなかったことは注目に値します。 それらは19世紀にのみ登場し、その後改良手順を経ました（最初のバージョンでは9でしたが、現在の形式ではすでに5があります）。



私たちのタスクの枠組みにおける正式な定義とその本質を考慮してください（伝統的な言葉による説明はWikipediaにあります ）：

1. 
   
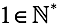
   「1」という数字があり、それは当然です。
   
   
   
   
2. 
   
   フォローアップ関数 S（x）が導入されました。 すべての自然引数について、次の自然数を返します。 最初の近似（非常に大まかな）では、これはS（x）= x + 1、たとえば2 = S（1）および3 = S（S（1））です。
   
   
   
   
3. 
   
   生成された番号のシーケンスのグローバルループバックに対する明示的な禁止が導入されました。 数値を生成することで、生成を開始した要素、つまり1つを取得できません。
   
   
   
   
4. 
   
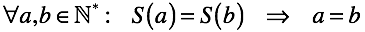
   follow関数の引数が異なると、結果も異なります。 したがって、ローカルループの明示的な禁止が導入されています。 つまり、follow関数は、既に生成された数値を再生成するべきではありません。
   
   
   
   
5. 
   
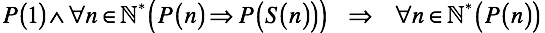
   数学的帰納法により、シーケンス要素のレベルからシーケンス全体のレベルまで上昇させることができます。 ある文 「P」が単一性および隣接する要素の各ペアに当てはまる場合、シーケンスのすべての要素に当てはまります。
   
   
   
   たとえば。 数字2と3の場合、それらの間に1つの中間要素2.5があり、3と4の場合は3.5であるなどです。 隣接する自然数の間には中間要素があり、それが唯一の要素であると結論付けます。

これらの公理からどのような結論を引き出すことができますか？ 任意の形式（グローバルまたはローカル）での呼び出しの禁止が導入されています。 呼び出し音の禁止には、常に次の要素の存在が必要です。 したがって、「量」の概念に基づいて、 「無限」の数学的概念が表示されます。 「無限」の概念は、「量」の概念なしでは存在できません。



数学言語：

ピアノの公理の「開始要素」はほとんどゼロです。 これを実行できない理由は、操作「減算」の説明で開示されます（すぐに）。



follow関数は、単語の文字通りの意味で加算演算を使用しません。 これは、自然数のセットを構築し、加算演算を正式に定義するために使用される基本的な関数です。



つまり、数値と算術演算の両方が、follow関数を使用して決定されます。



フォローアップ関数は、アルゴリズムの理論で考慮されるプリミティブな再帰関数のクラスに属します 。 ご存知のように、 再帰の概念には、その有限性（ 終端分岐の到達可能性）の要件は含まれていません。つまり、「無限」の概念も暗黙的に定義しています。

2.4.2追加

私たちの進化の中で起きた最初の作戦。 指全体のように曲げないでください、結果は全体になります。 リーダーの指の合計が他のすべての指よりわずかに大きい場合を除きます。 十分な指がない場合は、いつでも洞窟内の科学助手を呼び出して、放電グリッドを拡大できます。

2.4.2減算

木曜日に、ハンターは12匹のマンモスを撃ちました。 金曜日に5個食べました。 マンモスは何匹残っていますか？











この問題は、指の延長を導入することで十分に解決されます。 しかし、このアプローチは常に機能するとは限りません。 たとえば、週末の埋蔵量を見積もるために、ハンターは残りの部分で7本の指を曲げ、土曜日（1日あたりの消費率）で5本の指を伸ばし、日曜日にそれを開くように「試行」します。











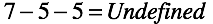
この時点で、「try」と「catch」の間に「ArithmeticException」が発生します。 結果は定義されていません 。 私たちの操作は、減少が控除額よりも大きい場合にのみ定義されます。









ただし、減算の定義には制限がありません。 要件「a> b」を取り除くために、 「順列規則」を導入します。 つまり、デクリメントされ減算されたものを交換しましょう。 ただし、IDがtrueのままであるためには、マイナス記号などのマーカーで結果をマークする必要があります。 数学のすべての種類のマーカーは一般的です（たとえば、 ）











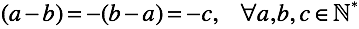
「順列」の補助演算により、最初の抽象化-「 負の数 」に到達しました 。 自然数のマイナス記号の形のマークは、遅延減算の記号にすぎません（ただし、これはこれまでのところです）。









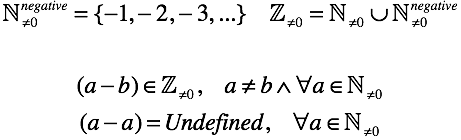
減少と減算が等しい場合、未定義のケースは1つだけです。 定義したい場合は、「何もない」という概念とは何かという質問に答える必要があります。 これらすべての難しさを理由に、記号「0」で「なし」を示します（後で詳しく調べます）。









「ゼロを追加/削除するためのルール」の形で決定を修正することは残っています。 それらは、いくつかの単純な順列の後のゼロの定義から続きます。









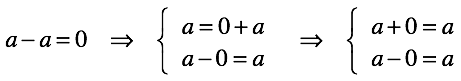
導入されたルールがどの程度機能するかを見てみましょう。 方程式を解くと、2つの既知の数値から常に未知の3分の1を見つけることができます。 方程式のどの部分にあるかは問題ではなく、解は常に一意です。









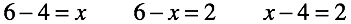
順列の結果として負の数が表示されましたが、ゼロは「無」を埋めました。 負の数とゼロはさまざまな方法で生まれます。 さらに、進化の2つの分岐を検討します。ゼロのないすべての数字とゼロの別々の数字です。

2.4.3乗算

乗算は定義上、加算の省略表記です。 自然数を掛けると、結果は自然になります。 進化のこの段階で、定義の有用性は終わります。









定義の負の数については、それらを掛ける方法についての言葉はありません。 これらの規則は適用された問題を解決する過程で徐々に形成されました 。 現代の解釈では、それらは「記号の規則」の形での乗算への追加として知られています。 それらは非常によく定義されているので、それらをゼロ以外の整数に適用すると、操作は閉じたままになります。









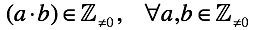
ゼロの場合、状況は根本的に異なります。 別のルール、「ゼロを乗算するルール」が導入されます（任意の数にゼロを乗算するとゼロになります）。 しかし、この規則は新しいように思えます。 他のルールを導入することはできません。 乗算の定義は、加算と厳密に関連しています。 加算を介して乗算を開き、「ゼロの加算/減算のルール」をそれぞれ使用します。ゼロ以外は何も取得できません。









数学言語：

算術代数と一般代数の加算と乗算の操作を比較すると、1つの重大な違いに気付くことができます。 算術では、これらの操作は定義により関連付けられます。 分配法はこれらの定義の結果です。 一般的な代数では、逆に、操作は互いに独立して記述され、すでにフィールドの定義（より正確にはリング）で定義されており、分布法則によって接続されています。 その結果：

• フィールド定義では、逆要素の要件があります。 さらに、乗算と加算については、要件は対称的に説明されていません。 ニュートラル加算要素に逆乗算要素が存在しないことは許可されていますが、逆はできません。
  
  
• 車輪の記述に対称性を持たせるために、私は通常の分布法則を放棄しなければならず、したがってフィールドを操作することはできませんでした。

普遍性の冠である「耳の後ろ」のフィールドは、初等算術に引き寄せられます。 しかし、このサポートを取り除くために（操作の要件を対称的に記述するために）分布法の定義を拡張する必要があります（もちろんリングから開始）。 別の代数システムが普遍性の冠になる可能性があると信じる理由があり、その分野は特別なケースであることが判明します。

2.4.4部門

除算は乗算の逆です。 正の数と負の数を持つ方程式では、複数の数を置き換えることが可能になります。









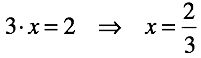
その結果、操作は「有理数」を生成します。









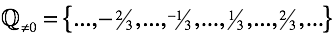
それらを算術に入力するために、セットには「通常の分数を使用した演算の規則」が含まれています 。 幸いなことに、これらの規則は、以前に紹介した「署名規則」と共存します。 その結果、方程式は、任意の配置に対して2つの既知の数によって未知数を決定する機能を保持します。









ゼロの場合、有理数で乗算できます。 以上で、調和は終わりました！ 任意の数を持つ3種類の方程式のうち2つだけが解を見つけることができます。















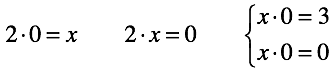
第一に、解答が見つからないほど不快な数の方程式を作成することが可能になりました。 解決策は「不可能」です。









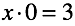
第二に、無限の数の解がある方程式を作ることが可能になりました。 それらのいずれかを選択することもできません。 決定は「曖昧」です。









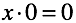
推測するのは簡単です。ゼロによる除算の問題の根源は、ゼロの乗算の「不可能性」と「あいまいさ」にあります。 乗算は、「ゼロの加算/減算のルール」を順に伝えます。 実際、加算のみを使用して、同じプロパティを持つ方程式を指定できます。









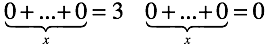
両方の式で、任意の数またはゼロを取得するために追加する必要があるゼロの数を決定する必要があります。

部門は質的に新しいものをもたらしませんでした。 具体的なエンティティへの加算の「不可能性」と「曖昧さ」が 、それぞれ1/0と0/0の形式の不確実性で変化しました。









最初の容疑者としての除算は、ゼロで除算することが不可能であるという事実のせいではないことがわかります。









「ゼロ」の概念が存在しない限り、累乗および根の取得（対数）を含むすべての演算は十分に閉じられ（真理は複素数に基づく）、算術はうまく機能します。 しかし、1つの「しかし」があります。そのような算術の構成では、減算演算は完全には決定されません。



ゼロを導入すると、加算と減算がうまく機能します。 他の操作では、松葉杖をインストールする可能性が高くなります（ ）等しい数ではなく。

2.5ゼロとは何ですか？

したがって、除算操作はゼロによる除算の禁止のせいではありませんでした。 ゼロについて知っていることすべてをまとめてみましょう。

1. ゼロの必要性は、減算演算の決定に現れました。
   
   
   
   
2. 減算の不確実性のほとんどを解決するために、「順列規則」が導入されました。 数字の前のマイナス記号は、実際には「遅延減算」マーカーです。 「順列規則」がマスターしなかったすべては、ゼロを閉じました。 本質的に、 ゼロは「無」の概念を示すために導入されました 。
   
   記事の前の部分（数直線の射影拡張）で、「天井から」符号なしの無限大を導入しました。 ゼロ、私たちが理解していないすべてのものに対する同様の「ギャグ」。 結果は、新しい不確実性の形で、非常に予測可能です。
   
   
   
   
3. 「無」の概念は、「数量」の概念 （自然数と加算を決定するための基礎）とは関係ありません 。 これらの概念は単独で存在し、たとえば「5つのリンゴ」や「真空」など、完全に独立して「熟考」できます。 つまり、「無」の概念は「数量」の概念とは関係がないため、本質的にゼロも自然数とは関係ありません。 減算はこの概念を使用しますが、それを引き起こしません。
   
   
   
   結果の演算が存在しないため、ゼロは他のすべての数値と定性的に区別されます。
   
   
   
   私たちが考慮していない数字の種類と操作の関係を明確にするために、可能な限り簡潔に進化のテーマを続けます。 私たちは部門に落ち着きました。 複素数と無理数の一部は、負の数の根（対数）をとる操作によって生成されます。 他の非合理的なもの（Pi数とオイラー数）は、 無限の和と無限の乗算の導入により表示されます。 . , .
   
   
   
   
4. - “” “” “” . .
   
   
   
   
5. , . , , “ / ” . , , . , .
   
   
   
   
   
   
   
   

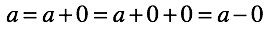
最後の段階で、詳細に停止する価値があります。絶対ゼロではないことを想像してみましょう。



マンモスがあるとしましょう。輸送にはコンテナが必要です。マンモスをコンテナに入れて引き抜くと、コンテナは「何もない」状態になります（上の写真と同じように）。ただし、2つのマンモスのパッケージは1つのマンモスのパッケージとは多少異なります。盗難の場合、残りのパッケージのサイズに応じて請求する理由があります。そのため、ある「何もない」から別の「何もない」という不一致が生じる場合があります。









「何もない」が違うのか、「何もない」が単一の絶対的な本質なのか？これは答えられない質問です。神が存在するかどうかについての議論も同様であり、無意味です。この世界での答えはわかりません。



数学言語：

:

1. . , . , . , :
   
   
   
   
   
   
   
   
   
   
   
   
2. . . , , . ( ) :
   
   
   1. 
   2. 
   3. 
   4. 
   . . .
   
   . .
   
   
   
   
3. アルゴリズムの理論。算術をさらに詳しく調べることができます。自然数のシーケンスを構築し、加算演算を決定するために、プリミティブな再帰関数のクラスが使用されます。シーケンス関数 S（x）は、ペアノの公理（その1つ）で使用されます。それとともに、ゼロ関数 O（x）が定義されます。これは常にゼロを返す関数です。

したがって、自然数も加算も（したがって他の演算も）行われない算術演算の最下部にはゼロがあります。









まあ、算術はゼロがいくつあるべきかという質問に答えることができません。 1つのゼロを使用します。前半で説明したホイールでは、無限の数のゼロを使用した算術が使用されました。しかし、ゼロの有限数がありますが、複数あります。



たぶん、そのような算術はうまく使われています。JavaScriptで実装された「符号付きゼロ」による算術の最も明るい例の1つ。



数学言語：

符号ゼロは、+ 0および-0と同じ方法で記述されますが、infinitesimalの計算とは何の関係もありません。



符号付きゼロの導入は、番号行を拡張するための別のオプションです。では、一般的なトポロジ非常に近い（同一ではない）スペース「がある2つの原則に沿って（ないハウスドルフ）」。

しかし、この算術でさえ不確実性を伴います。





ゼロの数が有限である限り、算術の不確実性は残ると結論付けることができます。



概して、ゼロの扱い方に関係ありません。 単一の絶対零度が必要な場合でも、数個または無限の場合でも、算術は常に私たちに適応できます。

2.6無限は私たちのすべてです

最後に、無限の数のゼロを含む数値軸の少なくとも1つのバージョンを提示したいと思います（この例では概念を説明し、数学的厳密性を主張しません）。



減算では、減分と減算が等しい場合、ゼロを入力する代わりに、「削減」の操作を定義します。 つまり、反対の符号を持つ同等の式を削除できます。 しかし、すべてを削減した場合、結果は今後の使用に適さなくなります。









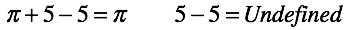
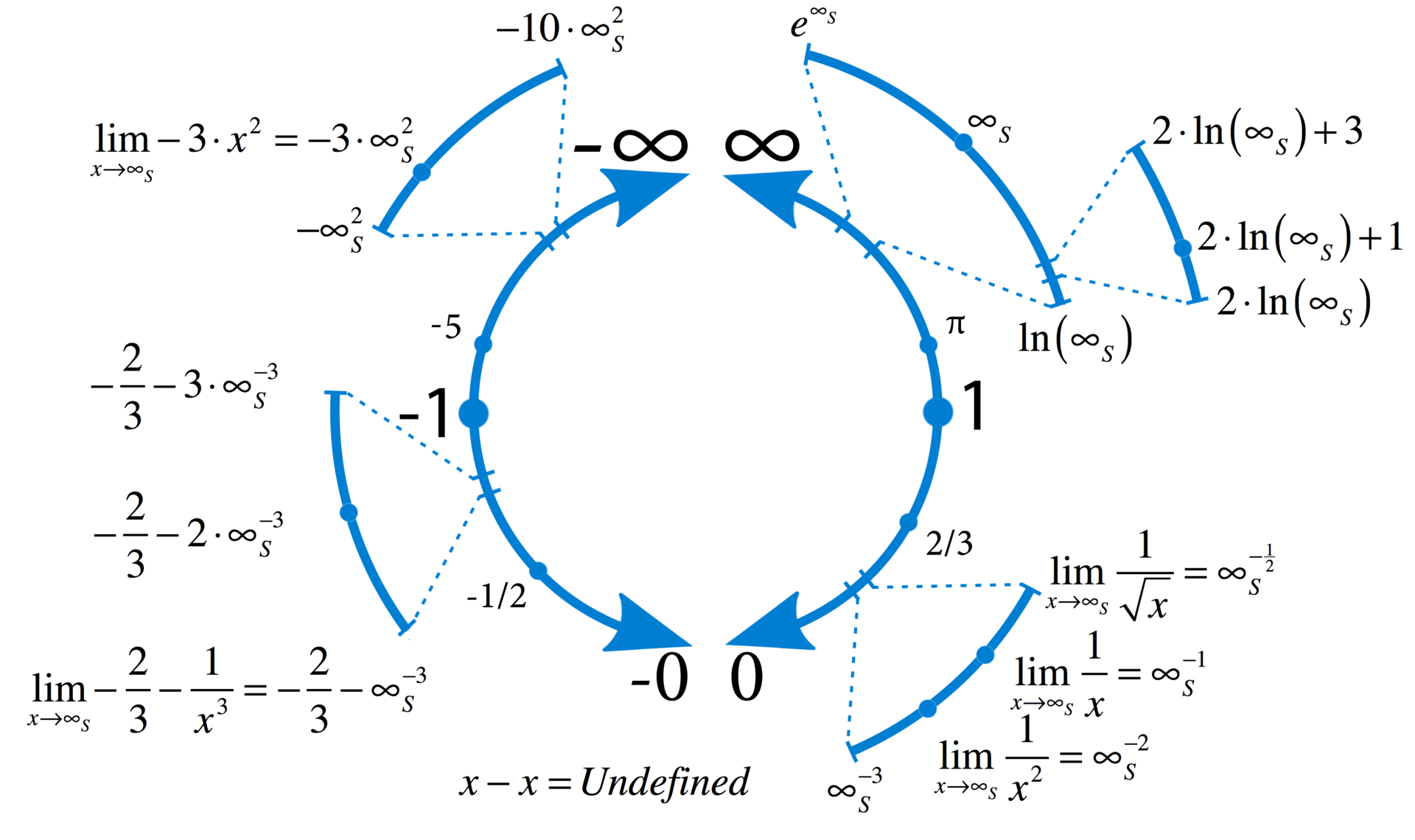
数値軸のカウントダウンは、（「量」の元々の概念の最初の数から）単一で始まります。 残りの数値を生成するために、シーケンス関数で定義された無限シーケンスを使用します （ ペアノの公理でも使用されます）。 これが無限シーケンス参照ジェネレーターになります。



follow関数を使用して非常に小さな数を取得するには、非常に大きな数を生成するのと同じくらいの労力を費やす必要があります。 関数f（x）= 1 / xおよびf（x）= xを使用します。 有理数の小数化はタスクではないため、関数の計算の複雑さは同じです。



「絶対ゼロ」（記号ゼロでマーク）も「潜在的無限大」 （符号なし無限のシンボルでマーク）も達成できないため、軸は両方向に無限にユニティから成長します（スケールは不均一です）。









減算を決定する際に、「順列規則」が定義されます。 次に、ラインのコピーを作成し、ミラーに表示します。 双子の数字と到達不可能な制限にはマイナス記号が付いています。 正の線は負の線と接続されていません。 ある直線から別の直線への移行は、「順列規則」によってのみ実行されます。









明確にするために、結果の数値線を円の形で示します。 射影拡張で行ったように。 ただし、制限値は閉じません（コンパクト化は実行しません）。 この変換はセマンティックロードを実行せず、知覚を改善するためにのみ実行されます。









これで最も重要なことの準備ができました。 単一の潜在的な無限から実際の無限の無限のセットへの移行を行います（ 非標準分析で同様のアプローチが使用されます ）。



無限大の量を完全な数と呼びます。 実際の無限大を参照するために、フォロー関数が任意の数に達する「速度」を取ります。 この番号を示します 。 潜在的な無限大と混同しないでください 彼女はまだ達成できません。



さまざまな実際の無限大を取得するために、数値に傾向があるときに関数の制限の概念を使用します 。 古典的な分析で慣習的であるように、無限小数（低次）を破棄せず、無限大の定数を吸収しません。 番号を構成するすべての情報を保持します。 したがって、無限に大きい数を比較する機会があります。









番号を上げる 負の程度まで、無限の数を取得します。 実際、これは無限のゼロの数であり、互いに比較することができ、算術で使用できます（従来の分析では無限小の値ではありません）。



数学言語：

一般代数の観点からは、ゼロ（中立要素）がないため、代数システムは体ではありません。 非標準分析は、同様の実際の無限大で動作し、それらはハイパーリアル数と呼ばれます 。 ゼロ（中立要素）は、超実数の1つです。 したがって、非標準分析の代数システムはフィールドで動作します。



参照無限 非標準分析の数の1つを表します。 ただし、非標準分析では、単純化された「速度」の概念の代わりに、数値は無限シーケンスの等価クラスです。 私たちの概念では、すべての代数演算は次の関数で表現できるため、算術的に形成された実際の無限大は次の関数で表現できることを意味します。 。



実際、私たちが慣れている形で、制限は実際には単純化されなくなります。 ここで、変数を 。 ロテルの規則も適用されません。 最初の部分では、古典では、導関数を決定するときに、極小値が破棄されることが示されました。 ただし、非標準分析の限界の概念はまだ存在しますが、ある程度広く定義されていることに注意してください。

実際的な必要性が生じた場合、（上記で定義した「削減」の代わりに）等しい数の減算演算を決定することが可能です。 たとえば、元の番号よりも小さい番号である場合があります （ ホイールからの方程式のアナログ）。 算術は閉じられます。 ただし、2つの2の合計はすぐにテール付きの4に等しくなることに注意する必要があります。 これは相対性理論における速度の追加に幾分似ています。 別の例は、熱力学と絶対零度温度の概念です。 分子を停止することにより、原子は動き続けます。 原子を止めても、クォークはまだ動いているなど。 浸漬は無限です。

エピローグ

私たちは過去と未来の間、ミクロとマクロの世界の間にいます。 すべての分野で、遅かれ早かれ、限界を超えて、それを超えることはできなくなります。これは正常なことです。



数学では、そうではありません。 ゼロは数字だと言われています。 それから、他のすべての数字と同等に置きます。 次に、マイナス1から1までのパスの長さは2であることが通知されます。 そしてこの瞬間、私たちの意識は最終的に残りの数字の中からゼロを解消します。



ゼロで割り切れないのは、かつて「何もない」という概念と「量」という概念を混ぜていたことを忘れていたからです。